AtCoder Beginner Contest 330 题解
目录
- A - Counting Passes
- B - Minimize Abs 1
- C - Minimize Abs 2
- D - Counting Ls
- E - Mex and Update
A - Counting Passes
原题链接
题目描述
给定N个数和一个整数L,输出大于等于L的数的个数。
public static void solve() throws IOException{int n = readInt(), m = readInt();int cnt = 0;for (int i = 1; i <= n; i++) {int a = readInt();if (a >= m) cnt++;}printWriter.println(cnt);
}
B - Minimize Abs 1
原题链接
题目描述
给定一个含有n个元素数组arr,和两个整数L和R,对于每个整数 a r r [ i ] arr[i] arr[i]求出一个数 X ( L ≤ X ≤ R ) X(L \leq X \leq R) X(L≤X≤R),使得对于任意的 L ≤ Y ≤ R L \leq Y \leq R L≤Y≤R 都满足 ∣ X − a r r [ i ] ∣ ≤ ∣ Y − a r r [ i ] ∣ | X - arr[i]| \leq | Y - arr[i] | ∣X−arr[i]∣≤∣Y−arr[i]∣。
思路:分类讨论
- 分别讨论 a r r [ i ] arr[i] arr[i]与 L L L和 R R R的大小即可。
public static void solve() throws IOException {int n = readInt(), l = readInt(), r = readInt();List<Integer> list = new ArrayList<>();for (int i = 1; i <= n; i++) {int a = readInt();if (a <= l) {list.add(l);} else if (a >= l && a <= r) {list.add(a);} else {list.add(r);}}for (int p : list) {printWriter.print(p + " ");}
}
C - Minimize Abs 2
原题链接
题目描述
给你一个整数 D ( 1 ≤ D ≤ 2 × 1 0 12 ) D(1\leq D \leq 2\times 10^{12}) D(1≤D≤2×1012),求出非负整数 x x x 和 y y y 的最小值 ∣ x 2 + y 2 − D ∣ |x^2+y^2-D| ∣x2+y2−D∣。
思路:二分
- 先确认 x 2 x^2 x2,再二分枚举出 y 2 y^2 y2即可,但是要分类讨论一下,即 ① x 2 + y 2 ≥ D x^2+y^2 \geq D x2+y2≥D ② x 2 + y 2 ≤ D x^2+y^2 \leq D x2+y2≤D。
public static void solve() throws IOException{int N = 2000000;long[] s = new long[N];for (int i = 0; i <= N - 1; i++) {s[i] = (long) Math.pow(i, 2);}long d = readLong();long res = Long.MAX_VALUE;for (int i = 0; i < N; i++) {int l = -1, r = N;while (l + 1 < r) {int mid = (l + r) >> 1;if (s[i] + s[mid] >= d) {r = mid;} else {l = mid;}}res = Math.min(res, s[i] + s[r] - d);}for (int i = 0; i < N; i++) {int l = -1, r = N;while (l + 1 < r) {int mid = (l + r) >> 1;if (s[i] + s[mid] <= d) {l = mid;} else {r = mid;}}if (l != -1) {res = Math.min(res, (d - (s[i] + s[l])));}}printWriter.println(res);
}
D - Counting Ls
原题链接
题目描述
给定一个 N × N N \times N N×N 的仅包含o和x的二维字符矩阵,你需要求出能满足以下条件的字符三元组的个数。
- 该三元组上的字符在矩阵中的位置各不相同,但是都是
o。- 该三元组中,其中两个字符在同一行,其中两个字符在同一列。
思路:计数
- 如果二维矩阵的一个位置的字符为
o时,该字符贡献为 ( r o w [ i ] − 1 ) ∗ ( c o l [ j ] − 1 ) (row[i] - 1) * (col[j] - 1) (row[i]−1)∗(col[j]−1),其中 r o w [ i ] row[i] row[i]表示该行o的个数, c o l [ i ] col[i] col[i]表示该列o的个数。
public static void solve() throws IOException{int n = readInt();String[] strings = new String[n + 1];for (int i = 1; i <= n; i++) {strings[i] = (" " + readString());}int[] row = new int[n + 1], col = new int[n + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (strings[i].charAt(j) == 'o') {row[i]++; col[j]++;}}}long res = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (strings[i].charAt(j) == 'o') {res += 1l * (row[i] - 1) * (col[j] - 1);}}}printWriter.println(res);
}
E - Mex and Update
原题链接
题目描述
给定一个长度为 n n n的整数序列A,你需要进行Q次操作,第 i i i次操作由二元组 ( p , x ) (p,x) (p,x)组成,即先将 A [ p ] A[p] A[p]修改为x,然后求出序列A的 m e x mex mex并输出。
思路:技巧
- 首先 m e x mex mex一定是 0 ∼ n 0 \sim n 0∼n 中的数!所以我们只需要统计出 0 ∼ n 0 \sim n 0∼n中每个数字在序列
A中出现的次数和哪些数字从没出现过。- 对于每一次操作,在修改 A [ p ] A[p] A[p]值的前后,分别对新旧 A [ p ] A[p] A[p]出现的次数进行修改,① 如果旧 A [ p ] A[p] A[p]在修改出现次数后变为
0,则要重新添加至集合; ② 如果新 A [ p ] A[p] A[p]修改出现次数前是0,则要将其从集合中删除。
public static void solve() throws IOException {int n = readInt(), q = readInt();int[] a = new int[n], c = new int[n + 1];for (int i = 0; i < n; i++) {a[i] = readInt();if (a[i] <= n) {c[a[i]]++;}}TreeSet<Integer> set = new TreeSet<>();// 统计没有出现过的数字for (int i = 0; i <= n; i++) {if (c[i] == 0) set.add(i);}for (int i = 0; i < q; i++) {int p = readInt() - 1, x = readInt();if (a[p] <= n) {c[a[p]]--;if (c[a[p]] == 0) {// 原先的a[p]出现的次数减一后,出现次数变为0,就添加至 set集合set.add(a[p]);}}a[p] = x;if (a[p] <= n) {if (c[a[p]] == 0) {// 现在的a[p]原先不在set集合中,现在要移出,因为出现次数不为 0了set.remove(a[p]);}c[a[p]]++;}printWriter.println(set.first());}
}
相关文章:

AtCoder Beginner Contest 330 题解
目录 A - Counting PassesB - Minimize Abs 1C - Minimize Abs 2D - Counting LsE - Mex and Update A - Counting Passes 原题链接 题目描述 给定N个数和一个整数L,输出大于等于L的数的个数。 public static void solve() throws IOException{int n readInt(), m…...

论文速读《DeepFusion: Lidar-Camera Deep Fusion for Multi-Modal 3D Object Detection》
概括主要内容 文章《DeepFusion: Lidar-Camera Deep Fusion for Multi-Modal 3D Object Detection》提出了两种创新技术,以改善多模态3D检测模型的性能,通过更有效地融合相机和激光雷达传感器数据来提高对象检测的准确性,尤其是在行人检测方面…...
)
关于前端处理后端轮询的操作 (总结)
使用场景:前端首次发起请求获取数据,若失败则每隔1s发起一次知道成功获取数据为止解决方案: 使用轮询操作,涉及定时器的使用和关闭 (使用vue2代码为例) data() {return {pollingResult_en: null, // 处理轮询结果bizI…...
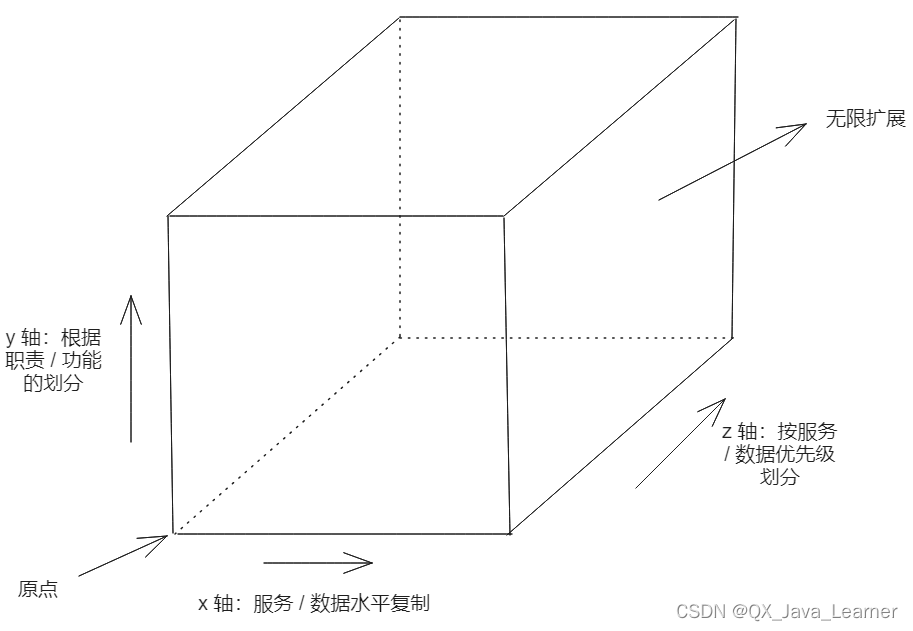
【SpringCloud】设计原则之单一职责与服务拆分
一、设计原则之单一职责 设计原则很重要的一点就是简单,单一职责也就是所谓的专人干专事 一个单元(一个类、函数或微服务)应该有且只有一个职责 无论如何,一个微服务不应该包含多于一个的职责 职责单一的后果之一就是职责单…...

UDP分片和丢包与TCP效果对比
UDP 分片 与 丢包,UDP 真的比 TCP 高效吗? UDP(用户数据报协议)和TCP(传输控制协议)在很多方面都有显著的区别。总体来说,TCP更适合需要可靠传输的应用,例如网页浏览、电子邮件等&a…...
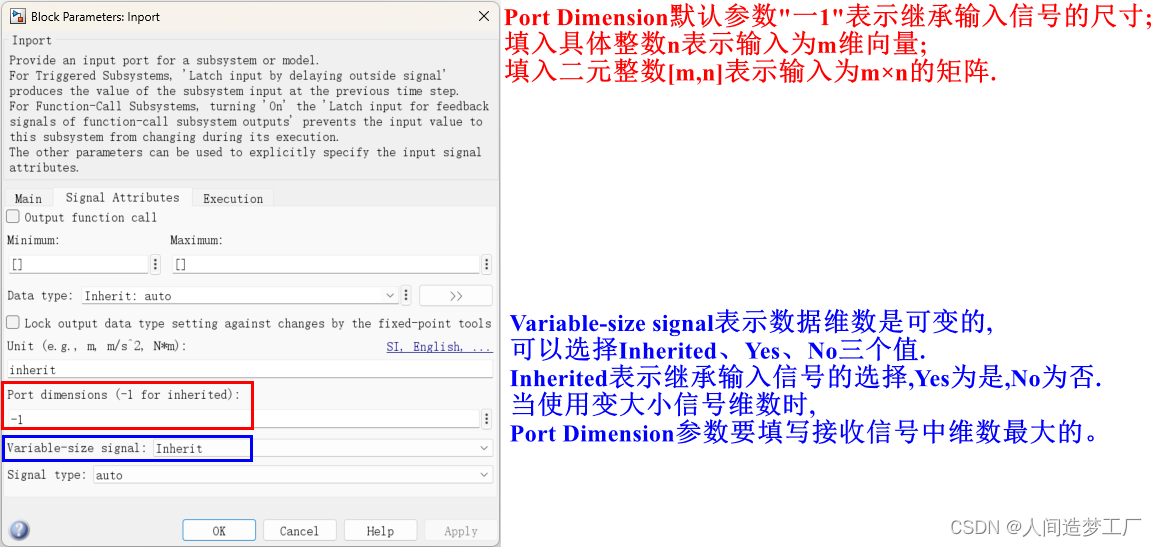
Inport 模块
文章目录 Interpolate datainport 模块存在于模型最顶层Port Dimension 和 Variable-size signal Interpolate data Interpolate data:当将 Workspace 的数据导人模型时, 对没有对应数据点的采样时刻进行线性插值的开关选项。 inport 模块存在于模型最顶层 inpo…...
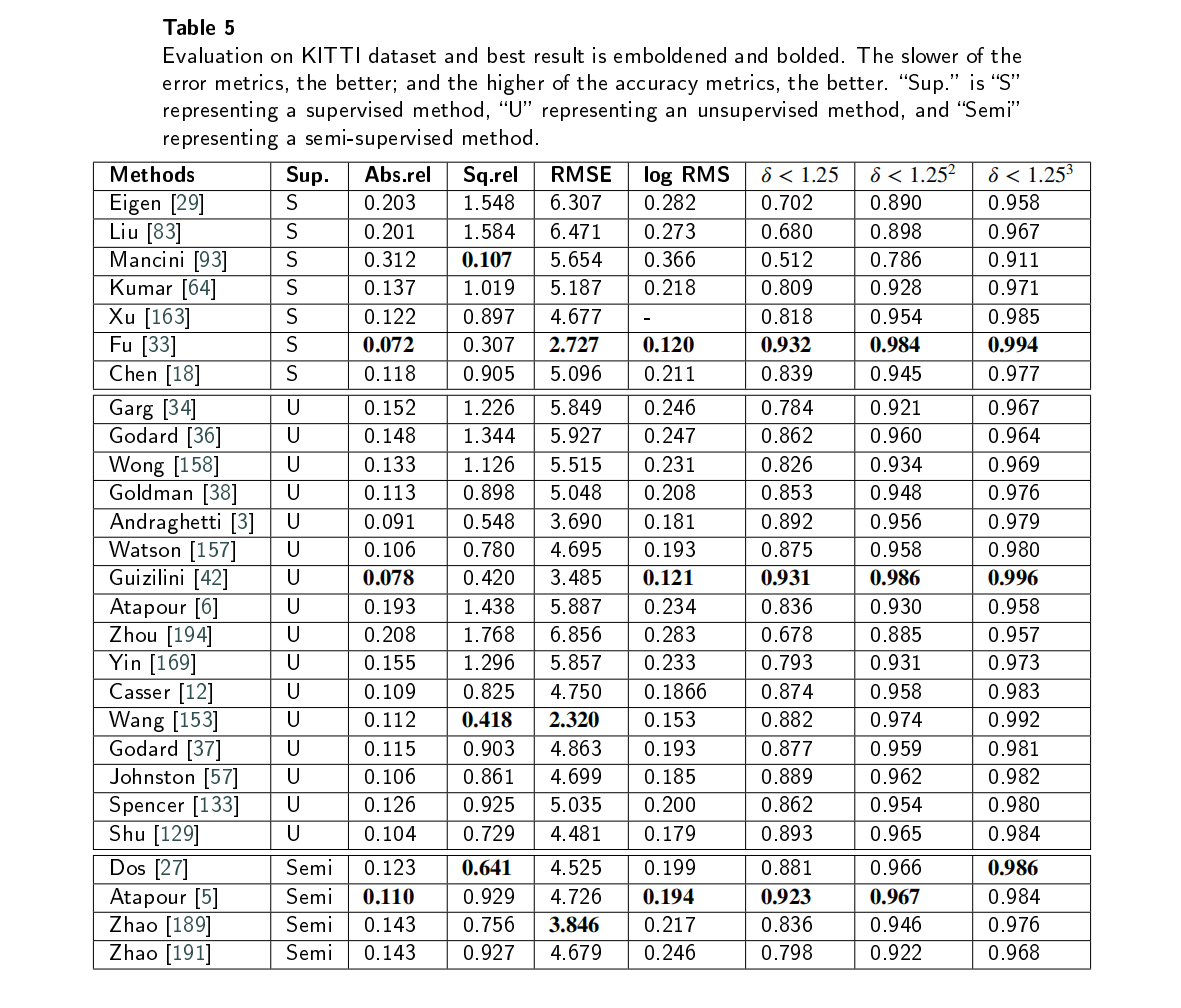
Deep Learning for Monocular Depth Estimation: A Review.基于深度学习的深度估计
传统的深度估计方法通常是使用双目相机,计算两个2D图像的视差,然后通过立体匹配和三角剖分得到深度图。然而,双目深度估计方法至少需要两个固定的摄像机,当场景的纹理较少或者没有纹理的时候,很难从图像中捕捉足够的特…...
)
点云从入门到精通技术详解100篇-基于深度学习的稀疏点云障碍物检测(续)
目录 3.1 连续帧点云空间特征融合 3.1.1 点云预处理 3.1.2 地面分割 3.1.3 自适应点云聚类...
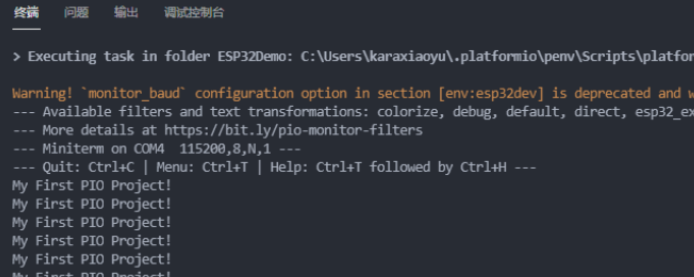
使用VSCode+PlatformIO搭建ESP32开发环境
Arduino IDE本来就是为创客们开发的,虽然没代码提示功能,文件的关系也不清晰,函数不能跳转,头文件也打不开,但人家的初衷就是为了简单而生的;但还是有一些同学喜欢高级点的IDE,也没问题…...

使用flask返回json格式的数据
Flask Flask是一个使用Python编写的轻量级Web框架,它的设计理念是保持简单、灵活和易扩展。它的核心是Werkzeug和Jinja2,并且它本身只提供了非常基础的Web框架功能,例如路由和请求处理等。 使用Flask可以快速创建一个Web应用程序,…...

如何排查java 内存溢出OutOfMemoryError?
当使用Spring Boot进行文件上传时,文件会被读取到内存中进行处理。如果上传的文件较大,会占用大量的内存空间,从而导致内存溢出(OutOfMemory)问题。以下是一些建议的排查方案: 调整 JVM 内存设置ÿ…...

Prometheus环境搭建和认识
Prometheus 环境搭建 1.prometheus 简介 Prometheus是基于go语言开发的一套开源的监控、报警和时间序列数据库的组合,是由SoundCloud公司开发的开源监控系统,Prometheus于2016年加入CNCF(Cloud Native Computing Foundation,云原生计算基金…...

openGauss学习笔记-130 openGauss 数据库管理-参数设置-重设参数
文章目录 openGauss学习笔记-130 openGauss 数据库管理-参数设置-重设参数130.1 背景信息130.2 GUC参数设置130.3 操作步骤130.4 示例 openGauss学习笔记-130 openGauss 数据库管理-参数设置-重设参数 130.1 背景信息 openGauss提供了多种修改GUC参数的方法,用户可…...
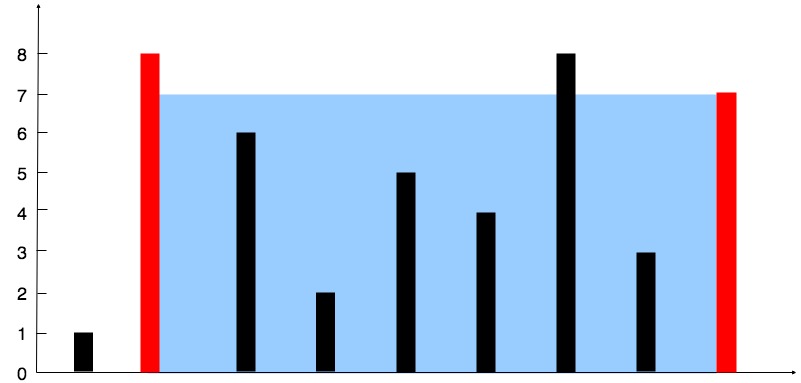
每日OJ题_算法_双指针_力扣11. 盛最多水的容器
力扣11. 盛最多水的容器 11. 盛最多水的容器 - 力扣(LeetCode) 难度 中等 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成…...

数据仓库
一. 各种名词解释 1.1 ODS是什么? ODS层最好理解,基本上就是数据从源表拉过来,进行etl,比如mysql 映射到hive,那么到了hive里面就是ods层。 ODS 全称是 Operational Data Store,操作数据存储.“面向主题的…...
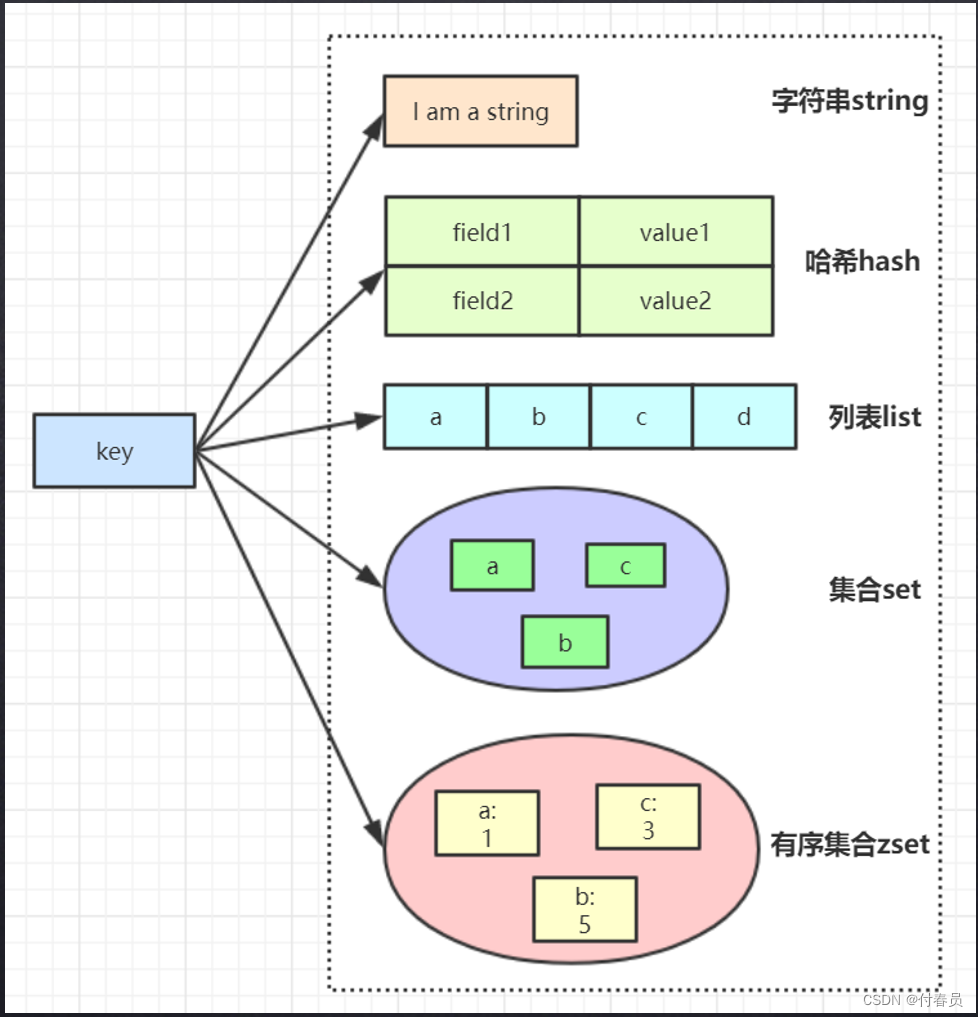
Redis常用操作及应用(一)
一、五种数据结构 二、String结构 1、字符串常用操作 SET key value //存入字符串键值对 MSET key value [key value ...] //批量存储字符串键值对 SETNX key value //存入一个不存在的字符串键值对 GET key //获取一个字符串键值 MGET key [ke…...
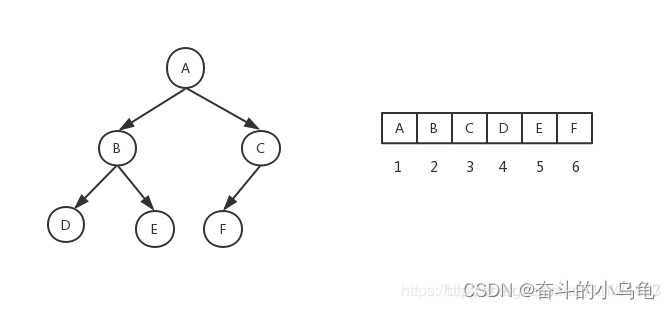
数据结构-树
参考:https://www.hello-algo.com/chapter_tree/binary_tree/#711 1. 介绍 树存储不同于数组和链表的地方在于既可以保证数据检索的速度,又可以保证数据插入删除修改的速度,二者兼顾。 二叉树是一种很重要的数据结构,是非线性的…...
解决ElementUI时间选择器回显出现Wed..2013..中国标准时间.
使用饿了么组件 时间日期选择框回显到页面为啥是这样的? 为什么再时间框中选择日期,回显页面出现了这种英文格式呢???? 其实这个问题直接使用elementui的内置属性就能解决 DateTimePicker 日期时间选择…...

从0到0.01入门 Webpack| 004.精选 Webpack面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
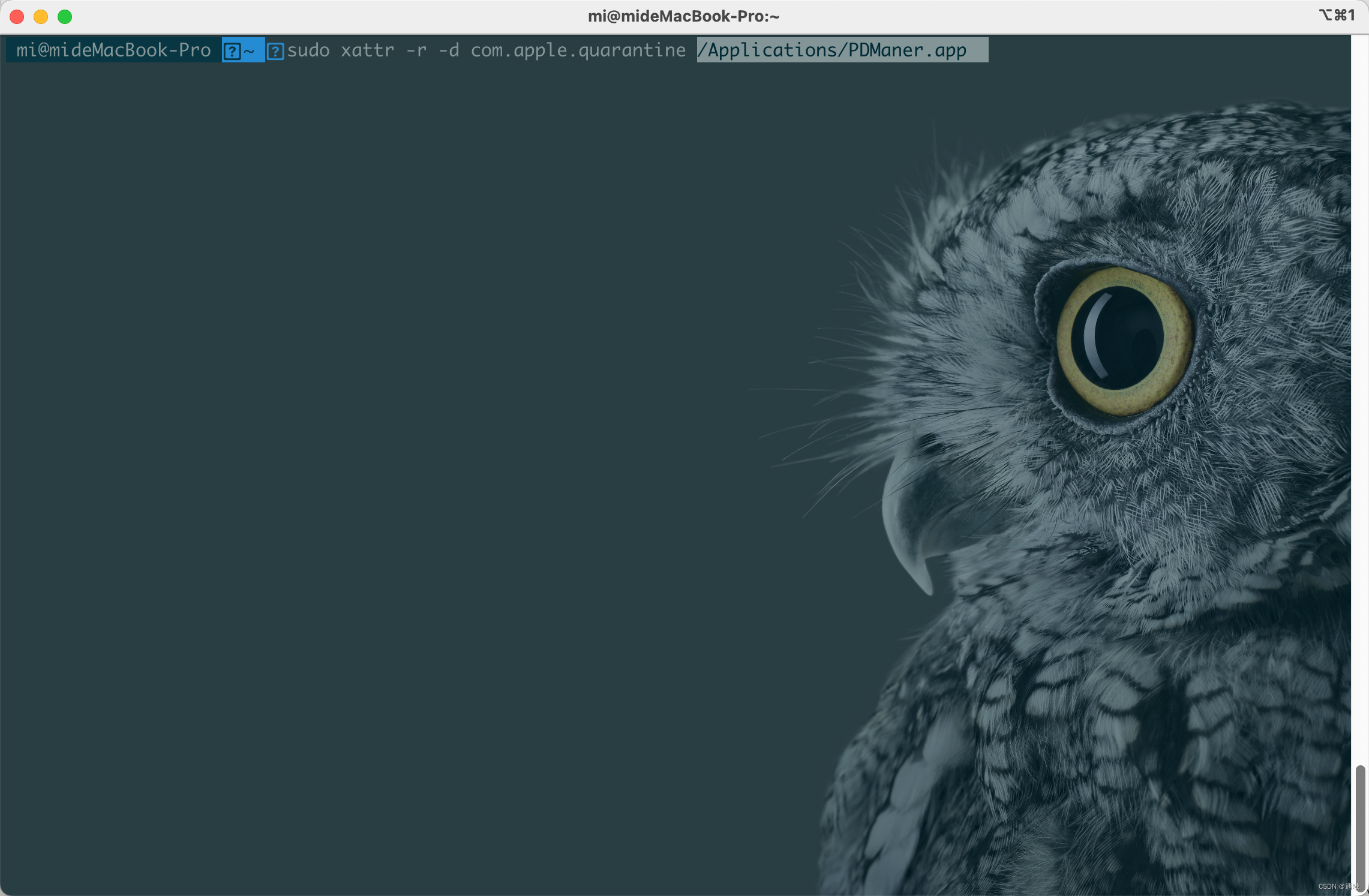
MacOS “xxxxx“,已损坏,无法打开,你应该将它移到废纸篓
在这里插入图片描述 解决方案 应用程序 - 实用工具中打开终端,输入命令, sudo xattr -r -d com.apple.quarantine 然后将程序拖放至命令窗口,如下图:...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...
