数学启发式
学习资料:
优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现
数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍+编程实现+数值实验】学习笔记(Python+Gurobi实现)
大佬到底是大佬!这些资料太适合我这种没基础的人了!
1.什么叫数学启发式,它与启发式的联系与区别
数学启发式(Mathematical Heuristic)是一种基于数学原理、规则或模型的启发式方法。在解决问题时,数学启发式利用数学工具和技术来指导搜索或决策过程,以寻找问题的近似最优解。这种方法通常基于对问题的深刻理解,利用数学建模和分析的手段,设计出一些启发式规则或算法,以提高问题解决的效率和质量。
与一般的启发式相比,数学启发式更强调对问题的数学建模和分析,通过深入理解问题的结构和性质来设计解决方案。数学启发式可以包括对优化、搜索、模拟等数学方法的应用,以便更好地探索解空间并找到良好的解。
联系与区别:
联系: 数学启发式是启发式算法的一种,两者都属于问题解决的方法,都通过某种形式的规则、模型或策略来指导解决方案的生成。数学启发式是在启发式思想的基础上,强调了对问题数学性质的深入理解和利用。
区别: 启发式是一种一般性的问题解决方法,强调通过直觉、经验或规则来指导搜索或决策。数学启发式更加特定,它通过数学建模和分析来指导解决方案,侧重于使用数学工具和技术。在一些问题领域,启发式方法可能更为直观和实用,而在另一些领域,数学启发式可能更为强大,尤其是在需要深刻理解问题结构的情况下。
总体而言,数学启发式是一种借助数学原理来指导问题解决的启发式方法,强调了对问题的深刻数学理解和应用。
User
2. 数学启发式有什么特点,常用的数学启发式有哪些呢?
数学启发式的特点包括对问题进行深入的数学建模和分析,以及利用数学原理指导问题解决的方法。以下是数学启发式的一些特点:
深入数学理解: 数学启发式侧重于对问题进行深入的数学分析和建模。这可能涉及到数学工具、技术、模型等的应用,以更好地理解问题的结构和性质。
问题特定性: 数学启发式通常是问题特定的,它们的设计考虑了问题的具体要求和特点。因此,数学启发式可能需要更多领域专业知识。
精准性和准确性: 数学启发式通常追求更精确和准确的解决方案。通过数学分析,它们旨在提供对问题的深刻理解,并设计出更为有效的算法或规则。
基于理论和模型: 数学启发式往往建立在数学理论或模型的基础上。这可以包括优化理论、概率模型、动态规划等数学工具的运用。
一些常用的数学启发式方法包括:
梯度下降法(Gradient Descent): 用于优化问题的一种方法,通过沿着梯度的反方向来调整参数,以寻找目标函数的最小值。
拉格朗日乘子法(Lagrange Multiplier): 用于求解带约束条件的最优化问题,通过引入拉格朗日乘子将约束条件融入目标函数。
动态规划(Dynamic Programming): 一种通过将问题分解为子问题并保存子问题的解以避免重复计算的优化算法,适用于具有重叠子问题结构的问题。
蒙特卡洛模拟(Monte Carlo Simulation): 利用随机抽样的方法进行数值模拟,用于解决复杂的概率和统计问题。
线性规划(Linear Programming): 用于求解线性约束条件下的最优化问题,通过线性规划模型来描述问题。
这些方法在不同领域和问题类型中得到广泛应用,它们的选择取决于问题的性质和要求。
数学启发式具有一些特点,常见的数学启发式方法包括:
特点:
基于数学原理: 数学启发式是基于数学原理和方法的,强调对问题的数学建模和分析。它通常使用数学工具、技术和结构性的特征来指导问题的解决。
精确性和可解释性: 数学启发式通常以一种更为精确和可解释的方式提供解决方案。通过对问题的深入数学理解,解决方案的生成可以更容易解释和理解。
灵活性: 数学启发式在设计时通常较为灵活,能够适应不同类型的问题。它可以基于问题的特性进行定制,从而在特定问题上表现出色。
优化和搜索: 数学启发式常被用于解决优化问题,其中目标是找到问题的最优解。它们也可以应用于搜索问题,以在大规模解空间中找到合适的解。
理论支持: 数学启发式方法通常具有一定的理论支持,其有效性和性能可能经过分析和证明。
常见数学启发式方法:
凸优化: 利用凸优化理论,将问题转化为凸优化问题,以便更容易找到全局最优解。
数值优化: 使用数值优化方法,例如梯度下降、共轭梯度等,来找到问题的优化解。
动态规划: 通过递推和分阶段求解,将大问题分解为小问题,避免重复计算,提高求解效率。
线性规划: 将问题建模为线性规划问题,利用线性规划算法求解最优解。
离散数学方法: 利用离散数学方法,例如图论、组合优化等,解决离散型问题。
泛函分析: 利用泛函分析方法处理函数空间上的问题,如在优化问题中对函数进行建模和分析。
这些数学启发式方法广泛应用于科学、工程和计算机科学等领域,以解决复杂的实际问题。选择适当的数学启发式方法通常取决于问题的性质和要求。
相关文章:

数学启发式
学习资料: 优化求解器 | Gurobi 数学启发式算法:参数类型与案例实现 数学启发式算法 | 可行性泵 (Feasibility Pump)算法精讲:一份让您满意的【理论介绍编程实现数值实验】学习笔记(PythonGurobi实现) 大佬到底是大佬!这些资料太…...

Win10/Win11 使用Wsl的Ubuntu 子系统搭建CGO环境,相当于Ubuntu下开发。GO环境CGO搭建,支持交叉编译
背景: 之前是使用Mac 开发,最近切换到win11下面。发现使用cgo编译有问题。 下面记载了我的使用方法。 环境: win11(win10理论一样) win11 安装了wsl2的环境,并且安装了ubuntu系统。 在win11 上面安装了g…...

CSS新特性(2-2)
CSS新特性(2-2) 前言box相关box-shadow background背景rgba颜色与透明度transform:rotate(Xdeg) 2D旋转transform:tranlate 平移 前言 本文继续讲解CSS3其他的新特性,想看之前新特性点击这里,那么好本文正式开始。 box相关 box…...
为什么,word文件在只读模式下,仍然能编辑?
Word文档设置了只读模式,是可以编辑的,但是当我们进行保存的时候就会发现,word提示需要重命名并选择新路径才能够保存。 这种操作,即使可以编辑文字,但是原文件是不会受到影响的,编辑之后的word文件会保存到…...

29 - 装饰器模式:如何优化电商系统中复杂的商品价格策略?
开始今天的学习之前,我想先请你思考一个问题。假设现在有这样一个需求,让你设计一个装修功能,用户可以动态选择不同的装修功能来装饰自己的房子。例如,水电装修、天花板以及粉刷墙等属于基本功能,而设计窗帘装饰窗户、…...
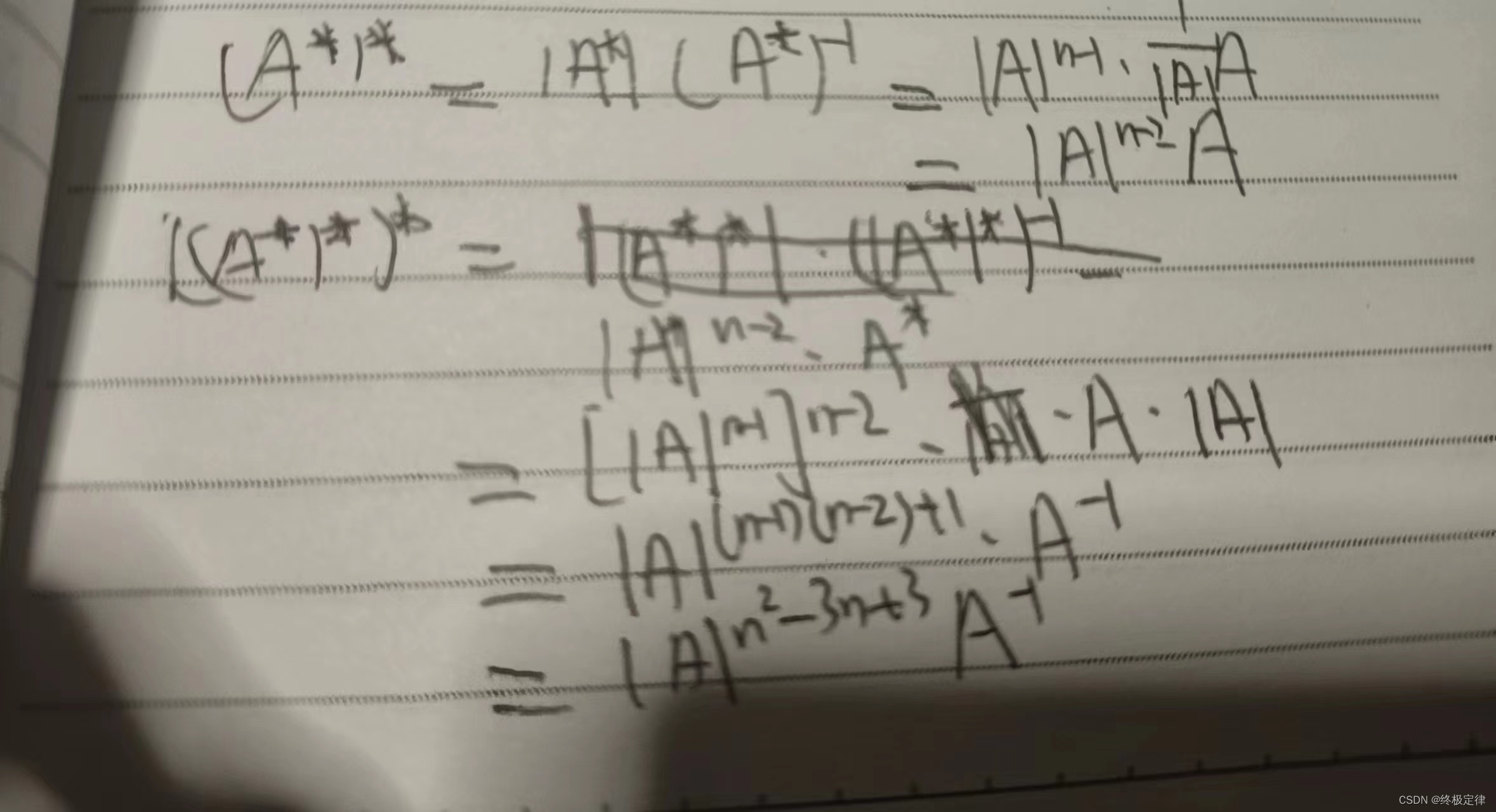
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …...

Ruoyi项目传List到后台并使用Excel模板下载数据的方法以及遇到的各种前后端数据交互问题
import { download } from @/utils/requestconst app = createApp(App)// 全局方法挂载 app.config.globalProperties.download = download 首先因为ruoyi-ui中的main.js有配置如上全局注册: 因此只需要在vue中定义一个方法直接使用this.download调用下载即可: (download的3…...

区块链技术将如何影响未来的数字营销?
你是否听腻了区块链和数字营销等流行语,却不明白它们对未来意味着什么?那么,准备好系好安全带吧,因为区块链技术将彻底改变我们对数字营销的看法。从建立消费者信任到提高透明度和效率,其可能性是无限的。 让我们来探…...

小程序wx:if和hidden的区别?
wx:if:wx:if 是一个完整的条件渲染指令,当它的表达式为真时,才会渲染该指令所在的元素。如果表达式的值为假,则不会渲染该元素。这意味着在表达式为假时,该元素及其子元素都不会被渲染,就像它们从未存在过一…...

分布式幂等
分布式幂等 在分布式系统、网络通信和数据库操作中,幂等性是一个非常重要的概念,特别是在面对可能发生网络故障、消息重复、或者系统崩溃等情况时。 举个简单的例子,考虑一个银行转账的操作。如果转账操作是幂等的,那么无论你执…...

大数据 DataX-Web 详细安装教程
目录 一、DataX-Web 介绍 1.1 DataX-Web 是什么 1.2 DataX-Web 架构 二、DataX-Web 安装部署 2.1 环境要求 2.2 安装 2.3 部署 2.4 数据库初始化 2.5 配置 2.6 启动服务 2.6.1 一键启动所有服务 2.6.2 一键取消所有服务 2.7 查看服务(注意!…...

CSS3媒体查询实现不同宽度的下不同内容的展示
文章目录 前言CSS3 多媒体查询实例520 到 699px 宽度 - 添加邮箱图标700 到 1000px - 添加文本前缀信息大于 1001px 宽度 - 添加邮件地址大于 1151px 宽度 - 添加图标代码后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:CSS ὃ…...

使用 STM32 读取和解析 NTC 热敏电阻的数值
本文介绍了如何利用 STM32 微控制器读取和解析 NTC(Negative Temperature Coefficient)热敏电阻的数值。首先,我们将简要介绍 NTC 热敏电阻的原理和特性。接下来,我们将详细讨论如何设计电路连接和采用合适的 STM32 外设进行数值读…...

C#,数值计算——有理函数插值和外推(Rational_interp)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 有理函数插值和外推 /// Rational Function Interpolation and Extrapolation /// Given a value x, and using pointers to data xx and yy, this routine returns …...

力扣283:移动零(JAVA)
题目描述: 意思是将所有0移到最后的同时其余非0元素位置仍然不变 如 1 2 0 5 2 0 经过移动零后变为 1 2 5 2 0 0 思路:使用双指针的思路来写 fast:从左往右遍历数组 slow:非零元素最后的一个位置 将数组分为3个区间 [0,slow]为处理好的非0数据,slow永远指向最后一个非0数据 [s…...

【statsmodels】快速实现回归预测
python 做线性回归分析有好几种方式,常要的是 scipy 包,statsmodels 包,以及 sklearn包。 但是个人比较喜欢使用statsmodel进行线性回归,一是其可以更好的呈现回归效果,二是其能够自动跳过缺失值。 sklearn则不能方便…...

Kubernetes异常排查方式
集群信息: 1. 显示 Kubernetes 版本:kubectl version 2. 显示集群信息:kubectl cluster-info 3. 列出集群中的所有节点:kubectl get nodes 4. 查看一个具体的节点详情:kubectl describe node <node-name> 5. 列…...

【Linux】:信号的产生
信号 一.前台进程和后台进程1.前台进程2。后台进程3.总结 二.自定义信号动作接口三.信号的产生1.键盘组合键2.kill信号进程pid3.系统调用1.kill函数2.raise函数3.abort函数 四.异常五.软件条件六.通过终端按键产生信号 一.前台进程和后台进程 1.前台进程 一个简单的代码演示 …...

document load 和 document ready 的区别
"document load" 和 "document ready" 都是 JavaScript 中用于处理文档加载事件的术语,但是它们之间有一些重要的区别。 document load 在传统的 JavaScript 中,document.load 事件是当整个 HTML 文档完全加载并出现在浏览器中时触…...

flutter与原生Android通信方式之MethodChannel
闲来无事,flutter好久没看了,上次折腾flutter与Android通信没折腾完,有些事情耽搁了,这次继续 演示效果: flutter与Android原生通信 flutter端 import package:flutter/cupertino.dart; import package:flutter/mater…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
