逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。
1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等)
2.性质二:|ka|=|a|*k的n次方,n为方阵阶数。
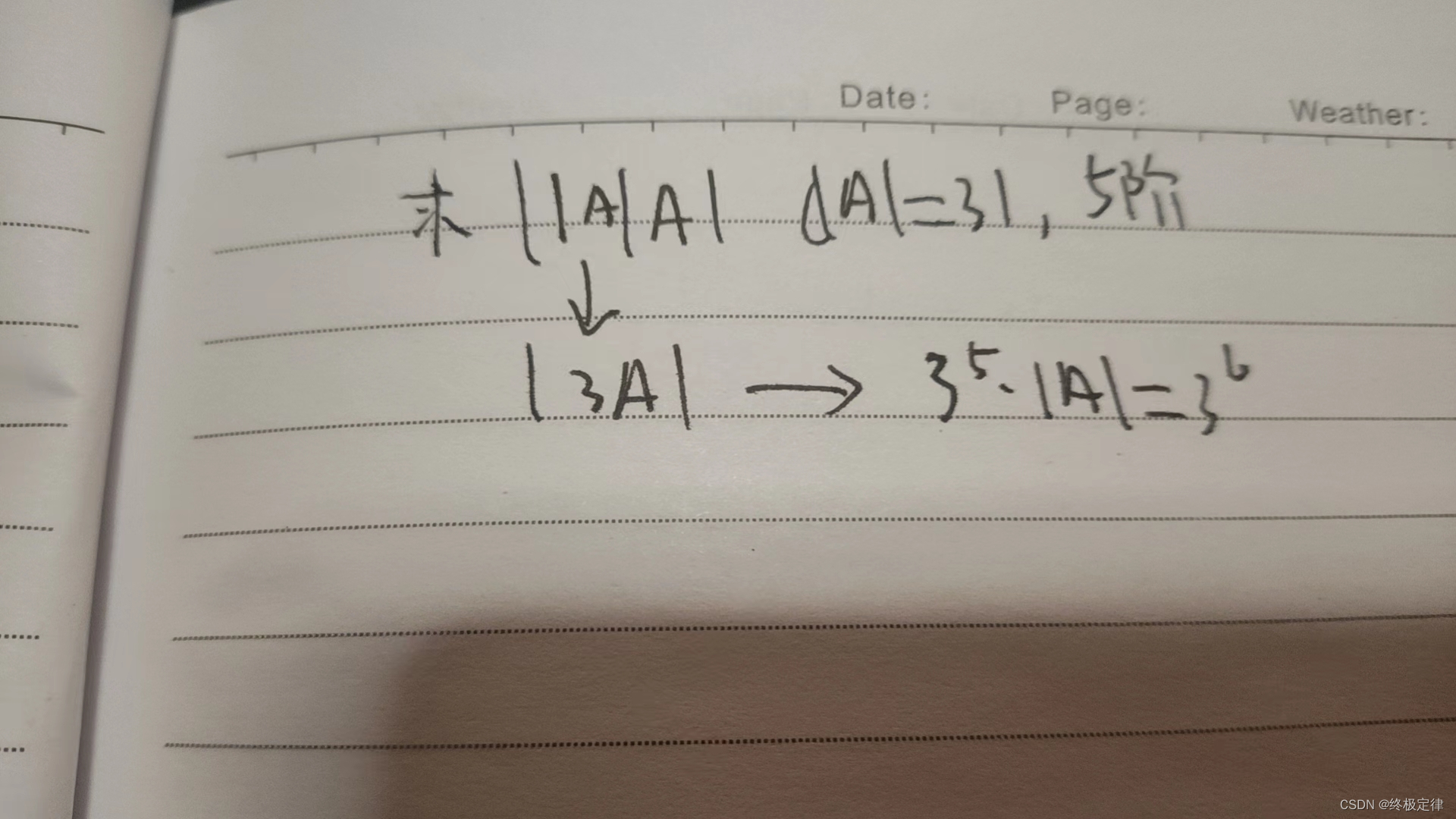
2.伴随矩阵(只有方阵有):计算矩阵的每一个元素的代数余子式,注意-1乘行标加列标,然后每一行的代数余子式按列排放构成矩阵(按行求按列放)(矩阵A的伴随矩阵为A*)
1.AA*=A*A=|A|E(对标性质:某行乘本行代数余子式为行列式的值,乘其他行的等于0)
单位矩阵:主对角线元素都为1其余都为0的方阵
2.任给方阵都有伴随矩阵
3.|A*A|=|A|*|A*|=|A|的n次方(n为阶数),也可写作|A*|=|A|的n-1次方,为左右两边约去A的行列式,一般不能除以行列式,但此处例外
证明过程: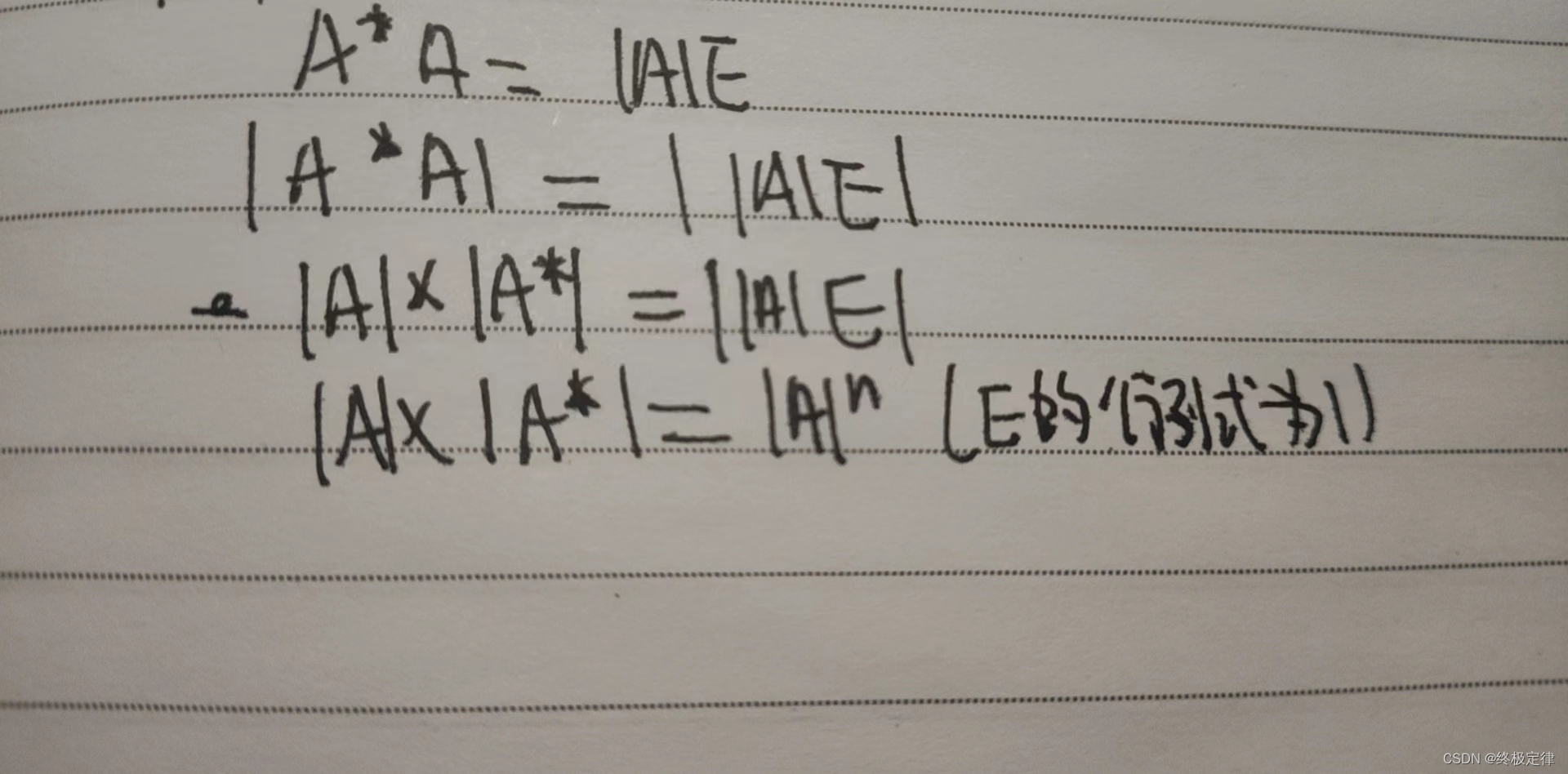
3.逆矩阵:n阶方阵A,存在n阶方阵B使得AB=BA=E,则B为A的逆矩阵,逆矩阵的表示为A的-1次方
1.不是所有的方阵都可逆,比如0矩阵
2.方阵的逆矩阵是为一的,证明过程: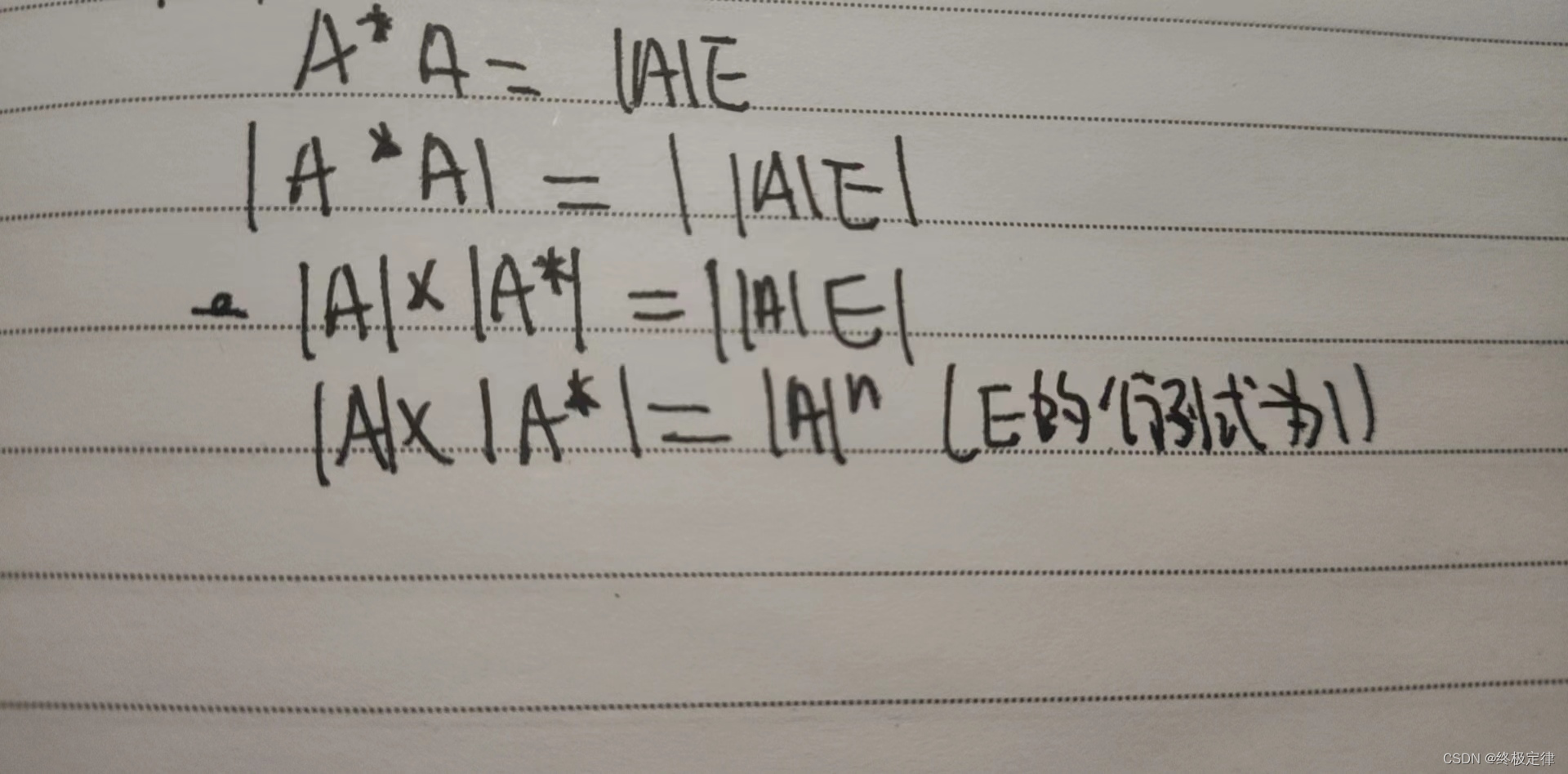
3.A可逆,A的逆矩阵可逆且它的逆矩阵为A(证明用定义然后代换)
4.如果要验证逆矩阵,需要将两个矩阵相乘=E然后配凑
5.A,B都可逆,则AB可逆,且AB的逆矩阵为B的逆矩阵乘A的逆矩阵,注意顺序,证明时写定义式并消去B*B的逆矩阵,当多个矩阵相乘也可以用(类似AB的转置等于B的转置乘A的转置)
6.A可逆其转置也可逆,且A转置的逆等于A逆的转置(转置与逆可以交换顺序)
7.k不等于0,那么kA的逆矩阵等于k分之一乘A的逆矩阵
8,A可逆,A逆的行列式等于A的行列式分之一
9.A可逆,A*可逆,等于A的行列式分之一乘A
4.方阵可逆的条件:行列式不等于0,求法为A的行列式分之一乘A的伴随矩阵,同理A的伴随矩阵等于A的行列式乘A的逆矩阵,运用此求法去代替逆矩阵进行运算时注意A不能为0矩阵
5.做题时只需使用AB=E即可证明A可逆且A的逆矩阵为B
6.在方程中消去一个矩阵可以同时左乘或者右乘它的逆矩阵出现E直接消去
7.求逆矩阵有初等变换法以及伴随矩阵法,首选前者
8.经典例题1
9.经典例题2
例题2总结:
1.提的时候要注意方向
2.矩阵不能同除
3.任何矩阵与数运算都要乘E
4.写任何逆矩阵时都要先证明矩阵可逆
10.经典例题3
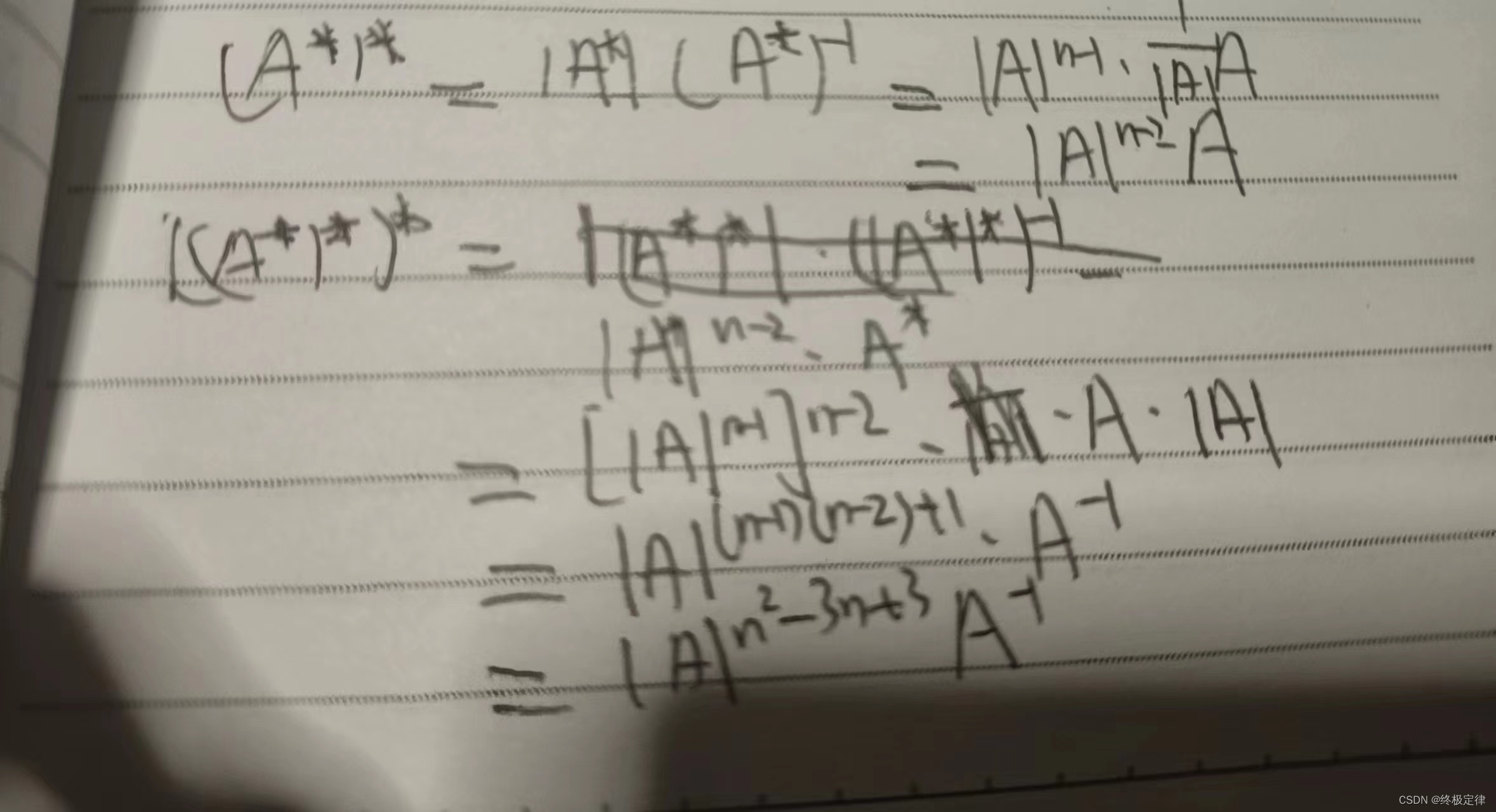
相关文章:
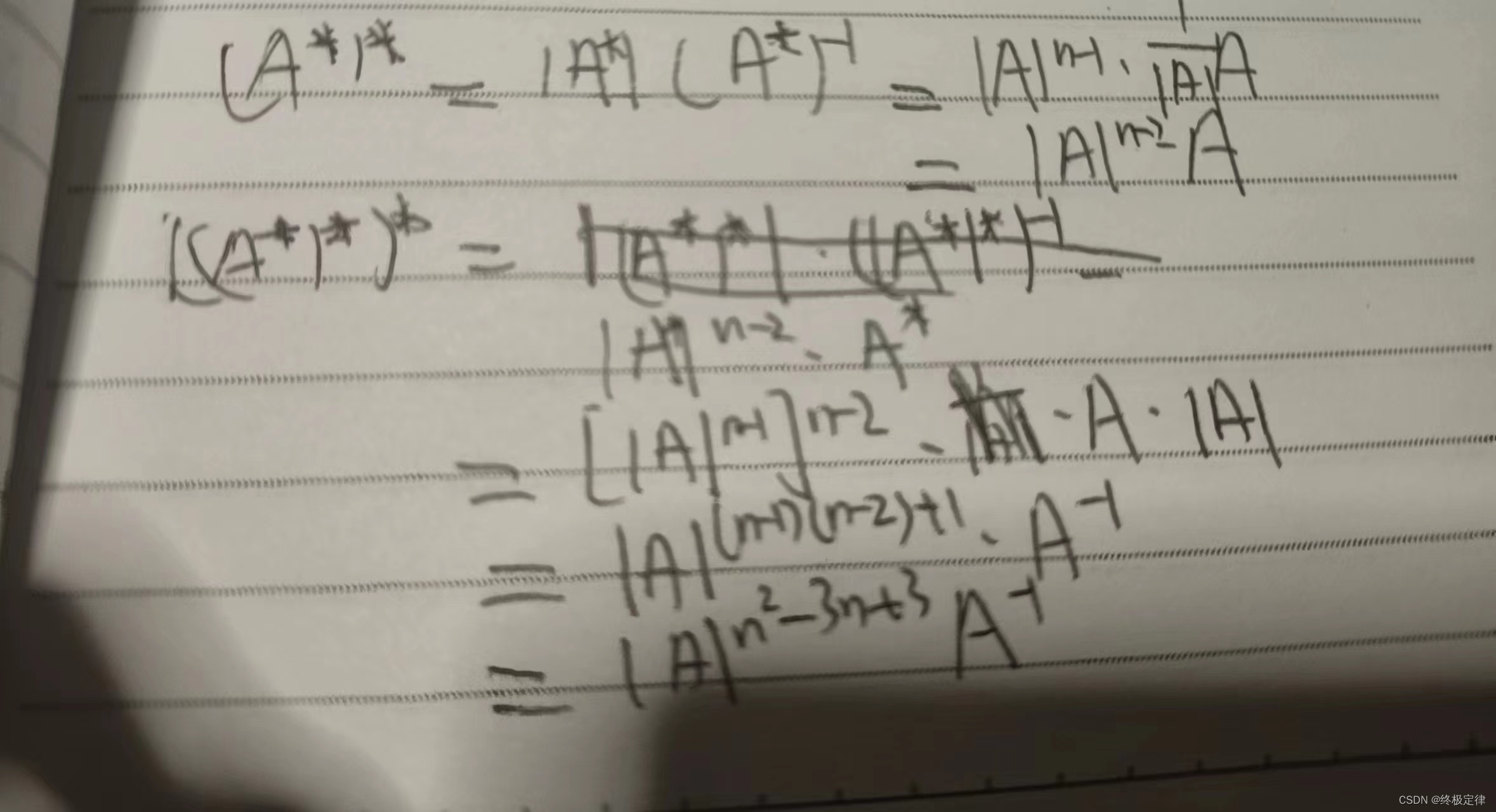
逆矩阵相关性质与例题
1.方阵的行列式:就是将方阵中的每一个元素转换至行列式中。 1.性质一:转置方阵的行列式等于转置前的行列式。(对标性质:行列式与它的转置行列式相等) 2.性质二:|ka||a|*k的n次方,n为方阵阶数。 …...

Ruoyi项目传List到后台并使用Excel模板下载数据的方法以及遇到的各种前后端数据交互问题
import { download } from @/utils/requestconst app = createApp(App)// 全局方法挂载 app.config.globalProperties.download = download 首先因为ruoyi-ui中的main.js有配置如上全局注册: 因此只需要在vue中定义一个方法直接使用this.download调用下载即可: (download的3…...

区块链技术将如何影响未来的数字营销?
你是否听腻了区块链和数字营销等流行语,却不明白它们对未来意味着什么?那么,准备好系好安全带吧,因为区块链技术将彻底改变我们对数字营销的看法。从建立消费者信任到提高透明度和效率,其可能性是无限的。 让我们来探…...

小程序wx:if和hidden的区别?
wx:if:wx:if 是一个完整的条件渲染指令,当它的表达式为真时,才会渲染该指令所在的元素。如果表达式的值为假,则不会渲染该元素。这意味着在表达式为假时,该元素及其子元素都不会被渲染,就像它们从未存在过一…...

分布式幂等
分布式幂等 在分布式系统、网络通信和数据库操作中,幂等性是一个非常重要的概念,特别是在面对可能发生网络故障、消息重复、或者系统崩溃等情况时。 举个简单的例子,考虑一个银行转账的操作。如果转账操作是幂等的,那么无论你执…...

大数据 DataX-Web 详细安装教程
目录 一、DataX-Web 介绍 1.1 DataX-Web 是什么 1.2 DataX-Web 架构 二、DataX-Web 安装部署 2.1 环境要求 2.2 安装 2.3 部署 2.4 数据库初始化 2.5 配置 2.6 启动服务 2.6.1 一键启动所有服务 2.6.2 一键取消所有服务 2.7 查看服务(注意!…...

CSS3媒体查询实现不同宽度的下不同内容的展示
文章目录 前言CSS3 多媒体查询实例520 到 699px 宽度 - 添加邮箱图标700 到 1000px - 添加文本前缀信息大于 1001px 宽度 - 添加邮件地址大于 1151px 宽度 - 添加图标代码后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:CSS ὃ…...

使用 STM32 读取和解析 NTC 热敏电阻的数值
本文介绍了如何利用 STM32 微控制器读取和解析 NTC(Negative Temperature Coefficient)热敏电阻的数值。首先,我们将简要介绍 NTC 热敏电阻的原理和特性。接下来,我们将详细讨论如何设计电路连接和采用合适的 STM32 外设进行数值读…...

C#,数值计算——有理函数插值和外推(Rational_interp)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 有理函数插值和外推 /// Rational Function Interpolation and Extrapolation /// Given a value x, and using pointers to data xx and yy, this routine returns …...

力扣283:移动零(JAVA)
题目描述: 意思是将所有0移到最后的同时其余非0元素位置仍然不变 如 1 2 0 5 2 0 经过移动零后变为 1 2 5 2 0 0 思路:使用双指针的思路来写 fast:从左往右遍历数组 slow:非零元素最后的一个位置 将数组分为3个区间 [0,slow]为处理好的非0数据,slow永远指向最后一个非0数据 [s…...

【statsmodels】快速实现回归预测
python 做线性回归分析有好几种方式,常要的是 scipy 包,statsmodels 包,以及 sklearn包。 但是个人比较喜欢使用statsmodel进行线性回归,一是其可以更好的呈现回归效果,二是其能够自动跳过缺失值。 sklearn则不能方便…...

Kubernetes异常排查方式
集群信息: 1. 显示 Kubernetes 版本:kubectl version 2. 显示集群信息:kubectl cluster-info 3. 列出集群中的所有节点:kubectl get nodes 4. 查看一个具体的节点详情:kubectl describe node <node-name> 5. 列…...

【Linux】:信号的产生
信号 一.前台进程和后台进程1.前台进程2。后台进程3.总结 二.自定义信号动作接口三.信号的产生1.键盘组合键2.kill信号进程pid3.系统调用1.kill函数2.raise函数3.abort函数 四.异常五.软件条件六.通过终端按键产生信号 一.前台进程和后台进程 1.前台进程 一个简单的代码演示 …...

document load 和 document ready 的区别
"document load" 和 "document ready" 都是 JavaScript 中用于处理文档加载事件的术语,但是它们之间有一些重要的区别。 document load 在传统的 JavaScript 中,document.load 事件是当整个 HTML 文档完全加载并出现在浏览器中时触…...

flutter与原生Android通信方式之MethodChannel
闲来无事,flutter好久没看了,上次折腾flutter与Android通信没折腾完,有些事情耽搁了,这次继续 演示效果: flutter与Android原生通信 flutter端 import package:flutter/cupertino.dart; import package:flutter/mater…...

[PyTorch][chapter 66][强化学习-值函数近似]
前言 现实强化学习任务面临的状态空间往往是连续的,无穷多个。 这里主要针对这种连续的状态空间处理。后面DQN 也是这种处理思路。 目录: 1: 原理 2: 梯度更新 3: target 和 预测值 4 流程 一 原理 强化学习最重要的是得到 …...
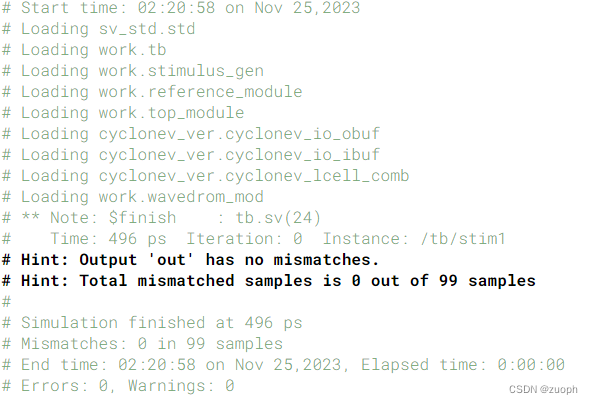
hdlbits系列verilog解答(Exams/m2014 q4e)-46
文章目录 一、问题描述二、verilog源码三、仿真结果 一、问题描述 实现以下电路: 二、verilog源码 module top_module (input in1,input in2,output out);assign out ~(in1 | in2);endmodule三、仿真结果 转载请注明出处!...

小程序如何实现下拉刷新?
一、全局下拉刷新 在app.json的window节点中,将enablePullDownRefresh设置为true; onPullDownRefresh: function () {console.log(下拉刷新);// 在这里编写数据更新的逻辑wx.stopPullDownRefresh(); // 数据更新完成后,调用该方法停止刷新}二…...

二进制数据转换成十六进制表示 binascii.hexlify()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 二进制数据转换成十六进制表示 binascii.hexlify() 选择题 binascii.hexlify()参数的数据类型可以是? import binascii number 11 byte_data number.to_bytes() hex_data bin…...

苍穹外卖--店铺营业状态设置
需求分析和设计 1.1.1 产品原型 进到苍穹外卖后台,显示餐厅的营业状态,营业状态分为营业中和打烊中,若当前餐厅处于营业状态,自动接收任何订单,客户可在小程序进行下单操作;若当前餐厅处于打烊状态&#…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

FTXUI::Dom 模块
DOM 模块定义了分层的 FTXUI::Element 树,可用于构建复杂的终端界面,支持响应终端尺寸变化。 namespace ftxui {...// 定义文档 定义布局盒子 Element document vbox({// 设置文本 设置加粗 设置文本颜色text("The window") | bold | color(…...
