C#,数值计算——有理函数插值和外推(Rational_interp)的计算方法与源程序

1 文本格式
using System;
namespace Legalsoft.Truffer
{
/// <summary>
/// 有理函数插值和外推
/// Rational Function Interpolation and Extrapolation
/// Given a value x, and using pointers to data xx and yy, this routine returns
/// an interpolated value y, and stores an error estimate dy. The returned value
/// is obtained by mm-point polynomial interpolation on the subrange
/// xx[jl..jl + mm - 1].
/// </summary>
public class Rational_interp : Base_interp
{
private double dy { get; set; }
public Rational_interp(double[] xv, double[] yv, int m) : base(xv, yv[0], m)
{
this.dy = 0.0;
}
/// <summary>
/// Given a value x, and using pointers to data xx and yy, this routine returns
/// an interpolated value y, and stores an error estimate dy. The returned
/// value is obtained by mm-point diagonal rational function interpolation on
/// the subrange xx[jl..jl + mm - 1].
/// </summary>
/// <param name="jl"></param>
/// <param name="x"></param>
/// <returns></returns>
/// <exception cref="Exception"></exception>
public override double rawinterp(int jl, double x)
{
const double TINY = 1.0e-99;
int ns = 0;
double[] c = new double[mm];
double[] d = new double[mm];
double hh = Math.Abs(x - xx[jl + 0]);
for (int i = 0; i < mm; i++)
{
double h = Math.Abs(x - xx[jl + i]);
//if (h == 0.0)
if (Math.Abs(h) <= float.Epsilon)
{
dy = 0.0;
return yy[jl + i];
}
else if (h < hh)
{
ns = i;
hh = h;
}
c[i] = yy[jl + i];
d[i] = yy[jl + i] + TINY;
}
double y = yy[jl + ns--];
for (int m = 1; m < mm; m++)
{
for (int i = 0; i < mm - m; i++)
{
double w = c[i + 1] - d[i];
double h = xx[jl + i + m] - x;
double t = (xx[jl + i] - x) * d[i] / h;
double dd = t - c[i + 1];
//if (dd == 0.0)
if (Math.Abs(dd) <= float.Epsilon)
{
throw new Exception("Error in routine ratint");
}
dd = w / dd;
d[i] = c[i + 1] * dd;
c[i] = t * dd;
}
y += (dy = (2 * (ns + 1) < (mm - m) ? c[ns + 1] : d[ns--]));
}
return y;
}
}
}
2 代码格式
using System;namespace Legalsoft.Truffer
{/// <summary>/// 有理函数插值和外推/// Rational Function Interpolation and Extrapolation/// Given a value x, and using pointers to data xx and yy, this routine returns/// an interpolated value y, and stores an error estimate dy. The returned value/// is obtained by mm-point polynomial interpolation on the subrange/// xx[jl..jl + mm - 1]./// </summary>public class Rational_interp : Base_interp{private double dy { get; set; }public Rational_interp(double[] xv, double[] yv, int m) : base(xv, yv[0], m){this.dy = 0.0;}/// <summary>/// Given a value x, and using pointers to data xx and yy, this routine returns/// an interpolated value y, and stores an error estimate dy. The returned/// value is obtained by mm-point diagonal rational function interpolation on/// the subrange xx[jl..jl + mm - 1]./// </summary>/// <param name="jl"></param>/// <param name="x"></param>/// <returns></returns>/// <exception cref="Exception"></exception>public override double rawinterp(int jl, double x){const double TINY = 1.0e-99;int ns = 0;double[] c = new double[mm];double[] d = new double[mm];double hh = Math.Abs(x - xx[jl + 0]);for (int i = 0; i < mm; i++){double h = Math.Abs(x - xx[jl + i]);//if (h == 0.0)if (Math.Abs(h) <= float.Epsilon){dy = 0.0;return yy[jl + i];}else if (h < hh){ns = i;hh = h;}c[i] = yy[jl + i];d[i] = yy[jl + i] + TINY;}double y = yy[jl + ns--];for (int m = 1; m < mm; m++){for (int i = 0; i < mm - m; i++){double w = c[i + 1] - d[i];double h = xx[jl + i + m] - x;double t = (xx[jl + i] - x) * d[i] / h;double dd = t - c[i + 1];//if (dd == 0.0)if (Math.Abs(dd) <= float.Epsilon){throw new Exception("Error in routine ratint");}dd = w / dd;d[i] = c[i + 1] * dd;c[i] = t * dd;}y += (dy = (2 * (ns + 1) < (mm - m) ? c[ns + 1] : d[ns--]));}return y;}}
}
相关文章:

C#,数值计算——有理函数插值和外推(Rational_interp)的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { /// <summary> /// 有理函数插值和外推 /// Rational Function Interpolation and Extrapolation /// Given a value x, and using pointers to data xx and yy, this routine returns …...

力扣283:移动零(JAVA)
题目描述: 意思是将所有0移到最后的同时其余非0元素位置仍然不变 如 1 2 0 5 2 0 经过移动零后变为 1 2 5 2 0 0 思路:使用双指针的思路来写 fast:从左往右遍历数组 slow:非零元素最后的一个位置 将数组分为3个区间 [0,slow]为处理好的非0数据,slow永远指向最后一个非0数据 [s…...

【statsmodels】快速实现回归预测
python 做线性回归分析有好几种方式,常要的是 scipy 包,statsmodels 包,以及 sklearn包。 但是个人比较喜欢使用statsmodel进行线性回归,一是其可以更好的呈现回归效果,二是其能够自动跳过缺失值。 sklearn则不能方便…...

Kubernetes异常排查方式
集群信息: 1. 显示 Kubernetes 版本:kubectl version 2. 显示集群信息:kubectl cluster-info 3. 列出集群中的所有节点:kubectl get nodes 4. 查看一个具体的节点详情:kubectl describe node <node-name> 5. 列…...

【Linux】:信号的产生
信号 一.前台进程和后台进程1.前台进程2。后台进程3.总结 二.自定义信号动作接口三.信号的产生1.键盘组合键2.kill信号进程pid3.系统调用1.kill函数2.raise函数3.abort函数 四.异常五.软件条件六.通过终端按键产生信号 一.前台进程和后台进程 1.前台进程 一个简单的代码演示 …...

document load 和 document ready 的区别
"document load" 和 "document ready" 都是 JavaScript 中用于处理文档加载事件的术语,但是它们之间有一些重要的区别。 document load 在传统的 JavaScript 中,document.load 事件是当整个 HTML 文档完全加载并出现在浏览器中时触…...

flutter与原生Android通信方式之MethodChannel
闲来无事,flutter好久没看了,上次折腾flutter与Android通信没折腾完,有些事情耽搁了,这次继续 演示效果: flutter与Android原生通信 flutter端 import package:flutter/cupertino.dart; import package:flutter/mater…...

[PyTorch][chapter 66][强化学习-值函数近似]
前言 现实强化学习任务面临的状态空间往往是连续的,无穷多个。 这里主要针对这种连续的状态空间处理。后面DQN 也是这种处理思路。 目录: 1: 原理 2: 梯度更新 3: target 和 预测值 4 流程 一 原理 强化学习最重要的是得到 …...
hdlbits系列verilog解答(Exams/m2014 q4e)-46
文章目录 一、问题描述二、verilog源码三、仿真结果 一、问题描述 实现以下电路: 二、verilog源码 module top_module (input in1,input in2,output out);assign out ~(in1 | in2);endmodule三、仿真结果 转载请注明出处!...

小程序如何实现下拉刷新?
一、全局下拉刷新 在app.json的window节点中,将enablePullDownRefresh设置为true; onPullDownRefresh: function () {console.log(下拉刷新);// 在这里编写数据更新的逻辑wx.stopPullDownRefresh(); // 数据更新完成后,调用该方法停止刷新}二…...

二进制数据转换成十六进制表示 binascii.hexlify()
【小白从小学Python、C、Java】 【计算机等考500强证书考研】 【Python-数据分析】 二进制数据转换成十六进制表示 binascii.hexlify() 选择题 binascii.hexlify()参数的数据类型可以是? import binascii number 11 byte_data number.to_bytes() hex_data bin…...

苍穹外卖--店铺营业状态设置
需求分析和设计 1.1.1 产品原型 进到苍穹外卖后台,显示餐厅的营业状态,营业状态分为营业中和打烊中,若当前餐厅处于营业状态,自动接收任何订单,客户可在小程序进行下单操作;若当前餐厅处于打烊状态&#…...

2023金盾杯线上赛-AGRT战队-WP
目录 WEB ApeCoin get_source ezupload easyphp MISC 来都来了 芙宁娜 Honor Crypto 我看看谁还不会RSA hakiehs babyrsa PWN sign-format RE Re1 WEB ApeCoin 扫描发现有源码泄露,访问www.tar.gz得到源码。 在源码中发现了冰蝎马。 Md5解码&am…...

Python面向对象编程——类方法、实例方法和静态方法总结
在Python面向对象编程中,类方法(class methods)、实例方法(instance methods)和静态方法(static methods)是不同类型的方法,它们有一些联系,但也存在一些明显的区别。 类…...
:常用基础组件)
HarmonyOS开发(五):常用基础组件
1、组件介绍 组件(Component),是界面搭建及显示的最小单元。 组件根据功能可以分为五大类:基础组件、容器组件、媒体组件、绘制组件、画布组件 2、基础组件 基础组件是视图层的基本组成单元,它包含:Text、Image、T…...
)
Hive中常出现的错误(不定时更新)
1.加载数据失败 hive> load data local inpath /home/user/hive.txt into table studentl> ; FAILED: SemanticException [Error 10001]: Line 1:56 Table not found studentl hive> load data local inpath /home/user/hive.txt into table student; Loading data to…...

c++ 重写 多态
1 重写(继承后(拼接基类后)) 1.1 非虚函数 同名成员函数 (各自有一个xFunction() 内存 ) #include <iostream> #include <String> class BaseClass { public:void xFunction() {std::cout << "BaseClass::xFunction()\n"; } };class Subclass1 …...
用户名称(user.name)和邮箱(user.email))
Git如何修改提交(commit)用户名称(user.name)和邮箱(user.email)
Git用户名 Git查看用户名 git config user.name修改Git提交用户名 修改全局Git用户名 git config --global user.name "xx" 修改当前服务/项目Git用户名 git config user.name "xx"如果出现以下错误,解决方案如下: 错误案例&am…...
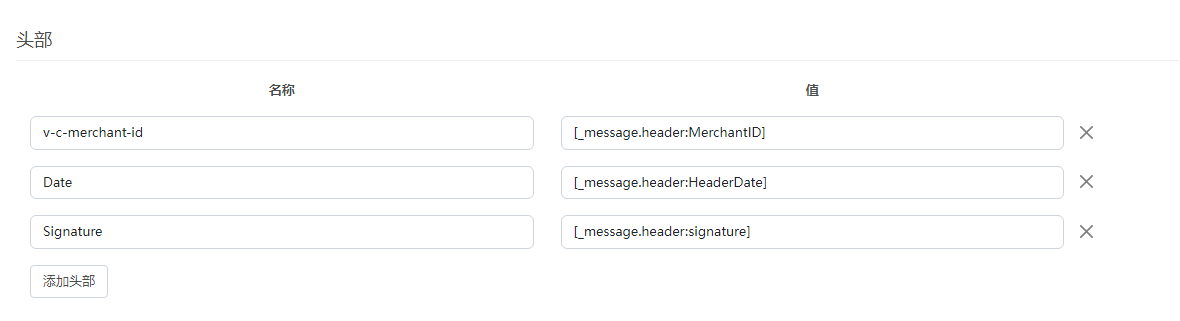
知行之桥EDI系统HTTP签名验证
本文简要概述如何在知行之桥EDI系统中使用 HTTP 签名身份验证,并将使用 CyberSource 作为该集成的示例。 API 概述 首字母缩略词 API 代表“应用程序编程接口”。这听起来可能很复杂,但真正归结为 API 是一种允许两个不同实体相互通信的软件。自开发以…...
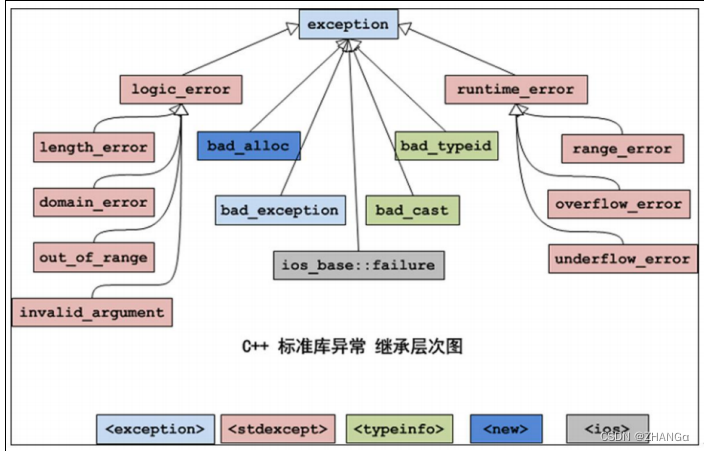
C++ DAY08 异常
概念 异常事件(如:除 0 溢出,数组下标越界,所要读取的文件不存在 , 空指针,内存不足 等等) 在 C 语言对错误的处理是两种方法: 一是使用整型的返回值标识错误; 二是使用 errn…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
