C#,《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码

1 文本格式
/// <summary>
/// 《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码
/// 方差 = SUM((Xi - X)^2 ) / n i=0...n-1 X = Average of X[i]
/// 方差是 (各数值减去平均值)的平方 之和,再除以个数。
/// 方差的平方 = 标准差,反之,开平方即可。
/// 本课是为了验证前面的正态分布函数。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button18_Click(object sender, EventArgs e)
{
// 随机数个数
int m = 50000;
// 随机数的范围(0---1023)
int n = 1024;
int[] num = new int[m];
int i = 0;
while (i < m)
{
// 按正太分布生成随机数
// 平均值 = 0.5 * n
// 标准差 = 0.1 * n
int a = (int)(Rand(0.5, 0.1) * n);
if (a < 0) continue;
if (a >= n) continue;
num[i++] = a;
}
// 计算平均值
double sum = 0.0;
for (int j = 0; j < m; j++)
{
sum += num[j];
}
double avg = sum / (double)m;
// 计算方差
double delta = 0.0;
for (int j = 0; j < m; j++)
{
// 原始写法
//delta = delta + (num[j] - avg) * (num[j] - avg);
// 另一种写法
delta += Math.Pow((num[j] - avg), 2);
}
// 方差
double variance_1 = delta / (double)m;
// 标准差
double standard_variance_1 = Math.Sqrt(delta / (double)(m)) / (double)n;
#region 更严肃的算法,应该先进行数据规范化,
// 将数据规整到(0 --- 1.0)再计算方差等等。
double[] xnum = new double[m];
for (int j = 0; j < m; j++)
{
xnum[j] = num[j] / (double)n;
}
// 均值也需要规范化
avg /= n;
// 计算方差
delta = 0.0;
for (int j = 0; j < m; j++)
{
delta += Math.Pow((xnum[j] - avg), 2.0);
}
double standard_variance_2 = Math.Sqrt(delta / (double)(m));
#endregion
StringBuilder sb = new StringBuilder();
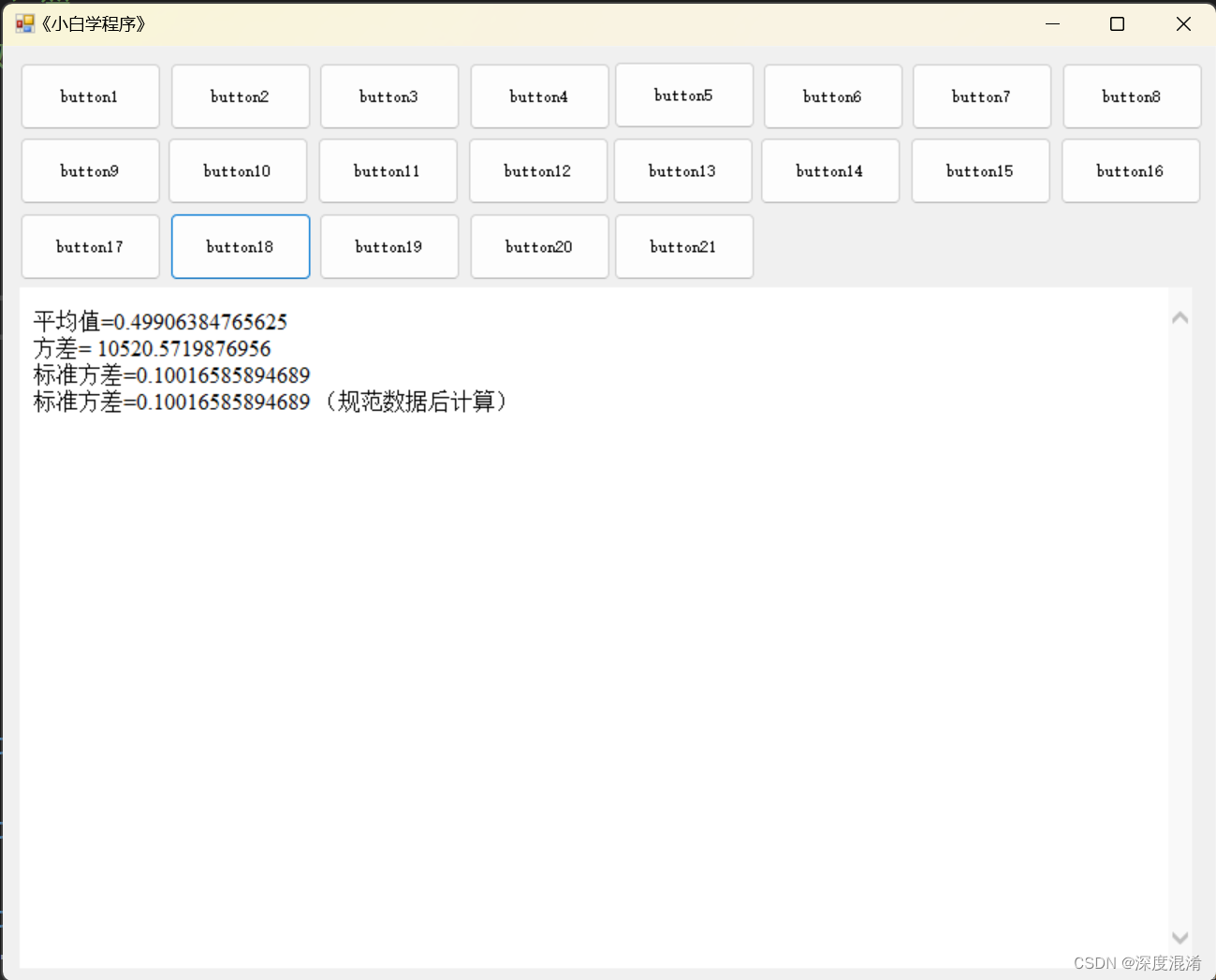
sb.AppendLine("平均值=" + avg + "<br>");
sb.AppendLine("方差= " + variance_1 + "<br>");
sb.AppendLine("标准方差=" + standard_variance_1 + "<br>");
sb.AppendLine("标准方差=" + standard_variance_2 + " (规范数据后计算)<br>");
webBrowser1.DocumentText = sb.ToString();
}
2 代码格式
/// <summary>
/// 《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码
/// 方差 = SUM((Xi - X)^2 ) / n i=0...n-1 X = Average of X[i]
/// 方差是 (各数值减去平均值)的平方 之和,再除以个数。
/// 方差的平方 = 标准差,反之,开平方即可。
/// 本课是为了验证前面的正态分布函数。
/// </summary>
/// <param name="sender"></param>
/// <param name="e"></param>
private void button18_Click(object sender, EventArgs e)
{// 随机数个数int m = 50000;// 随机数的范围(0---1023)int n = 1024;int[] num = new int[m];int i = 0;while (i < m){// 按正太分布生成随机数// 平均值 = 0.5 * n// 标准差 = 0.1 * nint a = (int)(Rand(0.5, 0.1) * n);if (a < 0) continue;if (a >= n) continue;num[i++] = a;}// 计算平均值double sum = 0.0;for (int j = 0; j < m; j++){sum += num[j];}double avg = sum / (double)m;// 计算方差double delta = 0.0;for (int j = 0; j < m; j++){// 原始写法//delta = delta + (num[j] - avg) * (num[j] - avg);// 另一种写法delta += Math.Pow((num[j] - avg), 2);}// 方差double variance_1 = delta / (double)m;// 标准差double standard_variance_1 = Math.Sqrt(delta / (double)(m)) / (double)n;#region 更严肃的算法,应该先进行数据规范化,// 将数据规整到(0 --- 1.0)再计算方差等等。double[] xnum = new double[m];for (int j = 0; j < m; j++){xnum[j] = num[j] / (double)n;}// 均值也需要规范化avg /= n;// 计算方差delta = 0.0;for (int j = 0; j < m; j++){delta += Math.Pow((xnum[j] - avg), 2.0);}double standard_variance_2 = Math.Sqrt(delta / (double)(m));#endregionStringBuilder sb = new StringBuilder();sb.AppendLine("平均值=" + avg + "<br>");sb.AppendLine("方差= " + variance_1 + "<br>");sb.AppendLine("标准方差=" + standard_variance_1 + "<br>");sb.AppendLine("标准方差=" + standard_variance_2 + " (规范数据后计算)<br>");webBrowser1.DocumentText = sb.ToString();
}
3 计算结果
相关文章:

C#,《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码
1 文本格式 /// <summary> /// 《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码 /// 方差 SUM((Xi - X)^2 ) / n i0...n-1 X Average of X[i] ///…...

【版本管理 | Git 】Git最佳实践系列(一) —— LFS .gitignore 最佳实践,确定不来看看?
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

【Linux】驱动程序同步和异步通知方式
一、应用程序APP,访问驱动程序/dev/input/enent1流程: 假设用户程序直接访问 /dev/input/event0 设备节点,或者使用 tslib 访问设备节点,数据的流程如下: APP 发起读操作,若无数据则休眠;用户操…...

移动机器人路径规划(七)--- 基于MDP的路径规划MDP-Based Planning
目录 1 什么是MDP-Based Planning 2 worst-case analysis for nondeterministic model 3 Expected Cost Planning 4 Real Time Dynamic Programming(RTDP) 1 什么是MDP-Based Planning 之前我们从起点到终点存在很多可执行路径,我们可以…...

vue--The template root requires exactly one element.的解决办法
[vue/no-multiple-template-root] The template root requires exactly one element.eslint-plugin-vue 在vue中会出现以上问题 这是因为vue的模版中只有能一个根节点,所以在<template>中插入第二个元素就会报错 解决方案: 将<template>…...

嵌入式软件开发学习途径推荐
1、概述 嵌入式系统是当今智能化的重要组成部分,广泛应用于各行业和领域。学习内容多而杂,不同行业学习的内容也有一定差异。学习完一些基础课程后,工作中便是用到或根据就业方向去拓展自己的知识。这里推荐如下途径(后续可能会补充)…...
图书管理系统源码,图书管理系统开发,图书借阅系统源码三框架设计原理和说明
TuShuManger项目简介和创建 这里一共设计了6个项目,主要是借助三层架构思想分别设计了主要的三层,包括model实体层,Dal数据库操作层,Bll业务调用层,其他有公共使用项目common层,DButitly提取出来的数据库访问层,下面我们分别创建每个项目和开始搭建整个过程 TuShuManger…...

服务器被入侵了怎么去排查
在当今数字化时代,网络安全问题变得越来越重要。其中,服务器被入侵是一种常见的安全威胁。当服务器被入侵时,我们需要采取一系列措施来排查和解决问题。本文将为您提供服务器被入侵后的排查步骤。 第一步:确认服务器被入侵 当发现…...
、instanceOf和Array.isArray()的区别)
JavaScript中Object.prototype.toString.call()、instanceOf和Array.isArray()的区别
JavaScript是一种非常流行的编程语言,它具有许多强大的功能和特性。在JavaScript中,有一些方法和操作符可以帮助我们更好地处理数据类型和对象。本文将重点讨论Object.prototype.toString.call()、instanceOf和Array.isArray()这三个在JavaScript中常用的…...

Java串口通信入门教程
简介 串口通信是一种用于在计算机和外部设备之间进行数据交换的通信方式。在许多应用场景中,如物联网、自动化控制等领域,串口通信被广泛应用。本教程将带领您入门Java串口通信,介绍串口通信的基本原理和Java中的串口通信库,并提…...
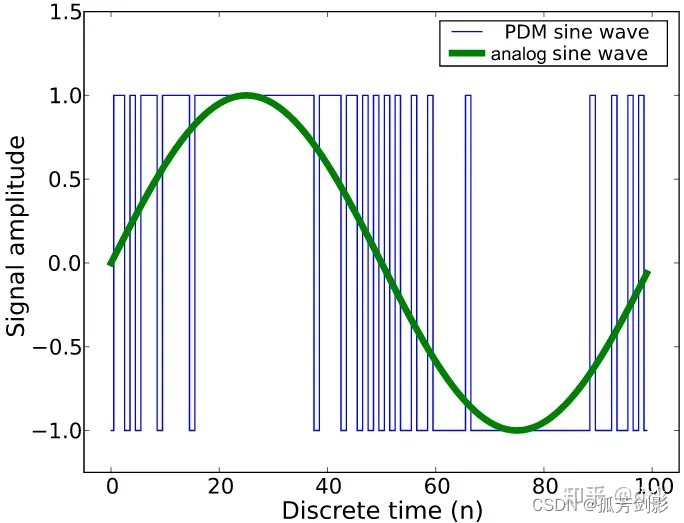
音频采集的相关基础知识
本文引注: https://zhuanlan.zhihu.com/p/652629744 1.麦克风的种类 (1)模拟麦克风 ECM麦克风:驻极体电容麦克风(ECM),典型的汽车ECM麦克风是一种将ECM单元与小型放大器电路整合在单个外壳中的装置。放大器提供一个模拟信号,其电压电平允许…...

vue中 多个请求,如果一个请出错,页面继续执行
vue中 多个请求,如果一个请出错,页面继续执行 在Vue中,可以通过Promise.all()方法来处理多个请求,即使其中一个请求出错,页面也可以继续执行其他的逻辑。 下面是一个示例代码,演示了如何在Vue中处理多个请…...
飞翔的小鸟小游戏
主类 package APP;import 框架.GameFrame;public class GameApp {public static void main(String[] args) {//游戏的入口new GameFrame();} }场景实物 package 框架;import 图导.Constant; import 图导.GameUtil;import java.awt.*; import java.awt.image.BufferedImage; …...

Visual Studio(VS) C++程序LNK2005错误,提示“error LNK2005: _XXX已经在xxx.obj中定义”解决方案
1.问题如图 2.出现原因 项目中有多个源文件或头文件,include后导致有些变量重复定义,加上Visual Studio新版版要求更严格 3.解决办法 查询到的解决办法很多不好用,此处记录解决自己问题的一个办法:直接让编译器忽略第二次定义的…...
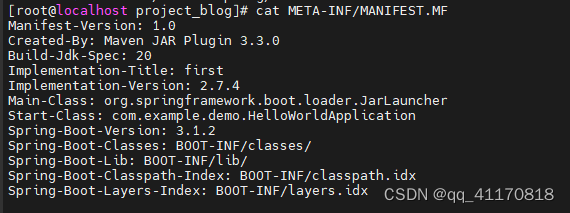
linux部署jar 常见问题
1.java -jar xxx.jar no main manifest attribute, in xxx.jar 一.no main manifest attribute, in xxx.jar 在pom.xml文件中加入: <plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifac…...

Arrays.asList() 与 Collections.singletonList()的恩怨情仇
1. 概述 列表是我们使用 Java 时常用的集合类型。 众所周知,我们可以轻松地用一行初始化一个List。例如,当我们想要初始化一个只有一个元素的List时,我们可以使用Arrays.asList()方法或Collections.singletonList()方法。 在本文中&#x…...
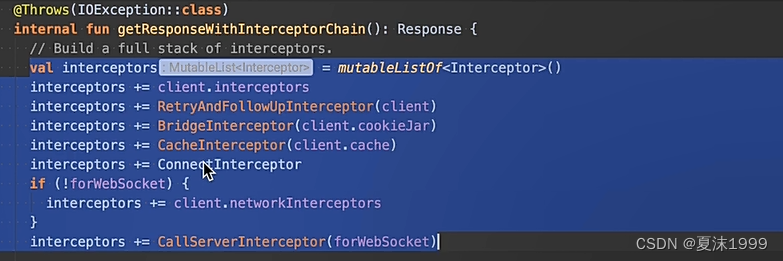
Okhttp 浅析
安全的连接 OkHttpClient: OkHttpClient: 1.线程调度 2.连接池,有则复用,没有就创建 3.interceptor 4.interceptor 5.监听工厂 6.是否失败重试 7.自动修正访问,如果没有权限或认证 8是否重定向 followRedirects 9.协议切换时候是否继续重定向 10.Cookie jar 容器 默认…...
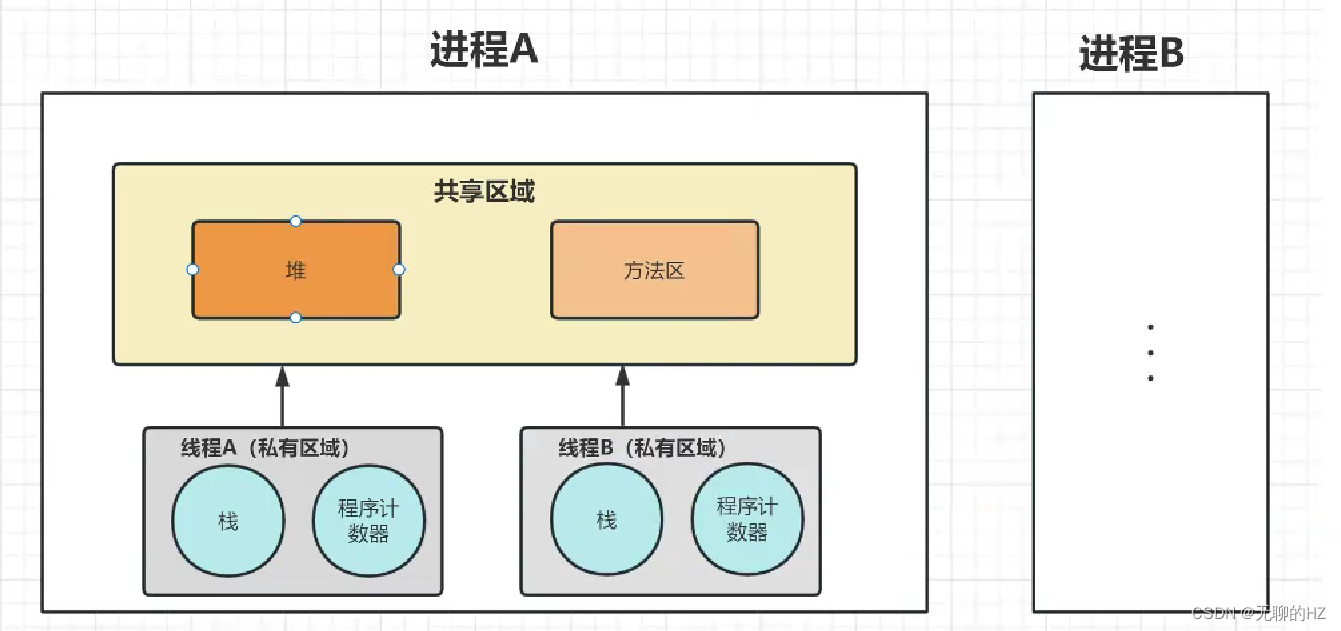
面试常见问题:什么是进程? 什么是线程?进程和线程有什么区别?
1.什么是进程? 进程是操作系统中一个程序在执行过程中的一个实例,每个进程都有自己独立的地址空间,进程间不共享内存。它是程序运行的最小内存单元; 进程特点: 1> 需要占用独立的内存空间; 2>可以并…...

什么是SQL?
SQL和MySQL是当今计算机领域中非常重要的两个概念。SQL是关系型数据库的查询语言,而MySQL是一种关系型数据库管理系统。它们在数据存储、管理和查询方面发挥着巨大的作用。在本文中,我们将深入探讨SQL和MySQL的定义、功能、应用以及它们之间的联系。 一…...
人力资源管理后台 === 基础环境+登陆
目录 1.人力资源项目介绍 1.1 项目架构和解决方案 1.2 课程安排 1.3 课程具备能力 1.4 课程地址 2. 拉取项目基础代码 3.项目目录和入口文件介绍 4.App.vue根组件解析 5.基础设置settings.js和导航守卫permission.js 6.Vuex的结构 7.使用模板中的Icon图标 8.扩展…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...

中国政务数据安全建设细化及市场需求分析
(基于新《政务数据共享条例》及相关法规) 一、引言 近年来,中国政府高度重视数字政府建设和数据要素市场化配置改革。《政务数据共享条例》(以下简称“《共享条例》”)的发布,与《中华人民共和国数据安全法》(以下简称“《数据安全法》”)、《中华人民共和国个人信息…...
