NVMe-oF E-JBOF设计解析:WD RapidFlex网卡、OpenFlex Data24

OpenFlex Data24 NVMe-oF Storage Platform
WD的SN840 NVMeSSD新品并没有太吸引我注意,因为它还是PCIe 3.0接口的,要知道Intel的PCIe 4.0 SSD都已经推出了。
但上面这个NVMe-oF(NVMe over Fabric)EBOF(区别于普通JBOF的第一个字母表示Ethernet)我就有点兴趣了。前一段看到刘爱贵博士的公司——大道云行宣布的分布式软件定义存储新品,使用了一家国内的E-JBOF,想从官网找公开资料学习下都不太多。在这点上国际品牌往往要做得完善一些,否则我也写不出本文的分享。
从SAS JBOD到NVMe JBOF和EBOF
谈到NVMe JBOF的前身,SAS JBOD磁盘(HDD/SSD)扩展柜不得不提,下面只用一张图简单交代下JBOD里的SAS Expander控制模块。

上图从10年前的一段视频里截出,可以说是LSI在6Gb/s SAS时代的经典之一(Dell PowerVault MD1200/1220 JBOD基本相同),也勾起了我一段曾经美好的回忆。2U驱动器机箱里有2个HA路径的SAS Expander——只用LSI SAS2X36芯片作为核心即可。
相比之下,NVMe-oFJBOF/EBOF至少要在物理上把PCIe转换为以太网,所以结构不可能如此简单。我们先来看看下面这块“网卡”。

这颗芯片的型号是WDRapidFlex A1000 NVMe-oF ASIC,对应的板卡为RapidFlex C1000 NVMe-oF Adapter,不难看出是用来干啥的。规格如下:

其网口部分提供1个100GbE或者2个50/25GbE以太网,协议支持RoCE、iWARP/TCP,看产品名称自然也支持NVMe。PCIe接口支持Root Complex,看来是用于连接NVMe SSD的;PCIe Gen3 x16还能拆分成2个x8来使用(连接多个PCIeSwitch)。

上图是基于RapidFlex A1000的EBOF参考架构。位于机箱前部的NVMe SSD通过热插拔背板连接到2块控制电路板——应该支持双端口SSD的2个PCIe 3.0 x2多路径访问,然后经过PCIe Switch之后,就连接到几个RapidFlex A1000 ASIC对前端服务器提供NVMe-oF访问。同时有BMC / 机箱服务模块用于带外管理。

看这个WD单芯片解决方案就更清楚了。所谓“6-way无阻塞内存子系统”,其实RapidFlex A1000 ASIC是无需DRAM内存工作的,它的工作其实很单一——就是那个“MPU”实现NVMe(连接SSD)到NVMe-oF(over RDMA)之间的转换。

再来看看WD OpenFlex Data24 NVMe JBOF(EBOF)的后视图。左右2个IOM模块上各自可以插3块网卡,应该就是前面提到的RapidFlex C1000 NVMe-oF Adapter。

这里重点看一下OpenFlex Data24的高可用和性能设计。在2个IOM模块中,每个上面应该是用了不低于96 lane PCIe 3.0 Switch芯片——下行48 lane连接NVMe SSD,然后3个x16连接RapidFlex网卡。除了到以太网那里带宽打一点折扣之外,PCIe链路的“收敛比”是1:1性能无损的。

OpenFlex Data24给出的性能指标是13.2M IOPS和70.7GB/s,平均每块SSD接近55万IOPS和3GB/s带宽,这个几乎把6个100GbE网口跑满了,每块网卡平均220万IOPS。
这里友情插一个小小的广告,有想咨询西数企业存储产品商务方面的朋友,可以联系圈内名人刘委员(平台小秘书),靠谱的哥们儿,他的微信号wood6988。
NVMe-oF EBOF高级实现方式、闪存阵列的区别
前面讨论的WD产品只是最基本的以太网JBOF,可以说与SAS JBOD和PCIeNVMe JBOF的地位没有本质区别——支持用来连接盘,而并没有更多高级管理功能。再往上一点的方案是什么呢?下面我拿Mellanox和Broadcom的产品来简单举个例。
关于MellanoxBlueField我有2篇写的比较早,收录在《存储网络交换、NVMe oF》专辑中,大家也可以找最新的资料看看。

上图这款卡,在WinnieShao博士的大作《智能网卡SmartNIC:“大”x86 Server中的“小”armServer》中也被提到过。BroadcomStingray板卡的主控芯片BCM58800也是一颗ARM SoC,它在拓扑图中的位置有点类似于前面的WD RapidFlex,但既然敢称为闪存阵列(Flash Array)而不只是E-JBOF自然有所不同。

上图这份资料有点老。ARM和网卡部分我就不多谈了,Broadcom本身就是做网络出身的。SoC同时包含双通道DDR4内存控制器,具备接近100Gb/s Hash和加密引擎(也能用于重删)、RAID 5 XOR和RAID 6 P+Q Galois/Erasure纠删码支持。
除了基于RDMA的NVMe-oF之外,StingraySmartNIC的应用方案还包括NVMe-TCP(扩展阅读:《NVMe over TCP:iSCSI的接班人?》),这一点我理解WD RapidFlex网卡就做不到了。类似的还有对象存储,已经超出了JBOF/EBOF的基本功能范畴。
关于存储服务offload卸载这一块,如果是传统企业存储市场中功能强大的闪存阵列,只靠SmartNIC显然又不够了。下图引用自《DellEMC PowerStore详解:NVMe+SAS全闪存阵列,还是一体机?》,只是举个例。

关于写缓存镜像,以及数据缩减(压缩/重删)处理,只是PowerStore存储系统数据路径中的一部分流程而已。其实我理解NVRAM盘只是为了保障数据的持久化(估计是一个副本),真正的处理还是要放在DRAM主内存中才能高效。至于更多的高级存储服务,就需要用到控制器中强大的服务器级别CPU了(具体到PowerStore使用的是XeonScalable)。
相关文章:

NVMe-oF E-JBOF设计解析:WD RapidFlex网卡、OpenFlex Data24
OpenFlex Data24 NVMe-oF Storage Platform WD的SN840 NVMeSSD新品并没有太吸引我注意,因为它还是PCIe 3.0接口的,要知道Intel的PCIe 4.0 SSD都已经推出了。 但上面这个NVMe-oF(NVMe over Fabric)EBOF(区别于普通JBO…...
visual studio 下的git
我这个是看视频笔记 YouTube : https://www.youtube.com/watch?vgkDASVE_Hdg 主要内容是:建立git 库, 保存commit, 建立分支 create branch, 合并分支merge branch,比较 diff,Revert ,history,delete branch, rename branch, t…...
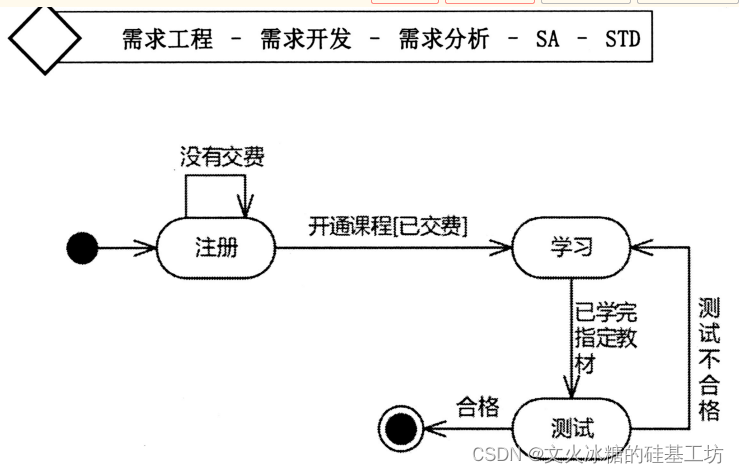
[架构之路-249]:目标系统 - 设计方法 - 软件工程 - 需求工程- 需求开发:如何用图形表达需求,结构化方法的需求分析
目录 一、概述 二、数据模型:E-R图/实体关系图(数据单元之间的结构关系) 三、功能模型:数据流图DFD(逻辑运算,包括输入和输出,实体之间的关系):输入》处理 》 输出 四…...
Django之中间件与CSRF_TOKEN
文章目录 一、什么是中间件二、中间件有什么用三、Django自定义中间件中间件中主要方法及作用创建自定义中间件的步骤:process_request与process_response方法process_view方法process_exceptionprocess_template_response(不常用) 四、CSRF_…...
柑橘病害数据集(四类图像分类,没有打yolo标签)
1.文件夹分为训练集和测试集 在这个数据集中,有一类是新鲜柑橘,还有另外三种疾病,溃疡病、黑斑病和绿化病。 2.train文件夹 2.1.blackspot(黑斑病) 文件夹 206张照片 2.2.canker(溃疡病) 文…...

面向对象三大特性:封装,继承,多态;多态的机制;以及多态是如何实现的,实现的必要条件
文章目录 面向对象三大特性2.1.1 封装 继承 多态2.1.2 其中Java 面向对象编程三大特性:封装 继承 多态2.1.3 关于继承如下 3 点请记住:2.1.4 什么是多态机制?Java语言是如何实现多态的?2.1.5 Java实现多态有三个必要条件ÿ…...

Unity-类-Vector
Vector矢量 是一个基本的数学概念,它允许你描述方向和大小。在游戏和应用中,矢量通常用于描述一些基本属性,如角色的位置、物体移动的速度或两个物体之间的距离。 矢量算术是计算机编程很多方面(如图形、物理和动画)的基础,深入了解这一主题对于充分发挥 Unity 的功能很有…...
【腾讯云云上实验室】向量数据库相亲社交应用实践
快速入口 👉向量数据库_大模型知识库_向量数据存储_向量数据检索- 腾讯云 (tencent.com) 文章目录 前言1. 向量数据库概念及原理1.1 向量数据库概念1.2 向量数据库核心原理1.3 向量数据库优缺点1.4 向量数据库与传统数据库的区别 2. 腾讯云向量数据库的基本特性及优…...

SpringCloud Netflix 知识点汇总
目录 SpringCloud概念:1、什么是springcloud?2、SpringCloud有哪些核心组件?3、什么是分布式?4、什么是微服务?5、分布式+微服务+集群6、微服务之间是如何独立通讯的Eureka1、什么是Eureka ?2、为什么使用Eureka?3、什么是Eureka自我保护机制4、Zookeeper 和 Eureka 区别…...

IO口电压下降那么多是怎么回事??
前几天一个工程师向我反馈他测得如下电路MCU IO口的电压不是3.3V,只有2V多。 IO配置的是输入功能,无上下拉。最初我不太相信这个结果,后来自己用万用表实际测量了下,还真是这个结果 这是咋回事呢?不应该电压就是3.3V吗…...

NLP实践——LLM生成过程中防止重复循环
NLP实践——LLM生成过程中防止重复 1. 准备工作2. 问题分析3. 创建processor3.1 防止重复生成的processor3.2 防止数字无规则循环的processor 4. 使用 本文介绍如何使用LogitsProcessor避免大模型在生成过程中出现重复的问题。 1. 准备工作 首先实例化一个大模型,…...

用苹果签名免费获取Xcode
使用苹果企业签名免费获取Xcode: 打开Xcode。连接iOS设备到Mac。选择Window→Devices and Simulators。选择该设备。将IPA文件拖到“Installed Apps”的列表框中即可安装。使用Cydia Impactor(可以在网上找到相关下载链接): 打开…...
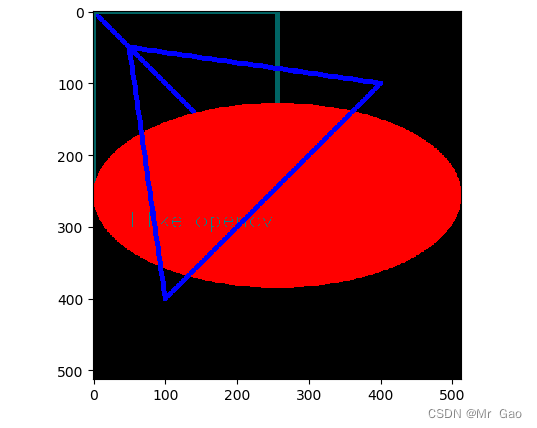
python-opencv在图片中绘制各种图形
python-opencv在图片中绘制各种图形 1.绘制直线 2.绘制矩形 3.绘制圆 4.绘制椭圆 5.绘制多边形 6.嵌入文字 实现代码都在下面了,代码中参数做了简单注释 import copy import math import matplotlib.pyplot as plt import matplotlib as mpl import numpy a…...

用户增长常用的ChatGPT通用提示词模板
用户画像:请帮助我了解目标用户的特点和需求,包括年龄、性别、职业、兴趣等方面的内容,以便我能够更好地定位和推广。 用户获取渠道:请帮助我了解用户主要从哪些渠道获取我们的产品或服务,以便我能够更好地优化获取渠…...
用友NC word.docx接口存在任意文件读取漏洞 附POC
@[toc] 用友NC word.docx接口存在任意文件读取漏洞 附POC 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果及损失,均由使用者本人负责,所产生的一切不良后果与文章作者无关。该文章仅供学习用途使…...
小程序中的大道理之四--单元测试
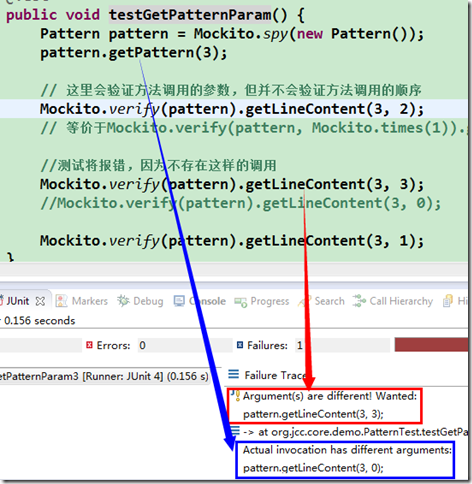
在讨论领域模型之前, 先继续说下关于测试方面的内容, 前面为了集中讨论相应主题而对此作了推迟, 下面先补上关于测试方面的. 测试覆盖(Coverage) 先回到之前的一些步骤上, 假设我们现在写好了 getPattern 方法, 而 getLineContent 还处于 TODO 状态, 如下: public String ge…...
分布式篇---第六篇
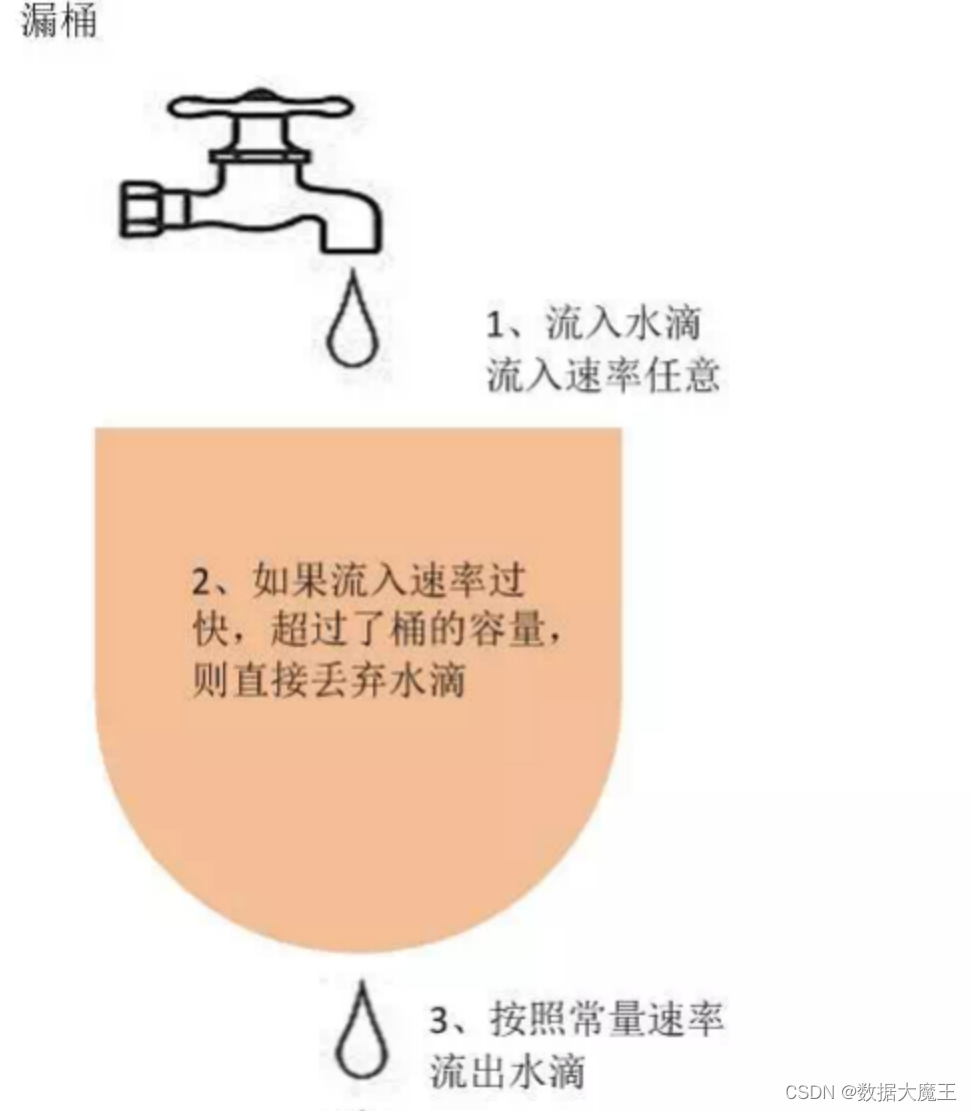
系列文章目录 文章目录 系列文章目录前言一、说说什么是漏桶算法二、说说什么是令牌桶算法三、数据库如何处理海量数据?前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看懂了就去分享给你的码…...
C#,《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码
1 文本格式 /// <summary> /// 《小白学程序》第十八课:随机数(Random)第五,方差及标准方差(标准差)的计算方法与代码 /// 方差 SUM((Xi - X)^2 ) / n i0...n-1 X Average of X[i] ///…...

【版本管理 | Git 】Git最佳实践系列(一) —— LFS .gitignore 最佳实践,确定不来看看?
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

【Linux】驱动程序同步和异步通知方式
一、应用程序APP,访问驱动程序/dev/input/enent1流程: 假设用户程序直接访问 /dev/input/event0 设备节点,或者使用 tslib 访问设备节点,数据的流程如下: APP 发起读操作,若无数据则休眠;用户操…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
