Leetcode算法系列| 1. 两数之和(四种解法)
目录
- 1.题目
- 2.题解
- 解法一:暴力枚举
- 解法二:哈希表解法
- 解法三:双指针(有序状态)
- 解法四:二分查找(有序状态)
1.题目
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
- 示例1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
- 示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
- 示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
- 提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
2.题解
解法一:暴力枚举
最容易想到的方法是枚举数组中的每一个数 x,寻找数组中是否存在 target - x。
当我们使用遍历整个数组的方式寻找 target - x 时,需要注意到每一个位于 x 之前的元素都已经和 x 匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在 x 后面的元素中寻找 target - x。
public int[] TwoSum(int[] nums, int target){int n=nums.Length;for (int i = 0; i < n; i++){for (int j = i + 1; j < n; j++){if (nums[i] + nums[j] == target){return new int[] { i, j };}}}return new int[] { 0, 0 };}

- 时间复杂度: O(n^2) ,空间复杂度: O(1)
解法二:哈希表解法
注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此,我们需要一种更优秀的方法,能够快速寻找数组中是否存在目标元素。如果存在,我们需要找出它的索引。
使用哈希表,可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1)。
这样我们创建一个哈希表,对于每一个 x,我们首先查询哈希表中是否存在 target - x,然后将 x 插入到哈希表中,即可保证不会让 x 和自己匹配。
public int[] TwoSum(int[] nums, int target) {Dictionary<int, int> twoSum = new Dictionary<int, int>();for (int i = 0; i < nums.Length; i++){if(twoSum.ContainsKey(target-nums[i])){return new int[] {twoSum[target - nums[i]], i};}else {twoSum[nums[i]] = i;}}return new int[] {0, 0};}

- 时间复杂度:O(n),空间复杂度:O(n)。
解法三:双指针(有序状态)
public int[] towSum(int[] nums, int target){int left = 0;int right = nums.Length - 1;for (int i = 0; i < nums.Length; i++){if (nums[left] + nums[right] > target){right--;}else if (nums[left] + nums[right] < target){left++;}else{return new int[] { left, right };}}return new int[] { };}
- 时间复杂度:O(nlogn),空间复杂度:O(n)。
解法四:二分查找(有序状态)
public int[] towSum(int[] nums, int target){for (int i = 0; i < nums.Length; i++){int low = i + 1;int high = nums.Length - 1;while (low <= high){int mid = (high - low) / 2 + low;if (nums[mid] > target - nums[i]){high = mid - 1;}else if (nums[mid] < target - nums[i]){low = mid + 1;}else{return new int[] { i, mid };}}}return new int[] { };}
- 时间复杂度:O(nlogn),空间复杂度:O(n)。
相关文章:

Leetcode算法系列| 1. 两数之和(四种解法)
目录 1.题目2.题解解法一:暴力枚举解法二:哈希表解法解法三:双指针(有序状态)解法四:二分查找(有序状态) 1.题目 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数…...

汇编-pop出栈指令
32位汇编 执行动作分为两步: 第一步:读出数据 第二步:改变栈地址 如果操作数是16位, 则ESP加2; 如果操作数是32位, 则ESP加4 espesp2 或 espesp4 格式:...
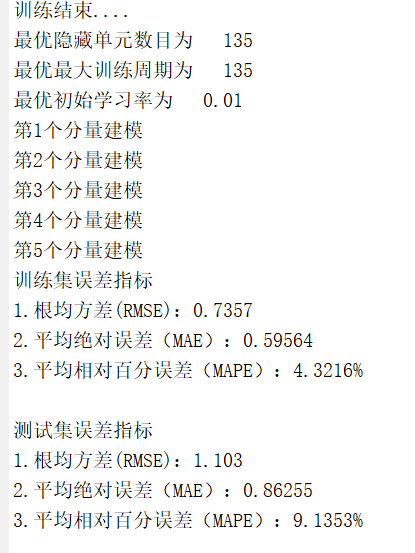
【代码】基于VMD(变分模态分解)-SSA(麻雀搜索算法优化)-LSTM的光伏功率预测模型(完美复现)matlab代码
程序名称:基于VMD(变分模态分解)-SSA(麻雀搜索算法优化)-LSTM的光伏功率预测模型 实现平台:matlab 代码简介:提出了变分模态分解(VMD)和麻雀搜索算法(SSA)与长短期记忆神经网络 (LSTM)相耦合,…...
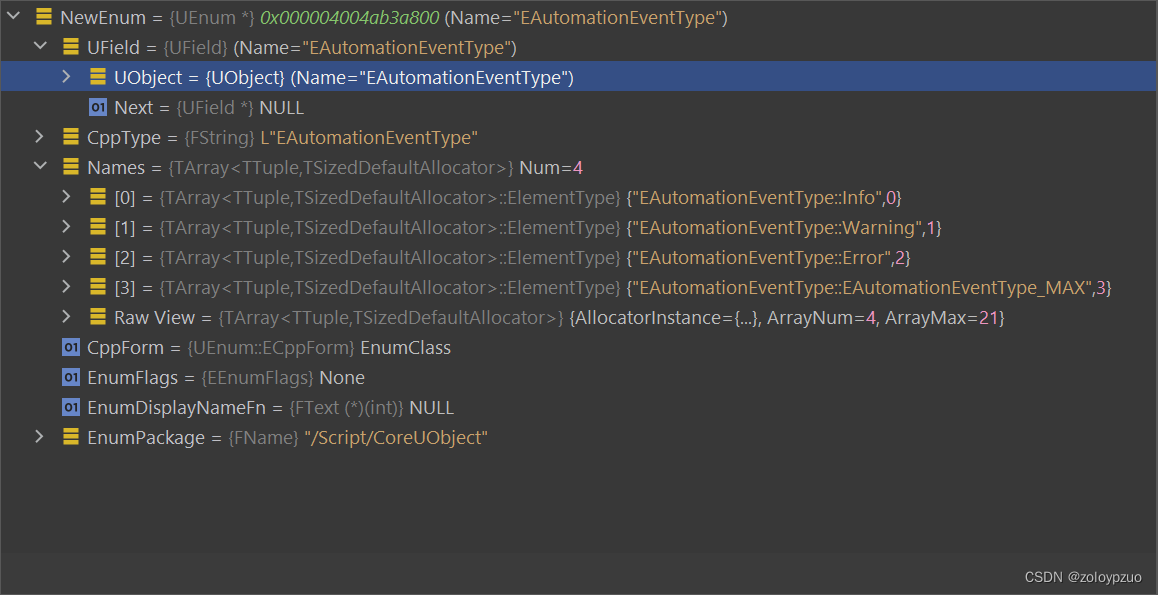
【UnLua】在 Lua 中定义 UE 反射类型
【UnLua】在 Lua 中定义 UE 反射类型 用法 启动编辑器时遍历 Defines 目录下 lua 脚本来加载 UE 反射类型(开个临时的 Lua VM 即可)直接像 -- define a uenum in lua UEnum.EEnumGuestSomethingElse {Value1 1;Value2 2; }-- use it like a native …...
react的开发中关于图片的知识
React是一个流行的JavaScript库,用于构建用户界面。在React开发中,图片是一个非常重要的元素,可以用于美化界面和展示内容。本篇博客将详细讲解React中关于图片的知识。 1. React中使用图片 在React中使用图片非常简单,只需要使…...

AcWing 188:武士风度的牛 ← BFS
【题目来源】https://www.acwing.com/problem/content/190/ 【题目描述】 农民 John 有很多牛,他想交易其中一头被 Don 称为 The Knight 的牛。 这头牛有一个独一无二的超能力,在农场里像 Knight 一样地跳(就是我们熟悉的象棋中马的走法&…...

马养殖场建设VR模拟实训教学平台具有灵活性和复用性
为保障养殖场生物安全,避免疫病传播,学生出入养殖场受时间和地域的限制, 生产实习多以参观为主,通过畜牧企业技术人员的讲解,学生被动了解生产过程。为了解决畜牧养殖实训难的问题,借助VR技术开展畜牧养殖虚…...
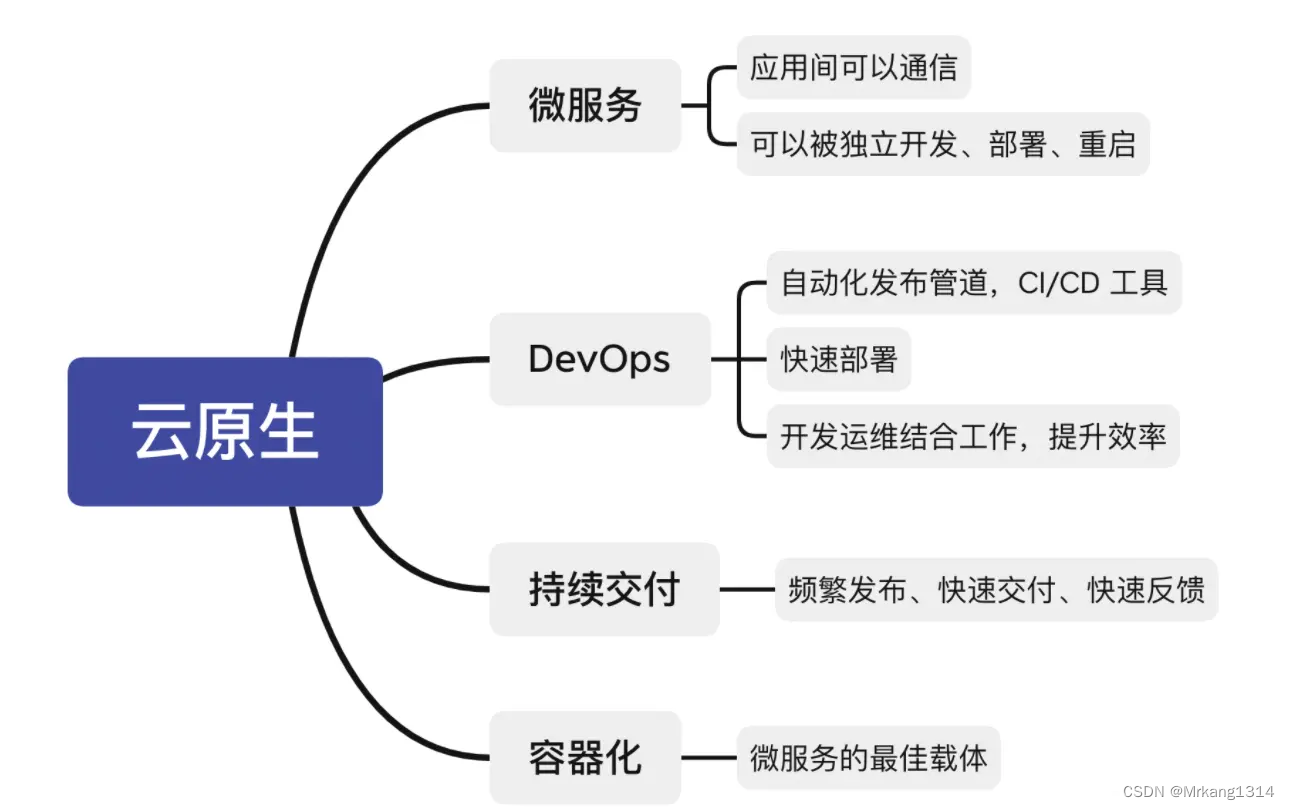
云原生技术演进之路-(云技术如何一步步演进的,云原生解决了什么问题?)
云技术如何一步步演进的? 云原生解决了什么问题? 物理设备 电脑刚被发明的时候,还没有网络,每个电脑(PC),就是一个单机。 这台单机,包括CPU、内存、硬盘、显卡等硬件。用户在单机…...
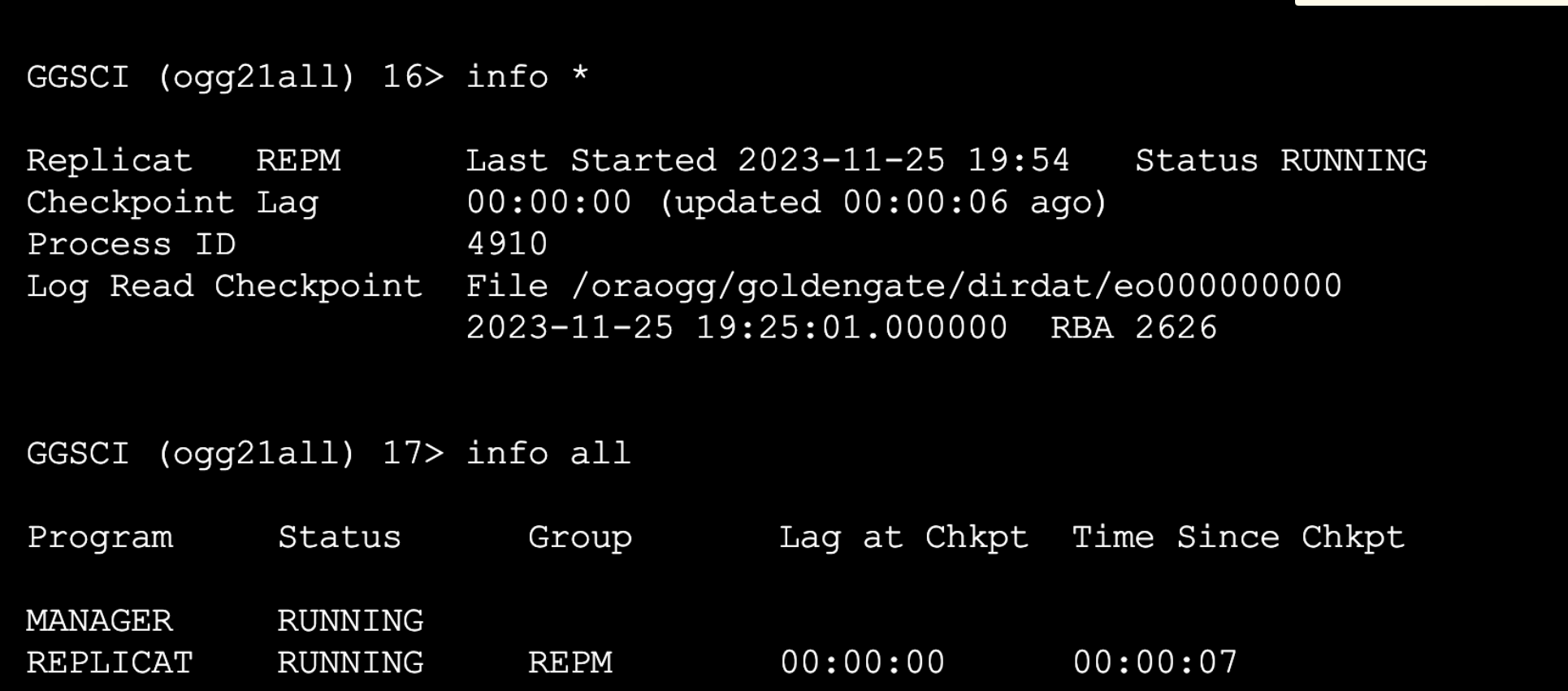
基于OGG实现Oracle实时同步MySQL
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...
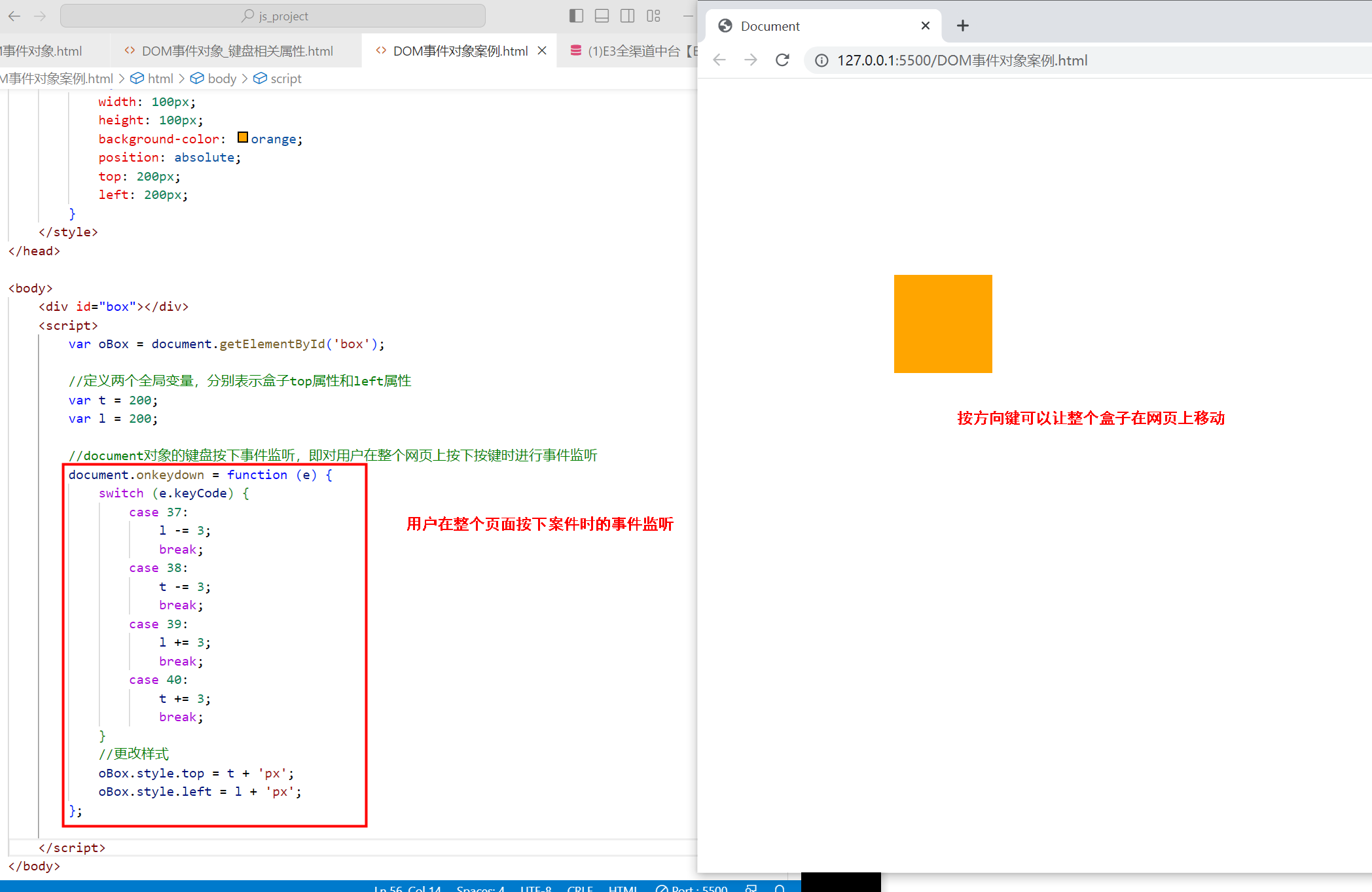
〖大前端 - 基础入门三大核心之JS篇㊷〗- DOM事件对象及它的属性
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:不渴望力量的哈士奇(哈哥),十余年工作经验, 从事过全栈研发、产品经理等工作…...
如何搭建zerotier服务器组网实现内网穿透
小白花了四天的下班时间终于把zerotier网络调通,此刻坐在桌前舒畅地喝口茶~~ 下面来详细记录下这几天踩的坑: 起因就在于一直在iPad上用向日葵连接公司电脑的我觉得向日葵的界面用的实在难受,vs code操作十分不灵光&…...
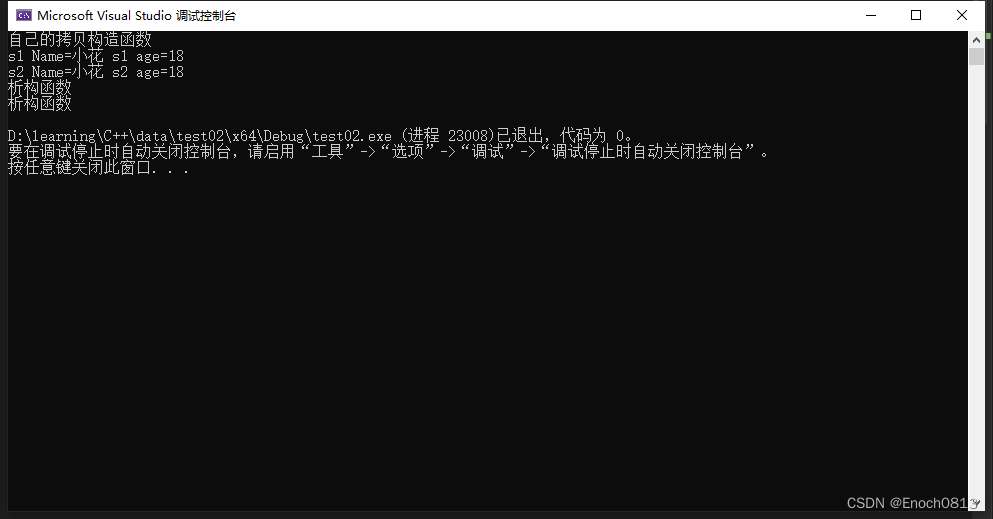
【C++】构造函数和析构函数第四部分(深拷贝和浅拷贝)--- 2023.11.25
目录 什么是浅拷贝?浅拷贝的问题使用深拷贝解决浅拷贝问题结束语 什么是浅拷贝? 如果在一个类中没有人为定义拷贝函数,则系统会提供默认拷贝函数。那么在此默认拷贝函数中主要进行了简单的赋值操作,那这个简单的赋值操作我们一般…...
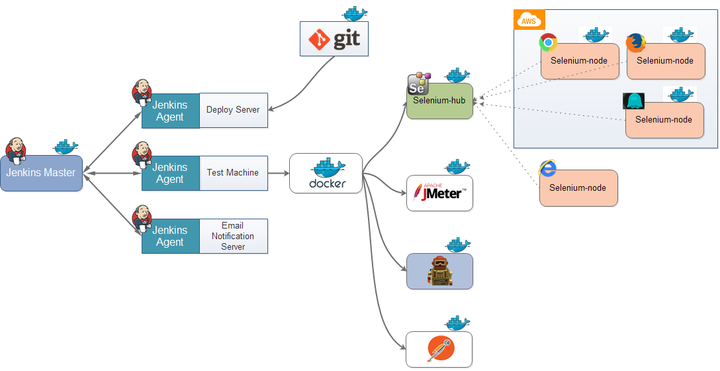
加速软件开发:自动化测试在持续集成中的重要作用!
持续集成的自动化测试 如今互联网软件的开发、测试和发布,已经形成了一套非常标准的流程,最重要的组成部分就是持续集成(Continuous integration,简称CI,目前主要的持续集成系统是Jenkins)。 那么什么是持…...

工具及方法 - 查找排名:国内网络作家排名
中国十大网络小说作家排名,在买购网的排名: 中国十大网络小说作家 网络小说作家排行榜 中国著名网络写手排名→MAIGOO生活榜 (这个网站里还有很多其他的排名。) 1,唐家三少 2,辰东 3,我吃西红…...

MySQL INSERT插入条件判断:如果不存在则插入
MySQL INSERT插入条件判断:如果不存在则插入(转) 我们经常需要进行sql的批量插入,要求:该条记录不存在则插入,存在则不插入。如果使用一条INSERT语句实现呢? ####普通的 INSERT INTO 插入&…...

CSM32RV003:国产高精度16位ADC低功耗RISC-V内核MCU
目录 高精度ADC工业应用工业数据采集应用CSM32RV003简介主要特性 高精度ADC工业应用 高精度ADC即高精度模数转换器,是一种能够将输入模拟信号转换为数字信号的芯片,在多种消费电子、工业、医疗和科研领域都有广泛应用。高精度ADC的主要特点是能够提供高…...

65道常问前端面试题总结react
面试题总结 一.Axios的实现原理 Axios 是一个基于 Promise 的 HTTP 客户端库,用于浏览器和 Node.js 环境。它可以发送 HTTP 请求并处理响应数据。下面是 Axios 实现的基本原理: 封装请求:Axios 提供了一个简单易用的 API,使得开…...
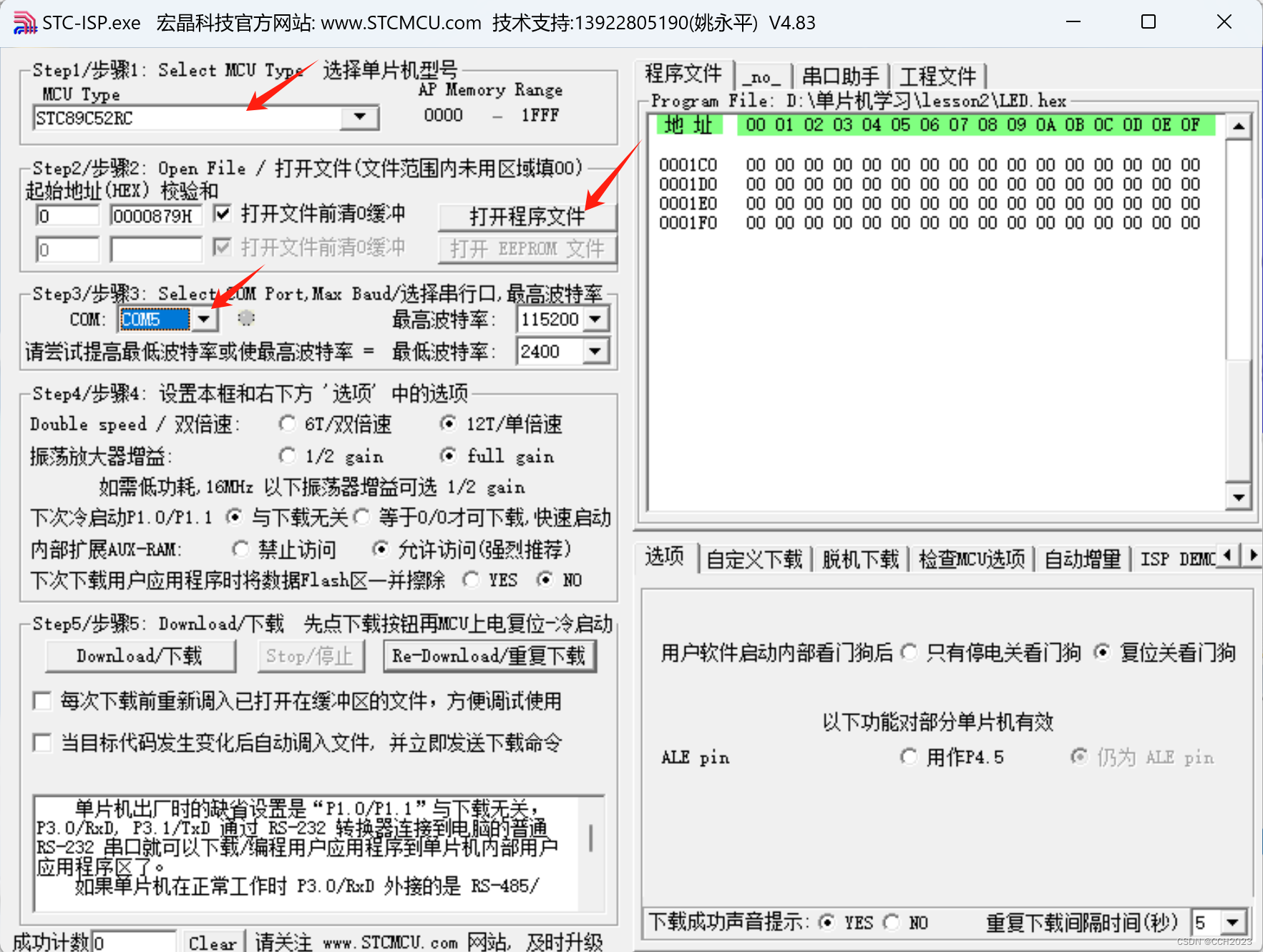
单片机学习1——点亮一个LED灯
Keil软件编写程序: 特殊功能寄存器声明: #include<reg52.h>sbit LED P1^0;void main() {LED 0;while(1); } 代码说明: sbit 语句是特殊功能位声明。 生成HEX文件,这个文件是下载到单片机里的文件。Options for Target…...
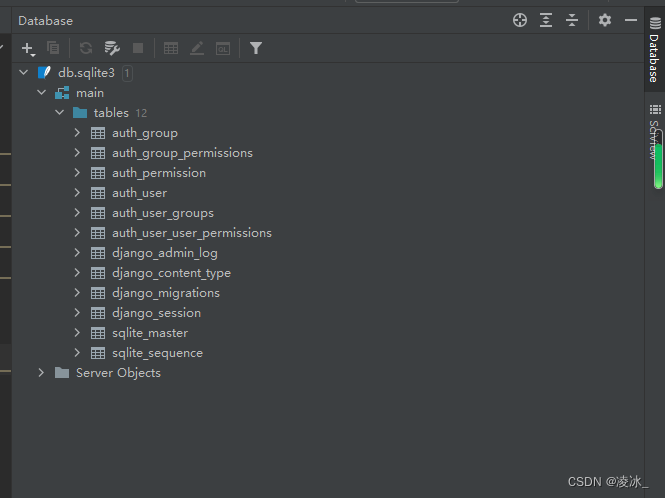
PyCharm 配置sqlite3驱动下载问题
单击View -> Tool Windows -> Database,打开Database窗体,之后进行配置,下载驱动包失败! 解决 (1)下载Sqlite3驱动 下载地址: Central Repository: org/xerial/sqlite-jdbc 选择的版本是3.34.0,下载…...

NVMe-oF E-JBOF设计解析:WD RapidFlex网卡、OpenFlex Data24
OpenFlex Data24 NVMe-oF Storage Platform WD的SN840 NVMeSSD新品并没有太吸引我注意,因为它还是PCIe 3.0接口的,要知道Intel的PCIe 4.0 SSD都已经推出了。 但上面这个NVMe-oF(NVMe over Fabric)EBOF(区别于普通JBO…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
