153、【动态规划】leetcode ——416. 分割等和子集:滚动数组(C++版本)
题目描述
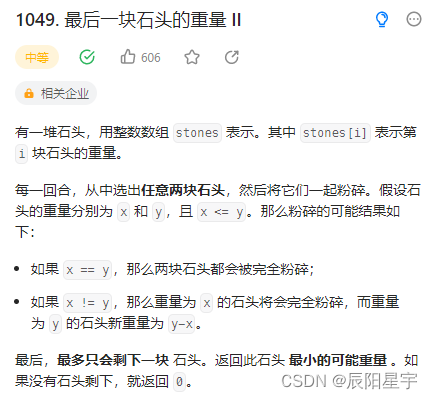
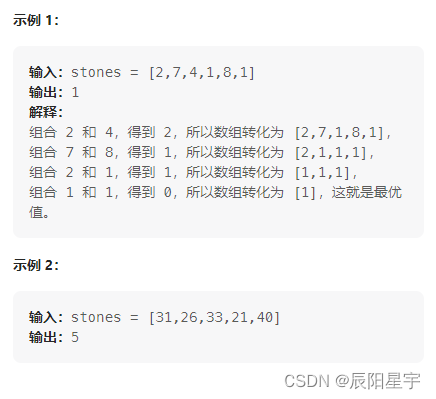

原题链接:1049. 最后一块石头的重量 II
解题思路
本题要找的是最小重量,我们可以将石头划分成两个集合,当两个集合的重量越接近时,相减后,可达到的装量就会是最小,此时本题的思路其实就类似于 416. 分割等和子集(动态规划:二维数组+滚动数组) 。
首先,对所有石头的总重量求和,然后设置一个变量target表示总重量之和的二分之一,使用动态规划的方式,划分出一个集合之和dp[target],然后用总重量之和减去dp[target],就得到对石头的另一个集合划分之和。二者相减,就是最小重量。
- 动态规划五步曲:
(1)dp[j]含义: 在背包容量为j的条件下,可装入的最大物品重量总和。
(2)递推公式: dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sumNums = 0;for(int i = 0; i < stones.size(); i++) sumNums += stones[i];int target = sumNums / 2;int dp[1501] = {0};int n = stones.size();for(int i = 0; i < n; i++) {for(int j = target; j >= stones[i]; j--) {dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);}}return abs(sumNums - dp[target] - dp[target]);}
};
参考文章:1049. 最后一块石头的重量 II
相关文章:

153、【动态规划】leetcode ——416. 分割等和子集:滚动数组(C++版本)
题目描述 原题链接:1049. 最后一块石头的重量 II 解题思路 本题要找的是最小重量,我们可以将石头划分成两个集合,当两个集合的重量越接近时,相减后,可达到的装量就会是最小,此时本题的思路其实就类似于 4…...
linux head命令(head指令)(获取文件或管道输出结果前n行,默认前10行)与sed命令区别
head命令是一个在Linux系统中常用的命令,用于读取文件的前几行(默认读取前10行) 文章目录使用方法读取文件的前10行:head filename读取文件的前n行:head -n行数 filename读取多个文件的前几行:head -n 行数…...
Mysql数据库09——分组聚合函数
类似pandas里面的groupby函数,SQL里面的GROUP BY子句也是可以达到分组聚合的效果。 常用的聚合函数有COUNT(),SUM(),AVG(),MAX(),MIN(),其用法看名字都看的出来,下面一一介绍 聚合函数 COUNT()计数 统计student表中计科系学生的人数。 SE…...

第43章 菜单实体及其约束规则的定义实现
1 Core.Domain.Security.Menu namespace Core.Domain.Security { /// <summary> /// 【菜单--类】 /// <remarks> /// 摘要: /// 通过该实体类及其属性成员,用于实现当前程序【Core】.【领域】.【安全】.【菜单】实体与“[ShopDemo].[…...

OpenAI最重要的模型【CLIP】
最近的 AI 突破 DALLE和 Stable Diffusion有什么共同点? 它们都使用 CLIP 架构的组件。 因此,如果你想掌握这些模型是如何工作的,了解 CLIP 是先决条件。 此外,CLIP 已被用于在 Unsplash 上索引照片。 但是 CLIP 做了什么&…...

分享112个JS菜单导航,总有一款适合您
分享112个JS菜单导航,总有一款适合您 112个JS菜单导航下载链接:https://pan.baidu.com/s/1Dm73d2snbu15hZErJjTXxg?pwdfz1c 提取码:fz1c Python采集代码下载链接:https://wwgn.lanzoul.com/iKGwb0kye3wj base_url "h…...
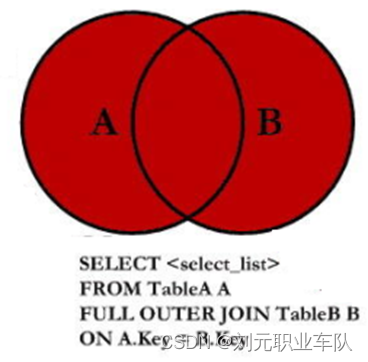
MySQL 3:MySQL数据库基本操作 DQL
数据库管理系统的一个重要功能是数据查询。数据查询不应简单地返回数据库中存储的数据,还应根据需要对数据进行过滤,确定数据的显示格式。MySQL 提供了强大而灵活的语句来实现这些操作。MySQL数据库使用select语句查询数据。 select [all|distinct]<…...

sql语句的优化
sql优化 优化数据访问 查询性能低下最基本的原因是访问的数据太多,大部分性能低下的查询都可以通过减少访问的数据量来优化所以关于低效的查询,需要确认是否检索了大量不需要的数据,以及mysql服务器层是否在分析大量不需要的数据 因为有些查…...

Shell脚本之——自动安装JDK
目录 1.修改主机名 2.创建文件,单独存放Shell脚本 3.编写Shell脚本 4.Shell脚本命令简介 (1)文件头 (2)打印命令 (3)设置全局变量 (4)条件判断 (5)解压 (6)文件重命名 (7)在/etc/profile指定行插入 5.完整脚本内容 6.重启环境变量 7.判断java是否配置…...
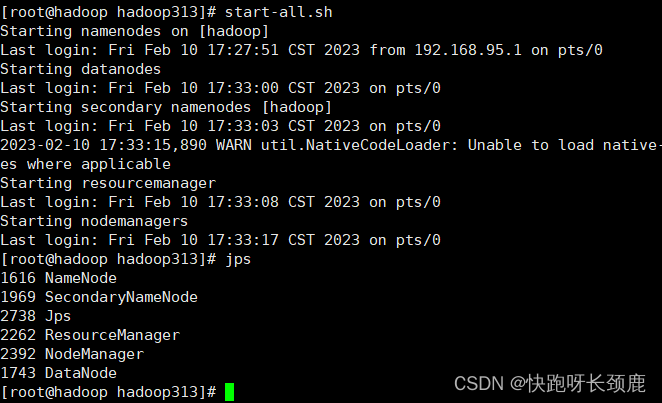
大数据---Hadoop安装Hadoop简易版
编写自动安装Hadoop的shell脚本 完整流程: 大数据—Hadoop安装教程(二) 文章目录编写自动安装Hadoop的shell脚本上传压缩包编写shell脚本vim hadoopautoinstall.sh运行上传压缩包 在opt目录下创建连个目录install和soft 将压缩包上传到install目录下 …...
)
Spring框架中使用到的设计模式以及对应的类(方法)
模板方法--->postProcessBeanFactory,onFresh、initPropertySource装饰器模式--->BeanWrapper委托者模式--->BeanDefinitionParseDelegate策略模式--->ClassPathXmlApplicationContext、FileSystemApplicationContext、XMLBeanDefinitionReader、Proper…...

类和类的定义
6.2 类和类的定义 面向对象最重要的概念就是类(Class)和实例(Instance),必须牢记类是抽象的模板,比如学生类,而实例是根据类创建出来的一个个具体的对象,每个对象都拥有相同的方法&…...

丝绸之路——NFT 系列来袭!
丝绸之路的经历讲述了汉朝时代的一个重要历史事件。该系列中的 NFT 带有中国这段黄金时代令人愉悦的视觉元素,使其成为值得收藏的物品。 NFT 系列介绍 敦煌女神像01(左);汉代士兵(中);敦煌女神像…...

配置CMAKE编译环境:VSCODE + MinGW
一. MinGW安装 MinGW(Minimalist GNU For Windows)是个精简的Windows平台C/C、ADA及Fortran编译器,相比Cygwin而言,体积要小很多,使用较为方便。 MinGW最大的特点就是编译出来的可执行文件能够独立在Windows上运行。 MinGW的组成ÿ…...
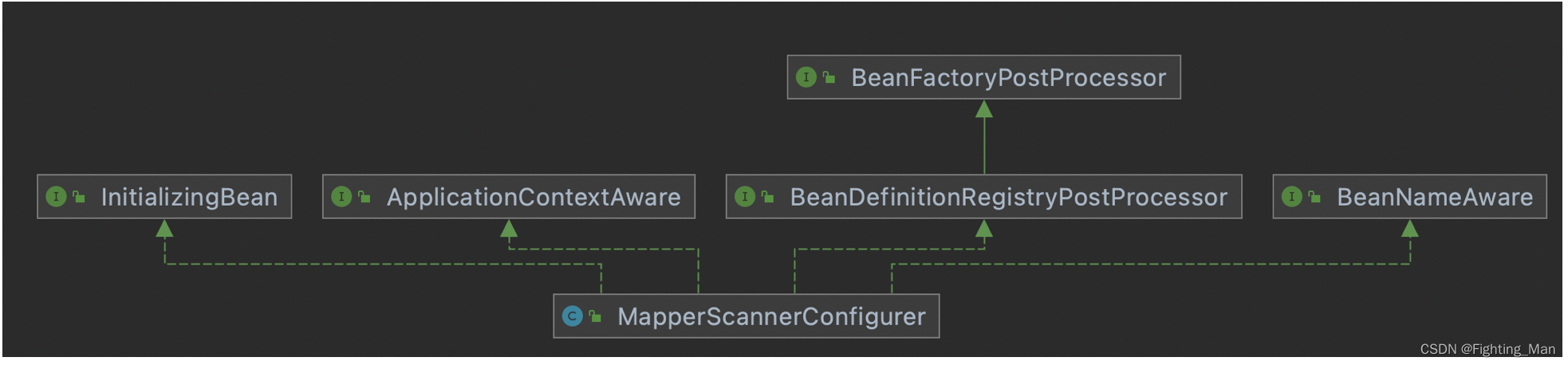
六、mybatis与spring的整合
Spring整合Mybaits的步骤 引入依赖 在Spring整合Mybaits的时候需要引入一个中间依赖包mybatis-spring <dependency><groupId>org.mybatis</groupId><artifactId>mybatis</artifactId><version>3.5.5</version> </dependency&g…...
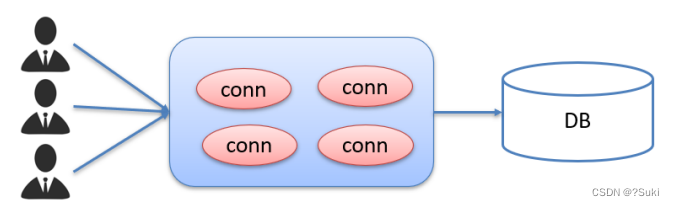
JavaWeb--JDBC
JDBC1 JDBC概述1.1 JDBC概念1.2 JDBC本质1.3 JDBC好处2 JDBC快速入门2.1 编写代码步骤2.2 具体操作3 JDBC API详解3.1 DriverManager3.2 Connection3.2.1 获取执行对象3.2.2 事务管理3.3 Statement3.3.1 概述3.3.2 代码实现3.4 ResultSet3.4.1 概述3.4.2 代码实现3.5 案例3.6 P…...

大数据框架之Hadoop:入门(四)Hadoop运行模式
Hadoop运行模式包括:本地模式、伪分布式模式以及完全分布式模式。 Hadoop官方网站:http://hadoop.apache.org/ 4.1本地运行模式 4.1.1官方Grep案例 1.创建在hadoop文件夹下面创建一个input文件夹 [roothdp101 hadoop]# mkdir input2.将Hadoop的xml配…...
《爆肝整理》保姆级系列教程python接口自动化(十一)--发送post【data】(详解
简介 前面登录的是传 json 参数,由于其登录机制的改变没办法演示,然而在工作中有些登录不是传 json 的,如 jenkins 的登录,这里小编就以jenkins 登录为案例,传 data 参数,给各位童鞋详细演练一下。 一、…...

【微服务】Nacos注册中心
🚩本文已收录至专栏:微服务探索之旅 👍希望您能有所收获 👍Nacos和Eureka一样也可以充当服务的注册中心,让我们一起看看有何区别? 点击跳转👉【微服务】Eureka注册中心 👍Nacos除了可…...

跟开发打了半个月后,我终于get报bug的正确姿势了
在测试人员提需求的时候,大家经常会看到,测试员和开发一言不合就上BUG。然后开发一下就炸了,屡试不爽,招招致命。 曾经看到有个段子这么写道: 不要对程序员说,你的代码有BUG。他的第一反应是:…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
