用HALCON标定助手对相机进行标定
任务要求:
已知相机镜头焦距f为8mm,相机单个CCD像素在水平和竖直两个方向上的尺寸均为3.75微米,相机为普通透光镜头和面阵相机,对相机进行标定,测量相机的内外参数。
操作步骤:
1. 在HALCON中运行gen_caltab算子,生成标定板和标定描述文件。
gen_caltab( : : XNum, YNum, MarkDist, DiameterRatio, CalPlateDescr, CalPlatePSFile : )。其中参数含义:
XNum, Ynum:标定板上水平、垂直方面的标志点数量;
MarkDist:标志点之间距离;
DiameterRatio:标志点直径占标志点距离的比例;
CalPlateDescr:标定板描述文件;
CalPlatePSFile:标定板图像文件。
2. 在PhotoShop软件中打开caltab.ps文件,并打印输出。
3. 打开标定助手,在“安装”页面中选择“全标定”,即对内外参数进行标定;在“描述文件”对话框中输入描述文件路径;输入摄像机模型“面扫描”;设置单个像元的高和宽;设置焦距。

4. 打开“标定”页面,在“图像源”下可以选择“图像文件”,选择标定板照片;或者选择“图像采集助手”,通过摄像机实时采集标定板照片。完成20张图像采集后,点击标定。
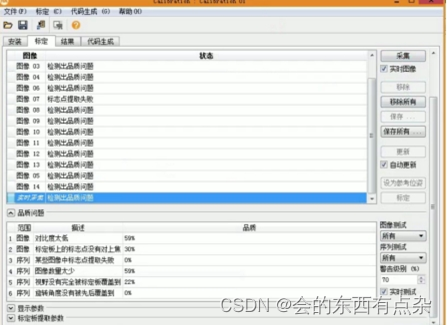
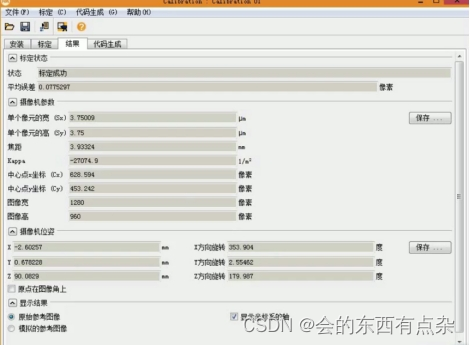
5.点击“结果”,弹出结果页面。“摄像机参数”为相机的内参,“摄像机位姿”为相机的外参。点击“保存”按钮,保存摄像机的内外参数。
相关文章:

用HALCON标定助手对相机进行标定
任务要求: 已知相机镜头焦距f为8mm,相机单个CCD像素在水平和竖直两个方向上的尺寸均为3.75微米,相机为普通透光镜头和面阵相机,对相机进行标定,测量相机的内外参数。 操作步骤: 1. 在HALCON中运行gen_ca…...

5 个适用于 Windows 的顶级免费数据恢复软件
对于计算机来说,最重要的是用户数据。除了您的数据之外,有关计算机的其他所有内容都是可替换的。这三个是数据丢失的最常见原因: 文件/文件夹删除丢失分区分区损坏 文件/文件夹删除 文件/文件夹删除是最常见的数据丢失类型。大多数时候&am…...

MySQL 批量插入记录报 Error 1390 (HY000)
文章目录 1.背景2.问题3.分批插入4.一次最多能插入多少条记录?5.什么是 Prepared Statement?参考文献 1.背景 Golang 后台服务使用 GORM 实现与 MySQL 的交互,在实现一个通过 Excel 导入数据的接口时,使用 Save 方法一次性插入大…...
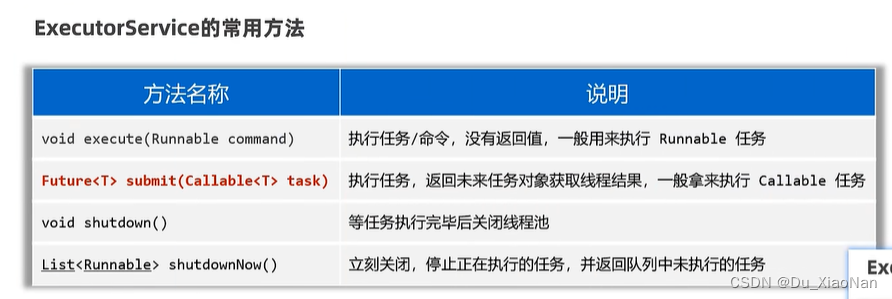
线程池(用于处理Runnable任务或Callable任务)
一,线程池 二, 如何创建线程池 案例: //1,通过ThreadPoolExecuter创建一个线程池对象ExecutorService pool new ThreadPoolExecutor(3,5,8,TimeUnit.SECONDS,new LinkedBlockingQueue<>(4),Executors.defaultThreadFactory(),new Thr…...
MATLAB在信号系统中的应用
1.产生一个幅度为1, 基频为2Hz,占空比为50%的周期方波.要求画出图形。 在MATLAB中,函数square(w0*t, DUTY)产生基本频率为w0 (周期T2*pi/w0)、占空比DUTY (τ/T)*100的周期矩形波(方波),默认情况下占空比DUTY50。占空…...
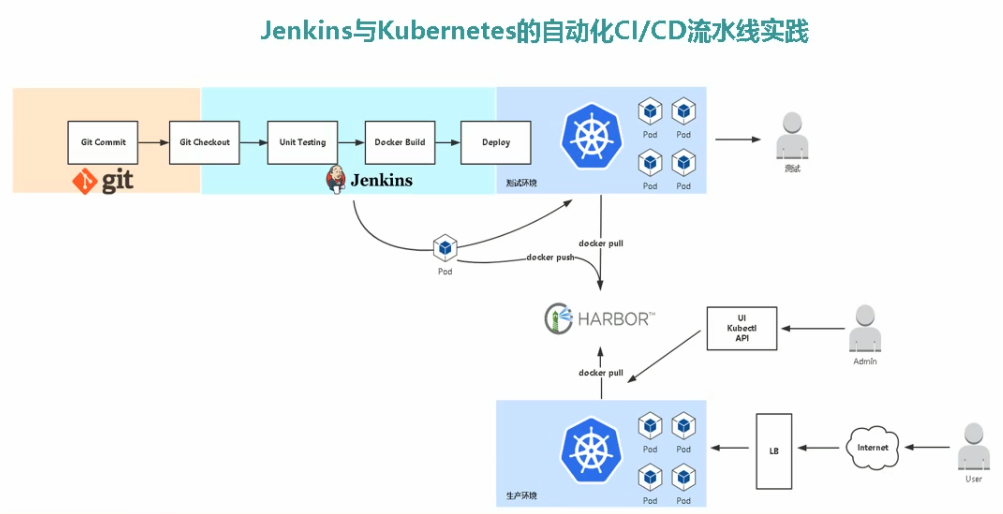
Jenkins与Docker的自动化CI/CD流水线实践
Pipeline 有诸多优点,例如: 项目发布可视化,明确阶段,方便处理问题 一个Jenkins File文件管理整个项目生命周期 Jenkins File可以放到项目代码中版本管理 Jenkins管理界面 操作实例:Pipeline的简单使用 这里是比较…...

企业数字化转型的作用是什么?_光点科技
在当今快速变化的商业环境中,数字化转型已成为企业发展的重要策略。企业数字化转型指的是利用数字技术改造传统业务模式和管理方式,以提升效率、增强竞争力和创造新的增长机会。 提升运营效率:数字化转型通过引入自动化工具和智能系统&#x…...

css加载会造成阻塞吗??
前言 前几天面试问到了这个问题,当时这个答得不敢确定哈哈,虽然一面还是过了 现在再分析下这个,总结下,等下次遇到就能自信得回答,666 准备工作 为了完成本次测试,先来科普一下,如何利用chr…...
——第16期)
Java中的jvm——面试题+答案(JVM的高级概念和调优技巧,包括垃圾回收、内存分析、优化技术等)——第16期
涉及Java虚拟机(JVM)高级概念和调优技巧的面试题以及简要答案: 什么是JVM调优?有哪些常见的JVM调优参数? 答案: JVM调优是通过调整JVM的参数和配置,以提高Java应用程序的性能和稳定性。常见的JV…...

***Linux下Mysql的安装
以下是在Linux系统下安装MySQL的步骤: 1.访问MySQL官网下载页面(https://dev.mysql.com/downloads/mysql/),选择适合您Linux系统的版本进行下载。 2.下载完成后,解压缩文件并将其移动到/usr/local目录下:…...

Linux踩坑:arm下gcc编译添加 -Ox 优化后,程序无法正常运行
arm下gcc编译添加 -Ox 优化后,程序无法正常运行 一、问题描述 今天学习正点原子的阿尔法开发板裸机开发的时候,遇到了一个问题,在没有使用 -Ox 优化的时候,编译出来的程序能够正常运行,但是添加了-Ox之后,…...

Vue3中Composition API介绍
在Vue 3中,引入了Composition API,它是一种新的组合式函数API,用于更灵活地组织和重用组件逻辑。Composition API相比于Vue 2中的Options API,提供了更好的可组合性和代码复用性。下面是对Vue 3中Composition API的介绍和用法&…...
Centos7下搭建Android开发环境及Android真机调试)
虚拟机系列:(VMware Workstation Pro)Centos7下搭建Android开发环境及Android真机调试
一、Android SDK 安装配置 1、环境 Linux系统为:Red Hat Enterprise Linux 7 64 位 ; 当然还需要Java环境,java 环境这里不叙述; 2、Android Studio 安装 (1)下载位置: http://www.android-studio.org/ 我这里下载的:android-studio-ide-191.5977832-linux.tar.gz …...
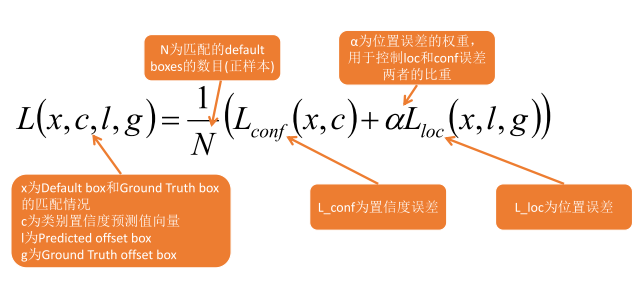
全面(16万字)深入探索深度学习:基础原理到经典模型网络的全面解析
前言 Stacking(堆叠) 网页调试 学习率:它决定了模型在每一次迭代中更新参数的幅度激活函数-更加详细 激活函数的意义: 激活函数主要是让模型具有非线性数据拟合的能力,也就是能够对非线性数据进行分割/建模 如果没有激活函数: 第一个隐层: l…...
openEuler Linux 部署 FineBi
openEuler Linux 部署 FineBi 部署环境 环境版本openEuler Linux22.03MySQL8.0.35JDK1.8FineBi6.0 环境准备 升级系统内核和软件 yum -y updatereboot安装常用工具软件 yum -y install vim tar net-tools 安装MySQL8 将 MySQL Yum 存储库添加到系统的存储库列表中 sudo…...

QThreadStorage使用介绍
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 什么是线程数据存储Qt中的线程数据存储`QThreadStorage` 的用法:代码示例什么是线程数据存储 线程数据存储是指为每个线程在程序中分配和管理数据的过程。它主要用于并发编程…...

AI和人工智能与机器学习全景报告
今天分享的是AI系列深度研究报告:《AI和人工智能与机器学习全景报告》。 (报告出品方:appen) 报告共计:30页 获取 数据获取仍是AI应用构建团队的主要瓶颈。 原因各不相同。例如,特定用例的数据可能不足…...

【计算机网络】(网络层)定长掩码和变长掩码
目录 1、IPV4地址的应用规划 2、例题分析 2.1、定长的子网掩码 2.2、变长的子网掩码 1、IPV4地址的应用规划 定长的子网掩码(FLSM): 使用同一个子网掩码划分子网,每个子网所分配的IP地址数量相同,造成IP地址的浪费…...
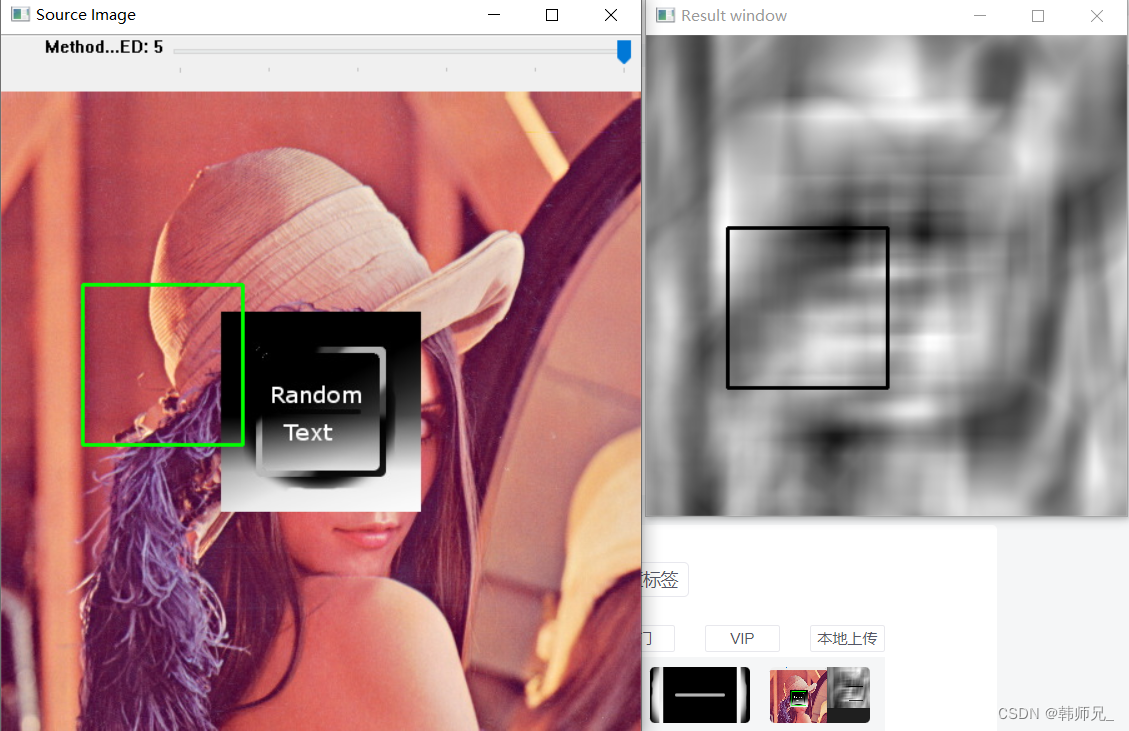
008 OpenCV matchTemplate 模板匹配
目录 一、环境 二、模板匹配算法原理 三、代码演示 一、环境 本文使用环境为: Windows10Python 3.9.17opencv-python 4.8.0.74 二、模板匹配算法原理 cv.matchTemplate是OpenCV库中的一个函数,用于在图像中查找与模板匹配的特征。它的主要应用场景…...

PTA 海盗分赃
P 个海盗偷了 D 颗钻石后来到公海分赃,一致同意如下分赃策略: 首先,P 个海盗通过抽签决定 1 - P 的序号。然后由第 1 号海盗提出一个分配方案(方案应给出每个海盗分得的具体数量),如果能够得到包括 1 号在…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
