[DFS深度优先搜索]集合里的乘法
集合里的乘法
题目描述
给定一个目标数T和一个整数集合S,判断是否存在S的一个非空子集,子集中的数相乘的积为T。
关于输入
输入为两行。
第一行为目标数T,和S中的元素个数N,以空格隔开。
第二行为S中的N个元素,以空格隔开。
其中 N <= 16。
关于输出
如果可以,则输出YES,否则输出NO。
例子输入
12 5 1 2 3 4 5
例子输出
YES
解题分析
这个算法的核心思想是使用深度优先搜索(DFS)遍历所有可能的子集,并计算它们的乘积。如果找到一个子集的乘积等于目标数,就返回YES,否则返回NO。
以下是该算法的详细步骤:
1. 首先,我们读取目标数T和集合S的元素。集合S的元素被存储在一个数组中,数组的索引从0开始。
2. 然后,我们调用深度优先搜索函数`dfs`,开始时的索引为0,乘积为1。这意味着我们从集合的第一个元素开始搜索,初始的乘积是1(因为任何数乘以1都等于它自己)。
3. 在`dfs`函数中,我们首先检查是否已经找到了解决方案(`flag`是否为1)或者当前乘积是否已经超过了目标数T。如果是的话,我们就直接返回,不再继续搜索。这是一种剪枝策略,可以避免无效的搜索,提高算法的效率。
4. 然后,我们检查当前的乘积是否等于目标数,如果是的话,我们就设置`flag`为1并返回。这表示我们已经找到了一个满足条件的子集。
5. 如果当前的索引已经达到了集合的大小,这意味着我们已经遍历了所有的元素,但还没有找到满足条件的子集,所以我们就返回。
6. 否则,我们对当前索引的元素有两种选择:一是选择它(将它乘入当前的乘积),二是不选择它(保持当前的乘积不变)。我们对这两种选择都进行搜索。这是深度优先搜索的核心步骤,通过递归调用`dfs`函数,我们可以遍历所有可能的子集。
7. 在主函数中,如果`flag`为1,说明我们找到了一个解决方案,输出YES。否则,输出NO。
这个算法的时间复杂度是O(2^n),其中n是集合的大小。因为对于集合中的每一个元素,我们都有两种选择:选择它或者不选择它。所以总共有2^n种可能的子集。由于题目中给出集合的大小不超过16,所以这个算法在时间上是可行的。
代码实现
#include <stdio.h>int N;
long long T, S[16];
char flag;void dfs(int index, long long product) {if (flag || product > T) return;if (product == T) {flag = 1;return;}if (index == N) return;dfs(index + 1, product * S[index]);dfs(index + 1, product);
}int main() {scanf("%lld %d", &T, &N);for (int i = 0; i < N; i++) {scanf("%lld", &S[i]);}dfs(0, 1);if (flag) {printf("YES\n");} else {printf("NO\n");}return 0;
}
相关文章:

[DFS深度优先搜索]集合里的乘法
集合里的乘法 题目描述 给定一个目标数T和一个整数集合S,判断是否存在S的一个非空子集,子集中的数相乘的积为T。 关于输入 输入为两行。 第一行为目标数T,和S中的元素个数N,以空格隔开。 第二行为S中的N个元素,以空…...
K8s 中 Pod OOMKilled 原因
目录 Exit Code 137 解决方案 JVM 感知 cgroup 限制 使用 JDK9 的容器感知机制尝试 问题分析 容器内部感知 CGroup 资源限制 在 Java10 中,改进了容器集成 JVM 参数 MaxDirectMemorySize -XX:MaxDirectMemorySize 的默认值是什么? 其他获取 ma…...

为什么程序员最应该学习的是运营与销售,而不是技术?
大概几个月前,我加入了某副业交流群。这里人才很多,不光是传统意义上的程序员,也有公司老板、偏门大佬、产品经理等。 群里的聊天主题就是搞钱俩字,大家讨论着如何搞钱,分享每日收益情况,以及自己做的产品等…...
多表连接)
MySql数据库常用指令(五)多表连接
MySql数据库常用指令(五)多表连接 一、内连接,或等值连接二、左连接三、右连接 实际应用中,我们常常要连接几个不同的MySQL表,因此在 SELECT, UPDATE 和 DELETE 语句中使用 Mysql 的 JOIN 来联合多表查询 INNER JOIN(内…...

Centos7使用rpm安装mysql 5.7.43
Centos7使用rpm安装mysql 5.7.43 1、下载rpm包 wget https://downloads.mysql.com/archives/get/p/23/file/mysql-5.7.43-1.el7.x86_64.rpm-bundle.tar2、解压并安装 tar xf mysql-5.7.43-1.el7.x86_64.rpm-bundle.tar yum -y install mysql-*3、按需修改mysql配置 #注意&a…...
补充:如何提高selenium的运行速度?
已经通读该专栏文章的同学,或许对UI自动化测试有了一定的掌握,细心的同学肯定会发现一个问题,当用例量达到一定程度时,对于整体用例的执行速度肯定不会很满意。除了应用多线程运行用例的方式加快速度,有没有其他的方法呢? 今天告诉大家,方法是有的!也是本人新学的。即…...

使用Python+Redis实现文章投票网站后端功能
1.实现投票功能,2.创建文章数据,3.对文章进行排序。 实现投票功能 实现投票功能,要注重文章的时效性与投票的公平性,所以需要给投票功能加上一些约束条件: 文章发布满一个星期后&…...

SpringBoot 环境使用 Redis + AOP + 自定义注解实现接口幂等性
目录 一、前言二、主流实现方案介绍2.1、前端按钮做加载状态限制(必备)2.2、客户端使用唯一标识符2.3、服务端通过检测请求参数进行幂等校验(本文使用) 三、代码实现3.1、POM3.2、application.yml3.3、Redis配置类3.4、自定义注解…...
Leetcode—18.四数之和【中等】
2023每日刷题(四十一) Leetcode—18.四数之和 实现代码 class Solution { public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ans;sort(nums.begin(), nums.end());int n …...

springsecurity6配置二
一、springsecurity6自定义认证异常处理器 1.1 AuthenticationEntryPointImpl.java package com.school.information.core.security.handler;import com.alibaba.fastjson.JSON; import com.school.information.enums.result.ResultStatusEnum; import com.school.informatio…...
)
php如何对比浮点数大小(bccomp函数)
第一部分,常规例子: 例1:左边比右边小,结果:-1 //示例,左边比右边小返回值:-1 $price1 2.14; $price2 3.14; $result bccomp($price1, $price2, 2); echo 对比结果:.$result;//…...
服务号和订阅号哪个好
服务号和订阅号有什么区别?服务号转为订阅号有哪些作用?在推送频率上来看,服务号每月能推送四条消息,而订阅号可以每天(24小时)推送一条消息。如果企业开通公众号的目的是提供服务,例如售前资讯…...

面试问题--智能指针
什么是智能指针? 当你在编写程序时,可能需要在运行时动态分配内存来存储数据。在传统的C中,你可能会使用 new 和 delete 操作符来手动管理内存。但是这样容易出现一些问题,比如忘记释放内存导致内存泄漏,或者释放了之…...
向量机SVM原理理解和实战
目录 概念场景导入 点到超平面的距离公式 最大间隔的优化模型 硬间隔、软间隔和非线性 SVM 用 SVM 如何解决多分类问题 1. 一对多法 2. 一对一法 SVM主要原理和特点 原理 优点 缺点 支持向量机模型分类 SVM实战如何进行乳腺癌检测 数据集 字段含义 代码实现 参…...

什么是 Node.js?
在 Node.js 出现之前,最常见的 JavaScript 运行时环境是浏览器,也叫做 JavaScript 的宿主环境。浏览器为 JavaScript 提供了 DOM API,能够让 JavaScript 操作浏览器环境(JS 环境)。 2009 年初 Node.js 出现了…...
系列九、声明式事务(xml方式)
一、概述 声明式事务(declarative transaction management)是Spring提供的对程序事务管理的一种方式,Spring的声明式事务顾名思义就是采用声明的方式来处理事务。这里所说的声明,是指在配置文件中声明,用在Spring配置文件中声明式的处理事务来…...
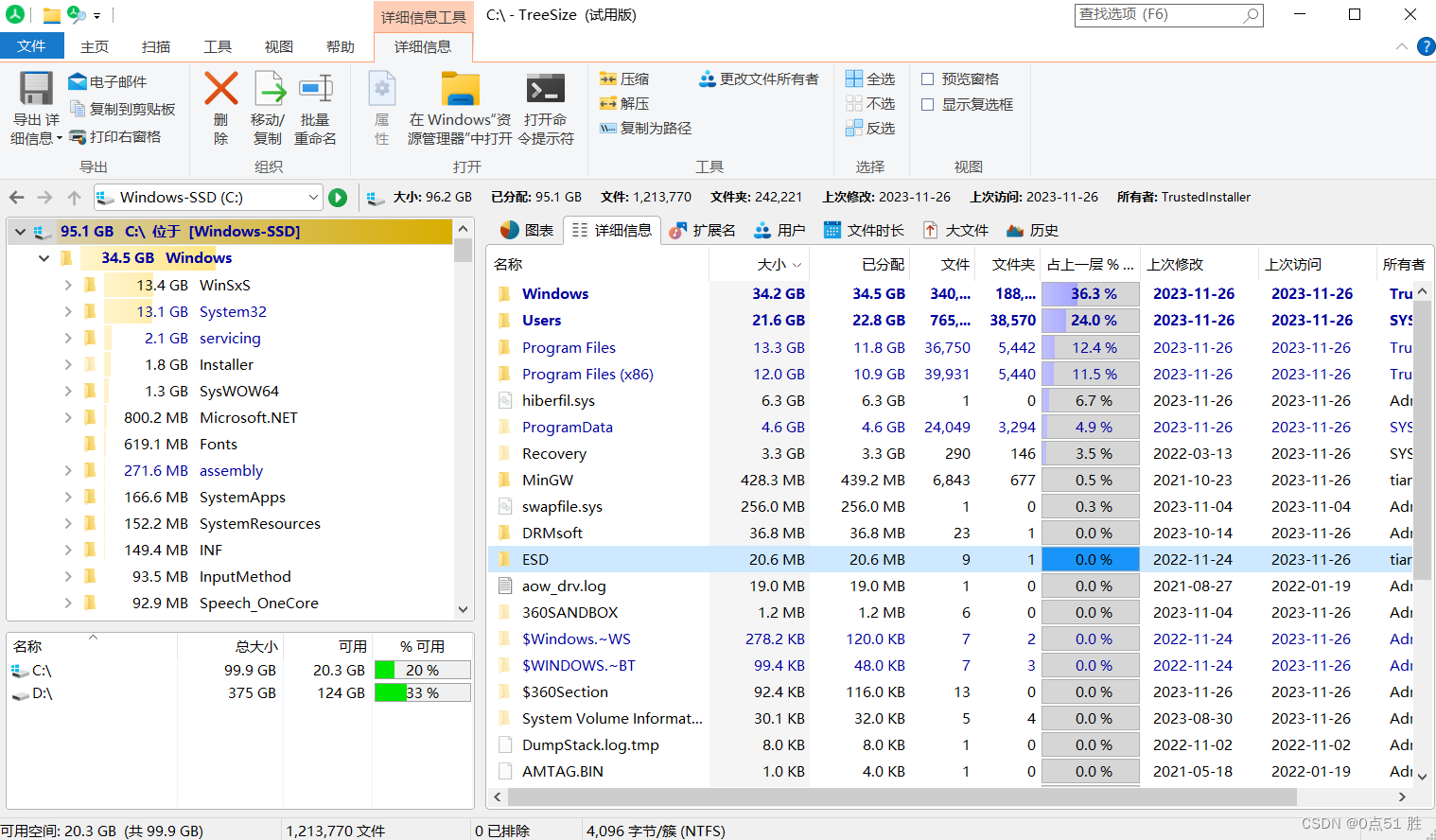
c盘清理——常用方法和工具整理
背景 最近c盘满了,只剩下1-2G,周末有空清理一下。对这块不太熟悉,下面只是把今天网上看到的比较好用的工具整理一下。 使用工具 磁盘大小查看工具——TreeSize(收费) 之前都是右键一个个看每个文件的大小࿰…...
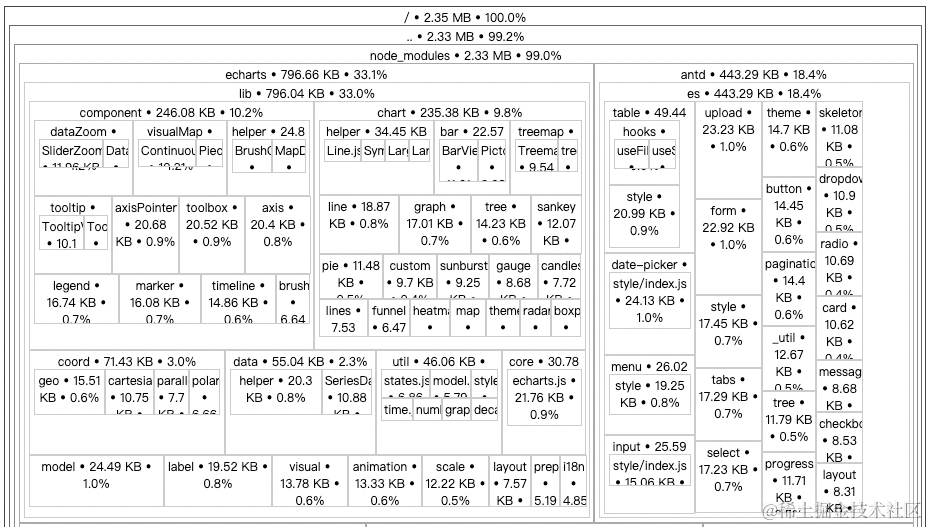
【React】打包体积分析 source-map-explorer
通过分析打包体积,才能知道项目中的哪部分内容体积过大,方便知道哪些包需要进一步优化。 使用步骤 安装分析打包体积的包:npm i source-map-explorer在 package.json 中的 scripts 标签中,添加分析打包体积的命令对项目打包&…...
:在WSL单机搭建Zookeeper伪集群)
Zookeeper(一):在WSL单机搭建Zookeeper伪集群
目录 Zookeeper1 启动单个Zookeeper实例1.1 下载Zookeeper安装包并解压1.2 添加环境变量1.3 修改默认配置1.4 新建数据存储目录和日志目录1.5 启动Zookeeper1.6 停止Zookeeper 2 搭建Zookeeper集群2.1 新建集群目录2.2 配置环境变量2.3 创建节点目录2.4 修改配置2.5 创建节点ID…...

Go语法的特殊之处
上文我们讲了GO模块引入指令Go Mod,本文讲述Go语法的特殊之处 : 单变量 : hello:“hello” Go 语言中新增了一个特殊的运算符:,这个运算符可以使变量在不声明的情况下直接被赋值使用。其使用方法和带值声明变量类似,只是少了var关键字&…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
