向量机SVM原理理解和实战
目录
概念场景导入
点到超平面的距离公式
最大间隔的优化模型
硬间隔、软间隔和非线性 SVM
用 SVM 如何解决多分类问题
1. 一对多法
2. 一对一法
SVM主要原理和特点
原理
优点
缺点
支持向量机模型分类
SVM实战如何进行乳腺癌检测
数据集
字段含义
代码实现
参考文章
概念场景导入
支持向量机主要用于分类和回归任务。由于其在各种数据集上表现出的优异性能,迅速成为流行的机器学习工具之一。
桌子上依然放着红色、蓝色两种球,但是它们的摆放不规律,如下图 所示。如何用一根棍子把这两种颜色分开呢
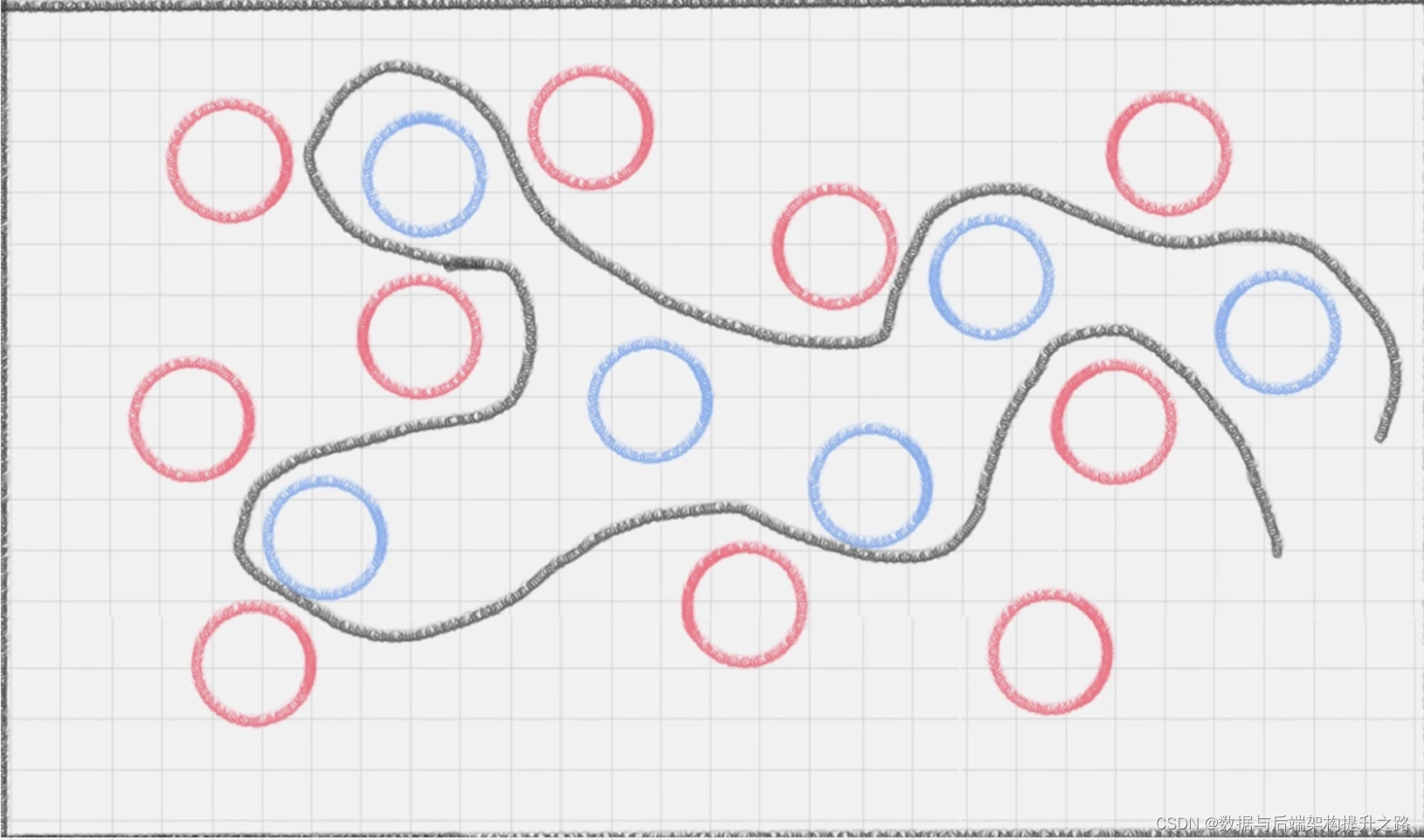
如果在同一个平面上来看,红蓝两种颜色的球是很难分开的。那么 有没有一种方式,可以让它们自然地分开呢?

在这里,二维平面变成了三维空间。原来的曲线变成了一个平面。这个平面,我们就叫做超平 面。

图中的直线 B 更靠近蓝色球,但是在真实环境下,球再多一些的话,蓝色球可能就被 划分到了直线 B 的右侧,被认为是红色球。同样直线 A 更靠近红色球,在真实环境下,如果 红色球再多一些,也可能会被误认为是蓝色球。所以相比于直线 A 和直线 B,直线 C 的划分 更优,因为它的鲁棒性更强。
那怎样才能寻找到直线 C 这个更优的答案呢?这里,我们引入一个 SVM 特有的概念:分类间隔
实际上,我们的分类环境不是在二维平面中的,而是在多维空间中,这样直线 C 就变成了决策面 C。在保证决策面不变,且分类不产生错误的情况下,我们可以移动决策面 C,直到产生两个极限 的位置:如图中的决策面 A 和决策面 B。极限的位置是指,如果越过了这个位置,就会产生 分类错误。这样的话,两个极限位置 A 和 B 之间的分界线 C 就是最优决策面。极限位置到最优决策面 C 之间的距离,就是“分类间隔”,英文叫做 margin。
如果我们转动这个最优决策面,你会发现可能存在多个最优决策面,它们都能把数据集正确分 开,这些最优决策面的分类间隔可能是不同的,而那个拥有“最大间隔”(max margin)的 决策面就是 SVM 要找的最优解。

点到超平面的距离公式
在上面这个例子中,如果我们把红蓝两种颜色的球放到一个三维空间里,你发现决策面就变成 了一个平面。这里我们可以用线性函数来表示,如果在一维空间里就表示一个点,在二维空间 里表示一条直线,在三维空间中代表一个平面,当然空间维数还可以更多,这样我们给这个线 性函数起个名称叫做“超平面”。超平面的数学表达可以写成:
首先,我们定义某类样本集到超平面的距离是这个样本集合内的样本到超平面的最短距离。我 们用 di 代表点 xi 到超平面 wxi+b=0 的欧氏距离。因此我们要求 di 的最小值,用它来代表 这个样本到超平面的最短距离。di 可以用公式计算得出:
这个公式表示点 xi 到由 ωx+b=0 定义的超平面的距离 di,其中 ω 是超平面的法向量,b 是偏置项,分子中的绝对值表示点到超平面的有向距离的绝对值,分母是法向量的范数(也就是长度),用于归一化距离。简而言之,这个公式计算了点到分隔分类的边界的垂直距离。
最大间隔的优化模型
我们的目标就是找出所有分类间隔中最大的那个值对应的超平面。在数学上,这是一个凸优化 问题(凸优化就是关于求凸集中的凸函数最小化的问题,这里不具体展开)。通过凸优化问题,最后可以求出最优的 w 和 b,也就是我们想要找的最优超平面。中间求解的过程会用到 拉格朗日乘子,和 KKT(Karush-Kuhn-Tucker)条件。数学公式比较多,这里不进行展开。
硬间隔、软间隔和非线性 SVM
假如数据是完全的线性可分的,那么学习到的模型可以称为硬间隔支持向量机。换个说法,硬间隔指的就是完全分类准确,不能存在分类错误的情况。软间隔,就是允许一定量的样本分类错误。
我们知道,实际工作中的数据没有那么“干净”,或多或少都会存在一些噪点。所以线性可分 是个理想情况。这时,我们需要使用到软间隔 SVM(近似线性可分),比如下面这种情况:

另外还存在一种情况,就是非线性支持向量机。
比如下面的样本集就是个非线性的数据。图中的两类数据,分别分布为两个圆圈的形状。那么 这种情况下,不论是多高级的分类器,只要映射函数是线性的,就没法处理,SVM 也处理不了。这时,我们需要引入一个新的概念:核函数。它可以将样本从原始空间映射到一个更高维的特质空间中,使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计 算,只是所有的推导是在新的空间,而不是在原来的空间中进行。

所以在非线性 SVM 中,核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核,或者是这些核函数的组合。这些函数的区 别在于映射方式的不同。通过这些核函数,我们就可以把样本空间投射到新的高维空间中。
当然软间隔和核函数的提出,都是为了方便我们对上面超平面公式中的 w* 和 b* 进行求解, 从而得到最大分类间隔的超平面。
用 SVM 如何解决多分类问题
SVM 本身是一个二值分类器,最初是为二分类问题设计的,也就是回答 Yes 或者是 No。而 实际上我们要解决的问题,可能是多分类的情况,比如对文本进行分类,或者对图像进行识别。
针对这种情况,我们可以将多个二分类器组合起来形成一个多分类器,常见的方法有“一对多 法”和“一对一法”两种。
1. 一对多法
假设我们要把物体分成 A、B、C、D 四种分类,那么我们可以先把其中的一类作为分类 1, 其他类统一归为分类 2。这样我们可以构造 4 种 SVM,分别为以下的情况:
(1)样本 A 作为正集,B,C,D 作为负集;
(2)样本 B 作为正集,A,C,D 作为负集;
(3)样本 C 作为正集,A,B,D 作为负集;
(4)样本 D 作为正集,A,B,C 作为负集。
这种方法,针对 K 个分类,需要训练 K 个分类器,分类速度较快,但训练速度较慢,因为每 个分类器都需要对全部样本进行训练,而且负样本数量远大于正样本数量,会造成样本不对称 的情况,而且当增加新的分类,比如第 K+1 类时,需要重新对分类器进行构造。
2. 一对一法
一对一法的初衷是想在训练的时候更加灵活。我们可以在任意两类样本之间构造一个 SVM, 这样针对 K 类的样本,就会有 C(k,2) 类分类器。
比如我们想要划分 A、B、C 三个类,可以构造 3 个分类器:
(1)分类器 1:A、B;
(2)分类器 2:A、C;
(3)分类器 3:B、C。
当对一个未知样本进行分类时,每一个分类器都会有一个分类结果,即为 1 票,最终得票最多 的类别就是整个未知样本的类别。
这样做的好处是,如果新增一类,不需要重新训练所有的 SVM,只需要训练和新增这一类样 本的分类器。而且这种方式在训练单个 SVM 模型的时候,训练速度快。
但这种方法的不足在于,分类器的个数与 K 的平方成正比,所以当 K 较大时,训练和测试的 时间会比较慢。
SVM主要原理和特点
原理
-
最大化边际:SVM的核心理念是寻找一个决策边界(在二维空间中是一条线,在更高维空间中是一个平面或超平面),这个边界能够最大程度地区分不同类别的数据点。SVM尝试最大化各类数据点到决策边界的最小距离,这个距离被称为“边际”。
-
支持向量:决策边界的确切位置由距离它最近的几个训练样本确定,这些样本被称为“支持向量”。SVM模型特别关注这些关键样本。
-
核技巧:对于非线性可分的数据,SVM使用所谓的“核技巧”将数据映射到更高维的空间,从而使得数据在新空间中线性可分。常见的核函数包括线性核、多项式核、径向基函数(RBF)核等。
优点
-
有效性:在中小规模数据集上,尤其是在高维空间中,SVM通常能提供良好的性能。
-
泛化能力强:通过合适的正则化,SVM能够很好地避免过拟合,具有较好的泛化能力。
-
适用性广泛:通过选择合适的核函数,SVM可以用于解决各种类型的数据。
缺点
-
规模限制:对于大规模数据集,SVM的训练时间可能会非常长。
-
核选择和参数调整:核函数的选择和参数的调整需要专业知识,且对模型性能影响很大。
-
解释性:与某些模型相比,SVM模型的解释性较差,尤其是在使用复杂核函数时。
另外,SVM有几种不同的分支模型,主要根据不同的应用场景和数据特性来划分。
支持向量机模型分类
其他分支可看这里~
-
线性SVM:这是最基础的SVM形式,用于处理线性可分的数据集。它寻找一个超平面来最大化两个类别之间的边界。
-
非线性SVM:当数据集不是线性可分的时,非线性SVM使用核技巧来映射数据到一个更高维的空间,以便找到一个能有效分隔数据的超平面。常见的核函数包括多项式核、径向基函数(RBF)核、和Sigmoid核。
-
支持向量回归(SVR):SVR是SVM的一种变体,用于解决回归问题。它尝试找到一个函数,这个函数在给定的误差范围内尽可能地接近训练集中的所有数据点。
-
排序算法经典模型RankSVM:RankSVM的目标是学习一个模型来预测出一种数据点的排列顺序,这种顺序通常是由一些标注的偏好或顺序决定的。比如,在信息检索中,一个查询的结果需要被排序,以便最相关的信息排在最前面。RankSVM试图通过学习数据点之间的相对顺序来实现这一点。RankSVM在搜索引擎的结果排序、推荐系统等领域有广泛的应用。
SVM实战如何进行乳腺癌检测
数据集
GitHub - cystanford/breast_cancer_data: 乳腺癌检测分类数据
字段含义

上面的表格中,mean 代表平均值,se 代表标准差,worst 代表最大值(3 个最大值的平均 值)。每张图像都计算了相应的特征,得出了这 30 个特征值(不包括 ID 字段和分类标识结果字段 diagnosis),实际上是 10 个特征值(radius、texture、perimeter、area、 smoothness、compactness、concavity、concave points、symmetry 和 fractal_dimension_mean)的 3 个维度,平均、标准差和最大值。这些特征值都保留了 4 位 数字。字段中没有缺失的值。在 569 个患者中,一共有 357 个是良性,212 个是恶性。
代码实现
# 加载数据集,你需要把数据放到目录中
data = pd.read_csv("./data.csv")
# 数据探索
# 因为数据集中列比较多,我们需要把dataframe中的列全部显示出来
pd.set_option('display.max_columns', None)
print(data.columns)
print(data.head(5))
print(data.describe())# 将特征字段分成3组
features_mean= list(data.columns[2:12])
features_se= list(data.columns[12:22])
features_worst=list(data.columns[22:32])
# 数据清洗
# ID列没有用,删除该列
data.drop("id",axis=1,inplace=True)
# 将B良性替换为0,M恶性替换为1
data['diagnosis']=data['diagnosis'].map({'M':1,'B':0})# 将肿瘤诊断结果可视化
sns.countplot(data['diagnosis'],label="Count")
plt.show()
# 用热力图呈现features_mean字段之间的相关性
corr = data[features_mean].corr()
plt.figure(figsize=(14,14))
# annot=True显示每个方格的数据
sns.heatmap(corr, annot=True)
plt.show()
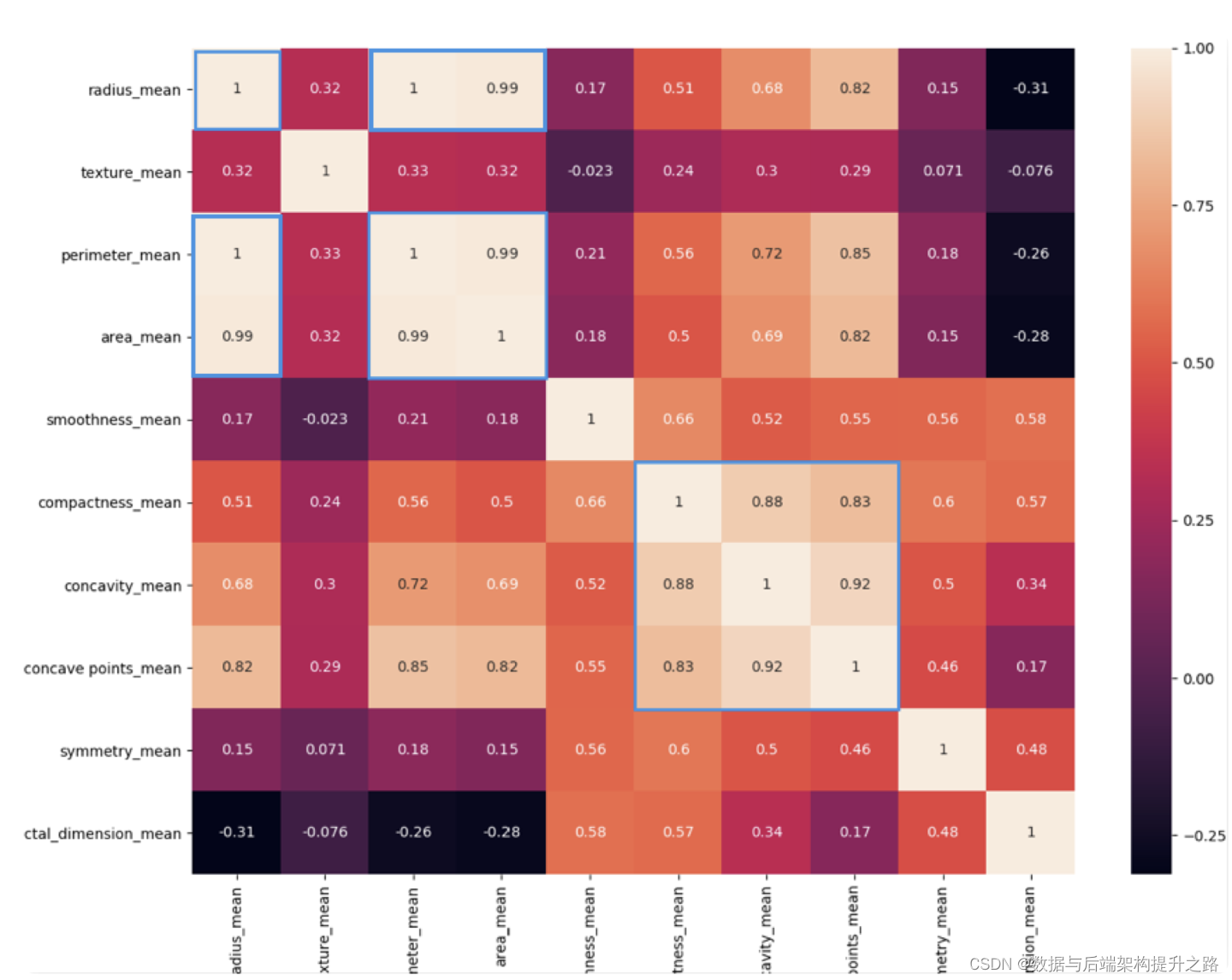
热力图中对角线上的为单变量自身的相关系数是 1。颜色越浅代表相关性越大。所以你能看出 来 radius_mean、perimeter_mean 和 area_mean 相关性非常大,compactness_mean、 concavity_mean、concave_points_mean 这三个字段也是相关的,因此我们可以取其中的 一个作为代表。
特征选择的目的是降维,用少量的特征代表数据的特性,这样也可以增强分类器的泛化能力, 避免数据过拟合。
我们能看到 mean、se 和 worst 这三组特征是对同一组内容的不同度量方式,我们可以保留 mean 这组特征,在特征选择中忽略掉 se 和 worst。同时我们能看到 mean 这组特征中, radius_mean、perimeter_mean、area_mean 这三个属性相关性大
compactness_mean、daconcavity_mean、concave points_mean 这三个属性相关性大。 我们分别从这 2 类中选择 1 个属性作为代表,比如 radius_mean 和 compactness_mean。 这样我们就可以把原来的 10 个属性缩减为 6 个属性,代码如下:
# 特征选择
features_remain = ['radius_mean','texture_mean', 'smoothness_mean','compactness_mean','symmetry_mean', 'fractal_dimension_mean']# 抽取30%的数据作为测试集,其余作为训练集
train, test = train_test_split(data, test_size = 0.3)# in this our main data is splitted into train and test
# 抽取特征选择的数值作为训练和测试数据
train_X = train[features_remain]
train_y=train['diagnosis']
test_X= test[features_remain]
test_y =test['diagnosis']# 采用Z-Score规范化数据,保证每个特征维度的数据均值为0,方差为1
ss = StandardScaler()
train_X = ss.fit_transform(train_X)
test_X = ss.transform(test_X)# 创建SVM分类器
model = svm.SVC()
# 用训练集做训练
model.fit(train_X,train_y)
# 用测试集做预测
prediction=model.predict(test_X)
print('准确率: ', metrics.accuracy_score(test_y,prediction))运行结果:
准确率: 0.9181286549707602
准确率大于90%,说明训练结果还不错
参考文章
一个超强算法模型,SVM !!
SVM Classifier Tutorial | Kaggle
相关文章:

向量机SVM原理理解和实战
目录 概念场景导入 点到超平面的距离公式 最大间隔的优化模型 硬间隔、软间隔和非线性 SVM 用 SVM 如何解决多分类问题 1. 一对多法 2. 一对一法 SVM主要原理和特点 原理 优点 缺点 支持向量机模型分类 SVM实战如何进行乳腺癌检测 数据集 字段含义 代码实现 参…...

什么是 Node.js?
在 Node.js 出现之前,最常见的 JavaScript 运行时环境是浏览器,也叫做 JavaScript 的宿主环境。浏览器为 JavaScript 提供了 DOM API,能够让 JavaScript 操作浏览器环境(JS 环境)。 2009 年初 Node.js 出现了…...
系列九、声明式事务(xml方式)
一、概述 声明式事务(declarative transaction management)是Spring提供的对程序事务管理的一种方式,Spring的声明式事务顾名思义就是采用声明的方式来处理事务。这里所说的声明,是指在配置文件中声明,用在Spring配置文件中声明式的处理事务来…...
c盘清理——常用方法和工具整理
背景 最近c盘满了,只剩下1-2G,周末有空清理一下。对这块不太熟悉,下面只是把今天网上看到的比较好用的工具整理一下。 使用工具 磁盘大小查看工具——TreeSize(收费) 之前都是右键一个个看每个文件的大小࿰…...
【React】打包体积分析 source-map-explorer
通过分析打包体积,才能知道项目中的哪部分内容体积过大,方便知道哪些包需要进一步优化。 使用步骤 安装分析打包体积的包:npm i source-map-explorer在 package.json 中的 scripts 标签中,添加分析打包体积的命令对项目打包&…...
:在WSL单机搭建Zookeeper伪集群)
Zookeeper(一):在WSL单机搭建Zookeeper伪集群
目录 Zookeeper1 启动单个Zookeeper实例1.1 下载Zookeeper安装包并解压1.2 添加环境变量1.3 修改默认配置1.4 新建数据存储目录和日志目录1.5 启动Zookeeper1.6 停止Zookeeper 2 搭建Zookeeper集群2.1 新建集群目录2.2 配置环境变量2.3 创建节点目录2.4 修改配置2.5 创建节点ID…...

Go语法的特殊之处
上文我们讲了GO模块引入指令Go Mod,本文讲述Go语法的特殊之处 : 单变量 : hello:“hello” Go 语言中新增了一个特殊的运算符:,这个运算符可以使变量在不声明的情况下直接被赋值使用。其使用方法和带值声明变量类似,只是少了var关键字&…...

浏览器v8垃圾回收机制和内存泄漏分析-初级
借鉴:一文搞懂V8引擎的垃圾回收 - 掘金 (juejin.cn) 聊聊V8引擎的垃圾回收 - 掘金 (juejin.cn) 内存泄漏方向: 1、全局变量 未手动清除 2、定时器 未手动清除 3、闭包中使用了匿名函数 未手动清除 4、dom被赋值使用后 未手动清除 其他解决方式 1、…...
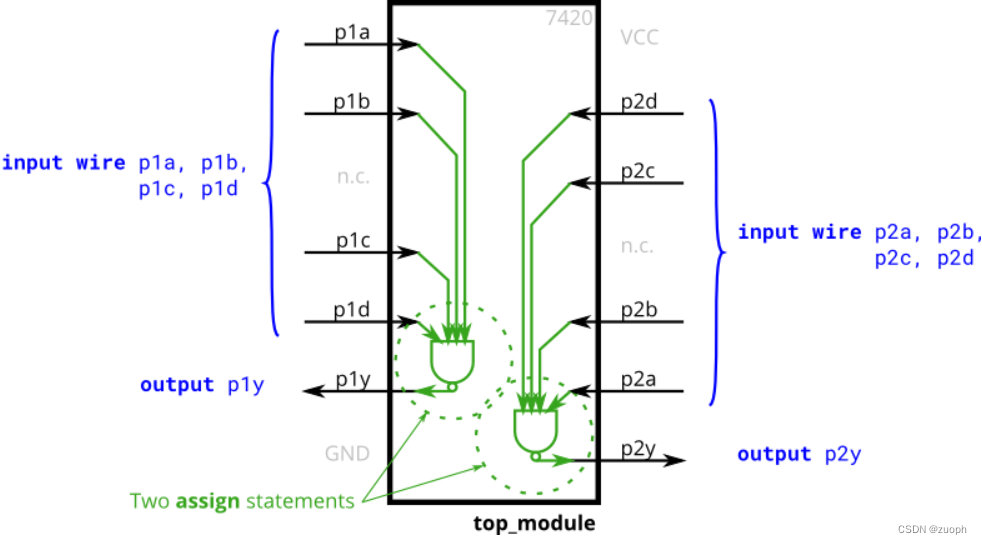
hdlbits系列verilog解答(7420 chip)-49
文章目录 一、问题描述二、verilog源码三、仿真结果一、问题描述 本次将实现7420逻辑芯片,它内部有2个4输入的与非门电路,外部有8个输入和2个输出管脚,功能框图如下所示: 二、verilog源码 module top_module ( input p1a, p1b, p1c, p1d,output p1y,input p2a, p2b, p2c…...

Sentinel核心类解读:Entry
默认情况下,Sentinel会将controller中的方法作为被保护资源,Sentinel中的资源用Entry来表示。 Sentinel中Entry可以理解为每次进入资源的一个凭证,如果调用SphO.entry()或者SphU.entry()能获取Entry对象,代表获取了凭证ÿ…...

YOLOv8改进 | SAConv可切换空洞卷积(附修改后的C2f+Bottleneck)
论文地址:官方论文地址 代码地址:官方代码地址 一、本文介绍 本文给大家带来的改进机制是可切换的空洞卷积(Switchable Atrous Convolution, SAC)是一种创新的卷积网络机制,专为增强物体检测和分割任务中的特征提取而…...
可以ping通IP但是无法远程连接-‘telnet‘ 不是内部或外部命令,也不是可运行的程序或批处理文件
起因 一开始远程连接IP,报错,怀疑是自己网络原因,但是同事依旧无法连接 怀疑是自己防火墙的原因,查看关闭依旧无法连接 问题 两个地址可以ping通排除防火墙缘故 怀疑端口,测试端口 然 解决方案 winR 输入control…...
使用VC++设计程序:实现常见的三种图像插值算法:最近邻插值,双线性插值,立方卷积插值
图像放大的三种插值算法 获取源工程可访问gitee可在此工程的基础上进行学习。 该工程的其他文章: 01- 一元熵值、二维熵值 02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转 03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器 04-…...

多级嵌套vue同步调用用法
//需求 要求同步调用initGame2方法 //调用方法 this.initSocket(); //定义方法为同步 async initSocket() { //调用为同步 await this.initGame2(); //定义方法为同步 async initGame2() {const e await w({ url: //定义w方法 const w e.create({ baseURL: http://my_url:8…...
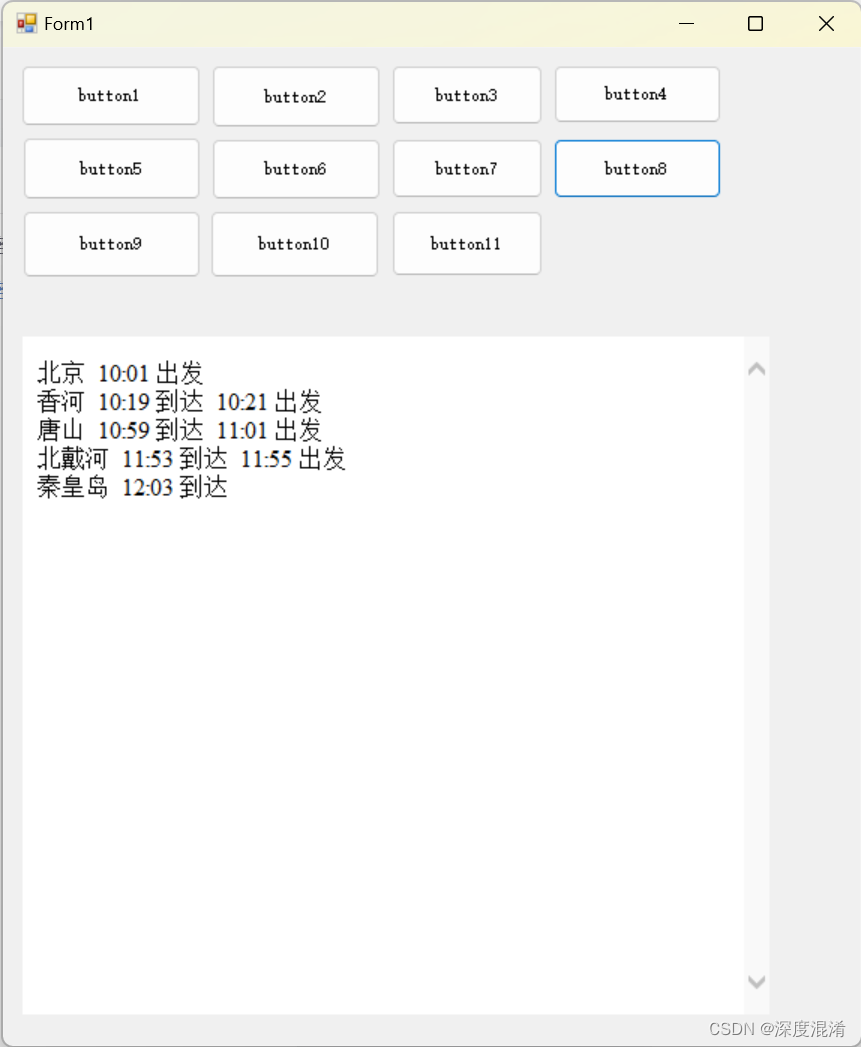
C#,《小白学程序》第八课:列表(List)其二,编制《高铁列车时刻表》与时间DateTime
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary&g…...

高德地图使用逆地理编码服务
进入高德地图开发者平台申请web服务,并获取web服务生成的key下面是高德地图官网的逆地理编码服务使用说明https://lbs.amap.com/api/webservice/guide/api/georegeo/ getAddressByLocation(latitude, longitude) {const key key; // 高德地图key密钥const url h…...

ArgoCD基本组件
ArgoCD有5个基本组件, $ kubectl get po -n argocd NAME READY STATUS RESTARTS AGE argocd-application-controller-0 1/1 Running 0 19h argocd-dex-server-767fb49f59-7rxn7 1/1 Running 0…...
技术分享 | 在 IDE 插件开发中接入 JCEF 框架
项目背景 当前的开发环境存在多种不同语言的 IDE,如 JetBrains 全家桶、Eclipse、Android Studio 和 VS Code 等等。由于每个 IDE 各有其特定的语言和平台要求,因此开发 IDE 插件时,需要投入大量资源才能尽可能覆盖大部分工具。同时…...
ubuntu 使用webrtc_ros 编译linux webrtc库
ubuntu 使用webrtc_ros 编译linux webrtc库 webrtc_ros 使用WebRTC流式传输ROS图像主题 该节点提供了一个WebRTC对等方,可以将其配置为流ROS图像主题并接收发布到ROS图像主题的流。 该节点托管一个提供简单测试页面的Web服务器,并提供可用于创建和配置W…...
网络通信基础概念介绍
网络通信基础概念介绍 局域网LAN 局域网,即 Local Area Network,简称LAN。 局域网内的主机之间能方便的进行网络通信,又称为内网;局域网和局域网之间在没有连接的情况下,是无法通信的。 局域网是指在一个相对较小的…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...

