读书笔记：《宽客人生：依曼纽尔·德曼》
金融工程，也叫数量金融，洞察了证券价值与不确定性之间的关系。
布莱克-斯科尔斯模型可以告诉我们如何利用标的股票来复制期权，以及复制期权的成本，做市商利用此来复制期权，以规避无法从其他人那里购买合适价格的期权的风险。
BS模型可以使得做市商现在可以在不承担市场风险的前提下利用标的股票来制作，出售客户愿意承担的风险。
可以通过股票和现金的组合来模拟期权的价格变化，不断调整股票和现金的配比，最终获得与股票期权正好相等的收益。
做市商不仅可以制作期权，还可以分解期权为股票，并收取制作费用，以承担模型不准确的风险。
在物理学界，总有人可以完全超出你的想象，可以意识到即使你能够理解经典物理论文的理论框架，但你永远不可能自己创造出这样的理论。
改进带来笔直的道路，但没有改进的弯曲道路才是天才之路。
你能做你想做的，但你不能要你想要的。你只能控制过程，而不能控制结果。
股票的未来价格变化不确定，但是债券的未来价格变化会最终回归到票面价值。
布莱克-德曼-托伊为模型，《利率单因子模型及其在国债期权上的应用》
期权的报价是对未来短期波动率的预期，债券的报价是对未来短期利率的预期。
相关文章：
读书笔记：《宽客人生：依曼纽尔·德曼》
金融工程，也叫数量金融，洞察了证券价值与不确定性之间的关系。 布莱克-斯科尔斯模型可以告诉我们如何利用标的股票来复制期权，以及复制期权的成本，做市商利用此来复制期权，以规避无法从其他人那里购买合适价格的期权的…...
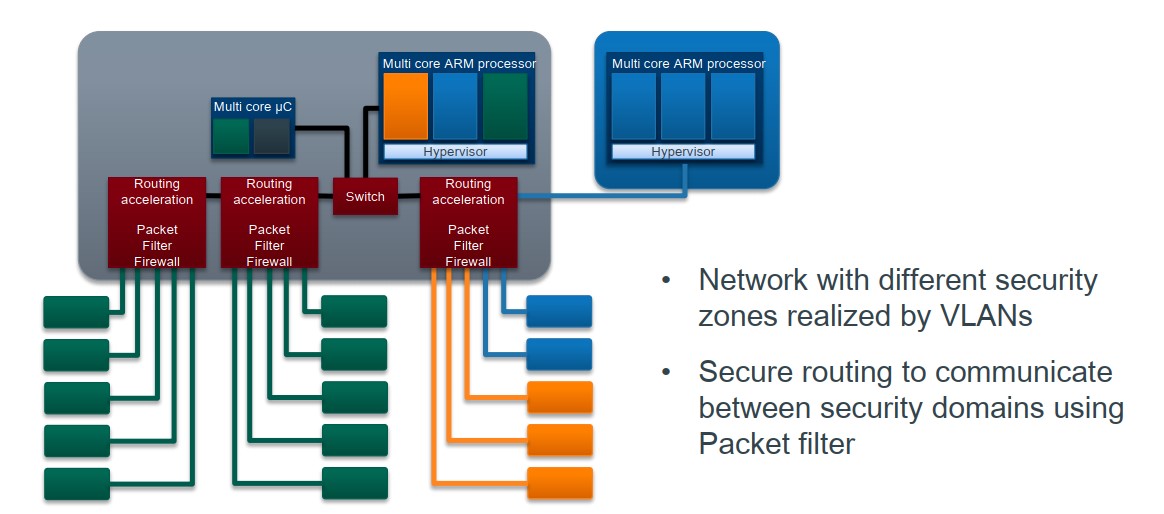
车载通信架构 —— 传统车内通信网络LIN总线（低成本覆盖低速场景）
车载通信架构 —— 传统车内通信网络LIN总线（低成本覆盖低速场景） 我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 屏蔽力是信息过载时代一个人的特殊竞争力，任何消耗你的人和事，多看一眼都是…...
单例模式与多线程
目录 前言 正文 1.立即加载/饿汉模式 2.延迟加载/懒汉模式 1.延迟加载/懒汉模式解析 2.延迟加载/懒汉模式的缺点 3.延迟加载/懒汉模式的解决方案 （1）声明 synchronized 关键字 （2）尝试同步代码块 （3&am…...
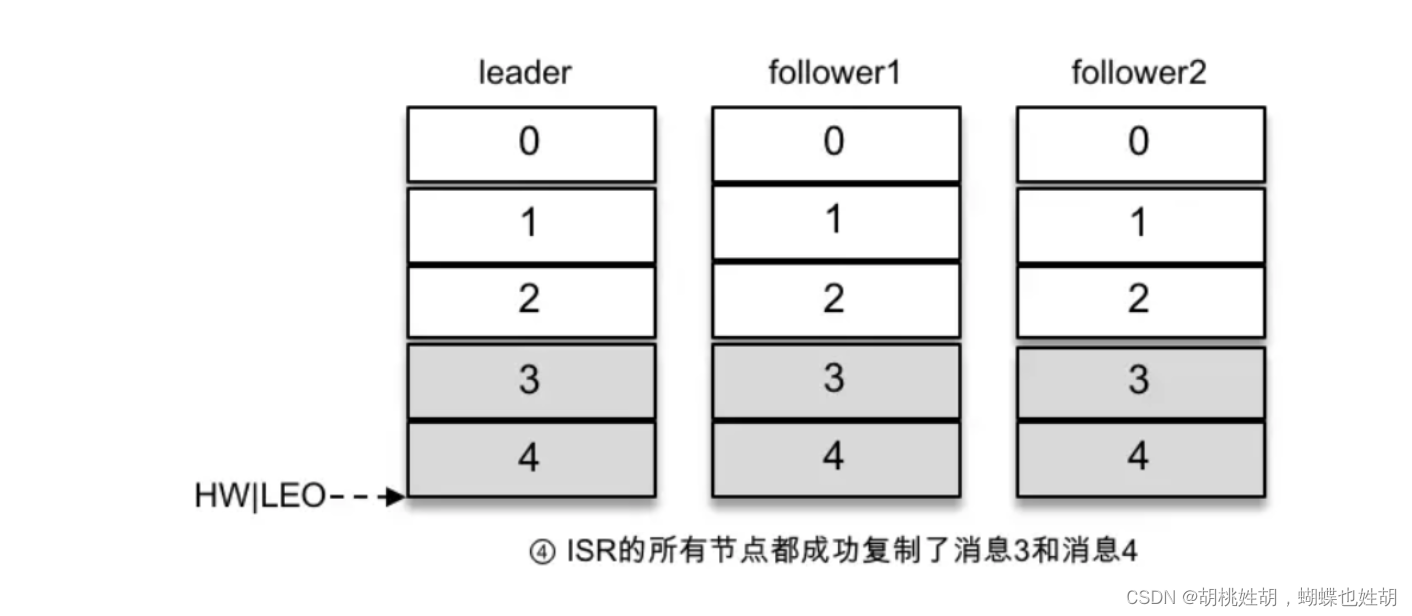
Kafka系列 - Kafka一篇入门
Kafka是一个分布式流式处理平台。很多分布式处理系统，例如Spark，Flink等都支持与Kafka集成。 Kafka使用场景 消息系统：Kafka实现了消息顺序性保证和回溯消费。存储系统：Kafka把消息持久化到磁盘，相比于其他基于内存的…...
百度 文心一言 sdk 试用
JMaven Central: com.baidu.aip:java-sdk (sonatype.com) Java sdk地址如上： 文心一言开发者 文心一言 (baidu.com) ERNIE Bot SDK https://yiyan.baidu.com/developer/doc#Fllzznonw ERNIE Bot SDK提供便捷易用的接口，可以调用文心一言的能力&#…...
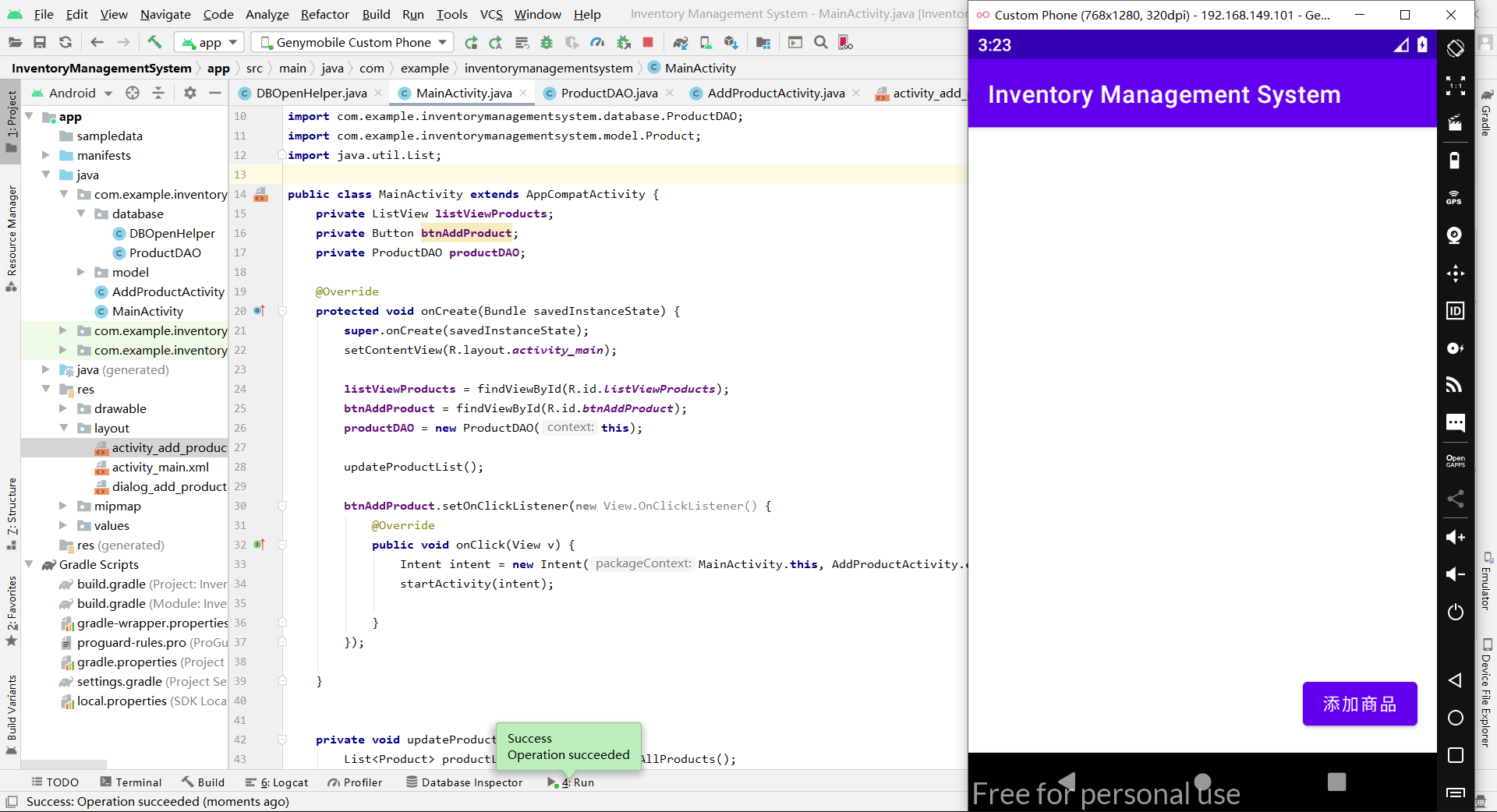
SQLite 和 SQLiteDatabase 的使用
实验七：SQLite 和 SQLiteDatabase 的使用 7.1 实验目的 本次实验的目的是让大家熟悉 Android 中对数据库进行操作的相关的接口、类等。SQLiteDatabase 这个是在 android 中数据库操作使用最频繁的一个类。通过它可以实现数据库的创建或打开、创建表、插入数据、删…...
Dempster-Shafer（D-S）证据理论的基本定义和详细分析，优点，缺点，应用！！（系列1）
文章目录 前言一、D-S证据理论的应用：二、D-S证据理论的优点：三、D-S证据理论的缺陷：四、D-S组合规则：总结 前言 Dempster-Shafer（D-S）证据理论是一种不精确推理理论，也称为Dempster/Shafer证据…...
Leetcode—15.三数之和【中等】
2023每日刷题（四十一） Leetcode—15.三数之和 实现代码 class Solution { public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ans;int i, j, k;int s,…...
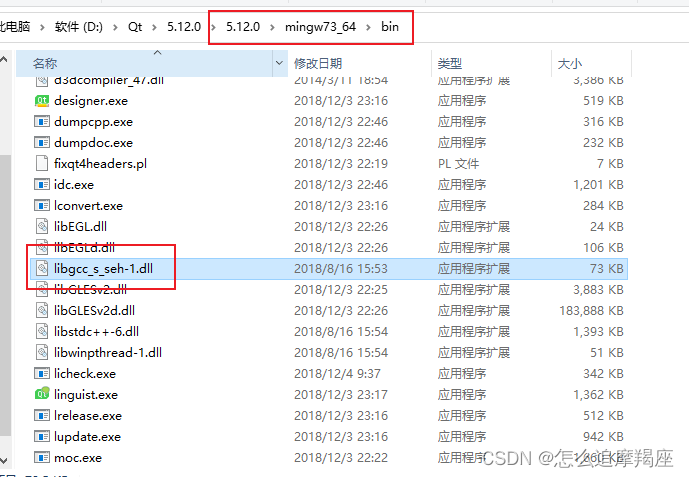
3、Qt使用windeploy工具打包可执行文件
新建一个文件夹，把要打包的可执行文件exe拷贝过来 点击输入框，复制一下文件夹路径 点击电脑左下角，找到Qt文件夹， 点击打开 “Qt 5.12.0 for Desktop” （我安装的是Qt 5.12.0版本） 输入“cd bin”ÿ…...
[DFS深度优先搜索]集合里的乘法
集合里的乘法 题目描述 给定一个目标数T和一个整数集合S，判断是否存在S的一个非空子集，子集中的数相乘的积为T。 关于输入 输入为两行。 第一行为目标数T，和S中的元素个数N，以空格隔开。 第二行为S中的N个元素，以空…...
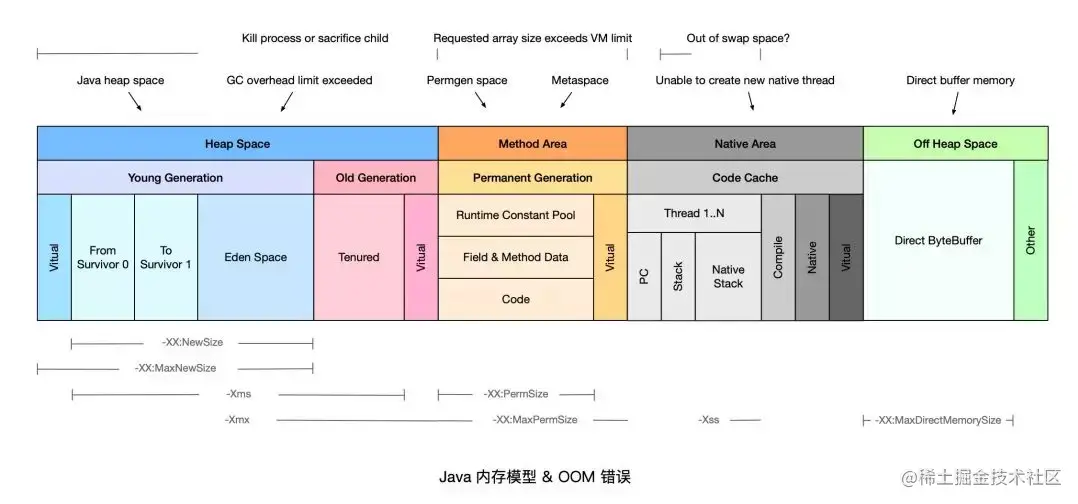
K8s 中 Pod OOMKilled 原因
目录 Exit Code 137 解决方案 JVM 感知 cgroup 限制 使用 JDK9 的容器感知机制尝试 问题分析 容器内部感知 CGroup 资源限制 在 Java10 中，改进了容器集成 JVM 参数 MaxDirectMemorySize -XX:MaxDirectMemorySize 的默认值是什么？ 其他获取 ma…...
为什么程序员最应该学习的是运营与销售，而不是技术？
大概几个月前，我加入了某副业交流群。这里人才很多，不光是传统意义上的程序员，也有公司老板、偏门大佬、产品经理等。 群里的聊天主题就是搞钱俩字，大家讨论着如何搞钱，分享每日收益情况，以及自己做的产品等…...
MySql数据库常用指令（五）多表连接
MySql数据库常用指令（五）多表连接 一、内连接,或等值连接二、左连接三、右连接 实际应用中，我们常常要连接几个不同的MySQL表，因此在 SELECT, UPDATE 和 DELETE 语句中使用 Mysql 的 JOIN 来联合多表查询 INNER JOIN（内…...
Centos7使用rpm安装mysql 5.7.43
Centos7使用rpm安装mysql 5.7.43 1、下载rpm包 wget https://downloads.mysql.com/archives/get/p/23/file/mysql-5.7.43-1.el7.x86_64.rpm-bundle.tar2、解压并安装 tar xf mysql-5.7.43-1.el7.x86_64.rpm-bundle.tar yum -y install mysql-*3、按需修改mysql配置 #注意&a…...
补充：如何提高selenium的运行速度？
已经通读该专栏文章的同学，或许对UI自动化测试有了一定的掌握，细心的同学肯定会发现一个问题，当用例量达到一定程度时，对于整体用例的执行速度肯定不会很满意。除了应用多线程运行用例的方式加快速度，有没有其他的方法呢？ 今天告诉大家，方法是有的！也是本人新学的。即…...
使用Python+Redis实现文章投票网站后端功能
1．实现投票功能，2．创建文章数据，3．对文章进行排序。 实现投票功能 实现投票功能，要注重文章的时效性与投票的公平性，所以需要给投票功能加上一些约束条件： 文章发布满一个星期后&…...
SpringBoot 环境使用 Redis + AOP + 自定义注解实现接口幂等性
目录 一、前言二、主流实现方案介绍2.1、前端按钮做加载状态限制（必备）2.2、客户端使用唯一标识符2.3、服务端通过检测请求参数进行幂等校验（本文使用） 三、代码实现3.1、POM3.2、application.yml3.3、Redis配置类3.4、自定义注解…...
Leetcode—18.四数之和【中等】
2023每日刷题（四十一） Leetcode—18.四数之和 实现代码 class Solution { public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ans;sort(nums.begin(), nums.end());int n …...
springsecurity6配置二
一、springsecurity6自定义认证异常处理器 1.1 AuthenticationEntryPointImpl.java package com.school.information.core.security.handler;import com.alibaba.fastjson.JSON; import com.school.information.enums.result.ResultStatusEnum; import com.school.informatio…...
)
php如何对比浮点数大小(bccomp函数)
第一部分，常规例子： 例1：左边比右边小，结果：-1 //示例，左边比右边小返回值：-1 $price1 2.14; $price2 3.14; $result bccomp($price1, $price2, 2); echo 对比结果：.$result;//…...
MPNet：旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
使用分级同态加密防御梯度泄漏
抽象 联邦学习 （FL） 支持跨分布式客户端进行协作模型训练，而无需共享原始数据，这使其成为在互联和自动驾驶汽车 （CAV） 等领域保护隐私的机器学习的一种很有前途的方法。然而，最近的研究表明&…...
CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架，相比 MapReduce 具有以下核心优势： 内存计算：数据可常驻内存，迭代计算性能提升 10-100 倍（文档段落：3-79…...
2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡（如 HAProxy、AWS NLB、阿里 SLB）发起上游连接时，将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后，ngx_stream_realip_module 从中提取原始信息…...
【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多，如何一步解决，采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集（每个目录代表一个类别，目录下是该类别的所有图片），你需要进行以下配置步骤&#x…...
12.找到字符串中所有字母异位词
🧠 题目解析 题目描述： 给定两个字符串 s 和 p，找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义： 若两个字符串包含的字符种类和出现次数完全相同，顺序无所谓，则互为…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流：用一个简单脚本，秒杀视频片头广告，还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农，平时写代码之余看看电影、补补片，是再正常不过的事。 电影嘛，要沉浸，…...
机器学习的数学基础：线性模型
线性模型 线性模型的基本形式为： f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法，得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...