TDlib readme
不同开发语言使用TDlib的连接入口:td/example/README.md at master · tdlib/td (github.com)
如golang:td/example/README.md at master · tdlib/td (github.com)
相关文章:

TDlib readme
不同开发语言使用TDlib的连接入口:td/example/README.md at master tdlib/td (github.com) 如golang:td/example/README.md at master tdlib/td (github.com)...

紧急救援【Dijkstra】
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的…...

「Verilog学习笔记」数据累加输出
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 在data_out准备好,valid_b拉高时,如果下游的ready_b为低,表示下游此时不能接收本模块的数据,那么,将会拉低ready…...
typeof,instanceof
1.typeof typeof运算符返回的结果是以小写的字符串表示的变量的类型 2.instanceof instanceof运算符用于判断右边构造函数的原型对象是否在左边对象的原型链上 let arr[]let obj{}let datenew Dateconsole.log(arr instanceof Array)console.log(arr instanceof Object)conso…...

传统数仓和clickhouse对比
背景 传统数仓一般都是HiveSparkSql作为代表,不过也包括Kylin等,而clickhouse是实时OLAP的代表,我们简单看下他们的对比 传统数仓和clickhouse对比 HiveSparkSQL的传统数仓: 1.数据更新速度慢,由于传统数仓一般都是…...
burpsuite的大名早有耳闻,近日得见尊荣,倍感荣幸
问题: burpsuite中文乱码何解? burpsuite 与君初相识,犹如故人归。 burpsuite早有耳闻,近日得见真容,果然非同凡响。 Burp Suite is a comprehensive suite of tools for web application security testing. burp …...
Xshell连接VMware虚拟机中的CentOS
Xshell连接VMware虚拟机中的CentOShttps://www.cnblogs.com/niuben/p/13157291.html 步骤: 1. 检查Linux虚拟机的网络连接模式,确保它是NAT模式。(由于只在本机进行连接,所以没有选择桥接模式。当然,桥接模式的配置会…...
JVM类加载的过程和JVM垃圾回收机制
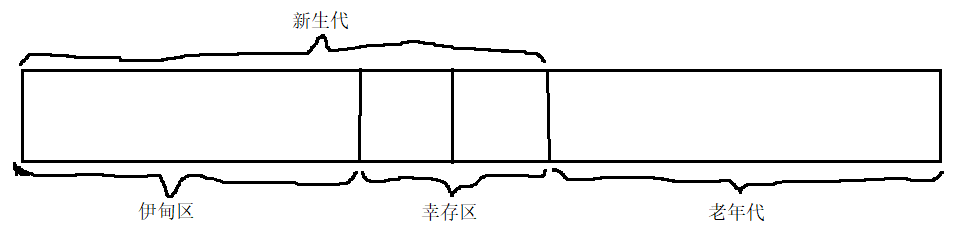
文章目录 一、JVM类加载的过程1.1类加载的基本流程1.1.1加载1.1.2验证1.1.3准备1.1.4解析1.1.5初始化 1.2双亲委派模型 二、JVM垃圾回收机制2.1找到垃圾2.1.1引用计数(比如Python,PHP中用到)2.1.2可达性分析(比如Java中用到) 2.2释放垃圾2.2.1标记清除2.2.2复制算法…...

【git error|SourceTree】error: bad signature 0x00000000 fatal: index file corrupt
报错 error: bad signature 0x00000000 fatal: index file corrupt 场景 在使用git add . 提交代码到缓冲区时或使用SourceTree时电脑宕机,重启后再次提交代码会出现该提示 原因分析 .git目录下的index文件损坏 解决方式 //删除索引文件 rm -f .git/index //回…...

读书笔记:《宽客人生:依曼纽尔·德曼》
金融工程,也叫数量金融,洞察了证券价值与不确定性之间的关系。 布莱克-斯科尔斯模型可以告诉我们如何利用标的股票来复制期权,以及复制期权的成本,做市商利用此来复制期权,以规避无法从其他人那里购买合适价格的期权的…...
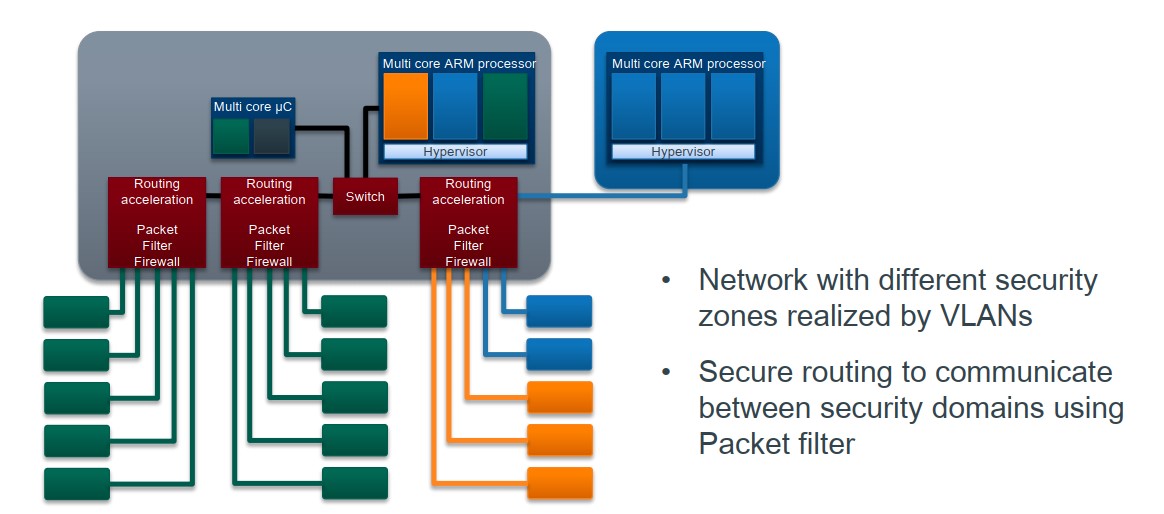
车载通信架构 —— 传统车内通信网络LIN总线(低成本覆盖低速场景)
车载通信架构 —— 传统车内通信网络LIN总线(低成本覆盖低速场景) 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是…...

单例模式与多线程
目录 前言 正文 1.立即加载/饿汉模式 2.延迟加载/懒汉模式 1.延迟加载/懒汉模式解析 2.延迟加载/懒汉模式的缺点 3.延迟加载/懒汉模式的解决方案 (1)声明 synchronized 关键字 (2)尝试同步代码块 (3&am…...
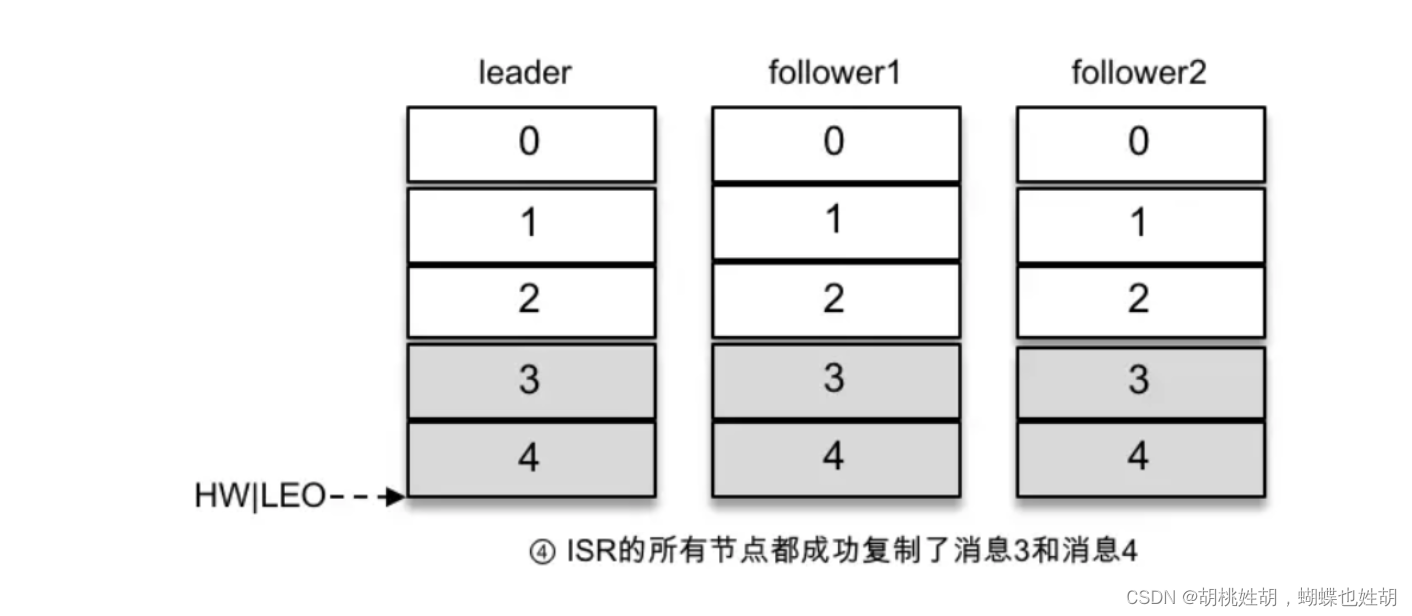
Kafka系列 - Kafka一篇入门
Kafka是一个分布式流式处理平台。很多分布式处理系统,例如Spark,Flink等都支持与Kafka集成。 Kafka使用场景 消息系统:Kafka实现了消息顺序性保证和回溯消费。存储系统:Kafka把消息持久化到磁盘,相比于其他基于内存的…...

百度 文心一言 sdk 试用
JMaven Central: com.baidu.aip:java-sdk (sonatype.com) Java sdk地址如上: 文心一言开发者 文心一言 (baidu.com) ERNIE Bot SDK https://yiyan.baidu.com/developer/doc#Fllzznonw ERNIE Bot SDK提供便捷易用的接口,可以调用文心一言的能力&#…...
SQLite 和 SQLiteDatabase 的使用
实验七:SQLite 和 SQLiteDatabase 的使用 7.1 实验目的 本次实验的目的是让大家熟悉 Android 中对数据库进行操作的相关的接口、类等。SQLiteDatabase 这个是在 android 中数据库操作使用最频繁的一个类。通过它可以实现数据库的创建或打开、创建表、插入数据、删…...

Dempster-Shafer(D-S)证据理论的基本定义和详细分析,优点,缺点,应用!!(系列1)
文章目录 前言一、D-S证据理论的应用:二、D-S证据理论的优点:三、D-S证据理论的缺陷:四、D-S组合规则:总结 前言 Dempster-Shafer(D-S)证据理论是一种不精确推理理论,也称为Dempster/Shafer证据…...

Leetcode—15.三数之和【中等】
2023每日刷题(四十一) Leetcode—15.三数之和 实现代码 class Solution { public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());vector<vector<int>> ans;int i, j, k;int s,…...
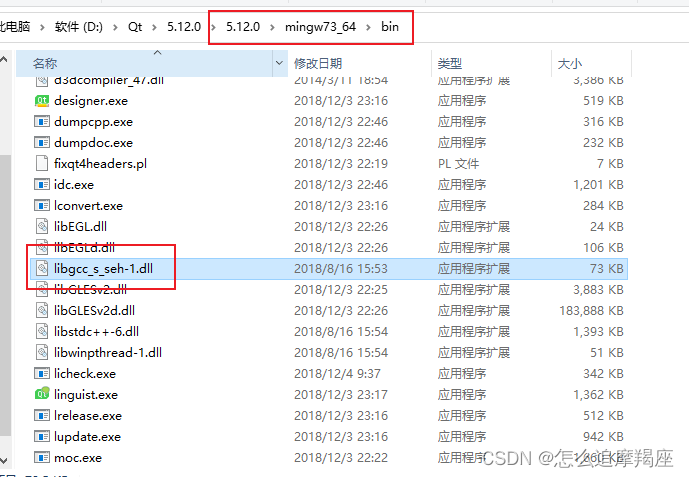
3、Qt使用windeploy工具打包可执行文件
新建一个文件夹,把要打包的可执行文件exe拷贝过来 点击输入框,复制一下文件夹路径 点击电脑左下角,找到Qt文件夹, 点击打开 “Qt 5.12.0 for Desktop” (我安装的是Qt 5.12.0版本) 输入“cd bin”ÿ…...

[DFS深度优先搜索]集合里的乘法
集合里的乘法 题目描述 给定一个目标数T和一个整数集合S,判断是否存在S的一个非空子集,子集中的数相乘的积为T。 关于输入 输入为两行。 第一行为目标数T,和S中的元素个数N,以空格隔开。 第二行为S中的N个元素,以空…...
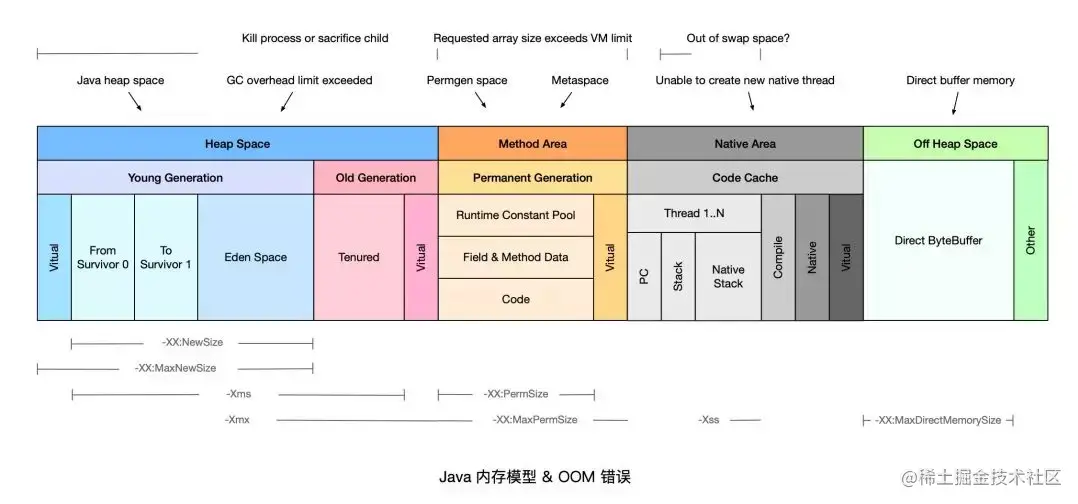
K8s 中 Pod OOMKilled 原因
目录 Exit Code 137 解决方案 JVM 感知 cgroup 限制 使用 JDK9 的容器感知机制尝试 问题分析 容器内部感知 CGroup 资源限制 在 Java10 中,改进了容器集成 JVM 参数 MaxDirectMemorySize -XX:MaxDirectMemorySize 的默认值是什么? 其他获取 ma…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
