阶梯排列硬币
题意:
你总共有 n 枚硬币,并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯,其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。
给你一个数字 n ,计算并返回可形成 完整阶梯行 的总行数。
示例 1:

输入:n = 5
输出:2
解释:因为第三行不完整,所以返回 2 。
示例 2:

输入:n = 8
输出:3
解释:因为第四行不完整,所以返回 3 。
提示:
1 <= n <= 231 - 1
题目来源: https://leetcode.cn/problems/arranging-coins/description/
解题方法:
方法一:迭代递减
//迭代递减
function arrangeCoins($n) {for($i = 1; $i <= $n; $i++){$n -= $i;if($n == 0 || $n < $i+1){return $i;}}
}
方法二:二分法(利用)

// 等差数列{an}的通项公式为:an=a1+(n-1)d。前n项和公式为:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2,d为公差
function arrangeCoins($n) {if($n == 1 || $n == 2){return 1;}$start = 1;$end = $n;while($start < $end){$mid = $start + intval(($end - $start + 1) / 2);$sum = ($mid * ($mid + 1)) / 2; //Sn=n(a1+an)/2 => n=$mid, a1=1, an=$midif($sum > $n){$end = $mid - 1;}else{$start = $mid;}}return $start;
}
方法三:数学,一元二次方程求根


// 数学,一元二次方程求根
function arrangeCoins($n) {return intval((pow(8 * $n + 1, 0.5) - 1) / 2);
}
参考:
作者:力扣官方题解
链接:https://leetcode.cn/problems/arranging-coins/solutions/1038396/pai-lie-ying-bi-by-leetcode-solution-w52c/
来源:力扣(LeetCode)
相关文章:

阶梯排列硬币
题意: 你总共有 n 枚硬币,并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯,其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。 给你一个数字 n ,计算并返回可形成 完整阶梯行 的总行数。 示例 1ÿ…...

HarmonyOS应用开发者高级认证【题库答案】
HarmonyOS应用开发者基础认证【题库答案】 一、判断题 云函数打包完成后,需要到AppGallery Connect创建对应函数的触发器才可以在端侧中调用(错)在column和Row容器组件中,aligntems用于设置子组件在主轴方向上的对齐格式…...

【解答】关于Linux内核的一些疑问
GNU计划是什么 GNU计划是由理查德斯托曼在1983年9月27日公开发起的自由软件集体协作计划,其目标是创建一套完全自由的操作系统GNU。这个操作系统的内容软件完全以GPL方式发布,意味着用户拥有运行、复制、分发、学习、修改和改进该软件的自由。 GNU的命名…...
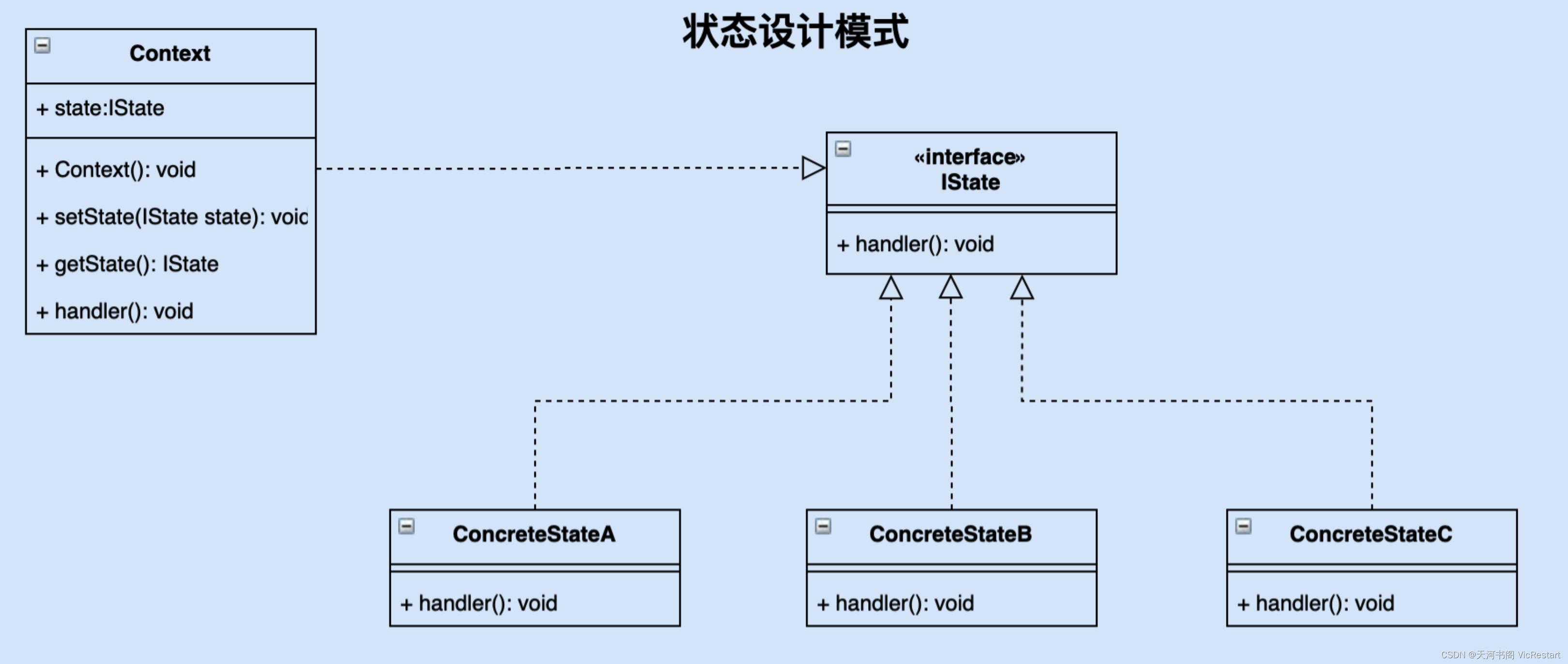
状态设计模式是什么?什么是 State 状态设计模式?Python 状态设计模式示例代码
什么是 State 状态设计模式? 状态设计模式是一种行为型设计模式,它允许一个对象在其内部状态发生改变时改变其行为,使其看起来好像改变了其类。状态模式主要解决的问题是:当一个对象的行为取决于它的状态,并且在运行时…...
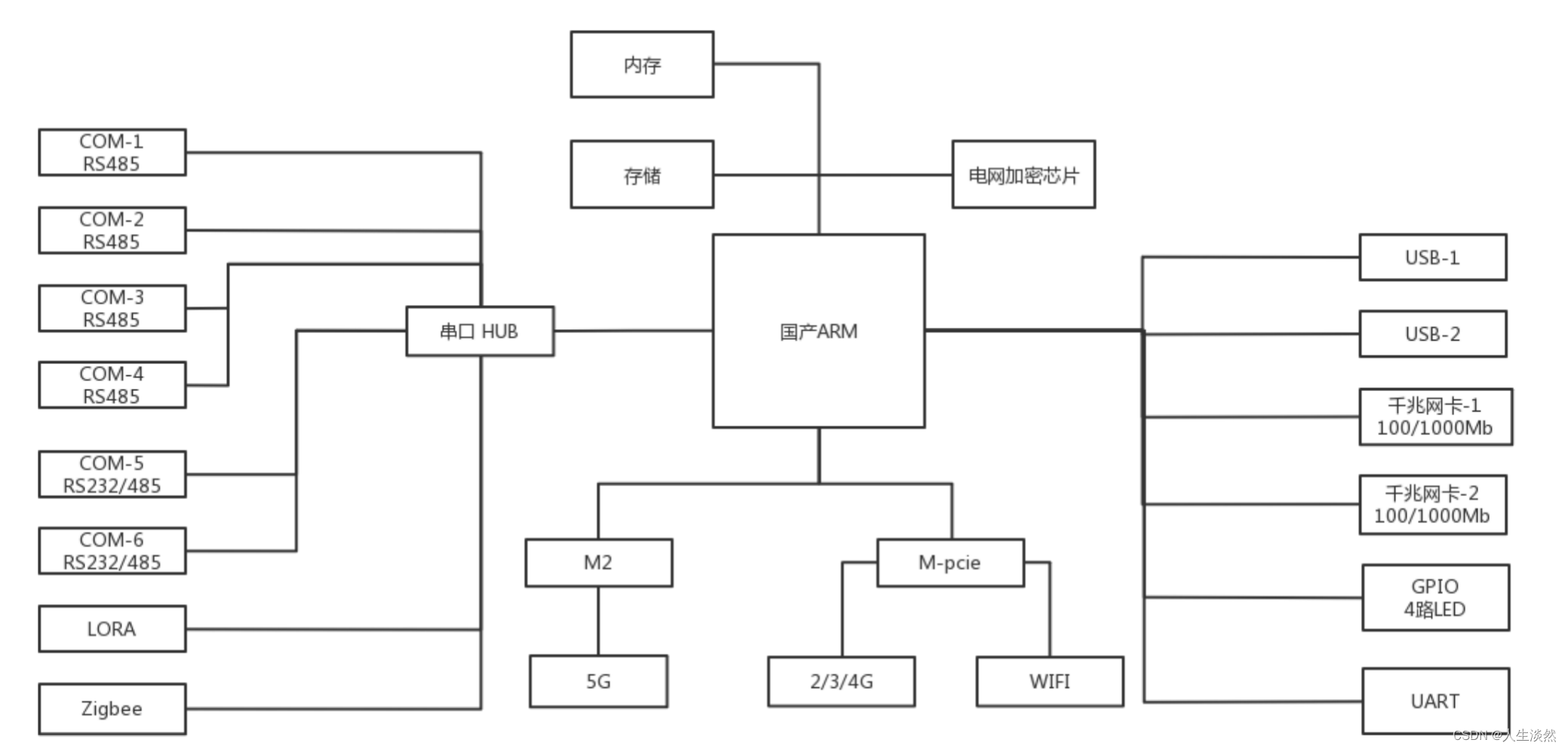
电力感知边缘计算技术网关产品设计方案-硬件方案
网关硬件架构设计图: 1.配置方案 配置差异 A类网关 B类网关 CPU...

【线性代数与矩阵论】坐标变换与相似矩阵
坐标变换与相似矩阵 2023年11月4日 #algebra 文章目录 坐标变换与相似矩阵1. 基变换与坐标变换2. 相似变换下链 1. 基变换与坐标变换 坐标变换与基变换都要通过过渡矩阵 A A A 来实现。设有一向量 f ⃗ \vec f f , x x x 是在基 α \alpha α 下该向量的坐标…...

C语言编译过程再解析
多年以前,分析过编译过程,并写了一篇博客,现在对编译过程有了更广阔的认识,记录在此 编译过程 中的 链接与 编译 编译过程分为1. 预处理2. 编译3. 汇编4. 链接其中有 2个过程比较特殊,1. 编译2. 链接对于C程序来说,链接分为提前链接(静态链接)对应下图第1行运行时链接(动态链…...
GeoTrust证书
GeoTrust证书的特点与优势: 1,广泛的浏览器兼容性: GeoTrust证书得到了各大主流浏览器的广泛支持,确保您的网站能够在用户使用的任何浏览器上获得正常的安全连接。 2,强大的加密技术: GeoTrust采用先进的…...
肾合胶囊 | 冬不养肾春易病,若出现了这六大表现,小心是肾虚!
冬季作为一年中最寒冷的季节,自然万物皆静谧闭藏,而肾具有潜藏、封藏、闭藏精气的特点,是封藏之本,肾的脏腑特性与冬季相通应,所以在冬季更应该重视养肾。 而现在正值初冬,正是开始养肾的最佳时间。此时培…...

IDEA中常用快捷键
整理了一些IDEA开发常用的快捷键: 快捷键组合实现效果psvm Tab键 / main Tab键public static void main(String[] args)sout Tab键System.out.println()Ctrl X删除当前行Ctrl D复制当前行AltInsert(或右键Generate)生成代码(如get,set方法,构造函数等)CtrlAltT…...

注解之@Configuration、@Bean、@Component
目录 前言 Component:通用的注解! Bean 引入第三方的类 Configuration 前言 首先:我们先简单描述一下这三个的作用 Component注解表明一个类会作为组件类,并告知Spring要为这个类创建bean。 Bean注解告诉Spring这个方法将会…...

【Web安全】sql注入绕过技法
sql注入绕过技法 1. 注释符号绕过 原理:SQL注释符号(如--, /* */)可以用来忽略查询的一部分,特别是在注入点之后的部分。这对于绕过需要闭合的查询或移除查询余下部分的情况特别有用。 -- 注释内容 # 注释内容 /*注释内容*/ ;2…...
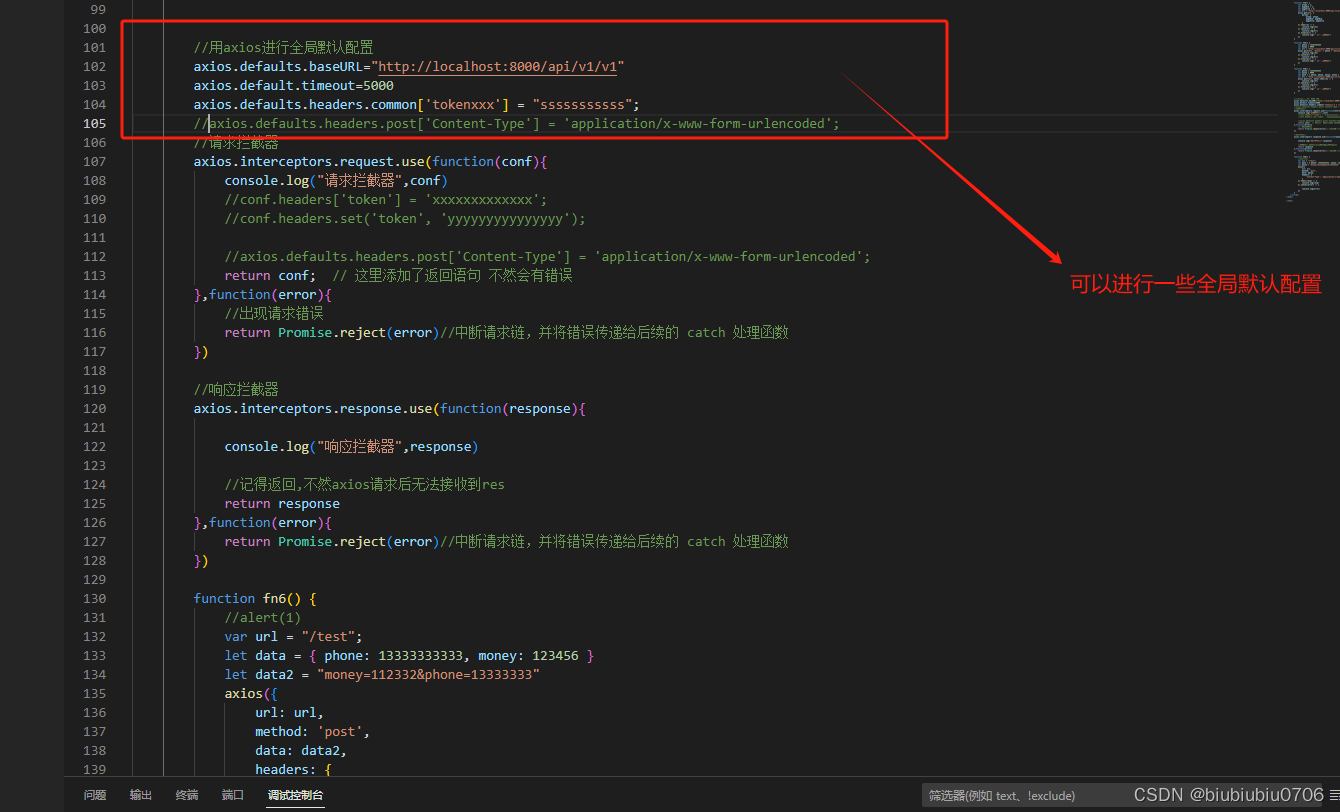
Axios使用方式
ajax是JQUERY封装的XMLHttprequest用来发送http请求 Axios简单点说它就是一个js库,支持ajax请求,发送axios请求功能更加丰富,丰富在哪不知道 1.npm使用方式 vue项目中 npm install axios 2.cdn方式 <script src"https://unpkg.com/axios/dist/axios.min.js">…...

kotlin 内置函数对数组进行各种操作
以下是一些常见的用法示例: plus() 函数将两个数组合并成一个数组。plus() 函数是 Kotlin 标准库中的一个扩展函数,可以用于合并两个同类型的数组。 fun main() {val array1 arrayOf(1, 2, 3)val array2 arrayOf(4, 5, 6)val mergedArray array1.plu…...

力扣labuladong——一刷day54
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣1660. 纠正二叉树二、力扣100. 相同的树三、力扣572. 另一棵树的子树四、力扣101. 对称二叉树 前言 判断树是否相等,就直接遍历就可以。判断…...

3、MSF使用
文章目录 一、利用ms17-010漏洞对靶机执行溢出攻击二、后渗透模块meterpreter的使用 一、利用ms17-010漏洞对靶机执行溢出攻击 分别输入以下命令,使用ms17_010_eternalblue模块对目标机的ms17-010漏洞进行利用: use exploit/windows/smb/ms17_010_eter…...

34970A 数据采集 / 数据记录仪开关单元
34970A 数据采集 / 数据记录仪开关单元 产品综述: Keysight 34970A 数据采集/数据记录仪开关单元由一个 3 插槽主机和一个内置的 6 1/2 位数字万用表组成。每个通道可以单独配置,以测量 11 种不同功能之一,这样既不会增加成本,也…...
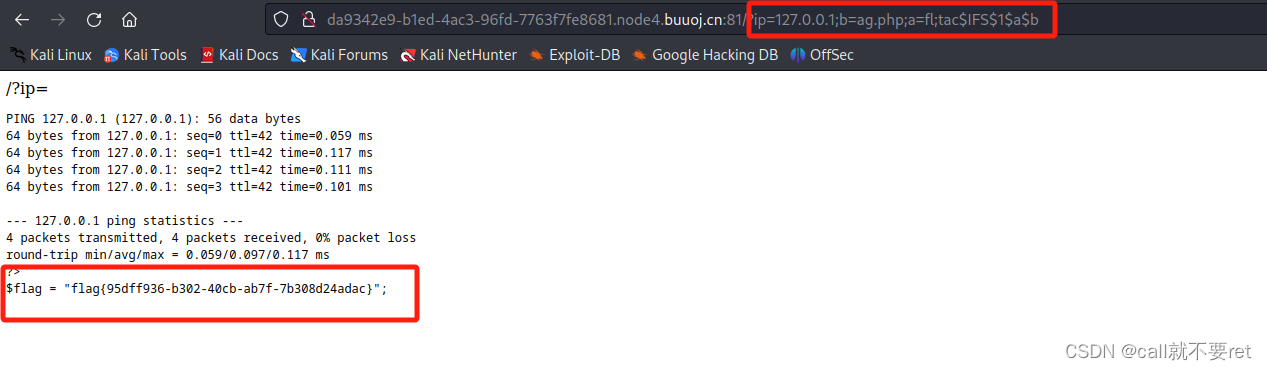
BUUCTF刷题之路-web-[GXYCTF2019]Ping Ping Ping1
启动环境后,是一个简简单单的页面: 看样子是能够触发远程执行漏洞的。尝试下ping 127.0.0.1,如果有回显说明我们的想法是对的。 最近才学习的nc反弹shell。想着是否能用nc反弹shell的办法。控制服务器然后输出flag呢?于是我测试下…...

一、深入简出串口(USRT)通信——基本概念。
一、前言 串口到底是什么?简单来说一句话就可以解释,串口就是一种通信协议。 看到这里可能大家会觉得你这不是放屁么,说了跟没说一样。所以这里做前言来描述,大家要先对通信协议有一个下意识地认识才能在学习串口的时候不至于迷茫…...
采用connector-c++ 8.0操作数据库
1.下载最新的Connector https://dev.mysql.com/downloads/connector/cpp/,下载带debug的库。 解压缩到本地,本次使用的是带debug模式的connector库: 注:其中mysqlcppconn与mysqlcppconn8的区别是: 2.在cmakelist…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
