【线性代数与矩阵论】坐标变换与相似矩阵
坐标变换与相似矩阵
2023年11月4日
#algebra
文章目录
- 坐标变换与相似矩阵
- 1. 基变换与坐标变换
- 2. 相似变换
- 下链
1. 基变换与坐标变换
坐标变换与基变换都要通过过渡矩阵 A A A 来实现。设有一向量 f ⃗ \vec f f , x x x 是在基 α \alpha α 下该向量的坐标, y y y 是在新基 β \beta β 下该向量的坐标,则基变换为:
β = α A , A = α − 1 β \beta=\alpha A \,\,,\,\, A= \alpha^ {-1} \beta β=αA,A=α−1β
式中的基也是矩阵。当原基 α = I \alpha= I α=I ,过渡矩阵的每一列列向量相当于新的坐标轴的基向量。
坐标变换通过原坐标向量左乘过渡矩阵的逆得到,即:
y = A − 1 x y= A^{-1}x y=A−1x
而注意,矩阵在某组基下的表示意味着相似变换。如矩阵 X X X 在基 β \beta β 下的表示为 Y Y Y,意味着
X β = β Y , Y = β − 1 X β X \beta=\beta Y \,\,,\,\, Y=\beta^{-1} X \beta Xβ=βY,Y=β−1Xβ
相当于矩阵的坐标变换,原基相当于单位阵。如果 X X X 又是矩阵 F F F 在某组基 α \alpha α 下的表示,则有
F α = α X , X = α − 1 F α F \alpha= \alpha X \,\,,\,\, X= \alpha^{-1}F \alpha Fα=αX,X=α−1Fα
Y = ( α − 1 β ) − 1 F ( α − 1 β ) = A − 1 F A Y=( \alpha^{-1} \beta)^{-1}F( \alpha^{-1} \beta)=A^{-1}FA Y=(α−1β)−1F(α−1β)=A−1FA
F F F 的基是单位阵。
2. 相似变换
如果存在可逆矩阵 P {P} P ,使得
B = P − 1 A P B=P^{-1}AP B=P−1AP
则称矩阵 A {A} A 与 B {B} B 相似,记为 A ∼ B {A\sim B} A∼B ;并称 P {P} P 为把 A {A} A 变成B的相似变换矩阵。显然相似即等价。
相似变换与逆矩阵有关,相似变换前后的矩阵为相似矩阵。
性质如下
- 反身性 A ∼ A A\sim A A∼A
- 对称性 A ∼ B → B ∼ A A\sim B\to B \sim A A∼B→B∼A
- 传递性 A ∼ B , B ∼ C → A ∼ C A\sim B \,\,,\,\, B\sim C\to A\sim C A∼B,B∼C→A∼C
几条定理,若 A ∼ B A\sim B A∼B
- rank ( A ) = rank ( B ) , ∣ A ∣ = ∣ B ∣ \text{rank}(A)= \text{rank}(B) \,\,,\,\, |A|=|B| rank(A)=rank(B),∣A∣=∣B∣
- det ( λ I − A ) = det ( λ I − B ) \det( \lambda I-A)=\det( \lambda I-B) det(λI−A)=det(λI−B),即特征相同
- A − 1 ∼ B − 1 , A T ∼ B T , f ( A ) ∼ f ( B ) A^{-1}\sim B^{-1} \,\,,\,\, A^ \mathrm T\sim B^ \mathrm T \,\,,\,\, f(A)\sim f(B) A−1∼B−1,AT∼BT,f(A)∼f(B)
说明
- 相似对角化 如果 A n {A_n} An 有 n {n} n 个线性无关的特征向量(特征值可以相同),则相似变换可以把 A {A} A 变成对角阵
- 实对称矩阵 A {A} A 可以相似对角化, rank ( A ) \text{rank}(A) rank(A) 等于非零特征值的个数
- 上/下三角矩阵主对角线元素相同则不能相似对角化
- n {n} n 阶方阵 A {A} A 满足的二次方程有两个互异实根,则因式分解后秩的和为 n {n} n ,且 A {A} A 可相似对角化
证明
A 2 − 3 A + 2 I = 0 → ( A − I ) ( A − 2 I ) = 0 A^2-3A+2I=0\to(A-I)(A-2I)=0 A2−3A+2I=0→(A−I)(A−2I)=0
∴ rank ( A − I ) + rank ( A − 2 I ) ≤ n \therefore \text{rank}(A-I)+ \text{rank}(A-2I) \le n ∴rank(A−I)+rank(A−2I)≤n
又 rank ( A − I ) + rank ( A − 2 I ) ≥ rank ( A − I + 2 I − A ) = rank ( I ) = n \text{又}\, \text{rank}(A-I)+ \text{rank}(A-2I)\ge \text{rank}(A-I+2I-A)= \text{rank}(I)=n 又rank(A−I)+rank(A−2I)≥rank(A−I+2I−A)=rank(I)=n
∴ rank ( A − I ) + rank ( A − 2 I ) = n \therefore \text{rank}(A-I)+ \text{rank}(A-2I)=n ∴rank(A−I)+rank(A−2I)=n
A {A} A 的线性无关特征向量的个数为
n − rank ( A − I ) + n − rank ( A − 2 I ) = 2 n − n = n n- \text{rank}(A-I)+ n- \text{rank}(A-2I)=2n-n=n n−rank(A−I)+n−rank(A−2I)=2n−n=n - 相似没有充要条件,有充分条件(矩阵有相同的相似对角化矩阵),也有必要条件(相似则1. 特征值相同 2. 秩相同)。如果特征值相同,而两个矩阵都不可对角化且秩相同,则不能判断矩阵是否相似。
使用相似变换求解LTI微分方程:
[!example]-
{ d d t x 1 = x 2 d d t x 2 = x 3 d d t x 3 = − 6 x 1 − 11 x 2 − 6 x 3 \begin{cases} \frac{\mathrm d}{\mathrm dt}x_1=x_2\\ \frac{\mathrm d }{\mathrm dt}x_2=x_3\\ \frac{\mathrm d }{\mathrm dt}x_3=-6x_1-11x_2-6x_3 \end{cases} ⎩ ⎨ ⎧dtdx1=x2dtdx2=x3dtdx3=−6x1−11x2−6x3
解:
A = [ 0 1 0 0 0 1 − 6 − 11 − 6 ] , det ( λ I − A ) = ( λ + 1 ) ( λ + 2 ) ( λ + 3 ) A= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -6 & -11 & -6 \end{bmatrix} \,\,,\,\, \det(\lambda I-A)=( \lambda+1)( \lambda+2)( \lambda+3) A= 00−610−1101−6 ,det(λI−A)=(λ+1)(λ+2)(λ+3)
有三个不同的特征值, A {A} A 可对角化。分别解 ( λ k I − A ) x = 0 , k = 1 , 2 , 3 (\lambda_k I-A)x=0 \,\,,\,\, k=1,2,3 (λkI−A)x=0,k=1,2,3,得变换矩阵
P = ( α 1 , α 2 , α 3 ) = [ 1 1 1 − 1 − 2 − 3 1 4 9 ] P=(\alpha_1,\alpha_2,\alpha_3)= \begin{bmatrix} 1 & 1 & 1 \\ -1 & -2 & -3 \\ 1 & 4 & 9 \end{bmatrix} P=(α1,α2,α3)= 1−111−241−39
D = P − 1 A P = [ − 1 0 0 0 − 2 0 0 0 − 3 ] D=P^{-1}AP= \begin{bmatrix} -1 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -3 \end{bmatrix} D=P−1AP= −1000−2000−3
由于 d d t x = A x \frac{\mathrm d }{\mathrm dt}x=Ax dtdx=Ax,令 x = P y x=Py x=Py,有
d y d t = P − 1 d x d t = P − 1 A x = P − 1 A P y = D y = [ − y 1 − 2 y 2 − 3 y 3 ] \frac{\mathrm d y}{\mathrm dt}=P^{-1} \frac{\mathrm d x}{\mathrm dt}=P^{-1}Ax=P^{-1}APy=Dy= \begin{bmatrix} -y_1\\-2y_2\\-3y_3 \end{bmatrix} dtdy=P−1dtdx=P−1Ax=P−1APy=Dy= −y1−2y2−3y3
y 1 ′ ( t ) = − y 1 , y 2 ′ ( t ) = − 2 y 2 , y 3 ′ ( t ) = − 3 y 3 y_1'(t)=-y_1 \,\,,\,\, y_2'(t)=-2y_2 \,\,,\,\, y_3'(t)=-3y_3 y1′(t)=−y1,y2′(t)=−2y2,y3′(t)=−3y3
y 1 ( t ) = c 1 e − t , y 2 ( t ) = c 2 e − 2 t , y 3 ( t ) = c 3 e − 3 t y_1(t)=c_1e^{-t} \,\,,\,\, y_2(t)=c_2e^{-2t} \,\,,\,\, y_3(t)=c_3e^{-3t} y1(t)=c1e−t,y2(t)=c2e−2t,y3(t)=c3e−3t
x = P y = [ c 1 e − t + c 2 e − 2 t + c 3 e − 3 t − c 1 e − t − 2 c 2 e − 2 t − 3 c 3 e − 3 t c 1 e − t + 4 c 2 e − 2 t + 9 c 3 e − 3 t ] x=Py= \begin{bmatrix} c_1e^{-t}+c_2e^{-2t}+ c_3e^{-3t}\\ -c_1e^{-t}-2c_2e^{-2t}-3c_3e^{-3t}\\ c_1e^{-t}+4c_2e^{-2t}+9 c_3e^{-3t} \end{bmatrix} x=Py= c1e−t+c2e−2t+c3e−3t−c1e−t−2c2e−2t−3c3e−3tc1e−t+4c2e−2t+9c3e−3t
下链
矩阵论 武汉理工大学 (亲测最好的矩阵论视频)
相关文章:

【线性代数与矩阵论】坐标变换与相似矩阵
坐标变换与相似矩阵 2023年11月4日 #algebra 文章目录 坐标变换与相似矩阵1. 基变换与坐标变换2. 相似变换下链 1. 基变换与坐标变换 坐标变换与基变换都要通过过渡矩阵 A A A 来实现。设有一向量 f ⃗ \vec f f , x x x 是在基 α \alpha α 下该向量的坐标…...

C语言编译过程再解析
多年以前,分析过编译过程,并写了一篇博客,现在对编译过程有了更广阔的认识,记录在此 编译过程 中的 链接与 编译 编译过程分为1. 预处理2. 编译3. 汇编4. 链接其中有 2个过程比较特殊,1. 编译2. 链接对于C程序来说,链接分为提前链接(静态链接)对应下图第1行运行时链接(动态链…...
GeoTrust证书
GeoTrust证书的特点与优势: 1,广泛的浏览器兼容性: GeoTrust证书得到了各大主流浏览器的广泛支持,确保您的网站能够在用户使用的任何浏览器上获得正常的安全连接。 2,强大的加密技术: GeoTrust采用先进的…...
肾合胶囊 | 冬不养肾春易病,若出现了这六大表现,小心是肾虚!
冬季作为一年中最寒冷的季节,自然万物皆静谧闭藏,而肾具有潜藏、封藏、闭藏精气的特点,是封藏之本,肾的脏腑特性与冬季相通应,所以在冬季更应该重视养肾。 而现在正值初冬,正是开始养肾的最佳时间。此时培…...

IDEA中常用快捷键
整理了一些IDEA开发常用的快捷键: 快捷键组合实现效果psvm Tab键 / main Tab键public static void main(String[] args)sout Tab键System.out.println()Ctrl X删除当前行Ctrl D复制当前行AltInsert(或右键Generate)生成代码(如get,set方法,构造函数等)CtrlAltT…...

注解之@Configuration、@Bean、@Component
目录 前言 Component:通用的注解! Bean 引入第三方的类 Configuration 前言 首先:我们先简单描述一下这三个的作用 Component注解表明一个类会作为组件类,并告知Spring要为这个类创建bean。 Bean注解告诉Spring这个方法将会…...

【Web安全】sql注入绕过技法
sql注入绕过技法 1. 注释符号绕过 原理:SQL注释符号(如--, /* */)可以用来忽略查询的一部分,特别是在注入点之后的部分。这对于绕过需要闭合的查询或移除查询余下部分的情况特别有用。 -- 注释内容 # 注释内容 /*注释内容*/ ;2…...
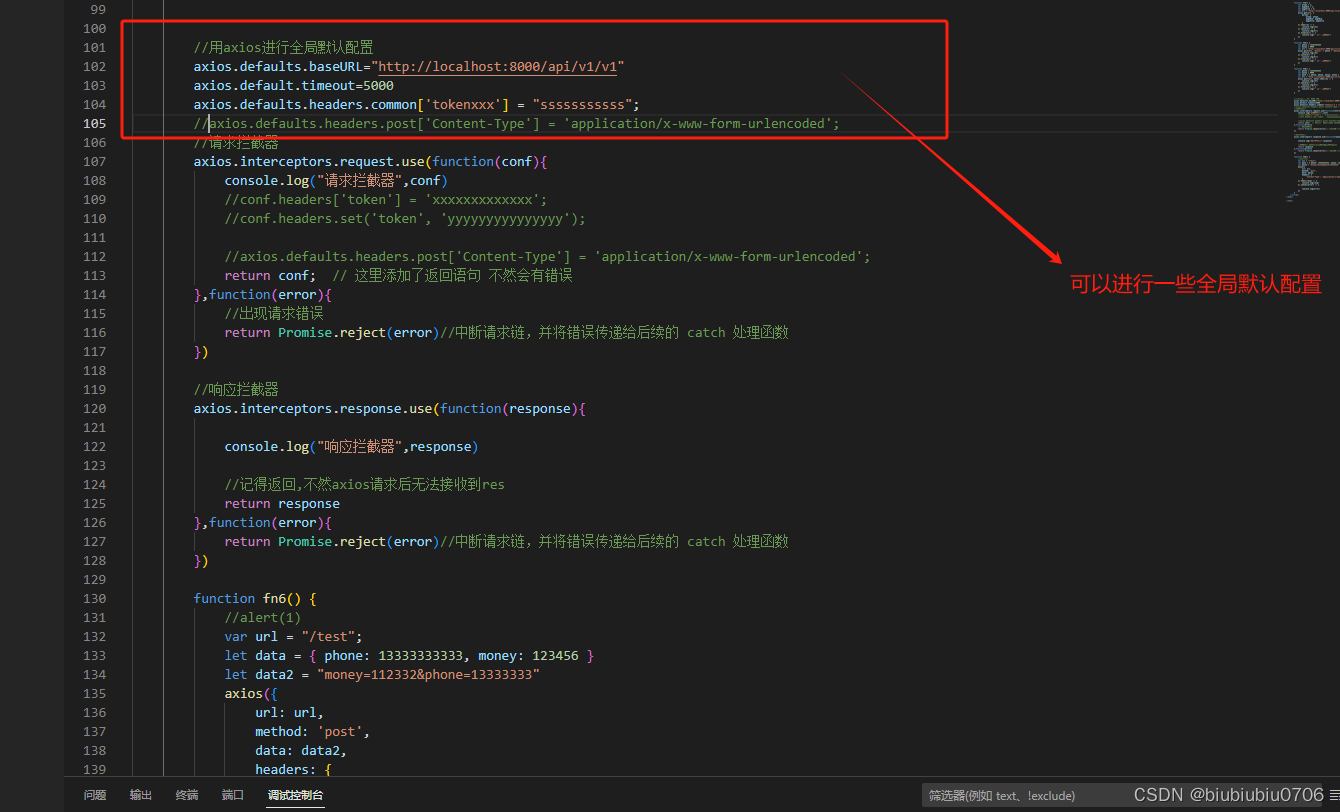
Axios使用方式
ajax是JQUERY封装的XMLHttprequest用来发送http请求 Axios简单点说它就是一个js库,支持ajax请求,发送axios请求功能更加丰富,丰富在哪不知道 1.npm使用方式 vue项目中 npm install axios 2.cdn方式 <script src"https://unpkg.com/axios/dist/axios.min.js">…...

kotlin 内置函数对数组进行各种操作
以下是一些常见的用法示例: plus() 函数将两个数组合并成一个数组。plus() 函数是 Kotlin 标准库中的一个扩展函数,可以用于合并两个同类型的数组。 fun main() {val array1 arrayOf(1, 2, 3)val array2 arrayOf(4, 5, 6)val mergedArray array1.plu…...

力扣labuladong——一刷day54
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣1660. 纠正二叉树二、力扣100. 相同的树三、力扣572. 另一棵树的子树四、力扣101. 对称二叉树 前言 判断树是否相等,就直接遍历就可以。判断…...

3、MSF使用
文章目录 一、利用ms17-010漏洞对靶机执行溢出攻击二、后渗透模块meterpreter的使用 一、利用ms17-010漏洞对靶机执行溢出攻击 分别输入以下命令,使用ms17_010_eternalblue模块对目标机的ms17-010漏洞进行利用: use exploit/windows/smb/ms17_010_eter…...

34970A 数据采集 / 数据记录仪开关单元
34970A 数据采集 / 数据记录仪开关单元 产品综述: Keysight 34970A 数据采集/数据记录仪开关单元由一个 3 插槽主机和一个内置的 6 1/2 位数字万用表组成。每个通道可以单独配置,以测量 11 种不同功能之一,这样既不会增加成本,也…...
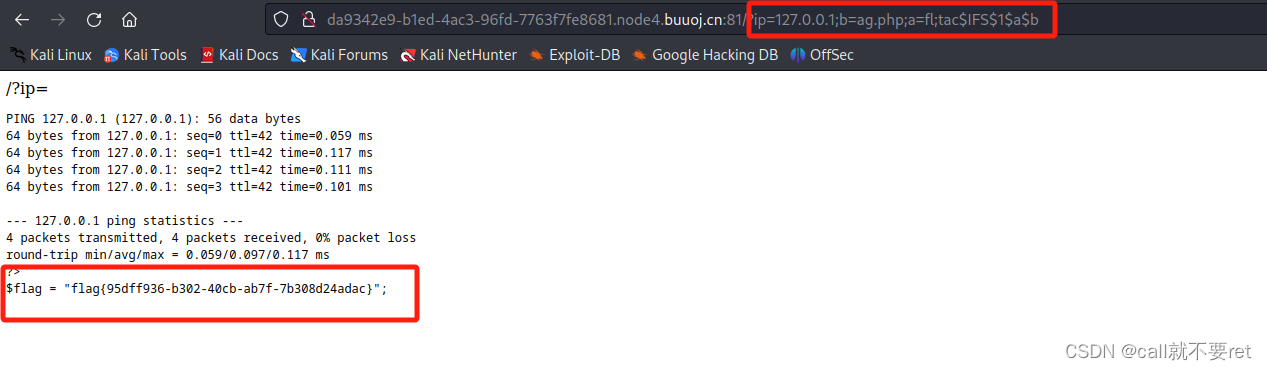
BUUCTF刷题之路-web-[GXYCTF2019]Ping Ping Ping1
启动环境后,是一个简简单单的页面: 看样子是能够触发远程执行漏洞的。尝试下ping 127.0.0.1,如果有回显说明我们的想法是对的。 最近才学习的nc反弹shell。想着是否能用nc反弹shell的办法。控制服务器然后输出flag呢?于是我测试下…...

一、深入简出串口(USRT)通信——基本概念。
一、前言 串口到底是什么?简单来说一句话就可以解释,串口就是一种通信协议。 看到这里可能大家会觉得你这不是放屁么,说了跟没说一样。所以这里做前言来描述,大家要先对通信协议有一个下意识地认识才能在学习串口的时候不至于迷茫…...
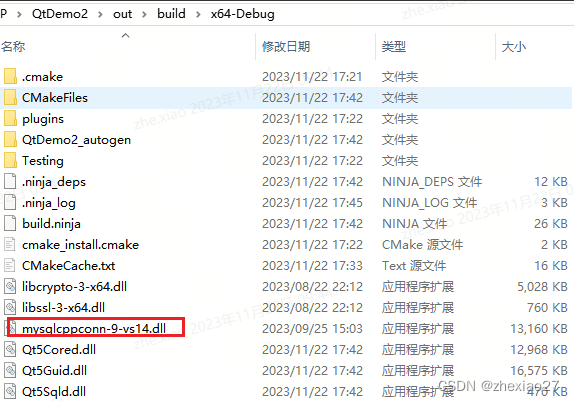
采用connector-c++ 8.0操作数据库
1.下载最新的Connector https://dev.mysql.com/downloads/connector/cpp/,下载带debug的库。 解压缩到本地,本次使用的是带debug模式的connector库: 注:其中mysqlcppconn与mysqlcppconn8的区别是: 2.在cmakelist…...

【Java数据结构 -- 时间和空间复杂度】
时间和空间复杂度 1. 算法效率2. 时间复杂度2.1 时间复杂度的概念2.2 大O的渐进表示法2.3 推导大O阶方法2.4 常见时间复杂度计算举例例1例2例3例4 计算 bubbleSort的时间复杂度例5 计算binarySearch的时间复杂度?例6 计算阶乘递归factorial的时间复杂度?…...

【每日一题】1457. 二叉树中的伪回文路径-2023.11.25
题目: 1457. 二叉树中的伪回文路径 给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。 请你返回从根到叶子节点的所有路…...

能让PDF看起来像是扫描件的Look Scanned
什么是 Look Scanned ? Look Scanned 是一个能够让 PDF 看起来就像是扫描件一样的纯前端网站。你再也不需要麻烦地打印之后扫描了,你所需要的就是鼠标点几下。 这是个挺有意思的软件,但是老苏不确定什么场景下会用到这个软件,如果不想自己搭…...

RT-DETR 更换损失函数之 SIoU / EIoU / WIoU / Focal_xIoU
文章目录 更换方式CIoUDIoUEIoUGIoUSIoUWIoUFocal_CIoUFocal_DIoUFocal_EIoUFocal_GIoUFocal_SIoU提示更换方式 第一步:将ultralytics/ultralytics/utils/metrics.py文件中的bbox_iou替换为如下的代码:class...

代码随想录算法训练营第四十六天 | 139.单词拆分,多重背包,背包问题总结
目录 139.单词拆分 多重背包 背包问题总结 01背包 完全背包 多重背包 139.单词拆分 题目链接:139. 单词拆分 不要求字典中的单词全部使用,但是要求拆分的单词拆分成的每一个子串都是字典中的单词。 (1)dp[ i ] 表示前 i 个字符组成…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
