【Java数据结构 -- 时间和空间复杂度】
时间和空间复杂度
- 1. 算法效率
- 2. 时间复杂度
- 2.1 时间复杂度的概念
- 2.2 大O的渐进表示法
- 2.3 推导大O阶方法
- 2.4 常见时间复杂度计算举例
- 例1
- 例2
- 例3
- 例4 计算 bubbleSort的时间复杂度
- 例5 计算binarySearch的时间复杂度?
- 例6 计算阶乘递归factorial的时间复杂度?
- 例7 计算斐波那契递归fibonacci的时间复杂度?
- 3. 空间复杂度
- 例1 计算bubbleSort的空间复杂度?
- 例2 计算fibonacci的空间复杂度?
- 例3 计算阶乘递归Factorial的空间复杂度?
- 4. 总结
1. 算法效率
算法效率分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称作空间复杂度。时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间,在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
2. 时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度,即一个算法的运行时间和这个算法当中的语句执行次数有关系,语句执行次数越多,运行时间就多,成正比的一个关系。
2.2 大O的渐进表示法
// 请计算一下func1基本操作执行了多少次?//F(N) = n^2 + 2n + 10 O(n^2)void func1(int N) {int count = 0;for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++; //n+n+n+...+n 即n*n=n^2}}for (int k = 0; k < 2 * N; k++) {count++; //2n}int M = 10;while ((M--) > 0) {count++; //10}System.out.println(count);}
Func1执行的基本操作次数:
F(N) = N^2 + 2*N + 10
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号(Big O notation):是用于描述函数渐进行为的数学符号
2.3 推导大O阶方法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,即随着N越来越大时 10和2*n会很小可以省略,Func1的时间复杂度为:O(N^2)
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
2.4 常见时间复杂度计算举例
时间复杂度的计算需要配合逻辑来看的
例1
// 计算func2的时间复杂度?//F(N) = 2n + 10 O(N)=nvoid func2(int N) {int count = 0;for (int k = 0; k < 2 * N ; k++) {count++; // 2n}int M = 10;while ((M--) > 0) {count++; //10}System.out.println(count);}
例2
// 计算func3的时间复杂度?// n+m = O(n+m)void func3(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++; //m}for (int k = 0; k < N ; k++) {count++; //n}System.out.println(count);}
例3
// 计算func4的时间复杂度?// O(1)void func4(int N) {int count = 0;for (int k = 0; k < 100; k++) {count++; // 100}System.out.println(count);}
例4 计算 bubbleSort的时间复杂度
O(n^2),而在最好情况下就是原本就是已经排好的顺序,O(n)
// 计算bubbleSort的时间复杂度?//F(N)=(1+n-1)*(n-1)/2 = 1/2*n^2 - 1/2*n = n^2 即O(n^2)void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) { //Nboolean sorted = true;for (int i = 1; i < end; i++) { // n-1 + n-2 + ..+2+1//即当end的值不一样 执行的次数也不一样 (1+n-1)*(n-1)/2if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}private void Swap(int[] array, int i, int i1) {}
例5 计算binarySearch的时间复杂度?
二分查找 一次砍一半 --> n n/2 n/4 … 1 即n/2^x=1 --> n=2^x 即log2^n
O(log2^n)
// 计算binarySearch的时间复杂度?// 二分查找 一次砍一半 --> n n/2 n/4 ... 1 即n/2^x=1 --> n=2^x 即log2^n// O(log2^n)int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1; //n-1while (begin <= end) {int mid = begin + ((end-begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;}
例6 计算阶乘递归factorial的时间复杂度?
递归的时间复杂度 = 递归的次数 * 每次递归后执行的次数
O(n)
// 计算阶乘递归factorial的时间复杂度?// 递归的时间复杂度 = 递归的次数 * 每次递归后执行的次数// O(n)long factorial(int N) { // n// 三目运算符不是循环 是一个判断 执行的次数是1return N < 2 ? N : factorial(N-1) * N;}
例7 计算斐波那契递归fibonacci的时间复杂度?
F(N) -> F(N-1) F(N-2) -> F(N-2) F(N-3) F(N-3) F(N-4)
1+2+4+...+2^(n-1) = 2^(n-1)-1 即 O(2^n)
O(2^n)
// 计算斐波那契递归fibonacci的时间复杂度?// F(N) -> F(N-1) F(N-2) -> F(N-2) F(N-3) F(N-3) F(N-4)// 2^0=1 2^1=2 2^2=4 ... 2^(n-1)// 1+2+4+...+2^(n-1) = 2^(n-1)-1 即 O(2^n)int fibonacci(int N) {return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);}3. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
例1 计算bubbleSort的空间复杂度?
O(1)
// 计算bubbleSort的空间复杂度?// 有临时变量 没有申请其它数组 O(1)void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}}private void Swap(int[] array, int i, int i1) {}
例2 计算fibonacci的空间复杂度?
// 计算fibonacci的空间复杂度?// 动态开辟了N个空间// O(n)long[] fibonacci(int n) {long[] fibArray = new long[n + 1]; // 重新申请了一个数组来存放数据fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; i++) {fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}
例3 计算阶乘递归Factorial的空间复杂度?
// 计算阶乘递归Factorial的空间复杂度?// 递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间 O(n)long factorial(int N) {return N < 2 ? N : factorial(N-1)*N;}
4. 总结
- 结合代码的实现去做 空间和时间复杂度的计算
- 一些常用的复杂度大小:
O(1) < O(log2^n) < O(n) < O(n*log2的n次) < O(n的平方)
相关文章:

【Java数据结构 -- 时间和空间复杂度】
时间和空间复杂度 1. 算法效率2. 时间复杂度2.1 时间复杂度的概念2.2 大O的渐进表示法2.3 推导大O阶方法2.4 常见时间复杂度计算举例例1例2例3例4 计算 bubbleSort的时间复杂度例5 计算binarySearch的时间复杂度?例6 计算阶乘递归factorial的时间复杂度?…...

【每日一题】1457. 二叉树中的伪回文路径-2023.11.25
题目: 1457. 二叉树中的伪回文路径 给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。 请你返回从根到叶子节点的所有路…...

能让PDF看起来像是扫描件的Look Scanned
什么是 Look Scanned ? Look Scanned 是一个能够让 PDF 看起来就像是扫描件一样的纯前端网站。你再也不需要麻烦地打印之后扫描了,你所需要的就是鼠标点几下。 这是个挺有意思的软件,但是老苏不确定什么场景下会用到这个软件,如果不想自己搭…...

RT-DETR 更换损失函数之 SIoU / EIoU / WIoU / Focal_xIoU
文章目录 更换方式CIoUDIoUEIoUGIoUSIoUWIoUFocal_CIoUFocal_DIoUFocal_EIoUFocal_GIoUFocal_SIoU提示更换方式 第一步:将ultralytics/ultralytics/utils/metrics.py文件中的bbox_iou替换为如下的代码:class...

代码随想录算法训练营第四十六天 | 139.单词拆分,多重背包,背包问题总结
目录 139.单词拆分 多重背包 背包问题总结 01背包 完全背包 多重背包 139.单词拆分 题目链接:139. 单词拆分 不要求字典中的单词全部使用,但是要求拆分的单词拆分成的每一个子串都是字典中的单词。 (1)dp[ i ] 表示前 i 个字符组成…...
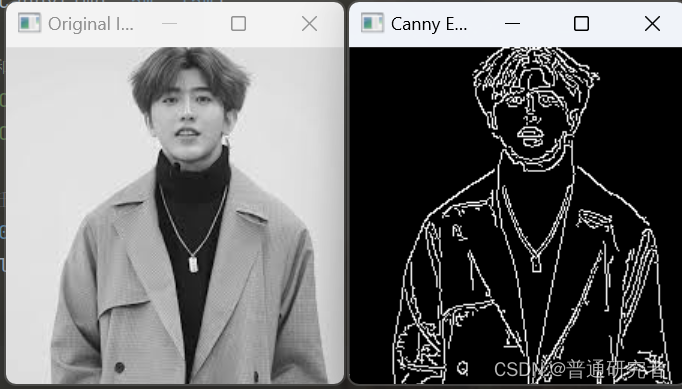
opencv-Canny 边缘检测
Canny边缘检测是一种经典的图像边缘检测算法,它在图像中找到强度梯度的变化,从而识别出图像中的边缘。Canny边缘检测的优点包括高灵敏度和低误检率。 在OpenCV中,cv2.Canny() 函数用于执行Canny边缘检测。 基本语法如下: edges…...

案例023:基于微信小程序的童装商城的设计与实现
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

Ansible的循环:loop,with_<lookup>和until
环境 管理节点:Ubuntu 22.04控制节点:CentOS 8Ansible:2.15.6 循环的方法 loopwith_<lookup>until 用这几种方式都可以实现循环。其中, loop 是推荐的用法,在很多时候能够替换 with_<lookup> 。 loop…...

点云 surface 方法总结
点云的表面方法是指通过点云数据来估计和重建物体或场景的表面几何形状。下面总结了几种常见的点云表面方法: 三角化:三角化是最常用的点云表面重建方法之一。它将点云中的点连接成三角形网格,从而重建出物体或场景的表面。常见的三角化算法…...

深入探索Linux文件系统:属性、路径与隐藏之谜
🎥 屿小夏 : 个人主页 🔥个人专栏 : Linux系统理论 🌄 莫道桑榆晚,为霞尚满天! 文章目录 📑前言🌤️文件的组成☁️文件属性☁️文件内容☁️注意事项 🌤️路…...
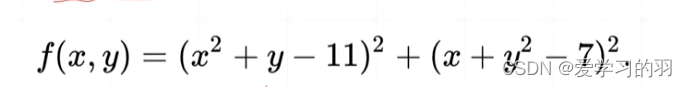
梯度详解与优化实战
什么是梯度 对所有自变量求偏微分构成的向量,它是一个向量(有大小和函数值增长方向) 导数是一个标量 找最小值点坐标的案例 import torchimport numpy as np import matplotlib.pyplot as plt def himmelblau(x):return (x[0]**2x[1]-11)…...

OSG编程指南<十二>:OSG二三维文字创建及文字特效
1、字体基础知识 适当的文字信息对于显示场景信息是非常重要的。在 OSG 中,osgText提供了向场景中添加文字的强大功能,由于有第三方插件 FreeType 的支持,它完全支持TrueType 字体。很多人可能对 FreeType 和 TrueType 还不太了解,…...
visionOS空间计算实战开发教程Day 6 拖拽和点击
在之前的学习中我们在空间中添加了3D模型,但在初始摆放后就无法再对其进行移动或做出修改。本节我们在Day 5显示和隐藏的基础上让我们模型可以实现拖拽效果,同时对纯色的立方体实现点击随机换色的功能。 首先是入口文件,无需做出改变…...
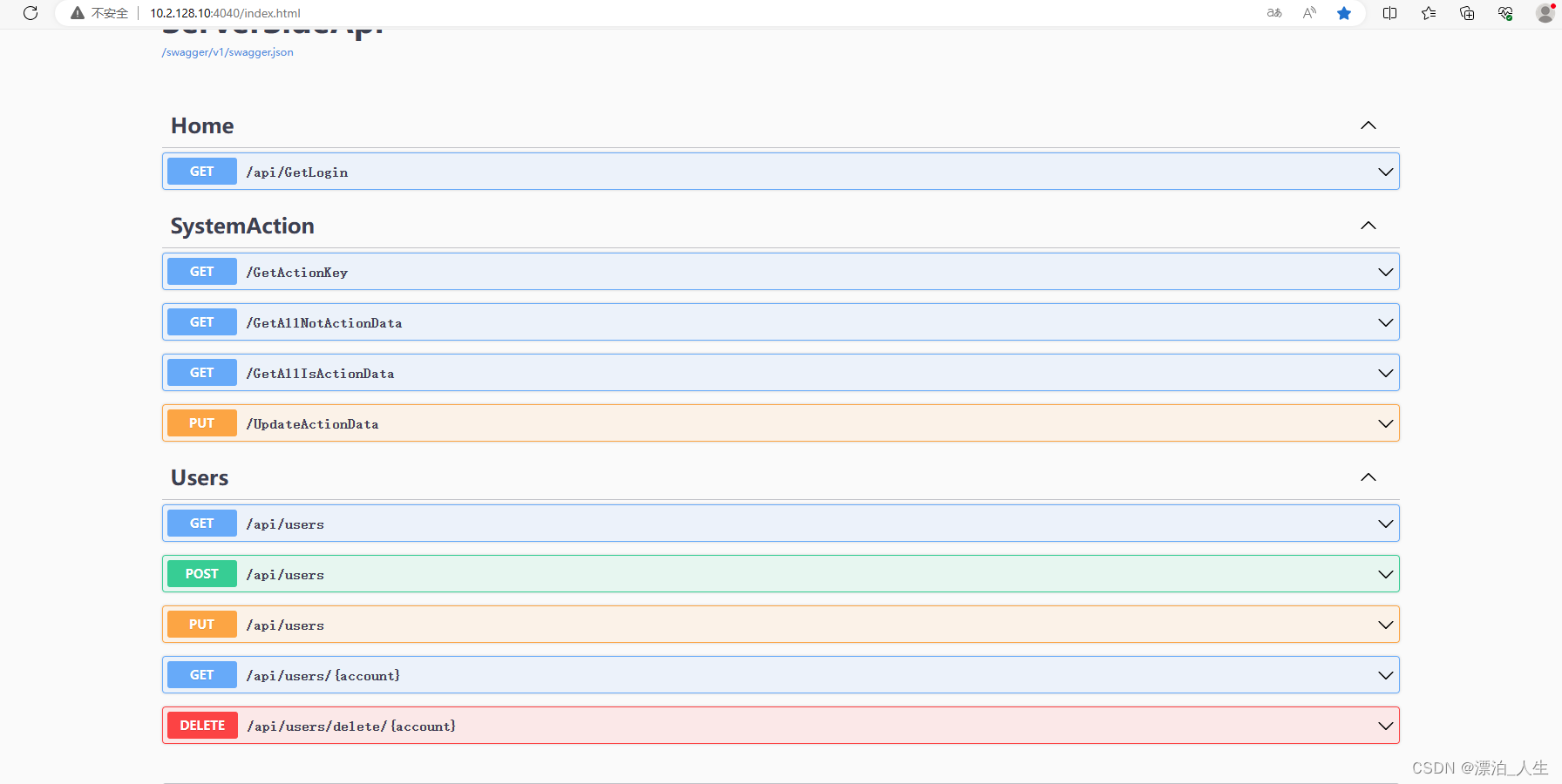
C# APS.NET CORE 6.0 WEB API IIS部署
1.创建 APS.NET CORE6.0 WEB API项目 默认选项即可 源代码: 项目文件展开: launchSettings.json {"$schema": "https://json.schemastore.org/launchsettings.json","iisSettings": {"windowsAuthentication"…...
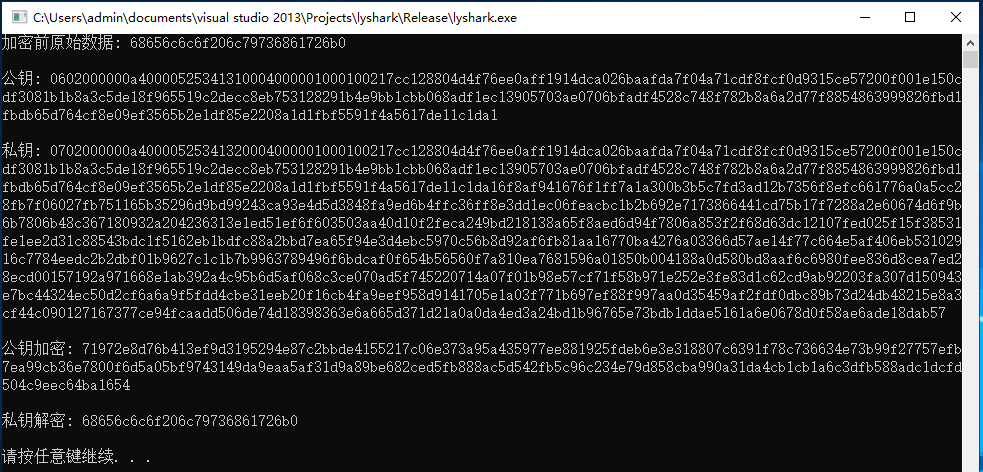
C/C++ 常用加密与解密算法
计算机安全和数据隐私是现代应用程序设计中至关重要的方面。为了确保数据的机密性和完整性,常常需要使用加密和解密算法。C是一种广泛使用的编程语言,提供了许多加密和解密算法的实现。本文将介绍一些在C中常用的加密与解密算法,这其中包括Xo…...

从Qt源码的角度分析Qt对象树与内存管理模式
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 一、Qt对象树(Object Tree)和父子关系二、源码角度:QObject的内存管理构造函数析构函数addChild() 和 removeChild()三、C++模拟实现Qt的对象树内存管理模式Qt框架提供了一…...

MySQL与Redis如何保证数据的一致性
文章目录 MySQL与Redis如何保证数据的一致性?不好的方案1. 先写 MySQL,再写 Redis2. 先写 Redis,再写 MySQL3. 先删除 Redis,再写 MySQL 好的方案4. 先删除 Redis,再写 MySQL,再删除 Redis5. 先写 MySQL&am…...

micropython - espnow
espnow这个东西可以很简单的进行多设备近距离互联,连握手都不用注册一下就能发信息 目前8266那个8角的刷20231105的1M的固件可以运行 8266目前没有信号强度功能所以我自己写的类强度返回为0 我写的类实例化后最后注册谁发消息就是给谁而接收端则是什么都接ÿ…...
京东数据采集(京东数据运营):怎样快速获取京东市场大数据?
相信京东平台的很多品牌方们都有做数据分析的需求,但面对多而杂的市场数据,很多运营者都没有思路。单依靠肉眼来看,很多商品的类目、销售成绩、价格分布等运营者也未必清楚。 其实对于京东平台上市场数据的获取,品牌可以直接借助一…...

重生奇迹mu迷宫攻略
重生奇迹mu迷宫是一种比较有挑战性的游戏玩法,需要一定的技巧和策略才能完成。以下是一些基本的攻略和技巧: 了解每个迷宫的特点:不同的迷宫有不同的规则和特点,需要根据迷宫的特点来制定合理的策略。在进入迷宫前可以先了解一下…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
