FO-like Transformation
参考文献:
- [RS91] Rackoff C, Simon D R. Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack[C]//Annual international cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991: 433-444.
- [BR93] Bellare M, Rogaway P. Random oracles are practical: A paradigm for designing efficient protocols[C]//Proceedings of the 1st ACM Conference on Computer and Communications Security. 1993: 62-73.
- [FO99] Fujisaki, Eiichiro, and Tatsuaki Okamoto. “Secure integration of asymmetric and symmetric encryption schemes.” Annual international cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 1999.
- [OP01] Okamoto T, Pointcheval D. REACT: Rapid enhanced-security asymmetric cryptosystem transform[C]//Topics in Cryptology—CT-RSA 2001: The Cryptographers’ Track at RSA Conference 2001 San Francisco, CA, USA, April 8–12, 2001 Proceedings. Springer Berlin Heidelberg, 2001: 159-174.
- [CS03] Cramer R, Shoup V. Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack[J]. SIAM Journal on Computing, 2003, 33(1): 167-226.
- [Dent03] Dent A W. A designer’s guide to KEMs[C]//IMA International Conference on Cryptography and Coding. Berlin, Heidelberg: Springer Berlin Heidelberg, 2003: 133-151.
- [FO13] Fujisaki E, Okamoto T. Secure integration of asymmetric and symmetric encryption schemes[J]. Journal of cryptology, 2013, 26: 80-101.
- [HHK17] Hofheinz D, Hövelmanns K, Kiltz E. A modular analysis of the Fujisaki-Okamoto transformation[C]//Theory of Cryptography Conference. Cham: Springer International Publishing, 2017: 341-371.
- [AOP+17] Albrecht M R, Orsini E, Paterson K G, et al. Tightly secure ring-LWE based key encapsulation with short ciphertexts[C]//Computer Security–ESORICS 2017: 22nd European Symposium on Research in Computer Security, Oslo, Norway, September 11-15, 2017, Proceedings, Part I 22. Springer International Publishing, 2017: 29-46.
- PKE 安全性的提升方式:Naor-Yung、Fischlin、Fujisaki-Okamoto
- 量子计算:基本概念
文章目录
- KEM & DEM
- Security
- Correctness
- OW & IND
- PCA & VA & PCVA
- QROM
- Fine-Grained FO
- T 变换
- U 变换
- FO-like KEM
- QU 变换
- Quantum KEM
- S 变换
- Reduce RLWE to IND-CCA
KEM & DEM
[RS91] 给出了 IND-CCA 安全的概念,[BR93] 给出了 ROM 的设计范式。
[CS03] 最先提出了基于 KEM(Asymmetrickey Key Encapsulation Mechanism)和 DEM(Symmetric Data Encapsulation Mechanism)构造出 hybrid constructions 的设计思路。[CS03] 指出,任意的 IND-CCA KEM(比 PKE 更弱)组合上任意的 One-time CCA DEM(对称加密),需要它们的安全属性相互独立,那么就得到了一个 IND-CCA PKE
但是 IND-CCA KEM 通常难以构造(直接归约到底层困难问题是很麻烦的),因此人们往往先构造 IND-CPA KEM,然后再利用某些转换方案得到 IND-CCA KEM
一般地,我们直接将 General-Purpose PKE 作为 KEM 来使用,但是也许可能直接实现 KEM 会更加高效。
之后的 [Dent03] 推广和提出了一些简单高效的 IND-CCA KEM 构造,其中包括了 KEM 版本 FO 和 REACT/GEM 的现代化描述。
Security
[HHK17] 研究了 FO-like,发现目前唯一的从 CPA 安全提升到 IND-CCA 安全的手段,实际上就只有 FO 转换(及其变体)。另外,[FO13] 的归约不紧,并且需要底层 PKE 解密无差错,以及一些其他的更强要求。[HHK17] 给出了从 CPA 到 CCA 的更细粒度转换方案,归约中考虑了解密差错的鲁棒性,将它们相互组合可以得到多种 FO 变体。因此我们先给出一些的安全性描述。
Correctness
原始 [FO99] [FO13] 以及其他变体的缺陷:
- 在 FO 和 REACT/GEM 的归约中,要求底层 PKE 的解密是完美正确的(perfect correct)。但是 LWE-based PKE 不可避免地引入噪声,导致存在解密失败的情况。
- 另外,原始 FO 转换的归约是不紧的;REACT/GEM 转换的归约是紧的,但它要求底层 PKE 是 OW-PCA 安全。由于 D-LWE 和 S-LWE 的等价性,导致了许多自然的格密码方案不能够达到 OW-PCA 安全 。
[HHK17] 解释说已有的格密码方案的解密正确性的定义有些微妙,因此他们使用了一种精心挑选的定义,使得它既符合 FO 归约需要,又使得所有格密码也都满足这个定义。
正确性(Correctness):我们称某个 PKE 是 δ \delta δ-correct,如果它满足
E ( s k , p k ) ← G e n ( 1 λ ) [ max m ∈ M Pr r ← R [ D e c ( s k , c ) ≠ m ∣ c ← E n c ( p k , m ; r ) ] ] ≤ δ \underset{(sk,pk)\gets Gen(1^\lambda)}{\mathbb E} \left[ \max_{m \in M} \underset{r \gets R}{\Pr}[Dec(sk,c) \neq m \mid c \gets Enc(pk,m;r)] \right] \le \delta (sk,pk)←Gen(1λ)E[m∈Mmaxr←RPr[Dec(sk,c)=m∣c←Enc(pk,m;r)]]≤δ
这个期望是关于 ( s k , p k ) (sk,pk) (sk,pk) 的,而每一个确定的公私钥对,对于每一个消息 m m m,都有关于随机带 r r r 的解密失败概率。
或者更方便地,可以将它基于游戏来定义:

对于任意的(无界)敌手 A A A,使得:
Pr [ C O R P K E A → 1 ] ≤ δ \Pr[COR_{PKE}^A \to 1] \le \delta Pr[CORPKEA→1]≤δ
对于 RO Model,假如敌手可以访问随机神谕 G , H , ⋯ G,H,\cdots G,H,⋯(若干个),查询次数限制为 q G , q H , ⋯ q_G,q_H,\cdots qG,qH,⋯,那么就有:
Pr [ C O R - R O P K E A → 1 ] ≤ δ ( q G , q H , ⋯ ) \Pr[COR\text-RO_{PKE}^A \to 1] \le \delta(q_G,q_H,\cdots) Pr[COR-ROPKEA→1]≤δ(qG,qH,⋯)
Standard Model 可以视为 RO Model 的特殊情况(没有 q G q_G qG 等输入),函数 δ ( q G , q H , ⋯ ) \delta(q_G,q_H,\cdots) δ(qG,qH,⋯) 成为了某个常数 δ \delta δ
有效密文(valid ciphertext):解密函数 D e c Dec Dec 检查密文是否是有效的,对于无效密文,输出特殊符号 ⊥ ∉ M \perp \notin M ⊥∈/M 表示拒绝。
单射性(Injectivity):对于所有的 ( s k , p k ) ← G e n (sk,pk) \gets Gen (sk,pk)←Gen,总是有
E n c ( p k , m ; r ) = E n c ( p k , m ′ ; r ′ ) ⟹ ( m , r ) = ( m ′ , r ′ ) , ∀ m , m ′ ∈ M , r , r ′ ∈ R Enc(pk,m;r) = Enc(pk,m';r') \Longrightarrow (m,r)=(m',r'),\,\, \forall m,m'\in M,r,r'\in R Enc(pk,m;r)=Enc(pk,m′;r′)⟹(m,r)=(m′,r′),∀m,m′∈M,r,r′∈R
也就是说,函数 E n c ( p k , ⋯ ) : M × R → C Enc(pk,\cdots):M \times R \to C Enc(pk,⋯):M×R→C 是单射,必要条件是 ∣ C ∣ ≥ ∣ M ∣ ⋅ ∣ R ∣ |C| \ge |M| \cdot |R| ∣C∣≥∣M∣⋅∣R∣ 足够大。此时,每个有效密文都只能解密出唯一的消息,以及唯一的随机带。
刚性(Rigidity):这是针对确定性 PKE 的,对于所有的 ( s k , p k ) ← G e n (sk,pk) \gets Gen (sk,pk)←Gen,总是有
D e c ( s k , c ) = ⊥ or E n c ( p k , D e c ( s k , c ) ) = c Dec(sk,c) = \perp \text{ or } Enc(pk,Dec(sk,c)) = c Dec(sk,c)=⊥ or Enc(pk,Dec(sk,c))=c
也就是说,除了非法的密文,有效密文总是可以解密出正确的消息,不存在解密错误。注意区分:拒绝(识别非法密文并输出特殊符号)、失败(解密出的结果与原始消息不一致)。
γ \gamma γ-Spread:我们定义密文 E n c ( p k , m ; r ) Enc(pk,m;r) Enc(pk,m;r) 的最小熵
γ ( p k , m ) : = − log max c ∈ C Pr r ← R [ E n c ( p k , m ; r ) = c ] \gamma(pk,m) := -\log\max_{c \in C} \underset{r \gets R}{\Pr}[Enc(pk,m;r)=c] γ(pk,m):=−logc∈Cmaxr←RPr[Enc(pk,m;r)=c]
如果存在常数 γ \gamma γ ,满足 γ ( p k , m ) ≥ γ , ∀ ( p k , s k ) ← G e n , ∀ m ∈ M \gamma(pk,m) \ge \gamma,\,\, \forall(pk,sk)\gets Gen,\,\, \forall m \in M γ(pk,m)≥γ,∀(pk,sk)←Gen,∀m∈M。这直接导致了
Pr r ← R [ E n c ( p k , m ; r ) = c ] ≤ 2 − γ , ∀ c ∈ C \underset{r \gets R}{\Pr}[Enc(pk,m;r) = c] \le 2^{-\gamma},\,\, \forall c \in C r←RPr[Enc(pk,m;r)=c]≤2−γ,∀c∈C
即对于固定的 ( s k , p k ) (sk,pk) (sk,pk) 和 m m m,随机带 r r r 使得此消息的加密是高熵的。
OW & IND
One-Way 安全性(OW):这是比 IND 更强的攻击目标,要求敌手根据密文 c ∗ ← E n c ( p k , m ∗ ; r ) c^* \gets Enc(pk,m^*;r) c∗←Enc(pk,m∗;r),找出消息 m ′ ∈ M m' \in M m′∈M,满足 m ′ = D e c ( s k , c ∗ ) m'=Dec(sk,c^*) m′=Dec(sk,c∗)
Indistinguishability 安全性(IND):只要求敌手无法区分 c ∗ c^* c∗ 是哪个消息 m 0 , m 1 m_0,m_1 m0,m1 的加密。攻击难度比 OW 更低,这是更强的安全性要求。
PCA & VA & PCVA
现在我们考虑攻击手段,也就是敌手能够访问某些神谕
- 明文检查神谕(Plaintext Checking Oracle):输入密文 c c c 和消息 m m m,检查消息 m m m 是否就是密文 c c c 所加密的,记为 P c o ( m , c ) Pco(m,c) Pco(m,c)
- 密文有效性神谕(Ciphertext Validity Oracle):输入密文 c c c,检查密文 c c c 是否会输出 ⊥ \perp ⊥,记为 C v o ( c ) Cvo(c) Cvo(c)
当然,需要约束下神谕的能力:
- 明文检查神谕只能回答 m ∈ M m \in M m∈M 的那些请求,对于请求 ( m ∉ M , c ) (m\notin M,c) (m∈/M,c) 应当回复 ⊥ \perp ⊥ 而非 0 / 1 0/1 0/1,否则 P c o ( ⊥ , c ) Pco(\perp,c) Pco(⊥,c) 就完全模拟了 C v o ( c ) Cvo(c) Cvo(c)
- 密文有效性神谕对于请求 c = c ∗ c=c^* c=c∗ 应当回复 ⊥ \perp ⊥ 而非 0 / 1 0/1 0/1,否则 C v o ( c ∗ ) Cvo(c^*) Cvo(c∗) 就可以用于区分 c ∗ c^* c∗ 是随机生成的(如果它是非法密文)还是正确加密的(必然是有效密文)
现在我们定义 PKE 的 OW-ATK 安全性,其中的 ATK 标志着敌手可以访问哪些神谕:

对应的游戏是:

而 IND-CPA PKE 和 IND-CCA KEM 安全性的定义,是很自然的,游戏为:

QROM
量子力学的基本概念:量子比特、量子寄存器、标准正交计算基、叠加态、测量、坍缩。
量子神谕(Quantum Oracles):它是一个映射
∣ x ⟩ ∣ y ⟩ ↦ ∣ x ⟩ ∣ y ⊕ f ( x ) ⟩ |x\rangle|y\rangle \mapsto |x\rangle|y\oplus f(x)\rangle ∣x⟩∣y⟩↦∣x⟩∣y⊕f(x)⟩
其中的 f : { 0 , 1 } n → { 0 , 1 } m f:\{0,1\}^n \to \{0,1\}^m f:{0,1}n→{0,1}m 是待查询的函数, x ∈ { 0 , 1 } n x \in \{0,1\}^n x∈{0,1}n 是经典输入(叠加在寄存器 ∣ x ⟩ |x\rangle ∣x⟩ 中), f ( x ) ∈ { 0 , 1 } m f(x) \in \{0,1\}^m f(x)∈{0,1}m 是经典输出。
量子敌手(Quantum Adversaries):记为 A ∣ f ⟩ A^{|f\rangle} A∣f⟩,它查询 f f f 时利用序列 U ∘ f U \circ f U∘f,其中的 U U U 是酉算子。
Quantum Random Oracle Model:随机神谕是量子访问的(quantum access),而其他的神谕都是经典访问的(classical access),包括 Pco、Cvo、Dec 都是经典的。
有文章指出,不存在量子敌手 A ∣ f ⟩ A^{|f\rangle} A∣f⟩,仅仅量子查询 q q q 次量子神谕 ∣ f ⟩ |f\rangle ∣f⟩,就将它从 2 q 2q 2q-wise independent function 区分出来。因此,量子随机神谕 ∣ G ⟩ |G\rangle ∣G⟩ 可以被视为一个有限域 G F ( 2 m ) GF(2^m) GF(2m) 上度数为 2 q H 2q_H 2qH 的随机多项式,将查询 QRO 视为对这个随机多项式的求值。
QROM 下的解密失败率的定义为
Pr [ C O R - Q R O P K E A → 1 ] ≤ δ ( q G ) \Pr[COR\text-QRO_{PKE}^A \to 1] \le \delta(q_G) Pr[COR-QROPKEA→1]≤δ(qG)
对应的游戏是

Fine-Grained FO
[HHK17] 给出了细粒度的变换,先从 OW-CPA 构造出 IND-CPA 或者 OW-PCA,然后再继续构造出 IND-CCA,他们的归约比之前的工作更紧。

将这些细粒度转换相互组合,可以获得多种 FO-like 变换:

它的归约算法中考虑了解密失败率的影响,并且 ROM 下的归约过程比之前的工作更紧。不过 QROM 下的归约是十分不紧的,这是个 Open Problem。
T 变换
采取了去随机化(Derandomization)和重加密(Re-encryption)的结构,
- 它将任意的 OW-CPA PKE 转化为 OW-PCA det.PKE
- 如果底层 PKE 额外满足 IND-CPA,那么 ROM 归约是紧的
- 如果底层 PKE 额外满足 γ \gamma γ-spraed,那么得到的 det.PKE 也是 OW-VA 的
Encrypt-with-Hash construction:给定底层加密方案 P K E PKE PKE 和哈希函数 G G G,输出的 P K E 1 = T [ P K E , G ] PKE_1=T[PKE,G] PKE1=T[PKE,G] 是一个确定性的加密方案。
加密:将 G ( m ) G(m) G(m) 作为随机带,
E n c 1 ( p k , m ) : = E n c ( p k , m ; G ( m ) ) Enc_1(pk,m) := Enc(pk,m;G(m)) Enc1(pk,m):=Enc(pk,m;G(m))
解密:先计算 m ′ ← D e c ( s k , c ) m'\gets Dec(sk,c) m′←Dec(sk,c),然后使用重加密检查密文的有效性,
D e c 1 ( s k , c ) : = { m ′ , [ E n c 1 ( p k , m ′ ) = c ] ⊥ , [ E n c 1 ( p k , m ′ ) ≠ c ] Dec_1(sk,c) := \left\{\begin{aligned} m',&& [Enc_1(pk,m') = c]\\ \perp,&& [Enc_1(pk,m') \neq c]\\ \end{aligned}\right. Dec1(sk,c):={m′,⊥,[Enc1(pk,m′)=c][Enc1(pk,m′)=c]
在 ROM 下,从 OW-CPA 转换到 OW-PCA 的归约是不紧的,

在 ROM 下,从 IND-CPA 转换到 OW-PCA 的归约是紧的,

在 QROM 下,变换 T 也是安全的,不过归约是不紧的,

U 变换
[HHK17] 根据隐式/显式拒绝,以及产生共享秘钥的计算方式,给出了四种变换,
- 它们将 OW-PCA PKE 转化为 IND-CCA KEM
- 如果 PKE 额外是确定性的,那么就只需它是 OW-CPA 的
一、采取 K = H ( c , m ) K=H(c,m) K=H(c,m) 的转换方案(底层 PKE 任意),封装算法:随机采样 m ← M m \gets M m←M,
E n c a p s ( p k ) : = ( c ← E n c ( p k , m ; r ) , K : = H ( c , m ) ) Encaps(pk) := (c \gets Enc(pk,m;r), K:=H(c,m)) Encaps(pk):=(c←Enc(pk,m;r),K:=H(c,m))
解封装:先计算 m ′ ← D e c ( s k , c ) m' \gets Dec(sk,c) m′←Dec(sk,c),然后检查是否拒绝,
-
隐式拒绝(implicit rejection)
D e c a p s ⊥̸ ( s k , c ) : = { H ( c , m ′ ) , [ m ′ ≠ ⊥ ] H ( c , s ) , [ m ′ = ⊥ ] Decaps^{\not\perp}(sk,c) := \left\{\begin{aligned} H(c,m'),&& [m' \neq \perp]\\ H(c,s),&& [m' = \perp]\\ \end{aligned}\right. Decaps⊥(sk,c):={H(c,m′),H(c,s),[m′=⊥][m′=⊥]
其中的 s ∈ { 0 , 1 } n s \in \{0,1\}^n s∈{0,1}n 是随机种子,作为 s k sk sk 的一部分 -
显式拒绝(explicit rejection)
D e c a p s ⊥ ( s k , c ) : = { H ( c , m ′ ) , [ m ′ ≠ ⊥ ] ⊥ , [ m ′ = ⊥ ] Decaps^{\perp}(sk,c) := \left\{\begin{aligned} H(c,m'),&& [m' \neq \perp]\\ \perp,&& [m' = \perp]\\ \end{aligned}\right. Decaps⊥(sk,c):={H(c,m′),⊥,[m′=⊥][m′=⊥]
这其实就是 KEM 版本的 REACT/GEM 变换,见 [Dent03]
二、采取 K = H ( m ) K=H(m) K=H(m) 的转换方案(它要求 PKE 是确定性的,比如 T 变换的结果),封装算法:随机采样 m ← M m \gets M m←M,
E n c a p s m ( p k ) : = ( c ← d e t . E n c ( p k , m ) , K : = H ( m ) ) Encaps_m(pk) := (c \gets det.Enc(pk,m), K:=H(m)) Encapsm(pk):=(c←det.Enc(pk,m),K:=H(m))
解封装:先计算 m ′ ← D e c ( s k , c ) m' \gets Dec(sk,c) m′←Dec(sk,c),然后检查是否拒绝,
-
隐式拒绝(implicit rejection)
D e c a p s m ⊥̸ ( s k , c ) : = { H ( m ′ ) , [ m ′ ≠ ⊥ ] H ( c , s ) , [ m ′ = ⊥ ] Decaps^{\not\perp}_m(sk,c) := \left\{\begin{aligned} H(m'),&& [m' \neq \perp]\\ H(c,s),&& [m' = \perp]\\ \end{aligned}\right. Decapsm⊥(sk,c):={H(m′),H(c,s),[m′=⊥][m′=⊥]
其中的 s ∈ { 0 , 1 } n s \in \{0,1\}^n s∈{0,1}n 是随机种子,作为 s k sk sk 的一部分 -
显式拒绝(explicit rejection)
D e c a p s m ⊥ ( s k , c ) : = { H ( m ′ ) , [ m ′ ≠ ⊥ ] ⊥ , [ m ′ = ⊥ ] Decaps^{\perp}_m(sk,c) := \left\{\begin{aligned} H(m'),&& [m' \neq \perp]\\ \perp,&& [m' = \perp]\\ \end{aligned}\right. Decapsm⊥(sk,c):={H(m′),⊥,[m′=⊥][m′=⊥]
这其实就是 KEM 版本的原始 FO 变换,见 [Dent03]
在 ROM 下,变换 U ⊥ U^{\perp} U⊥ 的归约是紧的,

在 ROM 下,变换 U ⊥̸ U^{\not\perp} U⊥ 的归约是紧的,

在 ROM 下,变换 U m ⊥ U_m^{\perp} Um⊥ 的归约是紧的,需要 PKE 是 det 的

在 ROM 下,变换 U m ⊥̸ U_m^{\not\perp} Um⊥ 的归约是紧的,需要 PKE 是 det 的

在 QROM 下 U 变换不工作。
FO-like KEM
现在,我们组合 T 变换、U 变换,可以得到四种 FO 变换:

在 ROM 下,综合 T 变换以及 U 变换的归约结果,给出 IND-CCA 敌手的最终优势,以及相关参数的选取建议:

QU 变换
可以证明 T 变换在 QROM 下依然工作,但是上述的四种 U 变换并不行。略微修改 U m ⊥ U_m^\perp Um⊥,就可以获得量子下安全的转换方案。
封装算法:随机采样 m ← M m \gets M m←M,密文中额外添加 m m m 的摘要 d d d,要求 H ′ , H H',H H′,H 是独立的 QRO,
Q E n c a p s m ( p k ) : = ( c t : = ( c ← E n c ( p k , m ) , d : = H ′ ( m ) ) , K : = H ( m ) ) QEncaps_m(pk) := (ct:=(c \gets Enc(pk,m), d:=H'(m)), K:=H(m)) QEncapsm(pk):=(ct:=(c←Enc(pk,m),d:=H′(m)),K:=H(m))
解封装:
-
显式拒绝:先计算 m ′ ← D e c ( s k , ( c , d ) ) m' \gets Dec(sk,(c,d)) m′←Dec(sk,(c,d)),然后检查是否拒绝,
Q D e c a p s m ⊥ ( s k , c ) : = { H ( m ′ ) , [ m ′ ≠ ⊥ ] ∧ [ H ′ ( m ′ ) = d ] ⊥ , [ m ′ = ⊥ ] ∨ [ H ′ ( m ′ ) ≠ d ] QDecaps^{\perp}_m(sk,c) := \left\{\begin{aligned} H(m'),&& [m' \neq \perp] \wedge [H'(m')=d]\\ \perp,&& [m' = \perp] \vee [H'(m')\neq d]\\ \end{aligned}\right. QDecapsm⊥(sk,c):={H(m′),⊥,[m′=⊥]∧[H′(m′)=d][m′=⊥]∨[H′(m′)=d] -
隐式拒绝:先计算 m ′ ← D e c ( s k , ( c , d ) ) m' \gets Dec(sk,(c,d)) m′←Dec(sk,(c,d)),然后检查是否拒绝,
Q D e c a p s m ⊥̸ ( s k , c ) : = { H ( m ′ ) , [ m ′ ≠ ⊥ ] ∧ [ H ′ ( m ′ ) = d ] H ( ( c , d ) , s ) , [ m ′ = ⊥ ] ∨ [ H ′ ( m ′ ) ≠ d ] QDecaps^{\not\perp}_m(sk,c) := \left\{\begin{aligned} H(m'),&& [m' \neq \perp] \wedge [H'(m')=d]\\ H((c,d),s),&& [m' = \perp] \vee [H'(m')\neq d]\\ \end{aligned}\right. QDecapsm⊥(sk,c):={H(m′),H((c,d),s),[m′=⊥]∧[H′(m′)=d][m′=⊥]∨[H′(m′)=d]
在 QROM 下,变换 Q U m ⊥ QU_m^{\perp} QUm⊥ 的归约是不紧的,注意这里不再需要 PKE 是 det 的,

在 QROM 下,变换 Q U m ⊥̸ QU_m^{\not\perp} QUm⊥ 的归约是不紧的,注意这里也不需要 PKE 是 det 的,

另外,在 ROM 下两者都是紧的。
Quantum KEM
现在,我们组合 T 变换、QU 变换,可以得到两种 QFO 变换:

上述的 G , H , H ′ G, H, H' G,H,H′ 的输入都是同一个 m m m,因此实例化的时候可以使用一个输出足够长的 Hash 函数(NTTRU 的思路),统一地计算出随机摘要,然后切分成 3 块来分别使用。
S 变换
因为 T 变换从 OW-CPA 到 IND-CPA 是不紧的,[HHK17] 给出了一种 trade-off between efficiency and tightness.,利用多个独立的 PKE 密文,使得归约时嵌入 OW-CPA 挑战时更加容易,猜测次数变少,从而减小了损失因子。
加密:随机采样 x 1 , ⋯ , x l x_1,\cdots,x_l x1,⋯,xl,以及随机带 r 1 , ⋯ , r l r_1,\cdots,r_l r1,⋯,rl,
E n c l ( p k , m ) : = ( m ⊕ F ( x 1 , ⋯ , x l ) , E n c ( p k , x 1 ; r 1 ) , ⋯ , E n c ( p k , x l ; r l ) ) Enc_l(pk,m) := (m\oplus F(x_1,\cdots,x_l),Enc(pk,x_1;r_1),\cdots,Enc(pk,x_l;r_l)) Encl(pk,m):=(m⊕F(x1,⋯,xl),Enc(pk,x1;r1),⋯,Enc(pk,xl;rl))
解密:计算 x i ′ ← D e c ( s k , c i ) , ∀ i = 1 , ⋯ , l x_i' \gets Dec(sk,c_i),\forall i=1,\cdots,l xi′←Dec(sk,ci),∀i=1,⋯,l,
D e c l ( s k , ( c 0 , c 1 , ⋯ , c l ) ) = c 0 ⊕ F ( x 1 ′ , ⋯ , x l ′ ) Dec_l(sk,(c_0,c_1,\cdots,c_l)) = c_0 \oplus F(x_1',\cdots,x_l') Decl(sk,(c0,c1,⋯,cl))=c0⊕F(x1′,⋯,xl′)
在 ROM 下,从 OW-CPA 到 IND-CPA 是紧的,代价是计算效率增加、解密失败率增加,

它在 QROM 下不工作。
Reduce RLWE to IND-CCA
[AOP+17] 使用底层 RLWE-based PKE 特有的弱同态性质,在 ROM 下直接将 RLWE 归约到了 IND-CCA KEM,并不存在中间的 IND-CPA PKE,获得了紧的归约。它不是通用的转换,仅仅适用于格密码,他们称之为 LIMA(LattIce MAthematics)。对比 [Dent03] 的通用结果是不紧的。
此外,LIMA 的 IND-CCA KEM 相较于 IND-CPA PKE 并没有 ciphertext overhead,两者的通信开销是完全一样的。
首先,构造 IND-CPA 安全的 RLWE-based PKE,


然后,简单地根据 [Dent03] 的现代化 FO-KEM 描述,将它转化为 IND-CCA KEM,

不过,如果直接应用 [Dent03] 的通用归约结果(从 OW-CPA 到 IND-CCA),它是不紧的。[HHK17] 已经证明了 [Dent03] 的通用构造对于 IND-CPA 是紧的。而恰好上述的 RLWE-based PKE 是紧归约到 RLWE 问题的,因此 [AOP+17] 完全可以视为 [HHK17] 的一个特例。
针对于 LWE 的特殊性,[AOP+17] 给出了一个不通用的紧归约,

其中的 A d v L W E Adv^{LWE} AdvLWE 游戏是:

相关文章:

FO-like Transformation
参考文献: [RS91] Rackoff C, Simon D R. Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack[C]//Annual international cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991: 433-444.[BR93] Bellare M…...
通过ros系统中websocket中发送sensor_msgs::Image数据给web端显示(三)
通过ros系统中websocket中发送sensor_msgs::Image数据给web端显示(三) 不使用base64编码方式传递 #include <ros/ros.h> #include <signal.h> #include <sensor_msgs/Image.h> #include <message_filters/subscriber.h> #include <message_filter…...
Navicat 技术指引 | 适用于 GaussDB 的模型功能
Navicat Premium(16.2.8 Windows版或以上) 已支持对 GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...
Ubuntu18.4中安装wkhtmltopdf + Odoo16配置【二】
deepin Linux 安装wkhtmltopdf 1、先从官网的链接里下载linux对应的包 wkhtmltopdf/wkhtmltopdf 下载需要的版本,推荐版本,新测有效: wkhtmltox-0.12.4_linux-generic-amd64.tar.xz 2、解压下载的文件 解压后会有一个wkhtmltox文件夹 3…...

RC-MVSNet:无监督的多视角立体视觉与神经渲染--论文笔记(2022年)
RC-MVSNet:无监督的多视角立体视觉与神经渲染--论文笔记(2022年) 摘要1 引言2 相关工作2.1 基于监督的MVS2.2 无监督和自监督MVS2.3 多视图神经渲染 3 实现方法3.1 无监督的MVS网络 Chang, D. et al. (2022). RC-MVSNet: Unsupervised Multi-…...

gradle构建项目速度优化及排查方式
文章目录 一、前言二、Android项目优化1、相关配置2、构建速度分析 三、Gradle项目通用优化1、分析构建耗时2、使用配置进行优化3、优化依赖解析a. 避免不必要和未使用的依赖项b. 优化存储库顺序 c. 最小化动态和快照版本d. 通过构建扫描查找动态和变化的版本e. 通过构建扫描可…...
MSI Center,XBox从任务栏取消固定
1,设置查看方式中隐藏项目可见 2,进入文件夹:C:\Users\Default\AppData\Local\Microsoft\Windows\Shell 找到下面这两个文件夹: 3,修改文件名或者删除这两个文件即可...
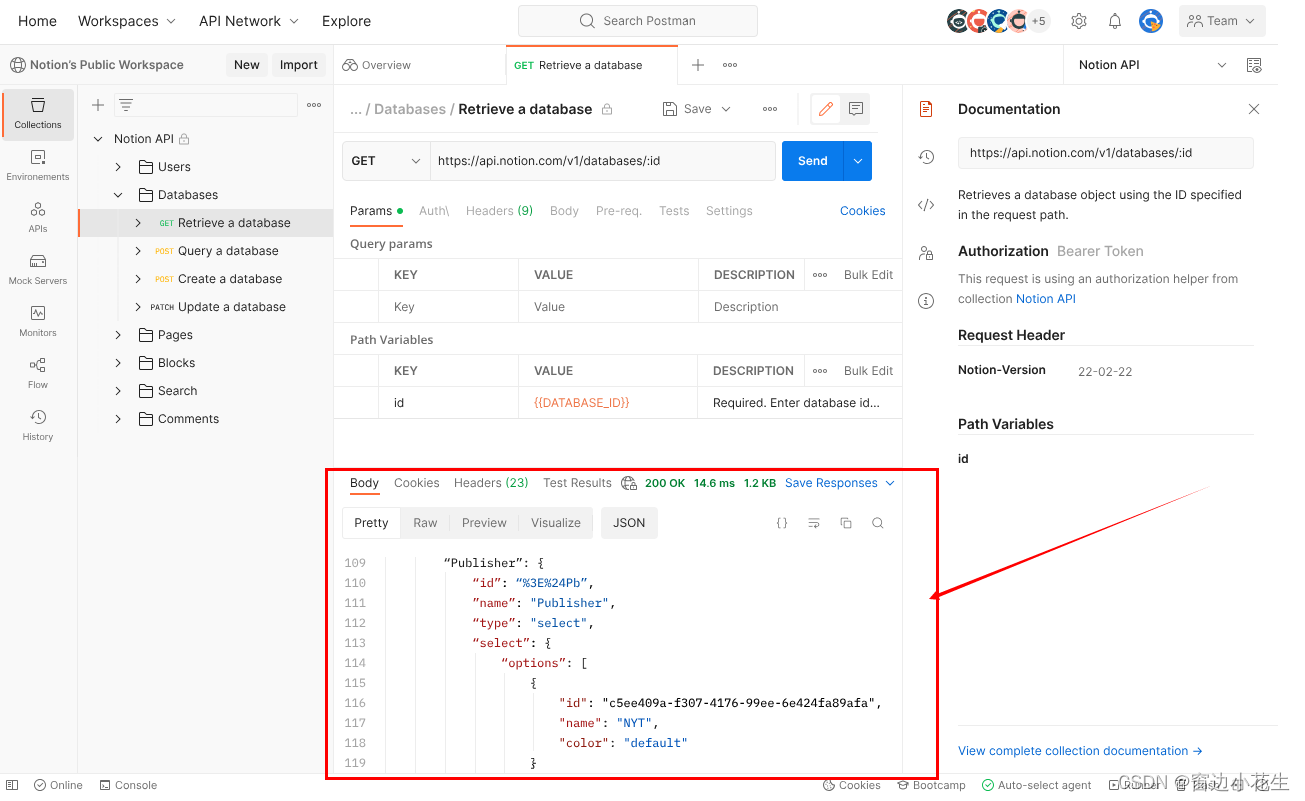
1、postman的安装及使用
一、安装、登录 1.安装 下载地址 2.注册登录(保存云服务进度) 二、界面介绍 三、执行接口测试页面 请求页签: 1、params:当是get请求时,通过params传参 2、authorization:鉴权 3、headers࿱…...

VUE简易计划清单
目录 效果预览图 完整代码 效果预览图 完整代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>…...

c++日志单例实现
为了使项目的所有日志都打印到同一个日志中,必须使得所有类使用同一个日志,因此将日志类实现为单例。 .h文件 #pragma once#include<fstream>class LogHablee { private:LogHablee(std::string& dbg_dir);LogHablee(const LogHablee&) …...
,返回其最大和 某知名企业笔试题)
C/C++实现:找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和 某知名企业笔试题
目录 题目描述: 示例 1: 示例 2: 示例 3: 提示: 思路:...

Qt实现绘制自定义形状
先创建一个继承自QWidget的控件: class MyPainterWidget:public QWidget 重写各种鼠标方法: protected:void paintEvent(QPaintEvent *) override;void mousePressEvent(QMouseEvent *e) override; //按下void mouseMoveEvent(QMouseEvent *e) …...
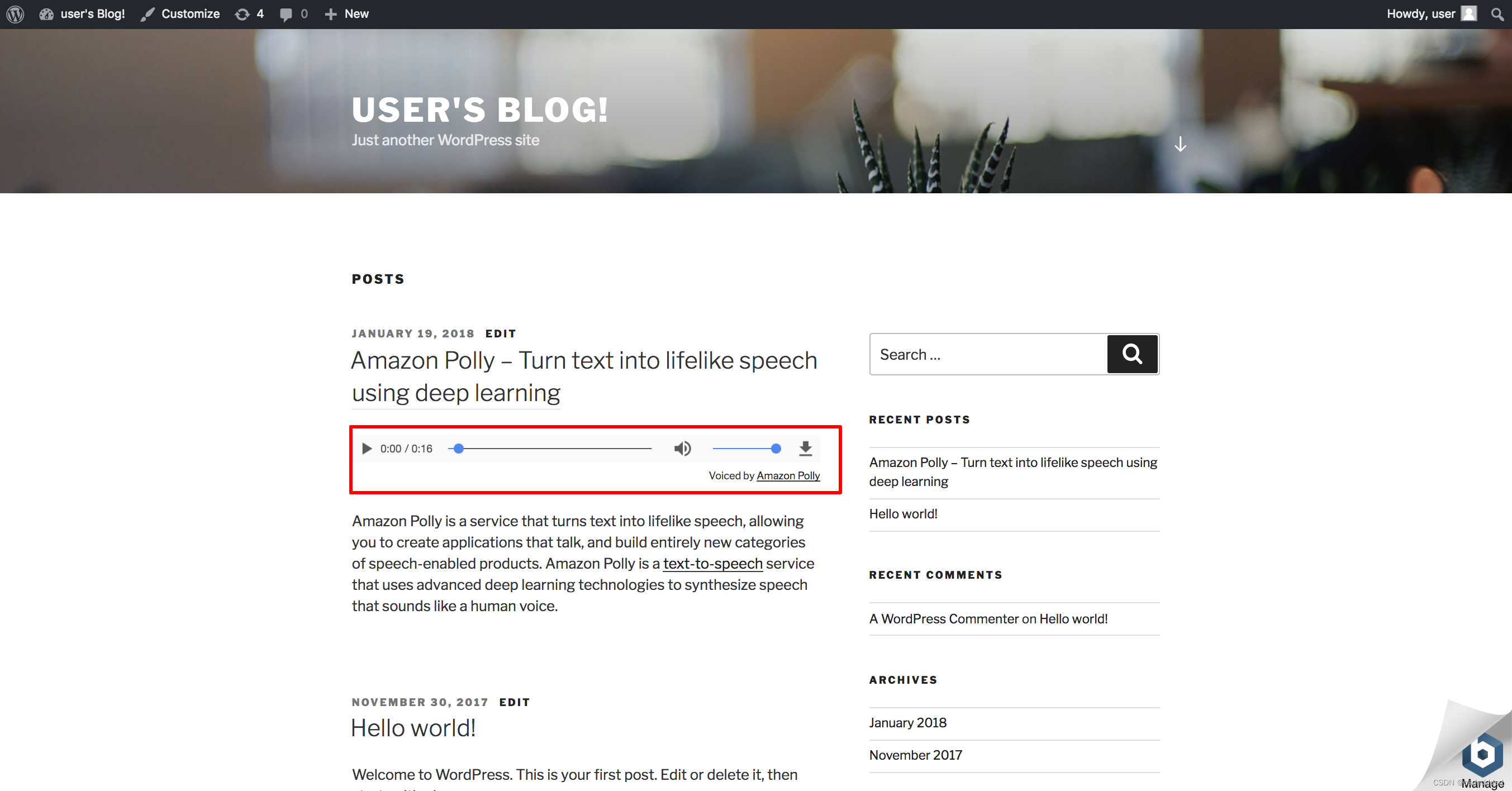
WordPress安装AWS插件实现文本转语音功能
适用于 WordPress 的 AWS 插件示例演示了内容创建者如何轻松地为所有书面内容添加文本转语音功能。随着语音搜索的不断增加,以音频格式提供更多网站内容变得至关重要。通过添加语音功能,网站访客可以通过在线音频播放器和播客应用程序等新渠道使用您的内…...

87-96-多维动态规划、技巧
LeetCode 热题 100 文章目录 LeetCode 热题 100多维动态规划87. 中等-不同路径88. 中等-最小路径和89. 中等-最长回文子串90. 中等-最长公共子序列91. 困难-编辑距离 技巧92. 简单-只出现一次的数字93. 简单-多数元素94. 中等-颜色分类95. 中等-下一个排列96. 中等-寻找重复数 …...

NX二次开发UF_CURVE_ask_wrap_curve_parents 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_ask_wrap_curve_parents Defined in: uf_curve.h int UF_CURVE_ask_wrap_curve_parents(tag_t curve_tag, tag_t * defining_face, tag_t * defining_plane, tag_t * defin…...

使用 HTML、CSS 和 JavaScript 创建图像滑块
使用 HTML、CSS 和 JavaScript 创建轮播图 在本文中,我们将讨论如何使用 HTML、CSS 和 JavaScript 构建轮播图。我们将演示两种不同的创建滑块的方法,一种是基于opacity的滑块,另一种是基于transform的。 创建 HTML 我们首先从 HTML 代码开…...
ubuntu环境删除qtcreator方法
文章目录 方法1方法2方法3参考不同的安装方法,对应不同的删除方法 方法1 apt-get或者dpkg 方法2 QtCreatorUninstaller 方法3 MaintenanceTool...

软件测试基础知识
软件测试基本概念 1、软件程序文档,软件测试程序测试文档测试。 “程序”是指能够实现某种功能的指令的集合,“文档”是指软件在开发、使用和维护过程中产生的图文集合。; 2、软件的分类 按功能分:系统软件、应用软件 按技术架构分…...
 方法生成当前时间的ISO格式字符串,解决UTC时区差问题)
使用 .toISOString() 方法生成当前时间的ISO格式字符串,解决UTC时区差问题
方法分析: 日常开发中,有时我们需要向后端传递的时间值可能并非一个时间对象,而是字符串格式。 例 1:[2023-08-16T08:07:25.577Z] 但是我们通过 new Date() 之后直接使用 .toString() 方法得到的却并非这种格式。 例 2࿱…...
“BMP转PNG一键转换,批量处理图片,迈入高效图片管理新时代“
你是否曾经为了转换图片格式而烦恼?是否曾经因为一张一张地手动转换而感到无奈?现在,我们的全新工具将为你解决这些问题,开启高效图片管理新时代! 首先,我们进入首助编辑高手主页面,会看到有多种…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
