基于C#实现线段树
一、线段树
线段树又称"区间树”,在每个节点上保存一个区间,当然区间的划分采用折半的思想,叶子节点只保存一个值,也叫单元节点,所以最终的构造就是一个平衡的二叉树,拥有 CURD 的 O(lgN)的时间。
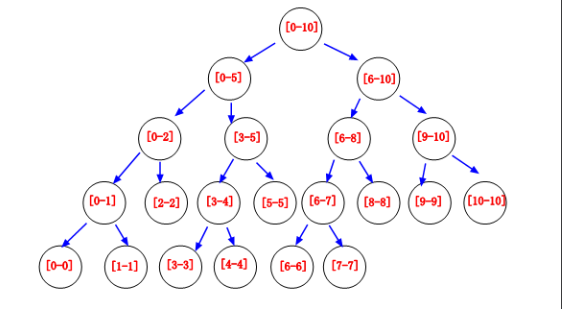
从图中我们可以清楚的看到[0-10]被划分成线段的在树中的分布情况,针对区间[0-N],最多有 2N 个节点,由于是平衡二叉树的形式也可以像堆那样用数组来玩,不过更加耗费空间,为最多 4N 个节点,在针对 RMQ 的问题上,我们常常在每个节点上增加一些 sum,max,min 等变量来记录求得的累加值,当然你可以理解成动态规划的思想,由于拥有 logN 的时间,所以在 RMQ 问题上比数组更加优美。
二、代码
1、在节点中定义一些附加值,方便我们处理 RMQ 问题。
#region 线段树的节点/// <summary>/// 线段树的节点/// </summary>public class Node{/// <summary>/// 区间左端点/// </summary>public int left;/// <summary>/// 区间右端点/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 节点的sum值/// </summary>public int Sum;/// <summary>/// 节点的Min值/// </summary>public int Min;/// <summary>/// 节点的Max值/// </summary>public int Max;}#endregion
2、构建(Build)
前面我也说了,构建有两种方法,数组的形式或者链的形式,各有特点,我就采用后者,时间为 O(N)。
#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//说明已经到根了,当前当前节点的max,sum,min值(回溯时统计上一层节点区间的值)if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//统计左右子树的值(min,max,sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion
3、区间查询
在线段树中,区间查询还是有点小麻烦的,存在三种情况。
① 完全包含:也就是节点的线段范围完全在查询区间的范围内,这说明我们要么到了“单元节点",要么到了一个子区间,这种情况就是我找到了查询区间的某一个子区间,直接累积该区间值就可以了。
② 左交集: 这种情况我们需要到左子树去遍历。
③ 右交集: 这种情况我们需要到右子树去遍历。
比如说:我要查询 Sum[4-8]的值,最终会成为:Sum 总=Sum[4-4]+Sum[5-5]+Sum[6-8],时间为 log(N)。
#region 区间查询/// <summary>/// 区间查询(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 区间查询/// </summary>/// <param name="left">查询左边界</param>/// <param name="right">查询右边界</param>/// <param name="node">查询的节点</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//说明当前节点完全包含在查询范围内,两点:要么是单元节点,要么是子区间if (left <= node.left && right >= node.right){//获取当前节点的sum值sum += node.Sum;return;}else{//如果当前的left和right 和node的left和right无交集,此时可返回if (node.left > right || node.right < left)return;//找到中间线var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion
4、更新操作
这个操作跟树状数组中的更新操作一样,当递归的找到待修改的节点后,改完其值然后在当前节点一路回溯,并且在回溯的过程中一路修改父节点的附加值直到根节点,至此我们的操作就完成了,复杂度同样为 logN。
#region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中间值var middle = (node.left + node.right) / 2;//遍历左子树if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍历右子树if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改,复杂度为lgNif (index >= node.left && index <= node.right){//说明找到了节点if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯时统计左右子树的值(min,max,sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion
最后我们做个例子,在 2000000 的数组空间中,寻找 200-3000 区间段的 sum 值,看看他的表现如何。
using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;namespace ConsoleApplication2{public class Program{public static void Main(){int[] nums = new int[200 * 10000];for (int i = 0; i < 10000 * 200; i++){nums[i] = i;}Tree tree = new Tree();//将当前数组构建成 “线段树”tree.Build(nums);var watch = Stopwatch.StartNew();var sum = tree.Query(200, 3000);watch.Stop();Console.WriteLine("耗费时间:{0}ms, 当前数组有:{1}个数字, 求出Sum=:{2}", watch.ElapsedMilliseconds, nums.Length, sum);Console.Read();}}public class Tree{#region 线段树的节点/// <summary>/// 线段树的节点/// </summary>public class Node{/// <summary>/// 区间左端点/// </summary>public int left;/// <summary>/// 区间右端点/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 节点的sum值/// </summary>public int Sum;/// <summary>/// 节点的Min值/// </summary>public int Min;/// <summary>/// 节点的Max值/// </summary>public int Max;}#endregionNode nodeTree = new Node();int[] nums;#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//说明已经到根了,当前当前节点的max,sum,min值(回溯时统计上一层节点区间的值)if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//统计左右子树的值(min,max,sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion#region 区间查询/// <summary>/// 区间查询(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 区间查询/// </summary>/// <param name="left">查询左边界</param>/// <param name="right">查询右边界</param>/// <param name="node">查询的节点</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//说明当前节点完全包含在查询范围内,两点:要么是单元节点,要么是子区间if (left <= node.left && right >= node.right){//获取当前节点的sum值sum += node.Sum;return;}else{//如果当前的left和right 和node的left和right无交集,此时可返回if (node.left > right || node.right < left)return;//找到中间线var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion#region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中间值var middle = (node.left + node.right) / 2;//遍历左子树if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍历右子树if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改,复杂度为lgNif (index >= node.left && index <= node.right){//说明找到了节点if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯时统计左右子树的值(min,max,sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion}}

相关文章:

基于C#实现线段树
一、线段树 线段树又称"区间树”,在每个节点上保存一个区间,当然区间的划分采用折半的思想,叶子节点只保存一个值,也叫单元节点,所以最终的构造就是一个平衡的二叉树,拥有 CURD 的 O(lgN)的时间。 从…...

AI智能客服搭建教程附带免费源码
*名称* *版本要求* 服务器 CPU 2核心 ↑运存 4G ↑宽带 5M ↑ 服务器操作系统 Linux Centos7 运行环境 Nginx 1.18 PHP 7.3 MYSQL 5.6 服务器配置及环境要求 PHP设置 一、安装PHP扩展插件:fileinfo、redis、 sg11 二、删除PHP对应版本中的 pcntl_signal 、pcntl_signal_dis…...
四)
Shell脚本:Linux Shell脚本学习指南(第三部分Shell高级)四
十九、Linux Shell trap命令:捕获信号 到目前为止,我们在本教程所见的脚本中还没有需要信号处理功能的,因为它们的内容相对比较简单,执行时间很短,而且不会创建临时文件。而对于较大的或者更复杂的脚本来说࿰…...
牛气霸屏-快抖云推独立版V1.6.7
介绍 快抖云推全插件独立版是最近很火的牛气霸屏系统独立版,牛气霸屏系统就是商家通过系统在线创建抖音或快手霸屏活动,并生成该活动的爆客二维码,用户通过扫二维码即可参加活动(活动可以是领取卡劵,抽奖等࿰…...
ffmpeg下载与配置环境变量
FFmpeg 是一个强大的多媒体框架,可以让用户处理和操纵音频和视频文件。具有易于使用的界面,用户可以在 Windows、Mac 或 Linux Ubuntu 系统上下载 FFmpeg 并将其提取到文件夹中。然后,该软件可以加入 PATH 环境变量中就可以快捷的使用软件了.…...

那些年,关于CKACKS认证的那些事儿?
前言 遥想2020年的年初,疫情封城封村之际,工作之余在B站将尚硅谷的linux中的k8s视频完整系统的学习了一遍,自此像是打通了任督二脉一般,开启了对k8s的探索之旅,一路也是磕磕绊绊的在工作中使用k8s。 终于在23年的6月仲…...
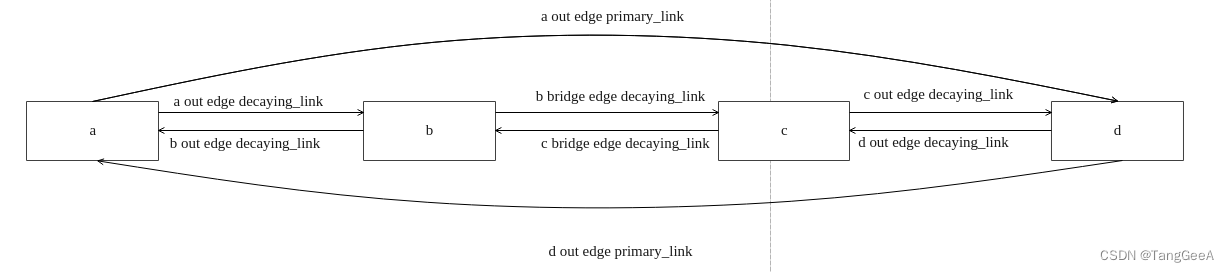
chromium通信系统-mojo系统(一)-ipcz系统代码实现-同Node通信
在chromium通信系统-mojo系统(一)-ipcz系统基本概念一文中我们介绍了ipcz的基本概念。 本章我们来通过代码分析它的实现。 handle系统 为了不对上层api暴露太多细节,实现解耦,也方便于传输,ipcz系统使用handle表示一个对象,hand…...
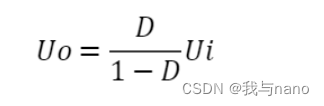
电路 buck-boost相关知识
BUCK-BOOST 文章目录 BUCK-BOOST前言一、DC-DC工作模式电容电感特性伏秒积平衡原理 二、BUCK电路三、BOOST电路四、BUCK-BOOST电路总结 前言 最近需要用到buck-boost相关的电路知识,于是便写下这篇文章复习一下。 一、DC-DC 在学习buck-boost电路之前我们先来看一…...
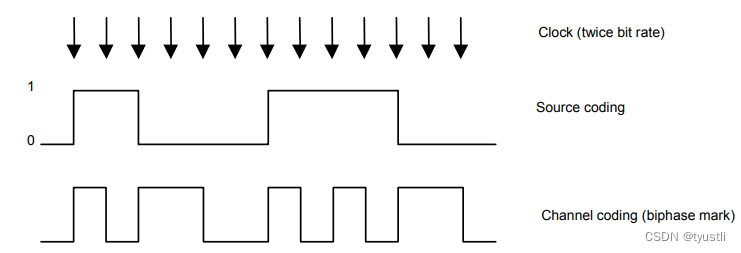
音频——S/PDIF
文章目录 BMC 编码字帧(sub-frame)格式帧(frame)格式参考S/PDIF 是 SONY 和 Philips 公司共同规定的数字信号传输规范,其实就是在 AES/EBU 上进行改动的家用版本。IEC60958 的标准规范囊括了以上两个规范。spdif 采用了双相符号编码(BMC),是将时钟信号和数据信号混合在一起…...

100篇带你入门——嵌入式系统中的程序调试方法
好久不见,最近小猿有点忙,才有时间给大家写文章。今天给大家讲一下在我们单片机开发都用哪些调试工具和调试方法,内容不完善的话,欢迎大家一起交流。 当涉及到嵌入式系统的程序调试时,选择正确的工具和方法是确保系统功…...

【Spring】Spring事务失效问题
📫作者简介:小明java问道之路,2022年度博客之星全国TOP3,专注于后端、中间件、计算机底层、架构设计演进与稳定性建设优化,文章内容兼具广度、深度、大厂技术方案,对待技术喜欢推理加验证,就职于…...
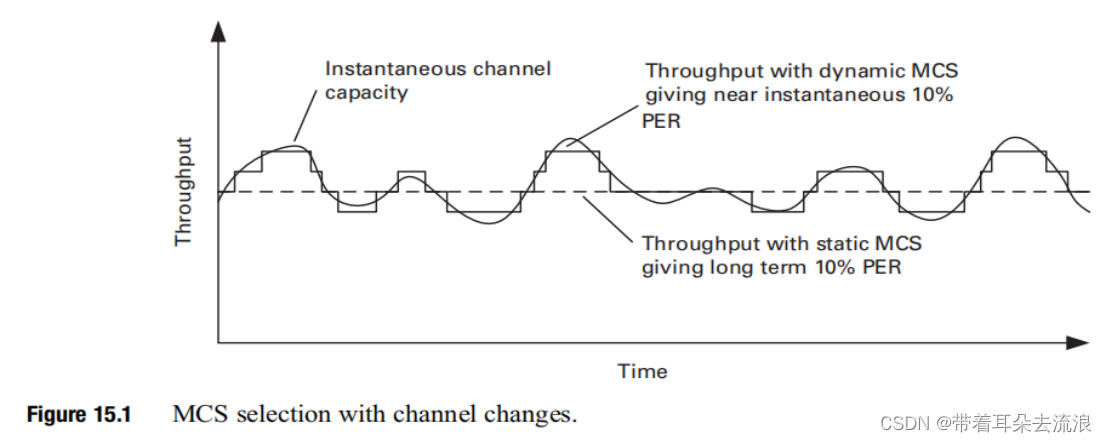
WiFi 发射链路 MCS 自适应机制介绍
链路适配是指发射机选择最优的MCS向特定的接收机发送数据的过程。链路自适应算法的实现有其特殊性,但通常基于测量的数据包错误率(PER)。大多数算法监视PER并调整MCS以跟踪一个最佳的长期平均值,以平衡由于使用更高MCS发送更短数据包而减少的开销和由于更…...

【Linux常用命令】-文件写入相关
一、rm命令,文件删除 1.相关参数 -f(–force):强制删除文件或目录,无需确认。 -r(–recursive):递归地删除目录及其内容。 -i(–interactive):交…...
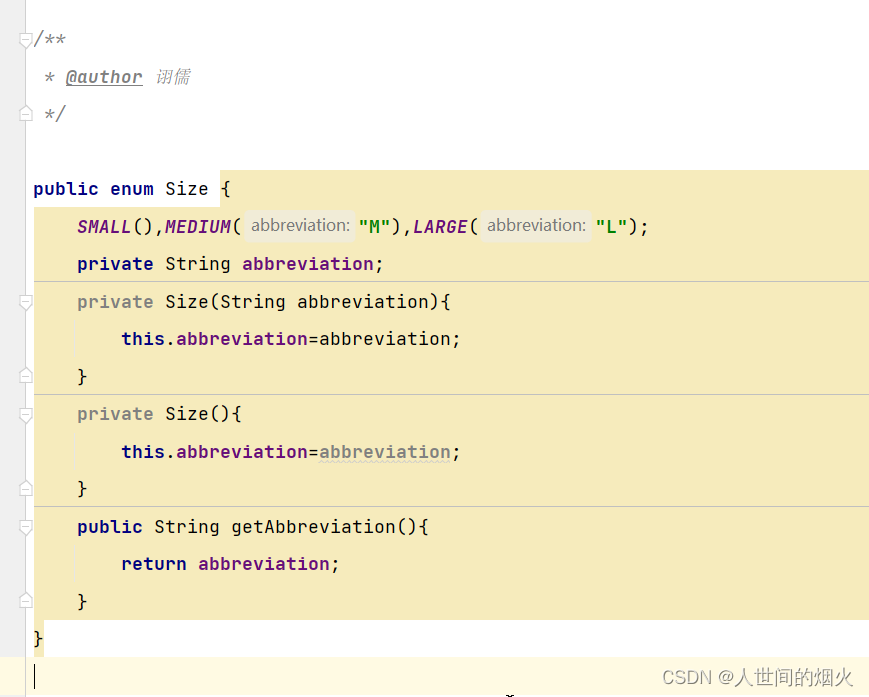
枚举的第一行
2023年11月26日 问题: 好奇enum的所声明的枚举类的第一行是什么 从java技术卷1中第五章5.6中,了解是枚举类的实例 验证 错误信息: 解释: 此时只有有参构造 在这个枚举类里不能使用空,大概意思是说不能使用空参创建实例 校验 在原有的基础上创建一个无参构造 结果:不再报错,第…...
)
LeetCode.707设计链表(链表相关操作一篇就够了)
LeetCode.707设计链表 1.问题描述2.解题思路3.代码 1.问题描述 你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双…...
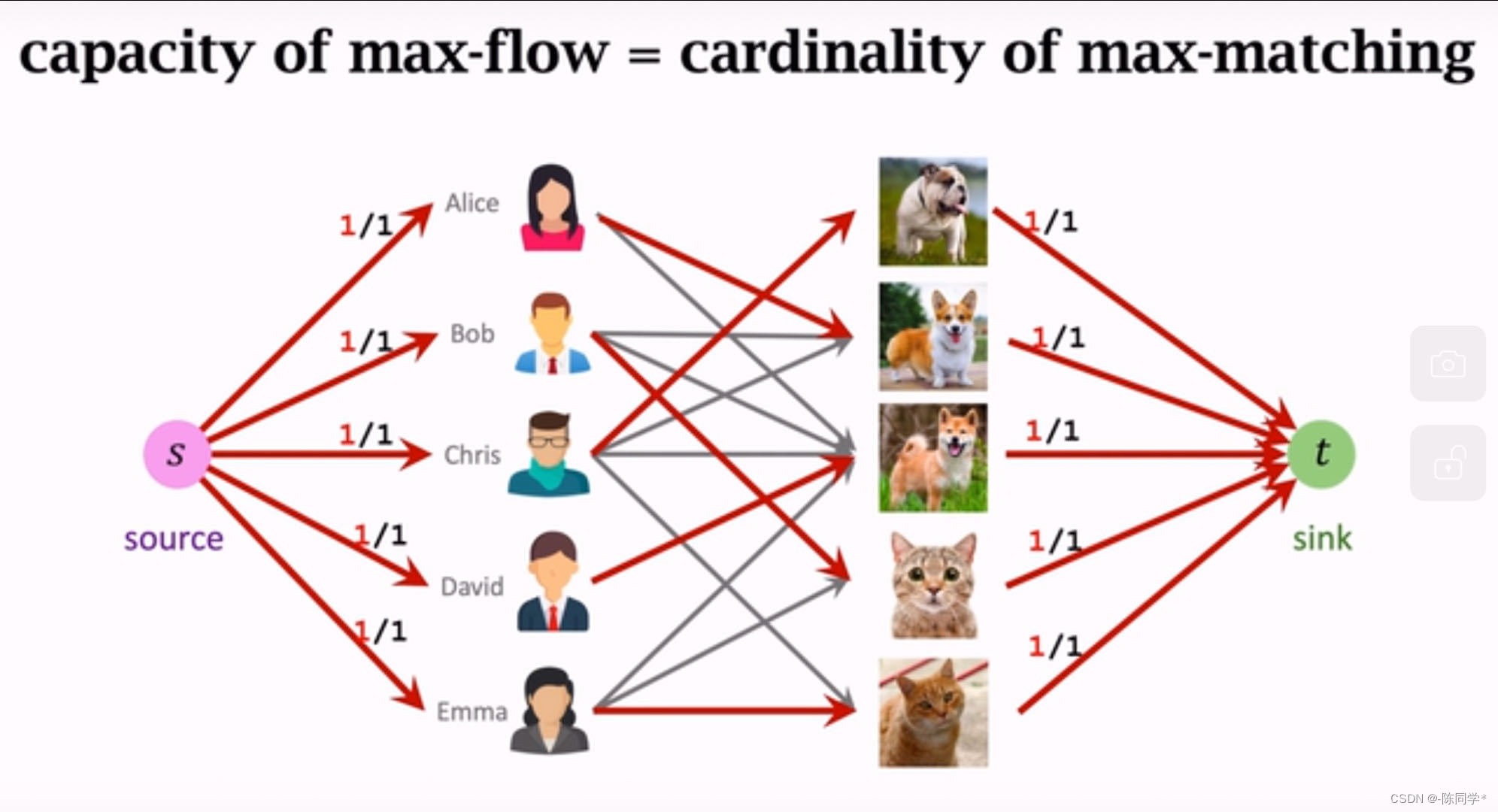
图论——二部图及其算法
什么是二部图 二部图的判定 例子1 任选一个节点染成红色 红色的邻居染成蓝色 蓝色邻居染成红色 例子2 这个不是二部图 无权二部图的最大匹配...

实现简单的操作服务器和客户端(下)
一、说明 描述:本教程介绍如何使用 simple_action_client 库创建斐波那契操作客户端。此示例程序创建一个操作客户端并将目标发送到操作服务器。 内容 代码代码解释编译运行操作客户端连接服务器和客户端...

第二十章 解读PASCAL VOC2012与MS COCO数据集(工具)
PASCAL VOC2012数据集 Pascal VOC2012官网地址:http://host.robots.ox.ac.uk/pascal/VOC/voc2012/ 官方发表关于介绍数据集的文章 《The PASCALVisual Object Classes Challenge: A Retrospective》:http://host.robots.ox.ac.uk/pascal/VOC/pubs/everi…...

FreeRTOS列表和列表项
目录 列表和列表项 关于列表的一些操作 初始化列表 初始化列表项 列表插入列表项 列表项末尾插入 重点 pxIndex指向的是什么 xItemValue存的是什么 vListInsertEnd()的插入位置 List的头尾在哪里? 通用链表的三种实现方式 方法一 方法二 方法三 总结 Fre…...

【go语言实现一个webSocket的一个demo】
go语言实现一个webSocket的一个demo 前端代码 <html lang"zh-CN"><head></head><body> <script type"text/javascript">// header(Access-Control-Allow-Origin:*);var sock null;var wsuri "ws://127.0.0.1:9999&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
