【JavaEE】多线程 (2) --线程安全
目录
1. 观察线程不安全
2. 线程安全的概念
3. 线程不安全的原因
4. 解决之前的线程不安全问题
5. synchronized 关键字 - 监视器锁 monitor lock
5.1 synchronized 的特性
5.2 synchronized 使⽤⽰例
1. 观察线程不安全
package thread;
public class ThreadDemo19 {private static int count = 0;public static void main(String[] args) throws InterruptedException {//创建两个线程,每个线程都针对上面的count变量循环自增5w次Thread t1 = new Thread(()-> {for(int i = 0; i<50000; i++) {count++;}});Thread t2 = new Thread(()-> {for(int i = 0; i<50000; i++) {count++;}});t1.start();t2.start();t1.join();t2.join();System.out.println(count);}
}执行上面的代码,我们发现结果并不是100000, 并且多次运行, 每次的结果都有所不同:
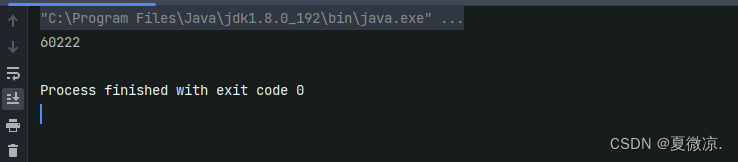
这就是线程不安全的一个例子.
2. 线程安全的概念
想给出⼀个线程安全的确切定义是复杂的,但我们可以这样认为:
如果多线程环境下代码运⾏的结果是符合我们预期的,即在单线程环境应该的结果,则说这个程序是线程安全的。
3. 线程不安全的原因
线程调度是随机的
- 这是线程安全问题的罪魁祸⾸
- 随机调度使⼀个程序在多线程环境下, 执⾏顺序存在很多的变数.
- 程序猿必须保证在任意执⾏顺序下 , 代码都能正常⼯作.
修改共享数据
多个线程修改同⼀个变量
上⾯的线程不安全的代码中, 涉及到多个线程针对 count 变量进⾏修改. 此时这个 count 是⼀个多个线程都能访问到的 "共享数据"
原⼦性
什么是原⼦性
我们把⼀段代码想象成⼀个房间,每个线程就是要进⼊这个房间的⼈。如果没有任何机制保证,A进⼊ 房间之后,还没有出来;B 是不是也可以进⼊房间,打断 A 在房间⾥的隐私。这个就是不具备原⼦性的。
那我们应该如何解决这个问题呢?是不是只要给房间加⼀把锁,A 进去就把⻔锁上,其他⼈是不是就进不来了。这样就保证了这段代码的原⼦性了。 有时也把这个现象叫做同步互斥,表⽰操作是互相排斥的。
⼀条 java 语句不⼀定是原⼦的,也不⼀定只是⼀条指令
⽐如刚才我们看到的 count++,其实是由三步操作组成的:
1. 从内存把数据读到 CPU
2. 进⾏数据更新
3. 把数据写回到 CPU
不保证原⼦性会给多线程带来什么问题
如果⼀个线程正在对⼀个变量操作,中途其他线程插⼊进来了,如果这个操作被打断了,结果就可能是错误的。
这点也和线程的抢占式调度密切相关. 如果线程不是 "抢占" 的, 就算没有原⼦性, 也问题不⼤.
可⻅性
可⻅性指, ⼀个线程对共享变量值的修改,能够及时地被其他线程看到
4. 解决之前的线程不安全问题
使用 synchronized 关键字将一条指令的多个操作, 打包成一个原子的操作.

下面是使用 synchronized 来解决上面代码的问题:


如果两个线程, 针对不同的对象加锁, 也会存在线程安全问题.
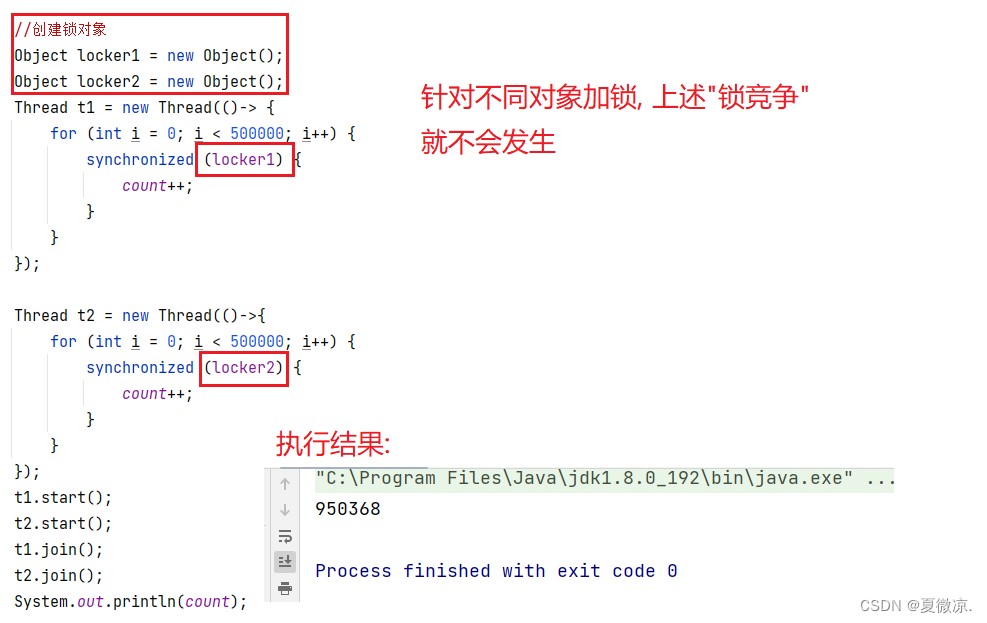
如果一个线程加锁, 一个线程不加锁, 是否会存在线程安全问题?
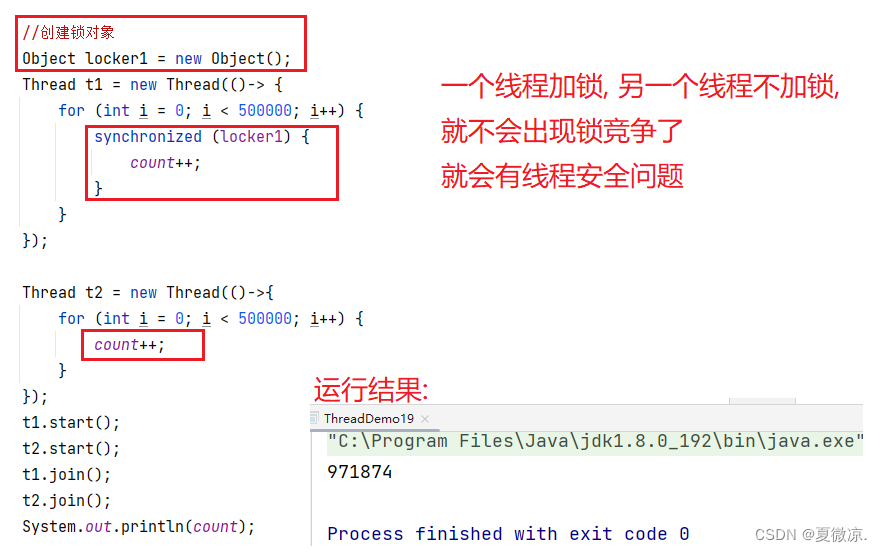
针对加锁操作的一些混淆理解
把count 放到一个Test t对象中, 通过类方法add 来进行修改, 加锁的时候锁对象写作 this
package thread;
class Test {public int count = 0;public void add() {synchronized (this) {count++;}}
}
public class ThreadDemo20 {public static void main(String[] args) throws InterruptedException {Test t = new Test();Thread t1 = new Thread(()->{for (int i = 0; i < 50000; i++) {t.add();}});Thread t2 = new Thread(()->{for (int i = 0; i < 50000; i++) {t.add();}});t1.start();t2.start();t1.join();t2.join();System.out.println("count = " + t.count);}
}也可以使用类对象:


5. synchronized 关键字 - 监视器锁 monitor lock
5.1 synchronized 的特性
1) 互斥
synchronized 会起到互斥效果, 某个线程执⾏到某个对象的 synchronized 中时, 其他线程如果也执⾏ 到同⼀个对象 synchronized 就会阻塞等待
- 进⼊ synchronized 修饰的代码块, 相当于 加锁
- 退出 synchronized 修饰的代码块, 相当于 解锁

synchronized⽤的锁是存在Java对象头⾥的。
可以粗略理解成, 每个对象在内存中存储的时候, 都存有⼀块内存表⽰当前的 "锁定" 状态(类似于厕所 的 "有⼈/⽆⼈").
如果当前是 "⽆⼈" 状态, 那么就可以使⽤, 使⽤时需要设为 "有⼈" 状态.
如果当前是 "有⼈" 状态, 那么其他⼈⽆法使⽤, 只能排队
理解 "阻塞等待".
针对每⼀把锁, 操作系统内部都维护了⼀个等待队列. 当这个锁被某个线程占有的时候, 其他线程尝试 进⾏加锁, 就加不上了, 就会阻塞等待, ⼀直等到之前的线程解锁之后, 由操作系统唤醒⼀个新的线程, 再来获取到这个锁.
注意:
- 上⼀个线程解锁之后, 下⼀个线程并不是⽴即就能获取到锁. ⽽是要靠操作系统来 "唤醒". 这也就 是操作系统线程调度的⼀部分⼯作.
- 假设有 A B C 三个线程, 线程 A 先获取到锁, 然后 B 尝试获取锁, 然后 C 再尝试获取锁, 此时 B 和 C 都在阻塞队列中排队等待. 但是当 A 释放锁之后, 虽然 B ⽐ C 先来的, 但是 B 不⼀定就能获取到锁, ⽽是和 C 重新竞争, 并不遵守先来后到的规则.
2) 可重⼊
synchronized 同步块对同⼀条线程来说是可重⼊的,不会出现⾃⼰把⾃⼰锁死的问题;
理解 "把⾃⼰锁死"
⼀个线程没有释放锁, 然后⼜尝试再次加锁.
// 第⼀次加锁, 加锁成功
lock();
// 第⼆次加锁, 锁已经被占⽤, 阻塞等待.
lock();
按照之前对于锁的设定, 第⼆次加锁的时候, 就会阻塞等待. 直到第⼀次的锁被释放, 才能获取到第⼆ 个锁. 但是释放第⼀个锁也是由该线程来完成, 结果这个线程已经躺平了, 啥都不想⼲了, 也就⽆法进 ⾏解锁操作. 这时候就会 死锁

这样的锁称为 不可重⼊锁.
Java 中的 synchronized 是可重⼊锁, 因此没有上⾯的问题.
5.2 synchronized 使⽤⽰例
synchronized 本质上要修改指定对象的 "对象头". 从使⽤⻆度来看, synchronized 也势必要搭配⼀个 具体的对象来使⽤.
1) 修饰代码块: 明确指定锁哪个对象.
锁任意对象
public class SynchronizedDemo {private Object locker = new Object();public void method() {synchronized (locker) {}}
}锁当前对象
public class SynchronizedDemo {public void method() {synchronized (this) {}}
}2) 直接修饰普通⽅法: 锁的 SynchronizedDemo 对象
public class SynchronizedDemo {public synchronized void methond() {}
}
3) 修饰静态⽅法: 锁的 SynchronizedDemo 类的对象
public class SynchronizedDemo {public synchronized static void method() {}
}
我们重点要理解,synchronized 锁的是什么. 两个线程竞争同⼀把锁, 才会产⽣阻塞等待.
两个线程分别尝试获取两把不同的锁, 不会产⽣竞争

相关文章:

【JavaEE】多线程 (2) --线程安全
目录 1. 观察线程不安全 2. 线程安全的概念 3. 线程不安全的原因 4. 解决之前的线程不安全问题 5. synchronized 关键字 - 监视器锁 monitor lock 5.1 synchronized 的特性 5.2 synchronized 使⽤⽰例 1. 观察线程不安全 package thread; public class ThreadDemo19 {p…...

关于点胶机那些事
总结一下点胶机技术要点: 1:不论多复杂的点胶机,简单点,可以简化为:1:运控 2:点胶,3:检测 运控的目的就是负责把针头移到面板对应的胶路上,点胶即就是排胶&…...
Python | CAP - 累积精度曲线分析案例
CAP通常被称为“累积精度曲线”,用于分类模型的性能评估。它有助于我们理解和总结分类模型的鲁棒性。为了直观地显示这一点,我们在图中绘制了三条不同的曲线: 一个随机的曲线(random)通过使用随机森林分类器获得的曲线…...

ubuntu22.04安装swagboot遇到的问题
一、基本情况 系统:u 22.04 python: 3.10 二、问题描述 swagboot官方提供的安装路径言简意赅:python3 -m pip install --user snagboot 当然安装python3和pip是基本常识,这里就不再赘述。 可是在安装的时候出现如下提示说 Failed buildin…...

python每日一题——8无重复字符的最长子串
题目 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。 示例 2: 输入: s “bbbbb” 输出: 1 解释: 因为无重复字符的最长子串…...
【数据中台】开源项目(2)-Dbus数据总线
1 背景 企业中大量业务数据保存在各个业务系统数据库中,过去通常的同步数据的方法有很多种,比如: 各个数据使用方在业务低峰期各种抽取所需数据(缺点是存在重复抽取而且数据不一致) 由统一的数仓平台通过sqoop到各个…...

职场快速赢得信任
俗话说的好,有人的地方就有江湖。 国内不管是外企、私企、国企,职场环境都是变换莫测。 这里主要分享下怎么在职场中快速赢取信任。 1、找到让自己全面发展的方法 要知道,职场中话题是与他人交流的纽带,为了找到共同的话题&am…...

【SpringBoot3+Vue3】五【完】【实战篇】-前端(配合后端)
目录 一、环境准备 1、创建Vue工程 2、安装依赖 2.1 安装项目所需要的vue依赖 2.2 安装element-plus依赖 2.2.1 安装 2.2.2 项目导入element-plus 2.3 安装axios依赖 2.4 安装sass依赖 3、目录调整 3.1 删除部分默认目录下文件 3.1.1 src/components下自动生成的…...
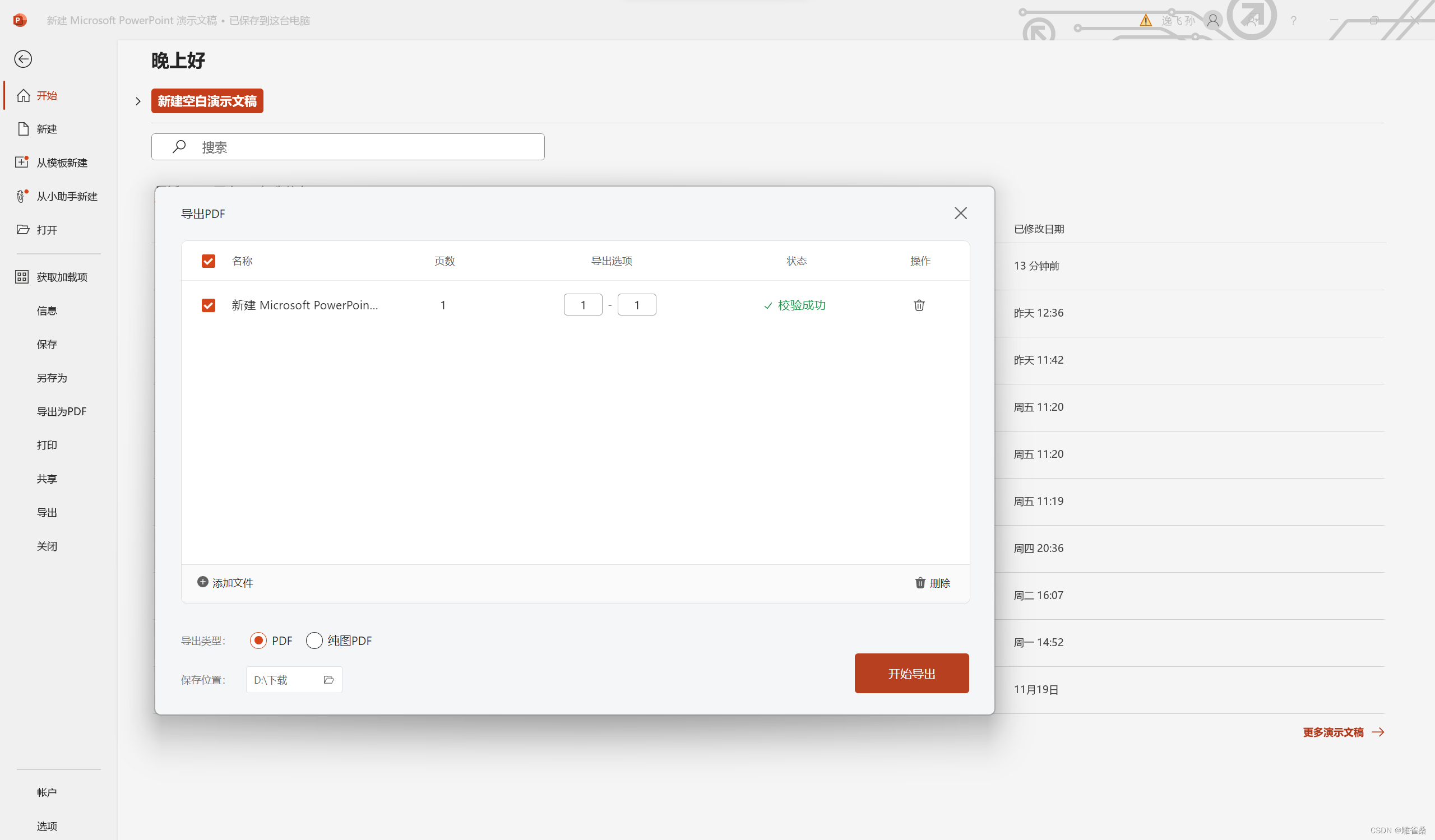
[LaTex]arXiv投稿攻略——jpg/png转pdf
一、将图片复制进ppt,右键单击图片选择设置图片格式,获取图片高度和宽度 二、选择“设计-幻灯片大小-自定义幻灯片大小” 三、设置幻灯片大小为图片大小 四、 选择“最大化” 五、 检查幻灯片大小是否与图像大小一致 六、导出为PDF...

使用Pytorch从零开始构建GRU
门控循环单元 (GRU) 是 LSTM 的更新版本。让我们揭开这个网络的面纱并探索这两个兄弟姐妹之间的差异。 您听说过 GRU 吗?门控循环单元(GRU)是更流行的长短期记忆(LSTM)网络的弟弟,也是循环神经网络&#x…...

【尚跑】2023宝鸡马拉松安全完赛,顺利PB达成
1、赛事背景 千年宝地,一马当先!10月15日7时30分,吉利银河2023宝鸡马拉松在宝鸡市行政中心广场鸣枪开跑。 不可忽视的是,这次赛事的卓越之处不仅在于规模和参与人数,还在于其精心的策划和细致入微的组织。为了确保每位…...

Mac nginx安装,通过源码安装教程
第一部分 安装参考网址: https://blog.csdn.net/a1004084857/article/details/128512612; 以上步骤执行完,进入找到sbin目录,查看下面是不是有nginx可执行文件,如果有在当前sbin下执行./nginx,就会发现NGINX已启动 第…...

TypeScript中的枚举是什么?
在TypeScript中,枚举(Enum)是一种用于定义一组有命名的常量值的数据类型。它们可以提供更具可读性和可维护性的代码。 枚举的作用是为一组相关的值提供一个易于理解和使用的命名空间。它们可以用于代表一系列可能的选项、状态或标志…...

进程并发-信号量经典例题-面包师问题
1 题目描述 面包师有很多面包和蛋糕,由N个销售人员销售。每个顾客进店后先取一个号,并且等着叫号。当一个销售人员空闲下来,就叫下一个号。试用信号量的P、V操作设计该问题的同步算法,给出所用共享变量(如果需要&…...
)
c语言练习12周(11~15)
编写double fun(int a[],int n)函数,计算返回评分数组a中,n个评委打分,去掉一个最高分去掉一个最低分之后的平均分 题干编写double fun(int a[],int n)函数,计算返回评分数组a中,n个评委打分,去掉一…...

Java 实现视频转音频功能
在实际开发中,我们经常需要处理各种多媒体文件。本文将介绍如何使用 Java 语言实现将视频文件转换为音频文件的功能。我们将使用 FFmpeg 工具来进行视频转换操作,并通过 Java 的 ProcessBuilder 实现调用系统命令执行 FFmpeg 的功能。 准备工作 首先,我们需要确保系统中已安…...
可以在Playgrounds或Xcode Command Line Tool开始学习Swift
一、用Playgrounds 1. App Store搜索并安装Swift Playgrounds 2. 打开Playgrounds,点击 文件-新建图书。然后就可以编程了,如下: 二、用Xcode 1. 安装Xcode 2. 打开Xcode,选择Creat New Project 3. 选择macOS 4. 选择Comman…...

IDC最新报告,增速减缓+AI增势,阿里云视频云中国市场第一
国际权威数据公司IDC发布 《中国视频云市场跟踪(2023 H1)》报告 自2018年至今,阿里云持续保持 中国视频云整体市场第一 整体市场占比达24.4% 01 第一之外,低谷之上 近期,国际权威数据公司IDC最新发布了《中国视频…...

常见状态码
欢迎大家到我的博客浏览。常见状态码 | YinKais Blog 常见状态码<!--more--> 1、200 200:服务器已经接收了请求,但处理还没有完成。 204:服务器已经成功处理了请求,但相应中没有任何返回内容。比如 DELETE 请求。 206&…...

Spring原理——基于xml配置文件创建IOC容器的过程
Spring框架的核心之一是IOC,那么我们是怎么创建出来的Bean呢? 作者进行了简单的总结,希望能对你有所帮助。 IOC的创建并不是通过new而是利用了java的反射机制,利用了newInstance方法进行的创建对象。 首先,我们先定义…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

