1005. K 次取反后最大化的数组和
原题链接:1005. K 次取反后最大化的数组和
思路:
先把数组排序好,然后直接从下标0(最小的负数)开始反转,那么接下来有两种情况:
1.负数反转完了,k还有剩余。此时因为nums内全部都是正数,所以我们只需要将nums再次排序,然后反复对nums[0]进行k此反转即可。
2.负数还没反转完,k没有剩余了。此时直接遍历nums每个元素进行累得出和即可。
全代码:
class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {//先排序,这样最小的都在左边 最大的在右边sort(nums.begin(),nums.end());//负数 先把最小负数反转//所有负数反转完后,剩余次数反转0或最小正数int sum = 0;for(int i = 0; i < nums.size(); i++){if(nums[i] < 0 && k > 0){//取反一次k--nums[i] = nums[i] * -1;k--;}}sort(nums.begin(),nums.end());while(k--){nums[0] *= -1;}for(int i = 0; i < nums.size();i++){sum+= nums[i];}return sum;}
};
相关文章:

1005. K 次取反后最大化的数组和
原题链接:1005. K 次取反后最大化的数组和 思路: 先把数组排序好,然后直接从下标0(最小的负数)开始反转,那么接下来有两种情况: 1.负数反转完了,k还有剩余。此时因为nums内全部都是正数,所以我…...
【云原生】什么是 Kubernetes ?
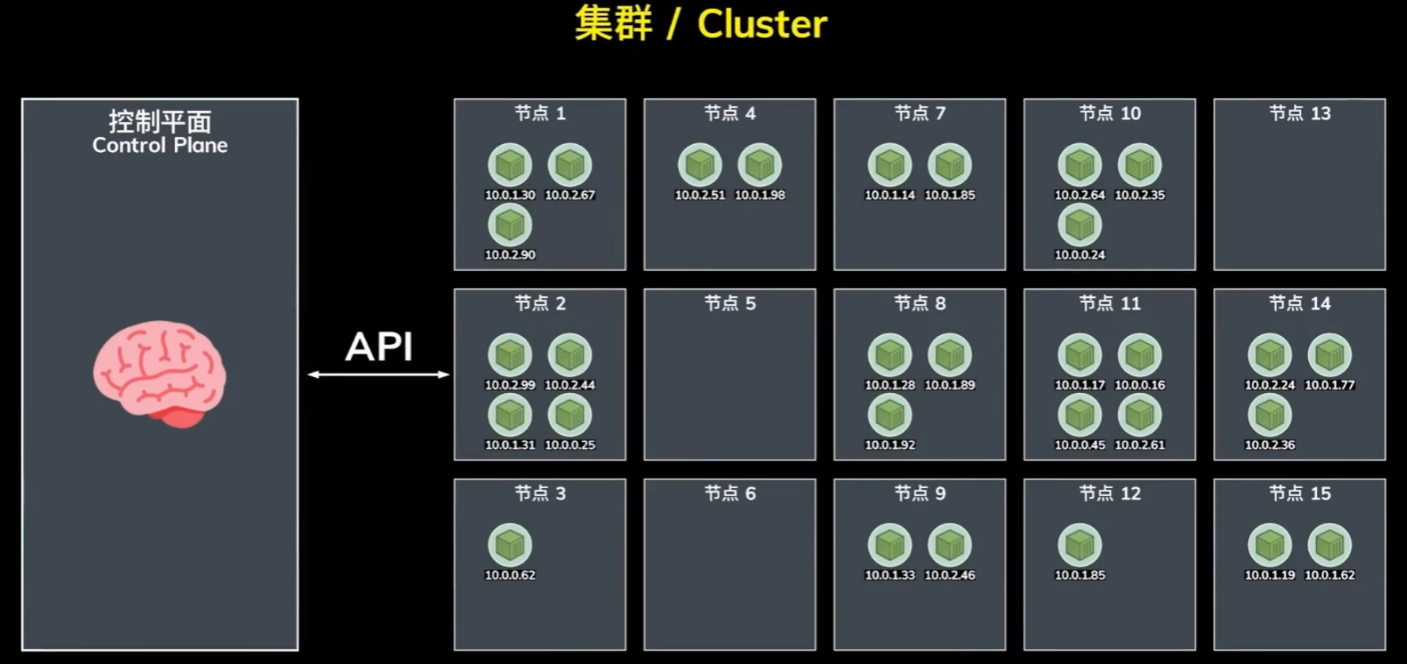
什么是 Kubernetes ? Kubernetes 是一个开源容器编排平台,管理着一系列的 主机 或者 服务器,它们被称作是 节点(Node)。 每一个节点运行了若干个相互独立的 Pod。 Pod 是 Kubernetes 中可以部署的 最小执行单元&#x…...

自建CA实战之 《0x01 Nginx 配置 https单向认证》
自建私有化证书颁发机构(Certificate Authority,CA)实战之 《0x01 Nginx 配置 https单向认证》 上一篇文章我们介绍了如何自建私有化证书颁发机构(Certificate Authority,CA),本篇文章我们将介…...

《QT从基础到进阶·三十八》QWidget实现炫酷log日志打印界面
QWidget实现了log日志的打印功能,不仅可以在界面显示,还可以生成打印日志。先来看下效果,源码放在文章末尾: LogPlugin插件类管理log所有功能,它可以获取Log界面并能打印正常信息,警告信息和错误信息&…...
JVM的小知识总结
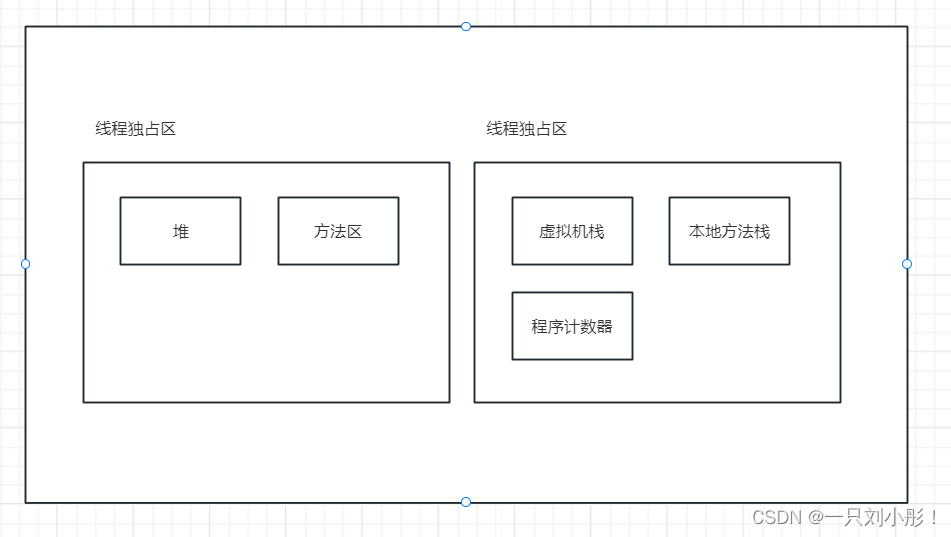
加载时jvm做了这三件事: 1)通过一个类的全限定名来获取该类的二进制字节流 什么是全限定类名? 就是类名全称,带包路径的用点隔开,例如: java.lang.String。 即全限定名 包名类型 非限定类名也叫短名,就…...
深入理解JVM虚拟机第二十六篇:详解JVM当中的虚方法和非虚方法,并从字节码指令的角度去分析虚方法和非虚方法
😉😉 学习交流群: ✅✅1:这是孙哥suns和树哥给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Spring...应用和源码级别的视频资料 🥭🥭3:QQ群:583783824 📚📚 微信:DashuDeveloper拉你进微信群,免费领取! 一:非虚方法和虚方法 方法…...

ElasticSearch的日志配置
ElasticSearch默认情况下使用Log4j2来记录日志,日志配置文件的路径为$ES_HOME/config/log4j2.properties,配置方法见Log4j2的官方文档。 参考path-settings,通过指定path.logs,可以指定日志文件的保存路径。 在日志配置文件$ES_…...

SQL Injection (Blind)`
SQL Injection (Blind) SQL Injection (Blind) SQL盲注,是一种特殊类型的SQL注入攻击,它的特点是无法直接从页面上看到注入语句的执行结果。在这种情况下,需要利用一些方法进行判断或者尝试,这个过程称之为盲注。 盲注的主要形式有…...

NX二次开发UF_CURVE_ask_trim 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_ask_trim Defined in: uf_curve.h int UF_CURVE_ask_trim(tag_t trim_feature, UF_CURVE_trim_p_t trim_info ) overview 概述 Retrieve the current parameters of an a…...
linux的netstat命令和ss命令
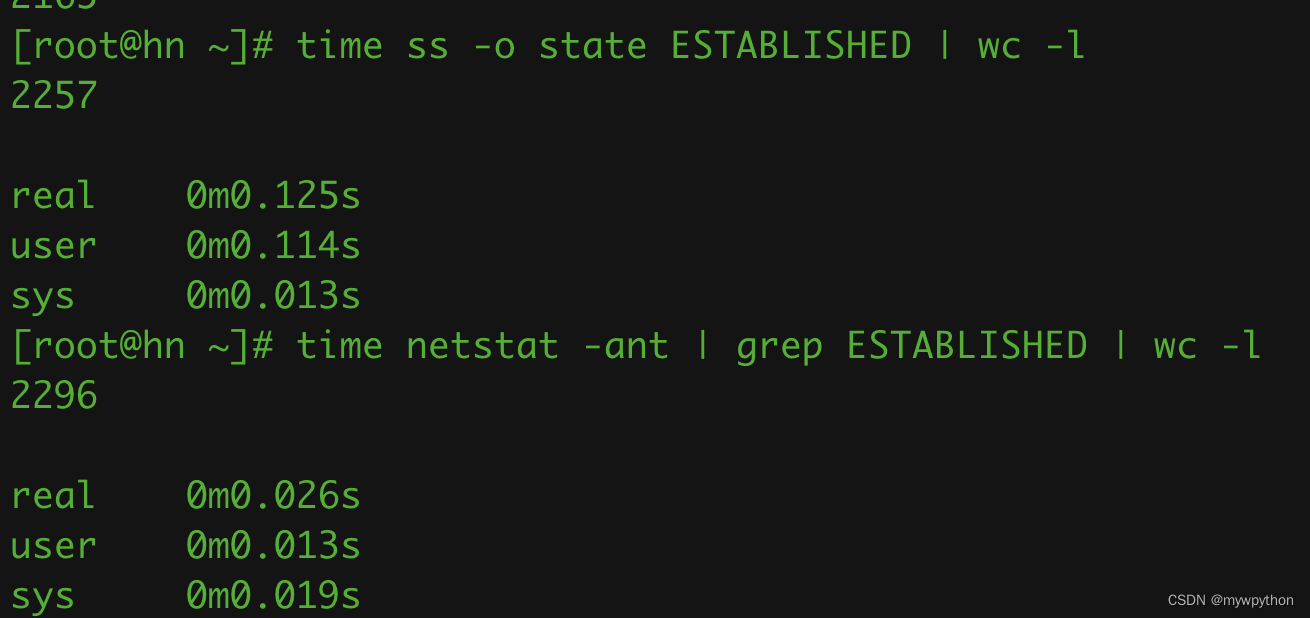
1. 网络状态 State状态LISTENING监听中,服务端需要打开一个socket进行监听,侦听来自远方TCP端口的连接请求ESTABLISHED已连接,代表一个打开的连接,双方可以进行或已经在数据交互了SYN_SENT客户端通过应用程序调用connect发送一个…...
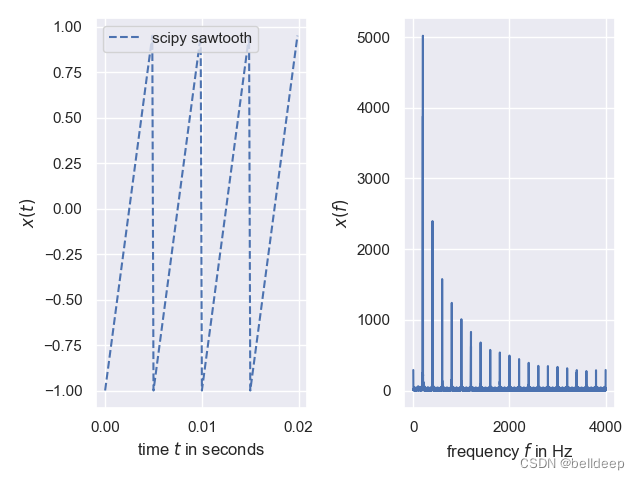
python:傅里叶分析,傅里叶变换 FFT
使用python进行傅里叶分析,傅里叶变换 FFT 的一些关键概念的引入: 1.1.离散傅里叶变换(DFT) 离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心&…...

云原生系列Go语言篇-编写测试Part 2
基准测试 确定代码是快或慢非常复杂。我们不用自己计算,应使用Go测试框架内置的基准测试。下面来看第15章的GitHub代码库sample_code/bench目录下的函数: func FileLen(f string, bufsize int) (int, error) {file, err : os.Open(f)if err ! …...

CMake Error:No targets specified and no makefile found
在适用cmake构建项目的时候,突然遇到了这个报错 Make Error at CMakeLists.txt:1 (project): VERSION not allowed unless CMP0048 is set to NEW – Configuring incomplete, errors occurred! make: *** No targets specified and no makefile found. Stop. CMake…...

常见树种(贵州省):019滇白珠、杜茎山、苍山越桔、黄背越桔、贵州毛柃、半齿柃、钝叶柃、细枝柃、细齿叶柃木、土蜜树、山矾、胡颓子、檵木
摘要:本专栏树种介绍图片来源于PPBC中国植物图像库(下附网址),本文整理仅做交流学习使用,同时便于查找,如有侵权请联系删除。 图片网址:PPBC中国植物图像库——最大的植物分类图片库 一、滇白珠…...

java - 定时器
一、什么是定时器 定时器是指可以通过 Java 中的 Timer 类和 TimerTask 类所提供的功能来实现定期执行某些任务的工具。 标准库中提供了一个 Timer 类 . Timer 类的核心方法为 schedule . schedule 包含两个参数 . 第一个参数指定即将要执行的任务代码 , 第二个参数指定多…...

jQuery【菜单功能、淡入淡出轮播图(上)、淡入淡出轮播图(下)、折叠面板】(五)-全面详解(学习总结---从入门到深化)
目录 菜单功能 淡入淡出轮播图(上) 淡入淡出轮播图(下) 折叠面板 菜单功能 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><…...

攻防非对称问题| 当前企业面临的网络攻防非对称问题及其解决途径
随着信息技术的不断发展,网络已经成为我们日常生活和商业活动中不可或缺的一部分。然而,随之而来的是网络安全问题的不断升级。网络攻防非对称问题是当前亟待解决的一个复杂而严峻的挑战。其主要的表现是攻击成本远低于防御成本以及相同投入带来的攻击能…...

Java多线程二-线程安全
1、线程安全问题 多个线程,同时操作同一个共享资源的时候,可能会出现业务安全问题。 2、实例:取钱的线程安全问题 2.1、场景 小明和小红是夫妻,他们有个共同账户,余额是十万元,如果两人同时取钱并且各自取…...

Rust个人学习之结构体
第一反应,Rust结构体跟python的很像,不知道感觉对不对; 书中提到第一反应,Rust结构体跟python的很像,不知道感觉对不对; 书中提到:结构体是一种自定义数据类型,它允许命名多个相关的…...

kafka详细讲解与安装
Kafka是一种分布式流处理平台,具有高吞吐量、可扩展性和容错性。它最初由LinkedIn开发,现已成为Apache软件基金会的顶级项目。Kafka广泛应用于实时数据流处理、日志收集、消息队列等场景。 以下是关于Kafka的简要讲解和安装步骤: 一、Kafka…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
