2023年中国边缘计算网关现状及发展趋势分析[图]
边缘计算网关是一种可以在设备上运行本地计算、消息通信、数据缓存等功能的工业智能网关,可以在无需联网的情况下实现设备的本地联动以及数据处理分析。边缘计算网关是一种连接物联网设备和云端服务的关键技术,它可以在设备和云端之间建立一个安全、高效的通信桥梁。边缘计算网关具有接口丰富,支持海量连接,数据采集和数据清洗,支持MQTT协议,支持多种工业通讯规约,支持web配置方式,支持云端远程配置等功能。
边缘计算网关分类

资料来源:共研产业咨询(共研网)
边缘网关充当终端设备与云端服务器之间的中间层,并负责从终端设备采集数据,对其进行处理和存储,并向云端服务器发送经过处理和封装后的数据。通过与物联网设备相连,边缘网关可以实现对设备的实时控制和监测,并对数据进行分析和决策。
边缘计算网关的优势表现在可以本地处理和存储数据、保障数据安全和隐私性,同时还能本地控制设备以及提供云端服务,2022年中国边缘计算网关市场规模同比增长57.75%。
2018-2023年中国边缘计算网关市场规模及增速
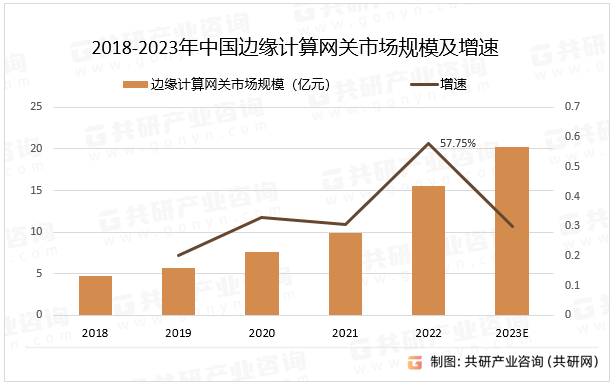
资料来源:共研产业咨询(共研网)
2023-2029年中国边缘计算网关行业全景调研及投资战略报告中显示:随着中国数据量的大规模增长,对于大数据的处理和运算能力的要求逐渐提高,下游对于边缘计算硬件设备的需求在逐渐提升,会吸引更多的市场进入者,市场竞争会进一步加剧。边缘计算网关领域大部分中小企业从事的多为领域中低端产品的生产,利润率有限,能够突破核心技术的企业有望占据更多市场份额,例如三旺通信等企业凭借强劲边缘计算能力及高性价比的产品,有望实现市场份额快速增长。
中国边缘计算网关市场发展趋势

资料来源:共研产业咨询(共研网)
相关文章:

2023年中国边缘计算网关现状及发展趋势分析[图]
边缘计算网关是一种可以在设备上运行本地计算、消息通信、数据缓存等功能的工业智能网关,可以在无需联网的情况下实现设备的本地联动以及数据处理分析。边缘计算网关是一种连接物联网设备和云端服务的关键技术,它可以在设备和云端之间建立一个安全、高效…...
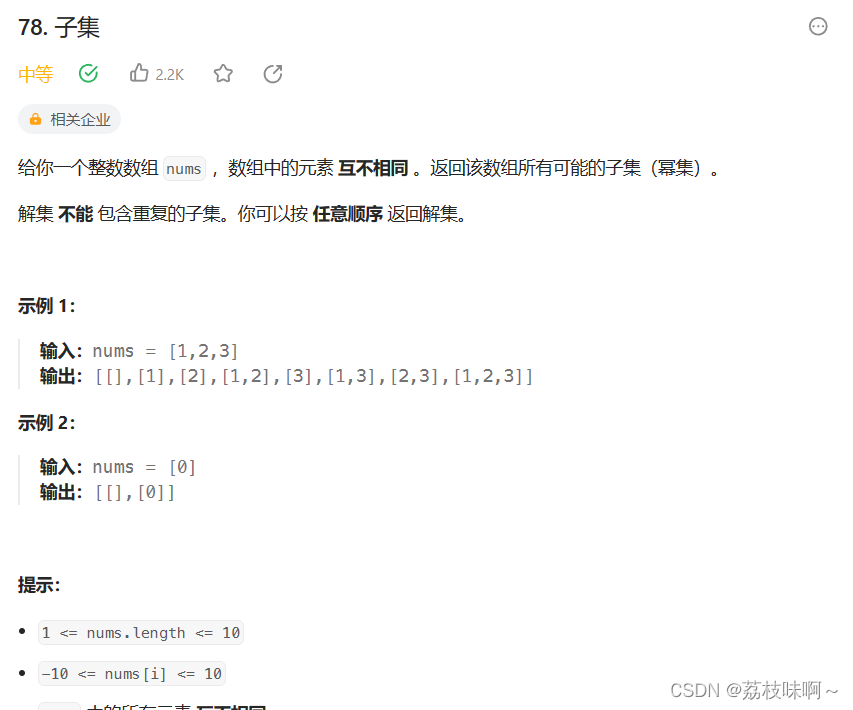
LeetCode78.子集
这道题如果用暴力法几乎是不可能解出来的,因为情况太复杂了,但是一旦用上递归回溯就会轻松很多,先上代码: class Solution {List<List<Integer>> result new ArrayList<List<Integer>>();List<Integ…...

不是默认进入Linux|总是自动进入windows系统
问题描述 不是默认进入Linux系统无法主动出现boot引导自动进入windows系统 尝试无效 修复引导无效重装Grub无效重装系统无效 环境 Ubuntu 22.04 LST微星主板 解决方案 修改引导顺序: 开机狂按Del键,进入BIOS系统,左侧Settings 设置&…...
)
【面经八股】搜广推方向:常见面试题(二)
【面经&八股】搜广推方向:常见面试题(二) 文章目录 【面经&八股】搜广推方向:常见面试题(二)1. FTRL 是什么?(Follow The Regularized Leader)2. 梯度下降方法3. 推荐系统中常见的Embedding方法有哪些?4. Embedding与推荐系统有哪些结合5. FM 和 FFM6. FNN7. 深…...

机器学习与药物筛选的心得体会
机器学习在药物设计里面的应用可以说还是比较常见的,尤其是搞计算的都会或多或少的涉及到这块。比如国内做这块比较多的,浙江大学的侯廷军教授,北京化工大学的闫爱霞教授,华东理工大学的几个做模拟计算的老师,上海药物…...

初识数据结构
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 熬过了我们不想要的生活…...
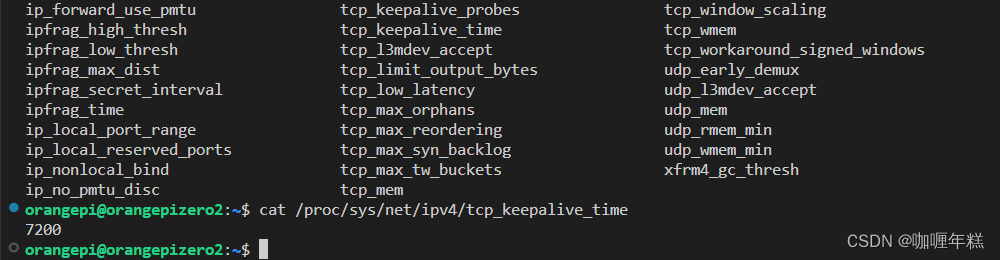
【阿里云】图像识别 智能分类识别 增加网络控制功能点(三)
一、增加网络控制功能 实现需求TCP 心跳机制解决Soket异常断开问题 二、Linux内核提供了通过sysctl命令查看和配置TCP KeepAlive参数的方法。 查看当前系统的TCP KeepAlive参数修改TCP KeepAlive参数 三、C语言实现TCP KeepAlive功能 四、setsockopt用于设置套接字选项的系…...

LeetCode 统计美丽子字符串 II【质因子分解,前缀和,哈希表】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

第一百八十一回 如何绘制阴影效果
文章目录 1. 概念介绍2. 使用方法2.1 SegmentedButton2.2 ButtonSegment 3. 代码与效果3.1 示例代码3.2 运行效果 4. 内容总结 1. 概念介绍 我们在本章回中介绍的SegmentedButton组件是一种分段式按钮,它把多个按钮连接成一组显示,组内再对不同的按钮进…...
Qt5.15.2静态编译 VS2017 with static OpenSSL
几年前编译过一次Qt静态库:VS2015编译Qt5.7.0生成支持XP的静态库,再次编译,毫无压力。 一.环境 系统:Windows 10 专业版 64位 编译器:visual studio 2017 第三方工具:perl,ruby和python python用最新的3.x.x版本也是可以的 这三个工具都需要添加到环境变量,安装时勾选…...
试用 13 -- 数据时效性)
AIGC(生成式AI)试用 13 -- 数据时效性
数据时效性? 最新的数据,代表最新的状态,使用最新的数据也应该最有说服力。 学习需要时间,AIGC学习并接收最新数据的效果如何? 问题很简单,如何验证?这个需要找点更新快的对像进行验证。…...

Sass的嵌套CSS 规则详细教程
文章目录 前言父选择器的标识符&群组选择器的嵌套子组合选择器和同层组合选择器:>、和~嵌套属性后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Sass和Less 🐱👓博主在前端领域还有很多知识和…...
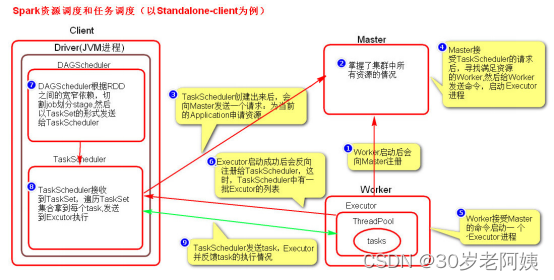
Spark---SparkCore(一)
一、术语与宽窄依赖 1、术语解释 1、Master(standalone):资源管理的主节点(进程) 2、Cluster Manager:在集群上获取资源的外部服务(例如:standalone,Mesos,Yarn) 3、Worker Node(standalone):资源管理的从节点(进程)或者说管理本机资源的…...

单链表原来是这样实现的!
文章目录 前言1. 链表的概念及结构1.1在链表里,每节“车厢”是什么样的呢?1.2为什么还需要指针变量来保存下⼀个节点的位置? 2. 单链表的实现1. 定义结构体(Seqlist)2. 打印函数(SLTPrint)小插曲,创建节点函数CreateNode3. 尾插函…...
excel一个单元格换行方法
要是在同一个单元格内输入文字输入不下的话,我们是可以进行同一个单元格换行设置的,而且换行的方法也是有很多种,下面我们就一起来看一下有哪些方法吧。 excel一个单元格换行方法: 方法一: 1、我们可以直接按下alte…...
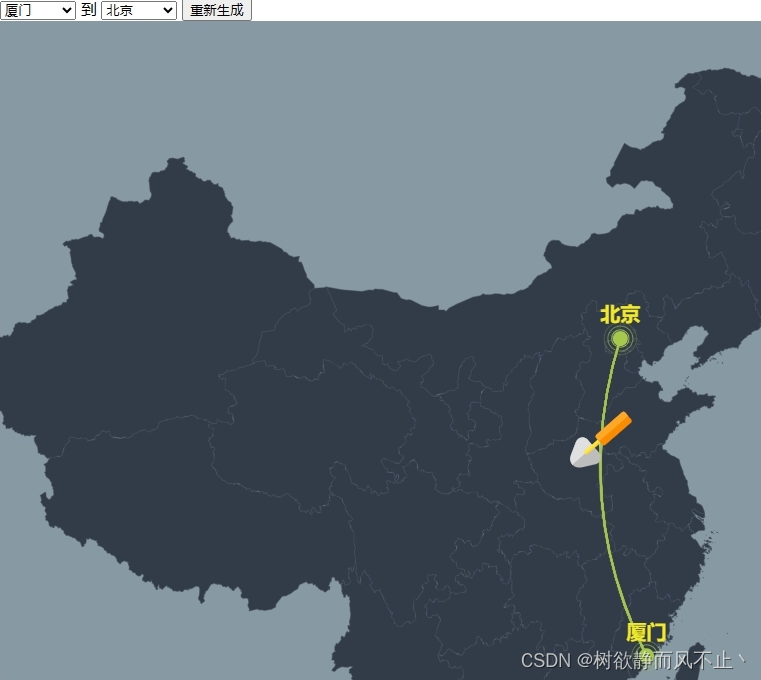
echart一键生成迁徙图
echart_move 介绍 echart迁徙图,选择起点和目的地生成迁徙图 软件架构 html echarts js 使用说明 将文件放到同一目录下打开index.html即可 默认是小飞机图标,如果想修改图标,将图片放到同一目录,如1.svg 代码修改为对应位…...

开发、测试、生产环境
开发环境:开发环境是程序猿们专门用于开发的服务器,配置可以比较随意, 为了开发调试方便,一般打开全部错误报告。简单讲就是项目尚且处于编码阶段,一般这时候会把代码放在开发环境中,不会放在生产环境中。 …...

红队攻防文库文章集锦
再救你一次,不要让欲望击溃你的意志 0.红队攻防 1.红队实战 红队攻防之特殊场景上线cs和msf CVE-2021-42287&CVE-2021-42278 域内提权 红队攻防之Goby反杀 红队攻防实战之钉钉RCE 红队攻防实战之从边界突破到漫游内网(无cs和msf) 红队攻防实战系列一之C…...

Vue框架学习笔记——键盘事件
文章目录 前文提要键盘事件(并不是所有按键都能绑定键盘事件)常用的按键不同的tab和四个按键keyCode绑定键盘事件(不推荐)Vue.config.keyCode.自定义键名 键码 神奇的猜想div标签和click.enterbutton标签和click.enter 前文提要 …...
Windows安装mysql8.0
官网地址:MySQL :: MySQL Community Downloads 选择相应版本信息下载 默认选择点击下一步 默认配置点击next 设置密码 默认配置...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
