【刷题笔记】加油站||符合思维方式
加油站
文章目录
- 加油站
- 1 题目描述
- 2 思路
- 3 解题方法
1 题目描述
https://leetcode.cn/problems/gas-station/
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
2 思路
正如大部分大佬所言,需要找到最小值所在的点。但是他们的代码写得有些含糊,我希望可以使用一种更加符合直觉的方式。
我们假设从i号加油站出发,然后用一张折线图表示到达每个加油站(最终返回i)时的剩余油量。x轴为加油站号,y轴为剩余油量。一开始的时候,剩余油量为0。首先来看一种可能的情况:
gas = [4, 3, 1, 2, 7, 4]
cost = [1, 2, 7, 3, 2, 5]
这里我们提供代码来表示从不同的站点出发,到达不同站点时候的剩余油量:
gas = [4,3,1,2,7,4]
cost = [1,2,7,3,2,5]
# 绘制
fig, axs = plt.subplots(1, 6, figsize=(20, 3))
for s in range(len(gas)):left_gas = [0 for _ in range(len(gas))]for i in range(len(gas)):left_gas[i] = (left_gas[i-1] if i > 0 else 0) + gas[(s + i) % len(gas)] - cost[(s + i) % len(gas)]left_gas.insert(0, 0)x = [(s + i) % len(gas) for i in range(len(gas))]x.append(s)axs[s].plot(range(len(gas) + 1), left_gas)axs[s].scatter(range(len(gas) + 1), left_gas)# 设置 x 轴刻度及标签axs[s].set_xticks(np.arange(len(gas) + 1))axs[s].set_xticklabels(x)# 绘制0刻度线axs[s].axhline(y=0, color='r', linestyle='-')# 将最低点标记出来,最低点的索引为left_gas.index(min(left_gas))axs[s].scatter(left_gas.index(min(left_gas)), min(left_gas), color='r')
plt.show()

你可以明显地看到从哪里出发,可以安全地开一圈了。(红线为0刻度线,红色点为最小点)
那么我们再举一个不可能开一圈的例子:
gas = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] # 0~9号加油站的油量
cost = [10, 9, 8, 7, 6, 5, 4, 3, 2, 11] # 0~9号加油站到下一站的消耗
其对应图像为

我这里也提供对应的绘图代码:
import matplotlib.pyplot as plt
import numpy as npgas = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] # 0~9号加油站的油量
cost = [10, 9, 8, 7, 6, 5, 4, 3, 2, 11] # 0~9号加油站到下一站的消耗# 绘制
# fig, axs = plt.subplots(1, 10, figsize=(20, 3))
# 上下两行,每行5个子图
fig, axs = plt.subplots(2, 5, figsize=(20, 6))
for s in range(len(gas)):left_gas = [0 for _ in range(len(gas))]for i in range(len(gas)):left_gas[i] = (left_gas[i - 1] if i > 0 else 0) + gas[(s + i) % len(gas)] - cost[(s + i) % len(gas)]left_gas.insert(0, 0)x = [(s + i) % len(gas) for i in range(len(gas))]x.append(s)# 设置 x 轴刻度及标签axs[int(s / 5)][s % 5].set_xticks(np.arange(len(gas) + 1))axs[int(s / 5)][s % 5].set_xticklabels(x)axs[int(s / 5)][s % 5].plot(range(len(gas) + 1), left_gas)axs[int(s / 5)][s % 5].scatter(range(len(gas) + 1), left_gas)# 绘制0刻度线axs[int(s / 5)][s % 5].axhline(y=0, color='r', linestyle='-')# 将最低点标记出来,最低点的索引为left_gas.index(min(left_gas))axs[int(s / 5)][s % 5].scatter(left_gas.index(min(left_gas)), min(left_gas), color='r')# 最低点设置垂直虚线,只往下画axs[int(s / 5)][s % 5].axvline(x=left_gas.index(min(left_gas)), color='r', linestyle='--')
plt.show()
什么情况下能转完一圈? 即总油量大于等于总耗油量。
3 解题方法
其实就是根据直觉,创建一个长度为gas.length + 1(参考上面的图,走一圈回来,相当于一共gas.length+1个站点)的数组left_gas(剩余油量),i位置初始为0,表示为在站点i出发时,剩余油量(或者说,初始油量)为0。
每两个站点之间的增加或者减少量是一定的,即任何两点之间连线的斜率是不变的(gas[i] - cost[i]),只要我们让最低值大于等于0,就可以保证走一圈。怎么让最低值大于等于0?只要我们让最低值为出发点,不就能保证其为0了?也就是能够保证最低点大于等于0。
所以,我们只需要找到最低点即可。
我们设置小车从0号站点出发,然后我们计算每个站点的剩余油量:
class Solution(object):def canCompleteCircuit(self, gas, cost):res = [0 for _ in range(len(gas) + 1)] # 剩余油量,为什么是len(gas) + 1,参考图中的x轴min_index = 0 # 初始站点min_left = 0 # 初始油量for i in range(len(gas)):res[i + 1] = res[i] + gas[i] - cost[i] # 例如,站点1的时候,剩余油量=res[0] + gas[0] - cost[0]if res[i + 1] < min_left: # 记录最低点的值和索引min_left = res[i + 1]min_index = i + 1return -1 if res[-1] < 0 else min_index # 到达最最终点的时候,相当于所有的gas相加,然后减去所有的cost,# 如果返回开头的时候,剩余油量小于0,则返回-1
相比之下,leetcode很多大佬的代码让我有点迷茫(没有说大佬写得不好,只是我有点难理解):
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int sum = 0 ;int min_num = Integer.MAX_VALUE;int min_index = 0;for ( int i = 0 ; i < gas.length ; i ++){sum += gas[i] - cost[i];if(sum<=min_num && gas[(i+1)%gas.length] >0){min_index = i;min_num = sum;}}return sum < 0 ? -1 : (min_index +1 ) % gas.length;}
}
相关文章:

【刷题笔记】加油站||符合思维方式
加油站 文章目录 加油站1 题目描述2 思路3 解题方法 1 题目描述 https://leetcode.cn/problems/gas-station/ 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消…...

【ArcGIS Pro微课1000例】0037:ArcGIS Pro中模型构建器的使用---以shp批量转kml/kmz为例
文章目录 一、ArcGIS Pro模型构建器介绍二、shp批量转kml/kmz1. 打开模型构建器2. 添加工作空间4. 添加【创建要素图层】工具5. 添加【图层转kml】工具6. 输出文件命名7. 运行模型三、模型另存为1.py文件2. 保存为工具一、ArcGIS Pro模型构建器介绍 模型构建器是一种可视化编程…...

前端 vue 面试题(二)
文章目录 如何让vue页面重新渲染组件间通信vue为什么要mutation、 action操作插槽、具名插槽、作用域插槽vue编译使用的是什么库?vue怎么实现treeshakingwebpack实现treeshaking为什么只有es module 能支持 tree shaking mixin 的作用mixin的底层原理nexTick原理vue…...
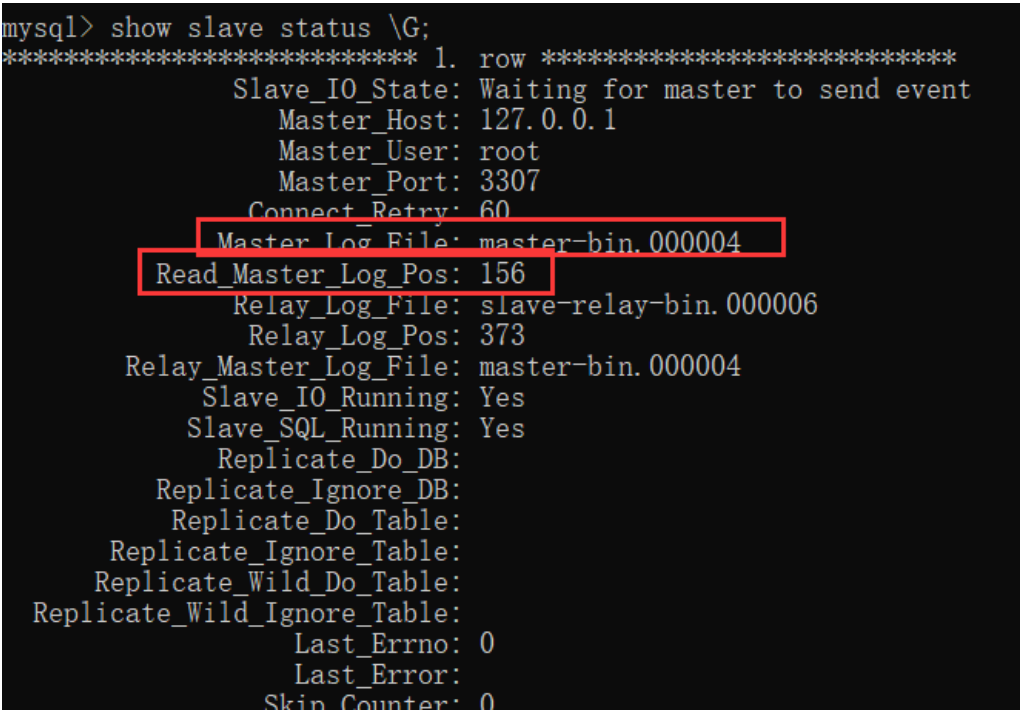
MySQL 高可用架构
MySQL 是实际生产中最常用的数据库,生产环境数据量极为庞大,对性能和安全要求很高,单机的 MySQL 是远远达不到的,所以必须搭建一个主从复制架构,同时可以基于一些工具实现高可用架构,在此基础上,…...

JVM虚拟机:G1垃圾回收器的日志分析
本文重点 本文我们将学习G1垃圾回收器的日志 使用 执行命令 java -Xms20M -Xmx20M -XX:PrintGCDetails -XX:UseG1GC 类名 分析 前面我们学习了G1垃圾回收器,它的回收有三种可能: YGC FGC MixedGC GC pause表示STW,Evacuation表示复制对象,…...

解决视口动画插件jquery.aniview.js使用animate.css时无效的问题(最新版本网页视口动画插件的使用及没作用、没反应)
当网站页面元素进入视口时自动应用过渡效果。CSS过渡效果可以为网页添加动画效果,并提供了一种平滑的转换方式,使元素的变化更加流畅和生动。而通过jQuery插件来获取页面滚动位置决定合适调用动画效果。 一、官网 animate.css官网 一款强大的预设css3动…...

【挑战业余一周拿证】一、亚马逊云科技简介 - 第 3 节 - 云计算
第 3 节 - 云计算 在深入了解亚马逊云科技的各个部分之前,让我们先缩小视野,对云进行一个合理的定义。云计算就是通过互联网按需提供 IT 资源并采用按需付费定价模式,下面,我们将进行详细说明。 按需提供表示的是亚马逊云科技会在…...

4. 无向图的各连通分支
题目 求解无向图的各连通分支 输入: 第一行为图的节点数n(节点编号0至n-1,0<n<10) 从第二行开始列出图的边,-1表示输入结束 输出: 输出每个连通分支的广度优先搜索序列(从连通分支的最…...
)
《golang设计模式》第三部分·行为型模式-08-状态模式(State)
文章目录 1. 概念1.1 作用1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概念 1.1 作用 状态(State)指状态对象,用于封装上下文对象的特定状态行为,使得上下文对象在内部状态改变时能够改变其自身的行为。 1.1 角色…...
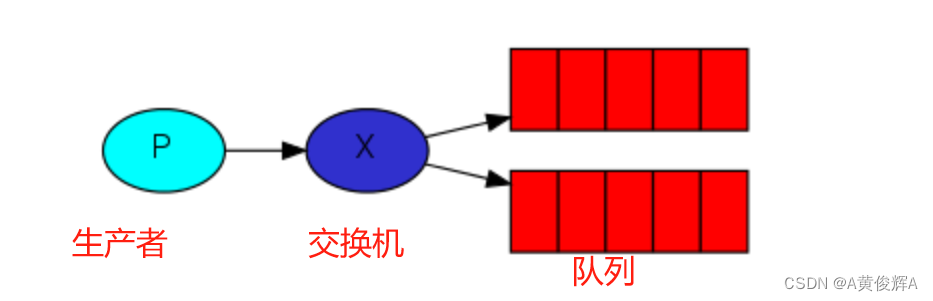
tp8 使用rabbitMQ(3)发布/订阅
发布/订阅 当我们想把一个消息,发送给 多个消费者的时候,我们把这种模式叫做发布/订阅模式,比如我们做两个消费者,其中一个消费者把消息写入磁盘中,别一个消费者把消息结果输出到屏幕上,就要用到发布订阅模…...
)
【nlp】3.4 Transformer论文复现:2. 编码器部分(规范化层、子层连接结构、编码器层)
3.4 Transformer论文复现:2. 编码器部分(规范化层、子层连接结构、编码器层) 2.6 规范化层2.6.1 规范化层的作用2.6.2 规范化层的代码实现2.6.3 规范化层总结2.7 子层连接结构2.7.1 子层连接结构2.7.2 子层连接结构的代码实现2.7.3 子层连接结构总结2.8 编码器层2.8.1 编码器…...
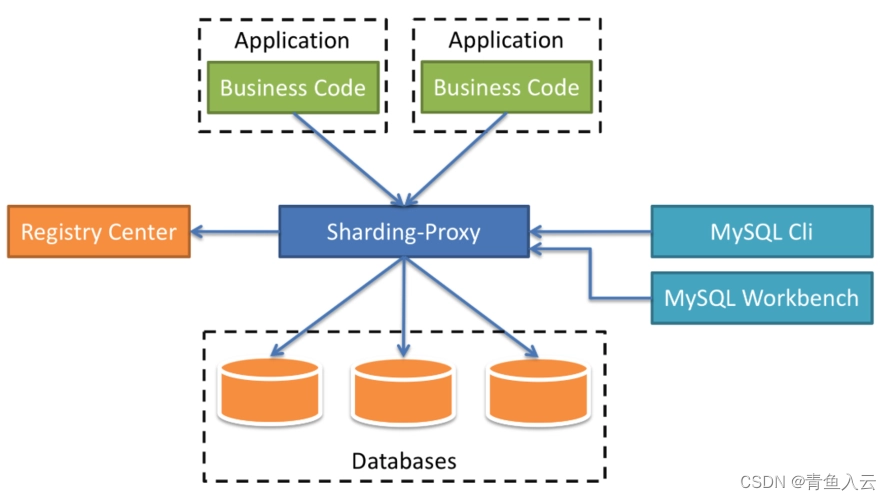
面试:ShardingSphere问题
文章目录 什么是ShardingSphere,它的主要功能是什么?ShardingSphere的核心模块有哪些?他们是如何工作的?ShardingSphere 的读写分离是如何实现的?如何配置ShardingSphere的数据分片策略?ShardingSphere支持…...

NX二次开发UF_CURVE_ask_offset_direction_2 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_ask_offset_direction_2 Defined in: uf_curve.h int UF_CURVE_ask_offset_direction_2(UF_STRING_p_t input_curves, double offset_direction_vector [ 3 ] , double dra…...
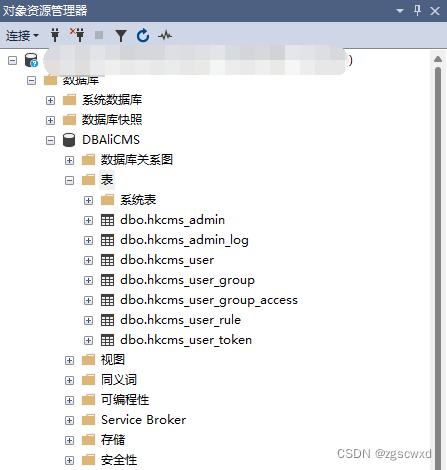
【研究中】sql server权限用户设置23.11.26
--更新时间2023.11.26 21:30 负责人:jerrysuse DBAliCMSIF EXISTS (select * from sysobjects where namehkcms_user)--判断是否存在此表DROP TABLE hkcms_user CREATE TABLE hkcms_user (id int primary key identity(1, 1),username char(32) NOT N…...
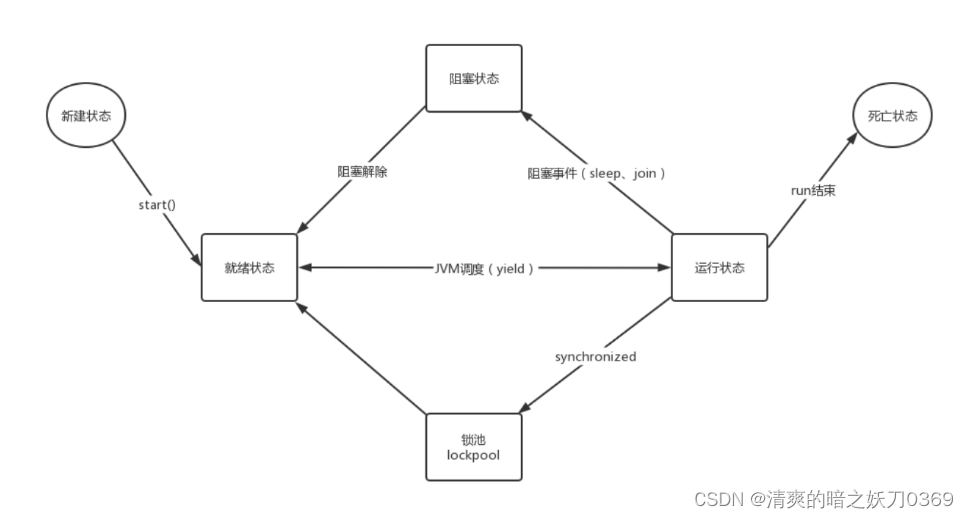
java多线程一
1、什么是线程 线程(Thread)是一条程序内部的一条执行流程。 程序中如果只有一条执行流程,那这个程序就是单线程的程序。 2、什么是多线程 多线程(multithreading),是指从软件或者硬件上实现多个线程并发执…...

电脑技巧:电脑常见蓝屏、上不了网等故障及解决办法
目录 一、电脑蓝屏 常见原因1: 病毒木马 常见原因2: 安装了不兼容的软件 二、电脑不能上网 常见原因1: 新装系统无驱动 常见原因2: DNS服务器异常 常见原因3: 硬件问题 三、电脑没声音 常见原因1: 未安装驱动 常见原因2: 硬件故障 四、电脑屏幕不显示 常见原因1: 显…...
大语言模型损失函数详解
我们可以把语言模型分为两类: 自动回归式语言模型:自动回归式语言模型在本质上是单向的,也就是说,它只沿着一个方向阅读句子。正向(从左到右)预测;反向(从右到左)预测。…...

Spring Boot 3 集成 Knife4j
基础环境 SpringBoot : 3.0.6 Java: jdk-17.0.5 Maven: 3.6.1依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xs…...

BetaFlight模块设计之三十六:SoftSerial
BetaFlight模块设计之三十六:SoftSerial 1. 源由2. API接口2.1 openSoftSerial2.2 onSerialRxPinChange2.3 onSerialTimerOverflow2.4 processTxState2.5 processRxState 3. 辅助函数3.1 applyChangedBits3.2 extractAndStoreRxByte3.3 prepareForNextRxByte 4. 总结…...

PC访问华为昇腾开发板的摸索过程
作者:朱金灿 来源:clever101的专栏 为什么大多数人学不会人工智能编程?>>> 最近要折腾华为昇腾开发板(官方名称叫:Atlas 200I DK)。先是按照官方教程折腾:Atlas200DK环境部署。我发现…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
