【数据结构初阶】树,二叉树
树,二叉树
- 1.树概念及结构
- 1.1树的概念
- 1.2 树的相关概念
- 1.3 树的表示
- 1.4 树在实际中的运用(表示文件系统的目录树结构)
- 2.二叉树概念及结构
- 2.1概念
- 2.2现实中的二叉树
- 2.3 特殊的二叉树
- 2.4 二叉树的性质
- 2.5 二叉树的存储结构
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
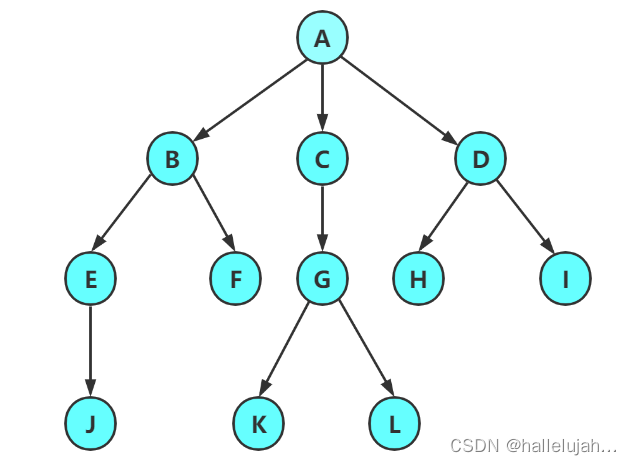
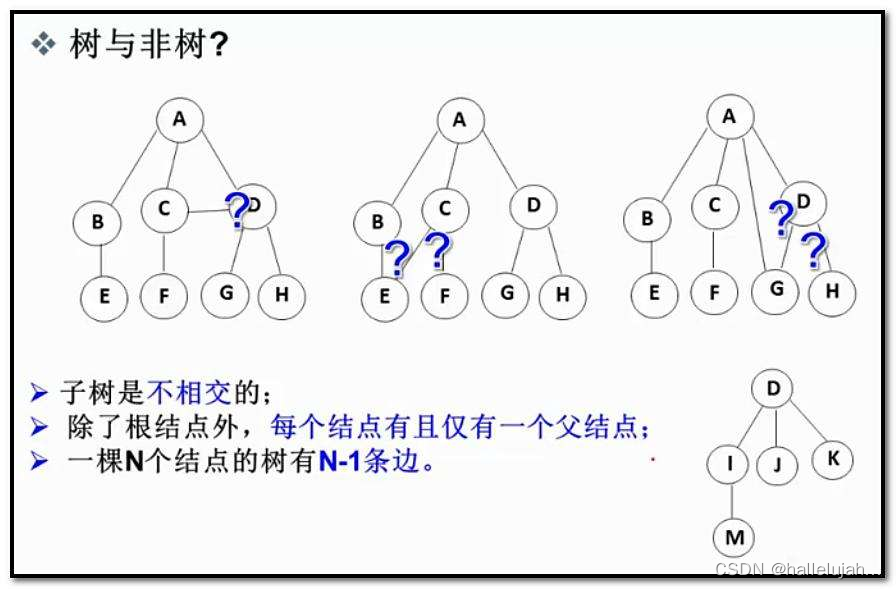
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关概念
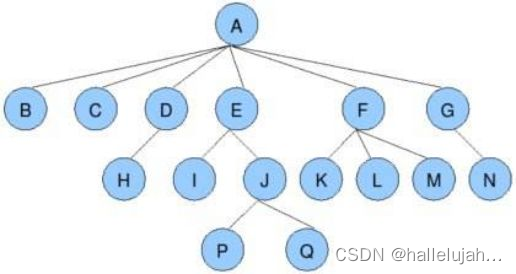
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
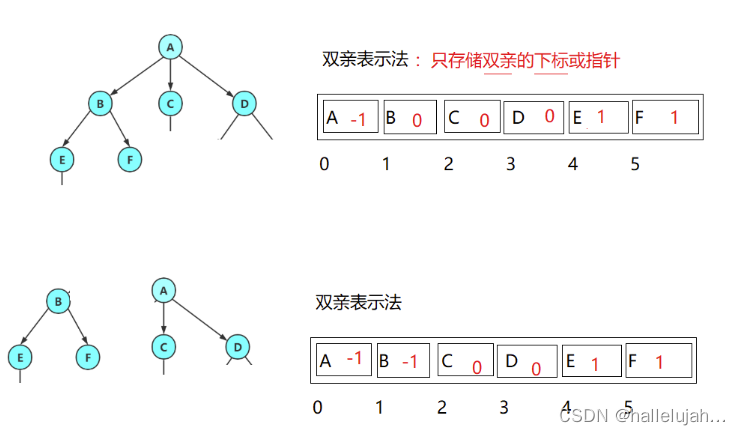
1.3 树的表示
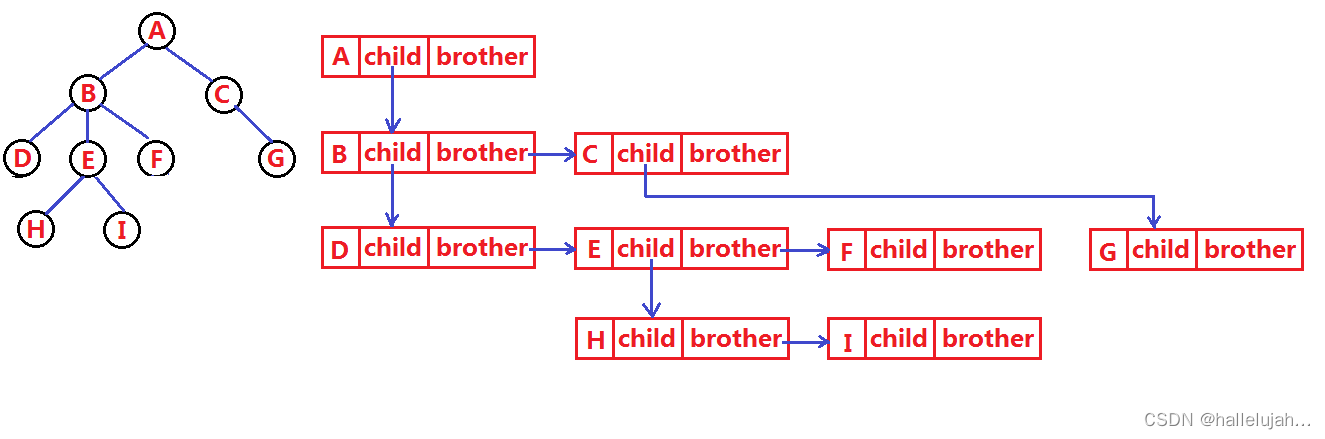
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
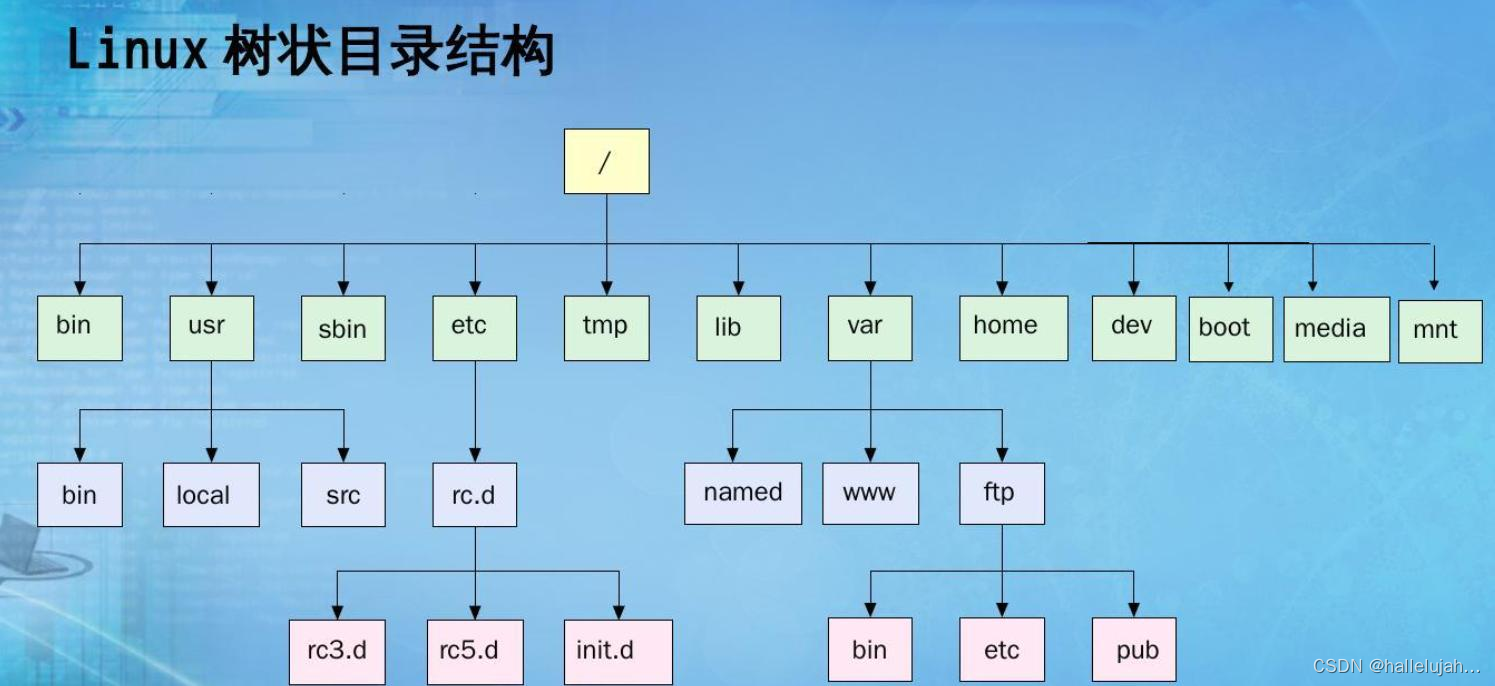
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
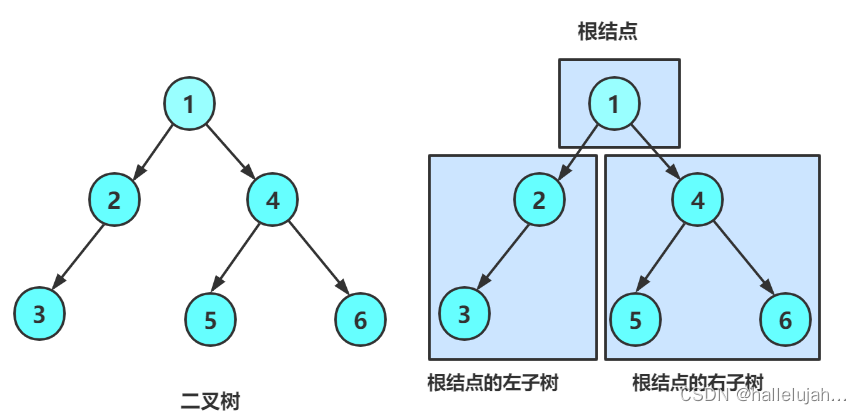
从上图可以看出: - 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
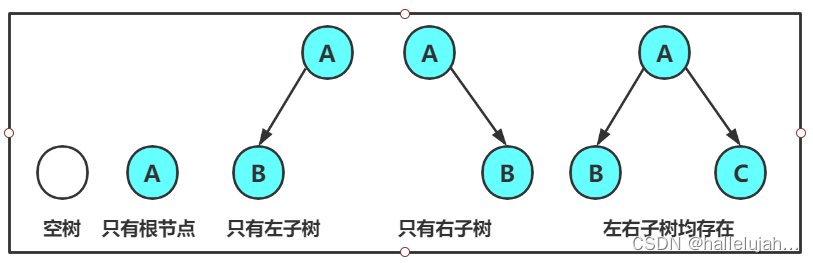
2.2现实中的二叉树


2.3 特殊的二叉树
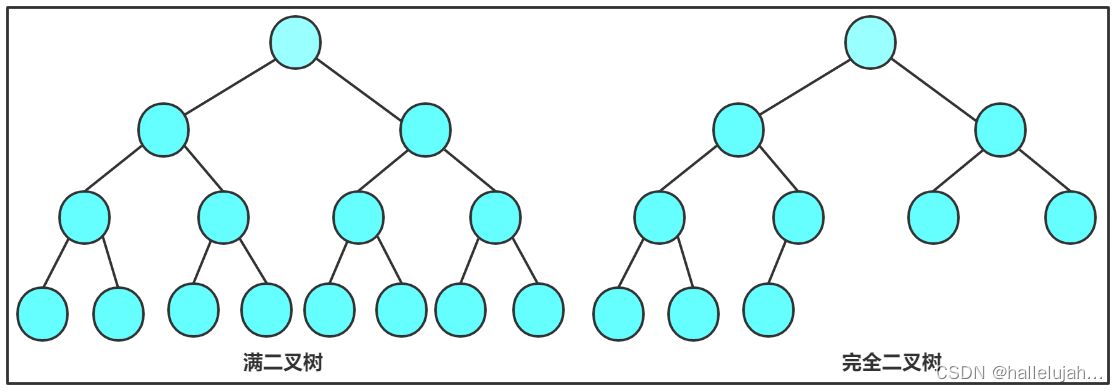
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.4 二叉树的性质

- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
题目练习
1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.下列数据结构中,不适合采用顺序存储结构的是( )
A 非完全二叉树
B 堆
C 队列
D 栈
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
5.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
答案:
1.B 2.A 3.A 4.B 5.B
2.5 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
-
顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
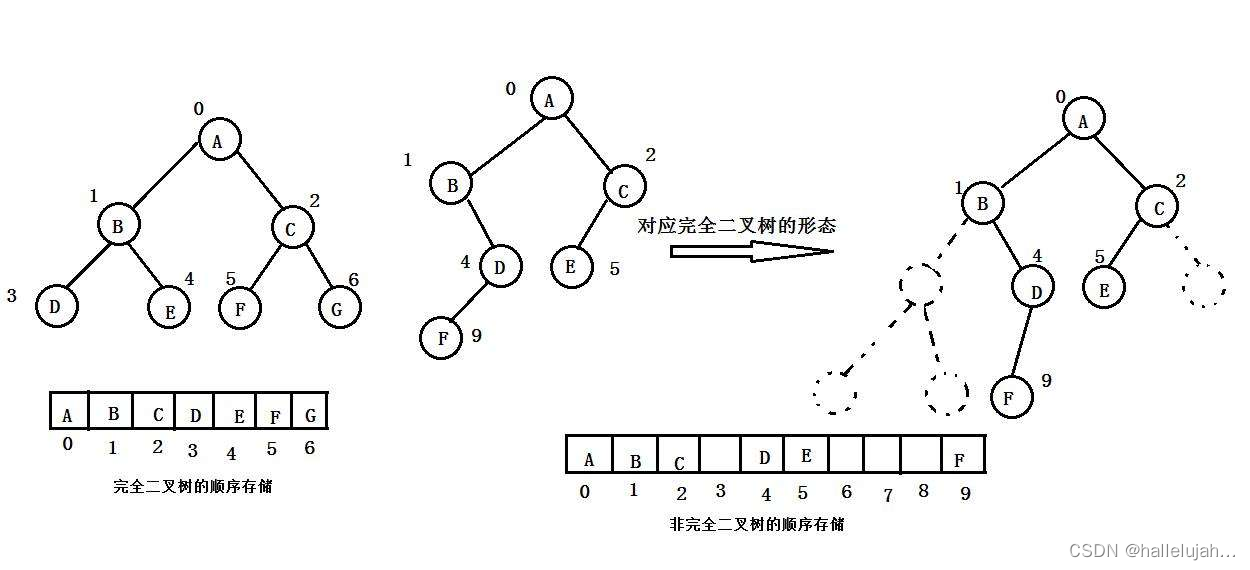
-
链式存储
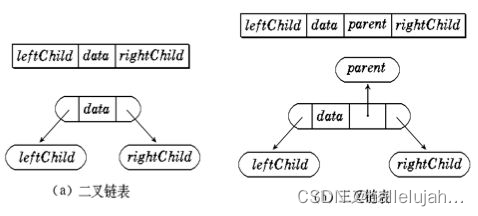
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面学到高阶数据结构如红黑树等会用到三叉链。
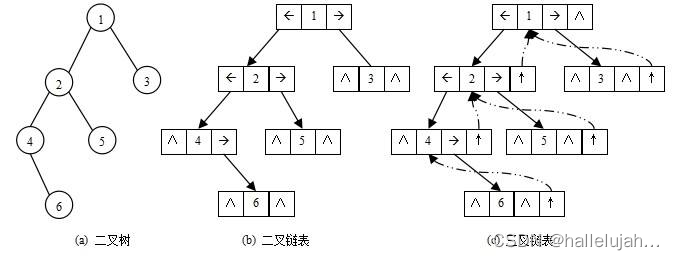
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
💘不知不觉,【数据结构初阶】树,二叉树学习告一段落。通读全文的你肯定收获满满,让我们继续为数据结构学习共同奋进!!!
相关文章:

【数据结构初阶】树,二叉树
树,二叉树 1.树概念及结构1.1树的概念1.2 树的相关概念1.3 树的表示1.4 树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构2.1概念2.2现实中的二叉树2.3 特殊的二叉树2.4 二叉树的性质2.5 二叉树的存储结构 1.树概念及结构 1.…...

HTML新手入门笔记整理:HTML常用标签总结表
HTML常用标签 标签 英文全称 语义 div division 区块(块元素) span span 区块(行内元素) p paragraph 段落 ol ordered list 有序列表 ul unordered list 无序列表 li list item 列表项 dl definition list 定义列表 dt definition term 定义术语 d…...
Linux7安装mysql数据库以及navicat远程连接mysql
1.下载地址:MySQL :: Download MySQL Community Server 2.创建mysql目录将压缩包上传到该目录 mkdir /opt/mysql cd /opt/mysql3.解压压缩包 gzip mysql-8.1.0-1.el7.x86_64.rpm-bundle.tar tar -zxvf mysql-8.1.0-1.el7.x86_64.rpm-bundle.tar.gz 4.前置检查 ch…...
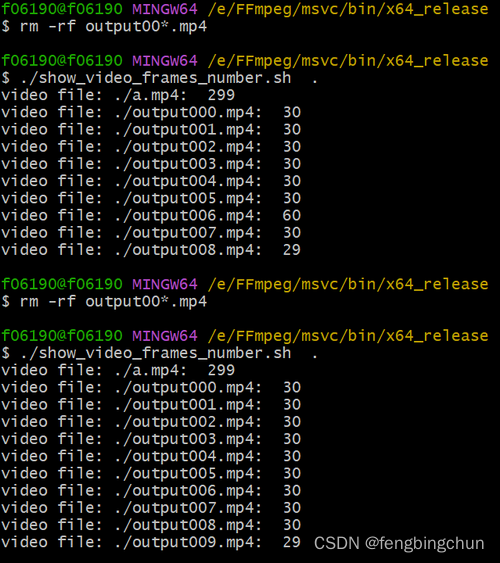
FFmpeg命令分隔视频
有一个视频如a.mp4,此视频采用帧率为30生成,共有299帧,这里通过FFmpeg命令分隔成1秒一个个的小视频,即每个小视频帧数为30帧。 用到的FFmpeg参数如下所示: (1).-i:指定输入视频文件的名称; (2).-c:指…...

开源与闭源
我的观点: 开源与闭源软件都有各自的优势和劣势,没有绝对的对错之分。.. 一、开源和闭源的优劣势比较 开源的好处与劣处 优势: 创新与合作:开源软件能够吸引更多的开发者参与到项目中来,促进创新和合作。开放的源代码…...

详解Python对Excel处理
Excel是一种常见的电子表格文件格式,广泛用于数据记录和处理。Python提供了多个第三方库,可以方便地对Excel文件进行读写、数据操作和处理。本文将介绍如何使用Python对Excel文件进行处理,并提供相应的代码示例和详细说明。 一、安装第三方库…...

docker compose搭建渗透测试vulstudy靶场示例
前言 渗透测试(Penetration test)即网络安全工程师/安全测试工程师/渗透测试工程师通过模拟黑客,在合法授权范围内,通过信息搜集、漏洞挖掘、权限提升等行为,对目标对象进行安全测试(或攻击)&am…...

Python基础教程:强大的Pandas数据分析库
Pandas是一个基于 NumPy 的非常强大的开源数据处理库,它提供了高效、灵活和丰富的数据结构和数据分析工具,当涉及到数据分析和处理时,使得数据清洗、转换、分析和可视化变得更加简单和高效。本文中,我们将学习如何使用Pandas来处理…...

【深入剖析K8s】容器技术基础(一):从进程开始说起
容器其实是一种特殊的进程而已。 可执行镜像 为了能够让这些代码正常运行’我们往往还要给它提供数据’比如我们这个加法程序所需要的输人文件这些数据加上代码本身的二进制文件放在磁盘上’就是我们平常所说的一个程序,也叫代码的可执行镜像(executablejmage&…...
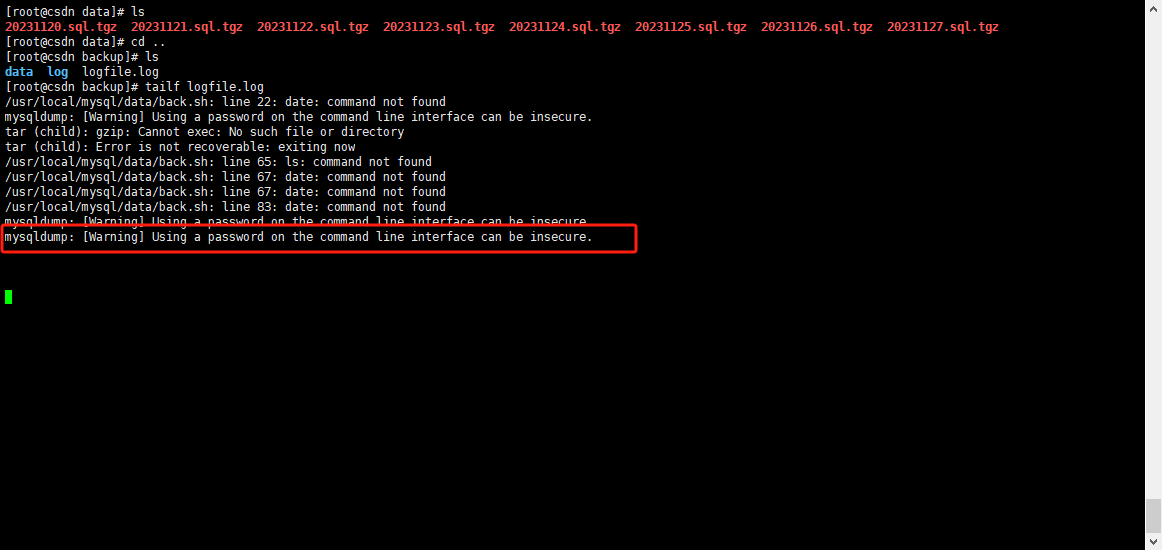
Mysql使用周期性计划任务定时备份,发现备份的文件都是空的?为什么?如何解决?
👨🎓博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 🐋 希望大家多多支…...
)
算法leetcode|90. 子集 II(rust重拳出击)
文章目录 90. 子集 II:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 90. 子集 II: 给你一个整数数组 nums ,其…...

git 泄露
得到flag有两种方法: 1、版本比对:git diff 用法:git diff <分支名1> <分支名2> 2、版本回退:git reset 用法:git reset --hard <分支名> python2 GitHack.py http://www.example.com/.git/ g…...
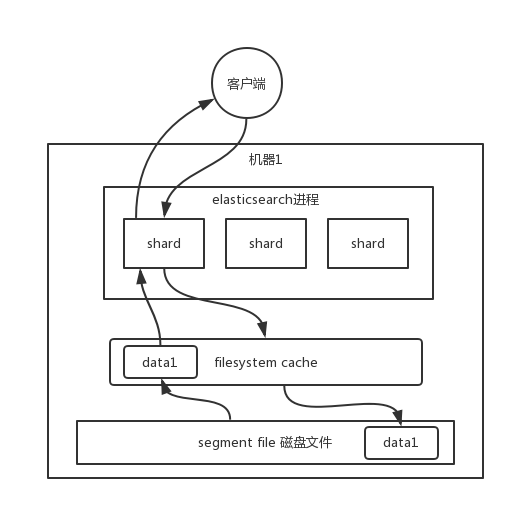
Elasticsearch知识
目录 Elasticsearch逻辑设计和物理设计 逻辑设计物理设计Elasticsearch原理 倒排索引文档的分析过程保存文档搜索文档写数据的底层原理 数据刷新(fresh)事务日志的写入ES在大数据量下的性能优化 文件系统缓存优化数据预热文档(Document&…...

极智芯 | 解读国产AI算力天数智芯产品矩阵
欢迎关注我的公众号 [极智视界],获取我的更多经验分享 大家好,我是极智视界,本文分享一下 解读国产AI算力天数智芯产品矩阵。 邀您加入我的知识星球「极智视界」,星球内有超多好玩的项目实战源码和资源下载,链接:https://t.zsxq.com/0aiNxERDq 天数智芯属于国产 GPGPU 阵…...

使用 OpenCV 发现圆角矩形的轮廓
OpenCV - 如何找到圆角矩形的矩形轮廓? 问题: 在图像中,我试图找到矩形对象的圆角轮廓。然而,我对两者的尝试 HoughLinesP 并 findContours 没有产生预期的结果。 我的目标是找到一个类似于以下形状的矩形: 。 代码: import cv2 import matplotlib.pyplot as plt…...
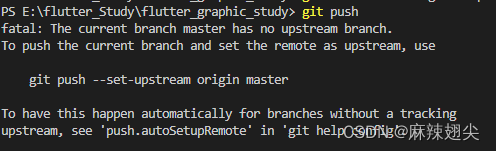
vscode项目推送到git
1、打开项目文件 打开文件后点击vs code左侧工具栏中第三个源代码管理图标,点击初始化仓库,此时会创建一个本地仓库会检查该项目中的文件变更 2、创建远程仓库 点击克隆/下载,复制HTTPS地址 3、添加远程地址 1)图形化操作 2…...

COMP2121 Discrete Mathematics
COMP2121 Discrete Mathematics 需要可WeChat: zh6-86...

【随笔记录】VMware搭建python开发环境
Vmware虚拟机总是连接不到网络。 环境为:笔记本WLAN 解决方法。 1.直接使用VMware 编辑->虚拟网络编辑器->恢复默认设置。 2.取消网卡的IP的dhcp获取,改为static。网关为提供IP的主机的网络IP(NAT模式) 3.windows打开共享网…...

基于C++实现水仙花数
1、水仙花数的连营 1.1、水仙花数 在学习程序设计课程时,大多数读者一定采用循环结构编写过求解水仙花数的程序。 【实例 1-1】水仙花数 一个三位整数(100~999),若各位数的立方和等于该数自身,则称其为“…...

关于一个类中引用两外一个类中的变量和方法,一个技巧可以提高开发效率
import static com.xx.xx.util.ext.xx.toJson; import static com.xx.xx.util.ext.smf.Cert.certMgrClient; 第一个引用一个方法,第二个引用一个变量, 引用后就可以直接通过变量名或者方法名就行使用,很方便,不要通过class.方式调…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
