visual Studio MFC 绘制单一颜色三角形、渐变颜色边框三角形、渐变填充三角形、边框渐变的正方形与填充渐变的正方形实例
MFC 绘制三角形
本文使用visual Studio MFC 平台实现绘制单一颜色三角形、渐变颜色边框三角形、渐变填充三角形、边框渐变的正方形与填充渐变的正方形.
关于基础工程的创建请参考Visual Studio 使用MFC 单文档工程绘制单一颜色直线和绘制渐变颜色的直线
文章目录
- MFC 绘制三角形
- 一、 绘制单一颜色三角形
- 二、 绘制边框颜色渐变的三角形
- 三、 绘制填充渐变色三角形
- 四、绘制渐变色边框正方形
- 五、绘制渐变色填充正方形
一、 绘制单一颜色三角形
通过dc.Polygon(pt, 3)绘制多边形.
在MFC(Microsoft Foundation Classes)中,dc.Polygon 函数用于在设备上下文(Device Context)中绘制多边形。这个函数的原型如下:
BOOL Polygon(const POINT* lpPoints,int nCount
);
参数解释:
lpPoints: 一个 POINT 结构体数组,表示多边形的顶点。每个 POINT 结构体包含 x 和 y 坐标,定义了多边形的一个顶点。nCount: 顶点的数量。
返回值:
- 如果函数成功,则返回非零值;如果函数失败,则返回零。
这个函数用给定的顶点数组在设备上下文中绘制一个多边形。代码片段中,pt[3] 是一个包含三个 CPoint 结构体的数组,表示一个三角形的三个顶点。然后,dc.Polygon(pt, 3) 调用绘制三角形。
CClientDC dc(this);
CPen pen(PS_SOLID, 4, RGB(255,182,193));//RGB(138, 100, 226) 表示紫罗兰色
CPen* oldPen = dc.SelectObject(&pen);//选择当前设备上下文的画笔为 pen,并将之前的画笔保存在 oldPen 中。这是为了在绘制完成后恢复原来的画笔
CPoint pt[3] = { CPoint(400,70),CPoint(800,70), CPoint(340,400) };//表示一个三角形的三个顶点坐标
dc.Polygon(pt, 3);// 使用 dc 绘制一个多边形,多边形的顶点由 pt 数组指
'CPen pen(PS_SOLID, 4, RGB(255, 182, 193))'
- CPen是MFC中表示画笔的类。
- PS_SOLID表示画笔风格为实线,4表示线宽,RGB(255, 182, 193)表示颜色为紫罗兰色。
实现效果如下
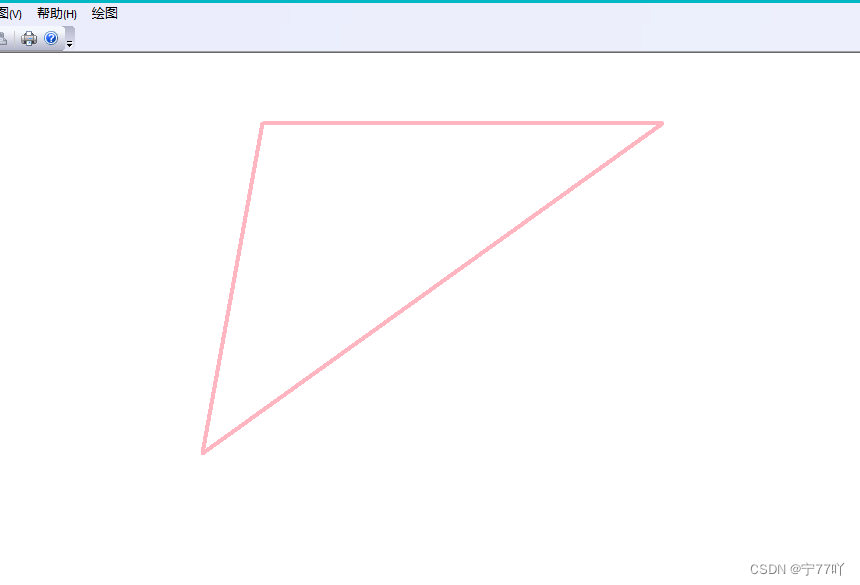
二、 绘制边框颜色渐变的三角形
使用 DrawLines 函数绘制了连接三个顶点的线条,从而形成了一个空心的三角形。画笔 Pen 使用渐变画刷作为颜色,实现了渐变色的效果.
GdiplusStartupInput gdiplusStartupInput;
ULONG_PTR gdiplusToken;//标识符号
GdiplusStartup(&gdiplusToken, &gdiplusStartupInput, NULL);
{// 创建 GDI+ 绘图对象Graphics graphics(GetSafeHwnd());// 定义三个渐变色Color color1(255, 255, 0); // 黄色Color color2(0, 255, 255); // 青色Color color3(255, 0, 255); // 粉色// 创建渐变画笔LinearGradientBrush brush(Point(0, 0), Point(800, 400), color1, color2);REAL positions[] = { 0.0f, 1.0f };Color colors[] = { color1, color2 };brush.SetInterpolationColors(colors, positions, 2);// 创建画笔Pen pen(&brush, 3);// 定义三角形的三个顶点PointF points[4] = { PointF(400.0f, 100.0f), PointF(800.0f, 100.0f), PointF(400.0f, 400.0f), PointF(400.0f, 100.0f) };// 使用画笔绘制空心的渐变色边的三角形graphics.DrawLines(&pen, points, 4);}
// 关闭 GDI+
GdiplusShutdown(gdiplusToken);
补充说明
LinearGradientBrush:表示线性渐变画笔的类。brush:创建的渐变画笔对象。
参数说明:
Point(0, 0):渐变的起始点,这里是窗口坐标 (0, 0)。Point(800, 400):渐变的终止点,这里是窗口坐标 (800, 400)。color1:起始颜色。color2:终止颜色。
这段代码的作用是创建一个从起始点 (0, 0) 到终止点 (800, 400) 的线性渐变,颜色从 color1(起始颜色)变化到 color2(终止颜色)。这样的渐变将用于后续的绘图操作,例如在绘图对象上绘制形状时,形状的颜色将沿着这个线性渐变进行变化。
实现效果
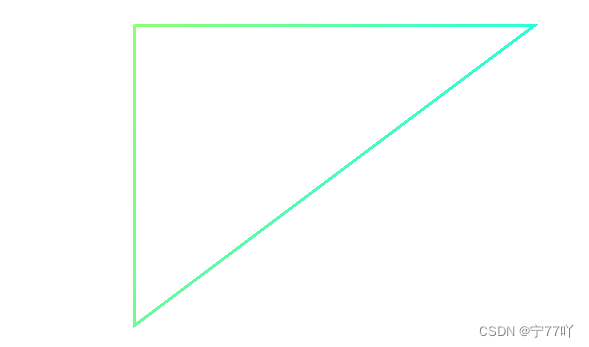
三、 绘制填充渐变色三角形
使用 FillPolygon 函数绘制了一个填充的渐变色三角形。画刷 brush 使用LinearGradientBrush 实现了渐变色的效果,然后通过 FillPolygon 函数填充三角形
// 创建 GDI+ 绘图对象
Graphics graphics(GetSafeHwnd());// 定义三个渐变色
Color color1(255, 255, 0); // 黄色
Color color2(0, 255, 255); // 青色
Color color3(255, 0, 255); // 粉色// 创建渐变画刷
LinearGradientBrush brush(Point(0, 0), Point(1000, 1000), color1, color2);REAL positions[] = {0.0f, 1.0f};
Color colors[] = {color1, color2};
brush.SetInterpolationColors(colors, positions, 2);// 定义三角形的三个顶点
PointF points[3] = {PointF(400.0f, 100.0f), PointF(800.0f, 100.0f), PointF(400.0f, 400.0f)};// 使用渐变画刷填充三角形
graphics.FillPolygon(&brush, points, 3);实现效果如下
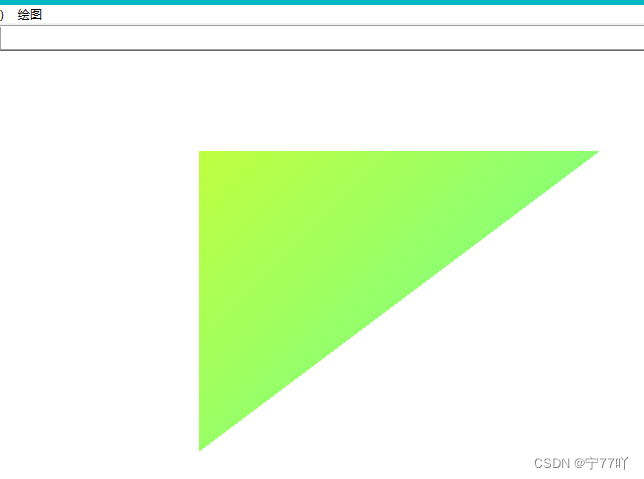
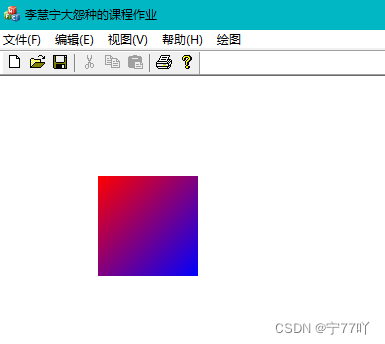
四、绘制渐变色边框正方形
如果你想绘制边框为渐变色的正方形,可以使用 DrawPolygon 函数,并指定 Pen 对象为渐变画笔。
// 创建 GDI+ 绘图对象
Graphics graphics(GetSafeHwnd());// 定义两个渐变色
Color color1(255, 0, 0); // 红色
Color color2(0, 0, 255); // 蓝色// 创建渐变画刷
LinearGradientBrush brush(Point(0, 0), Point(100, 100), color1, color2);REAL positions[] = {0.0f, 1.0f};
Color colors[] = {color1, color2};
brush.SetInterpolationColors(colors, positions, 2);// 定义正方形的四个顶点
PointF points[4] = {PointF(100.0f, 100.0f), PointF(200.0f, 100.0f), PointF(200.0f, 200.0f), PointF(100.0f, 200.0f)};// 创建渐变画笔
Pen gradientPen(&brush, 5.0f); // 5.0f 是画笔的宽度// 使用渐变画笔绘制正方形的边框
graphics.DrawPolygon(&gradientPen, points, 4);
在这个例子中,我们使用 DrawPolygon 函数绘制了正方形的边框,并且使用 Pen 对象 gradientPen 设置了渐变画笔。 Pen 的构造函数接受一个 Brush 对象,这里我们使用 LinearGradientBrush 作为画笔的颜色。
实现效果图.
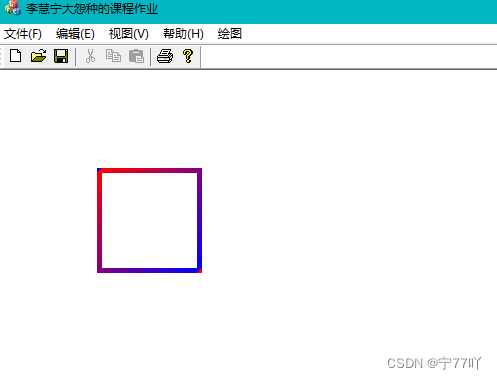
五、绘制渐变色填充正方形
要绘制一个填充的正方形,你可以使用 FillRectangle 函数。以下是一个示例代码片段:
// 创建 GDI+ 绘图对象
Graphics graphics(GetSafeHwnd());// 定义两个渐变色
Color color1(255, 0, 0); // 红色
Color color2(0, 0, 255); // 蓝色// 创建渐变画刷
LinearGradientBrush brush(Point(0, 0), Point(100, 100), color1, color2);REAL positions[] = {0.0f, 1.0f};
Color colors[] = {color1, color2};
brush.SetInterpolationColors(colors, positions, 2);// 定义正方形的位置和大小
RectF rectangle(100.0f, 100.0f, 100.0f, 100.0f);// 使用渐变画刷填充正方形
graphics.FillRectangle(&brush, rectangle);
在这个例子中,我们使用 FillRectangle 函数绘制了填充的正方形,并且使用 LinearGradientBrush 作为画刷的颜色。 Brush 的构造函数接受两个点,这里我们使用 Point(0, 0) 和 Point(100, 100) 定义了一个渐变的范围。
实现效果图
相关文章:

visual Studio MFC 绘制单一颜色三角形、渐变颜色边框三角形、渐变填充三角形、边框渐变的正方形与填充渐变的正方形实例
MFC 绘制三角形 本文使用visual Studio MFC 平台实现绘制单一颜色三角形、渐变颜色边框三角形、渐变填充三角形、边框渐变的正方形与填充渐变的正方形. 关于基础工程的创建请参考Visual Studio 使用MFC 单文档工程绘制单一颜色直线和绘制渐变颜色的直线 文章目录 MFC 绘制三角形…...

嵌入式八股 | 笔试面试 | 校招秋招 | 题目精选
嵌入式八股精华版1.0所有216道题目如下: 欢迎关注微信公众号【赛博二哈】并加入嵌入式求职交流群。提供简历模板、学习路线、岗位整理等 欢迎加入知识星球【嵌入式求职星球】获取完整嵌入式八股。 提供简历修改、项目推荐、求职规划答疑。另有各城市、公…...
)
力扣:180. 连续出现的数字(Python3)
题目: 表:Logs ---------------------- | Column Name | Type | ---------------------- | id | int | | num | varchar | ---------------------- 在 SQL 中,id 是该表的主键。 id 是一个自增列。 找出所有至少连续…...

【Python篇】详细讲解正则表达式
文章目录 🌹什么是正则表达式🍔语法字符类别重复次数组合模式 ✨例子 🌹什么是正则表达式 正则表达式(Regular Expression),简称为正则或正则表达式,是一种用于匹配、查找和操作文本字符串的工…...

Linux系统分区和挂载超过2T的硬盘
报错信息:DOS partition table format cannot be used on drives for volumes larger than 2199023255040 bytes for 512-byte sectors. Use GUID partition table format (GPT). 转载:Ubuntu(Linux)系统安装扩展硬盘并完成格式化及挂载 - 知乎...
Vue19 列表过滤
直接上代码 以下代码使用了两种实现方式,监视属性和计算属性 当能用计算属性实现时,推荐使用计算属性 <!DOCTYPE html> <html><head><meta charset"UTF-8" /><title>列表过滤</title><script type&q…...

【一起来学kubernetes】7、k8s中的ingress详解
引言配置示例负载均衡的实现负载均衡策略实现模式实现方案Nginx类型Ingress实现Treafik类型Ingress实现HAProxy类型ingress实现Istio类型ingress实现APISIX类型ingress实现 更多 引言 Ingress是Kubernetes集群中的一种资源类型,用于实现用域名的方式访问Kubernetes…...
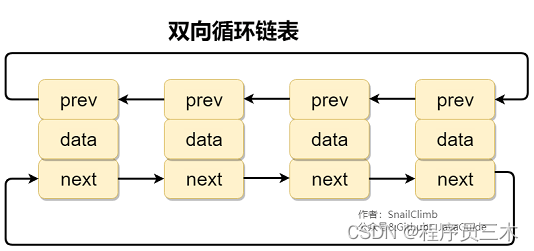
[Java] 阿里一面~说一下ArrayList 与 LinkedList 区别
文章目录 是否保证线程安全底层数据结构插入和删除是否受元素位置的影响是否支持快速随机访问内存空间占用: 是否保证线程安全 ArrayList 和 LinkedList 都是不同步的,也就是不保证线程安全; 底层数据结构 ● ArrayList 底层使用的是 Obje…...

凸包问题的GRAHAM-SCAN解法 open3d c++ 代码
使用了Open3D库进行点云处理和可视化。下面是代码的大致解释: 引入必要的头文件和命名空间: 定义了三个函数: ComputeTriangleDirArea:计算带符号三角形的面积。Compute2Ddistance:计算两点之间的平面距离。GetConvexHullByGrahamScan:通过Graham Scan方法计算凸包点集。…...
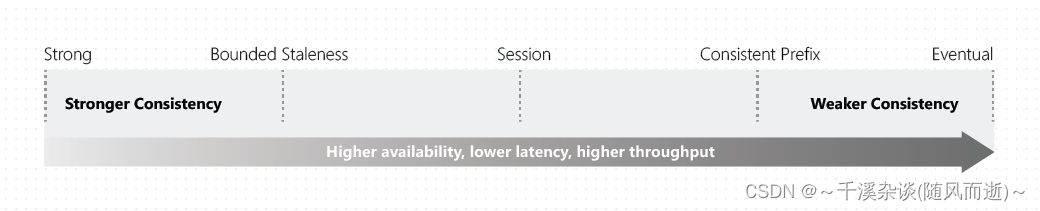
从微软Cosmos DB浅谈一致性模型
最近回顾了微软的Cosmos DB的提供一致性级别,重新整理下一致性模型的相关内容。 0. Cosmos DB Cosmos DB(Azure Cosmos DB)是由微软推出的一个支持多模型、多 API 的全球分布式数据库服务。它旨在提供高度可扩展性、低延迟、强一致性和全球…...
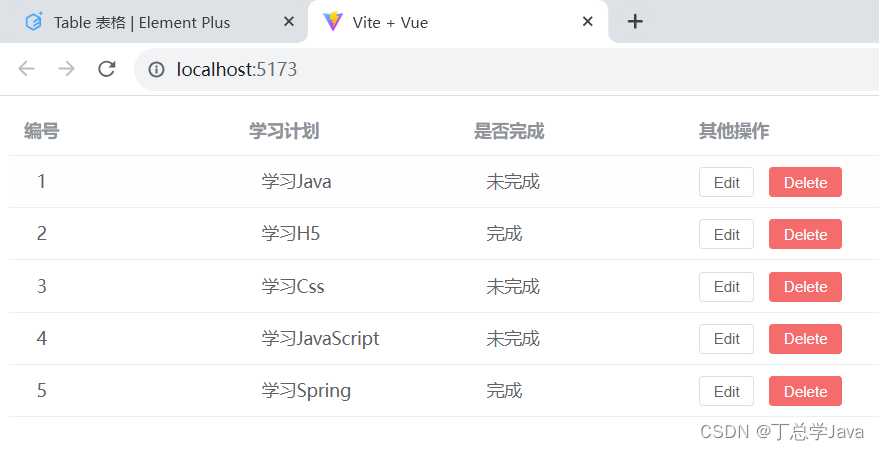
spring-webmvc练习-日程管理-访问后端展示列表数据
1、util/request.js import axios from "axios";let request axios.create({baseURL: "http://localhost:8080",timeout: 50000 });export default request 2、api/schedule.js import request from "../util/request.js";export let getSchedu…...

【Linux系统编程】操作系统详解(什么是操作系统?为什么会存在操作系统?设计操作系统的目的是什么?)
目录 一、前言 二、 什么是操作系统 💦操作系统的引入 💦操作系统的概念理解 💦操作系统设计的目的与定位 💦总结 二、操作系统之上之下分别有什么 三、深度理解操作系统的“管理” 💦场景理解 💦操…...

肖sir __数据库练习__001
建表语句: create table student ( id int(4),age int(8),sex int(4),name varchar(20), class int(4), math int(4)) DEFAULT charsetutf8; INSERT into student VALUES(1,25,1,‘zhansan’,1833,90); INSERT into student VALUES(2,25,1,‘lisi’,1833,67); INSER…...
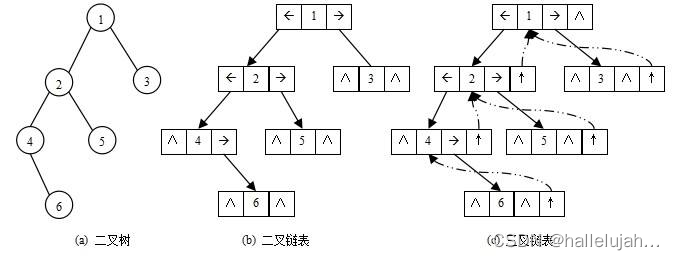
【数据结构初阶】树,二叉树
树,二叉树 1.树概念及结构1.1树的概念1.2 树的相关概念1.3 树的表示1.4 树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构2.1概念2.2现实中的二叉树2.3 特殊的二叉树2.4 二叉树的性质2.5 二叉树的存储结构 1.树概念及结构 1.…...

HTML新手入门笔记整理:HTML常用标签总结表
HTML常用标签 标签 英文全称 语义 div division 区块(块元素) span span 区块(行内元素) p paragraph 段落 ol ordered list 有序列表 ul unordered list 无序列表 li list item 列表项 dl definition list 定义列表 dt definition term 定义术语 d…...
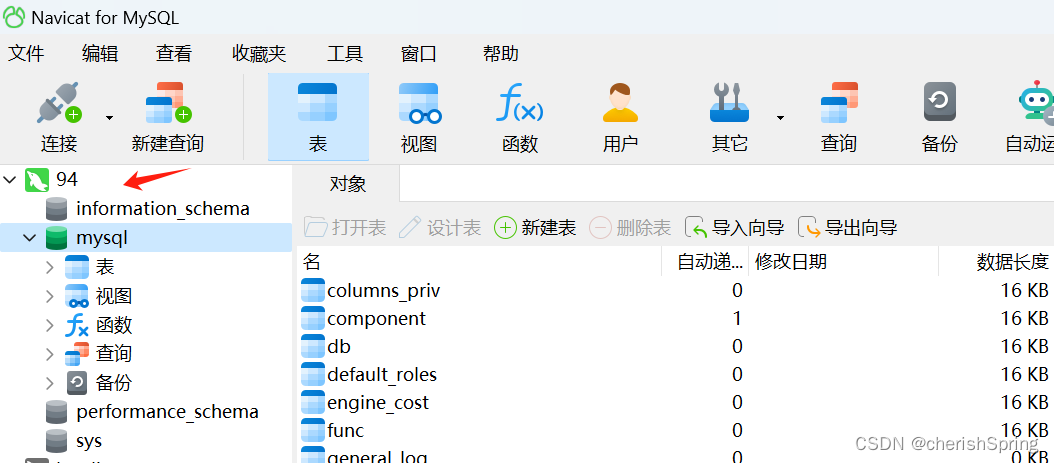
Linux7安装mysql数据库以及navicat远程连接mysql
1.下载地址:MySQL :: Download MySQL Community Server 2.创建mysql目录将压缩包上传到该目录 mkdir /opt/mysql cd /opt/mysql3.解压压缩包 gzip mysql-8.1.0-1.el7.x86_64.rpm-bundle.tar tar -zxvf mysql-8.1.0-1.el7.x86_64.rpm-bundle.tar.gz 4.前置检查 ch…...
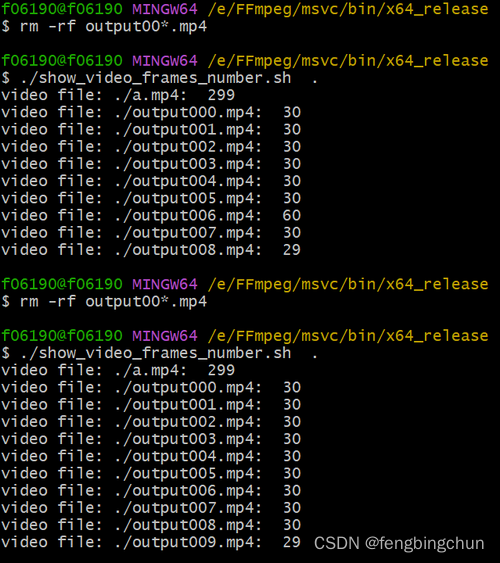
FFmpeg命令分隔视频
有一个视频如a.mp4,此视频采用帧率为30生成,共有299帧,这里通过FFmpeg命令分隔成1秒一个个的小视频,即每个小视频帧数为30帧。 用到的FFmpeg参数如下所示: (1).-i:指定输入视频文件的名称; (2).-c:指…...

开源与闭源
我的观点: 开源与闭源软件都有各自的优势和劣势,没有绝对的对错之分。.. 一、开源和闭源的优劣势比较 开源的好处与劣处 优势: 创新与合作:开源软件能够吸引更多的开发者参与到项目中来,促进创新和合作。开放的源代码…...

详解Python对Excel处理
Excel是一种常见的电子表格文件格式,广泛用于数据记录和处理。Python提供了多个第三方库,可以方便地对Excel文件进行读写、数据操作和处理。本文将介绍如何使用Python对Excel文件进行处理,并提供相应的代码示例和详细说明。 一、安装第三方库…...

docker compose搭建渗透测试vulstudy靶场示例
前言 渗透测试(Penetration test)即网络安全工程师/安全测试工程师/渗透测试工程师通过模拟黑客,在合法授权范围内,通过信息搜集、漏洞挖掘、权限提升等行为,对目标对象进行安全测试(或攻击)&am…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
