LeetCode 1250. Check If It Is a Good Array【数论】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
Given an array nums of positive integers. Your task is to select some subset of nums, multiply each element by an integer and add all these numbers. The array is said to be good if you can obtain a sum of 1 from the array by any possible subset and multiplicand.
Return True if the array is good otherwise return False.
Example 1:
Input: nums = [12,5,7,23] Output: true Explanation: Pick numbers 5 and 7. 5*3 + 7*(-2) = 1
Example 2:
Input: nums = [29,6,10] Output: true Explanation: Pick numbers 29, 6 and 10. 29*1 + 6*(-3) + 10*(-1) = 1
Example 3:
Input: nums = [3,6] Output: false
Constraints:
1 <= nums.length <= 10^51 <= nums[i] <= 10^9
题意:给出一个正整数数组 nums ,任务是选出 nums 的任一可能子集,将子集中每个元素乘以一个整数并求和,如果和为1,则说明 nums 是个好数组。
视角1 裴蜀定理
本题涉及数论中的裴蜀定理(具体证明可参考「裴蜀定理」百度百科),其内容为:对于不全为零的任意整数 a,ba, ba,b ,记 g=gcd(a,b)g=gcd(a,b)g=gcd(a,b) 为 a,ba,ba,b 的最大公约数,则对于任意整数 x,yx, yx,y 都满足 ax+byax + byax+by 是 ggg 的倍数,特别地存在整数 x,yx, yx,y 满足 ax+by=gax+by=gax+by=g 。这应该很好理解,ggg 为 a,ba,ba,b 最大公约数,则存在 m,nm,nm,n 满足 mg=a,ng=bmg =a,ng=bmg=a,ng=b ,所以对于任意整数 x,yx,yx,y 都有 ax+by=g(mx+ny)ax+by=g(mx+ny)ax+by=g(mx+ny) 是 ggg 的倍数。
推广到多个整数的情况:对于不全为零的任意整数 a1,a2,…,ana_1,a_2,\dots,a_na1,a2,…,an ,记 ggg 为这 nnn 个数的最大公约数,则对于任意 nnn 整数 x1,x2,…,xnx_1,x_2,\dots,x_nx1,x2,…,xn 都满足 a1x1+⋯+anxna_1x_1+\dots + a_nx_na1x1+⋯+anxn 是 ggg 的倍数,特别地存在整数 x1,…,xnx_1,\dots, x_nx1,…,xn 满足 a1x1+⋯+anxn=ga_1x_1+\dots +a_nx_n=ga1x1+⋯+anxn=g 。
一个重要推论是:正整数 a1,…,ana_1,\dots,a_na1,…,an 的最大公约数是 111(充分必要条件)⇔\Leftrightarrow⇔ 存在 nnn 个整数 x1,…,xnx_1,\dots,x_nx1,…,xn 满足 a1x1+⋯+anxn=1a_1x_1+\dots+a_nx_n =1a1x1+⋯+anxn=1 。
视角2 辗转相减法
求两个数的最大公因数,可以使用辗转相减法。回忆下述递归过程,不难发现:这一过程压缩后等价于,两个数 a,ba, ba,b 通过同时乘以两个特定整数,再求和可得它们的最大公因数。因此,如果它们的最大公因数为1,则说明存在两个特定整数 x,yx,yx,y 使得 ax+by=1ax+by=1ax+by=1 。反过来说,如果存在两个特定整数 x,yx,yx,y 使得 ax+by=1ax+by=1ax+by=1 ,则 gcd(a,b)=1gcd(a,b)=1gcd(a,b)=1(说明 a,ba,ba,b 通过辗转相减可得1,即 a,ba,ba,b 最大公因数为1)。
int gcd(a, b) {if (a > b) swap(a, b); // 使得a<=bif (a == 0) return b; // 如果a为0,则gcd(0,b)=breturn gcd(a, b - xa); // x是使得xa最大、但xa<=b的某一正整数// b-xa其实就是b%a
}
从而,如果一个互质数组的最大公因数是1,那就一定存在一组整数可以让它们相乘求和得到1。反过来说也可行。
对于 nums 来说,如果存在一个数组子集满足题意(即存在一组整数使它们互乘再求和为1),则说明该数组子集是互质的,从而 nums 一定是互质的。如果 nums 不是互质的,则 nums 就不是好数组。
其他视角
从一些简单的例子入手来思考本题。示例三给的 nums = [3, 6] ,可以先朴素地列出所有的可能性,其子集为 {}, {3}, {6}, {3, 6} 。
- 空集显然不符合要求。
{3}, {6}显然也不符合要求。因为对于任意不为1的正整数 xxx ,乘以任意整数 aaa 的结果 axaxax 都不可能为1。当且仅当 x=1x=1x=1 时,才存在唯一的整数 a=1a=1a=1 能使 axaxax 满足 ax=1ax = 1ax=1 。{3, 6}也不符合要求。假设 yyy 和 zzz 是任意整数,我们需要找到使得 3y+6z=13y+6z=13y+6z=1 的那对 (y,z)(y, z)(y,z) 。由于 3y+6z=3(y+2z)3y+6z=3(y+2z)3y+6z=3(y+2z) ,而 (y+2z)(y + 2z)(y+2z) 可看作是一个整体的整数,由上一点的分析可知,不存在这样的整数 a=(y+2z)a = (y + 2z)a=(y+2z) 使得 3a=13a = 13a=1 。3是3和6的最大公约数,因此可以大胆猜测最大公约数应在本题中占很重要的位置。
因此对两个正整数 a,ba, ba,b ,假设其最大公约数为 ggg 使得 a=mg,b=nga=mg, b=nga=mg,b=ng ,考虑任意整数 x,yx,yx,y ,则 ax+by=g(mx+ny)ax + by=g(mx + ny)ax+by=g(mx+ny) ,可知 mx+nymx+nymx+ny 必定是整数,如要找到某一对 x,yx,yx,y 使得 g(mx+ny)=1g(mx+ny)=1g(mx+ny)=1 成立,则唯一的可能性是 g=1g=1g=1 且 (mx+ny)=1(mx+ny)=1(mx+ny)=1 。也就是 a,ba,ba,b 的最大公因数必须是1。
解法 数论
由裴蜀定理可得,题意等价于:如果 nums 中全部整数的最大公约数为1(即为互质数组),则 nums 为好数组。否则不是。
class Solution:def isGoodArray(self, nums: List[int]) -> bool:return reduce(gcd, nums) == 1
相关文章:

LeetCode 1250. Check If It Is a Good Array【数论】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

ETHDenver 2023
ETHDenver是全球最大、持续时间最长的以太坊活动之一,今年的活动定于2月24日至3月5日在美国科罗拉多州丹佛市盛大举行。这次活动将面向以太坊和其他区块链协议爱好者、设计者和开发人员。Moonbeam作为ETHDenver 2023的Meta赞助商,将在本次活动中展示令人…...

React架构演变
老版React架构 React 16之前的架构 其实就分为两个部分: Reconciler协调器Render渲染器 Reconciler协调器负责本次更新有什么组件需要被渲染,diff算法就发生在这个步骤中,在diff算法中会将上次更新的组件和本次更新的组件做一个对比&…...
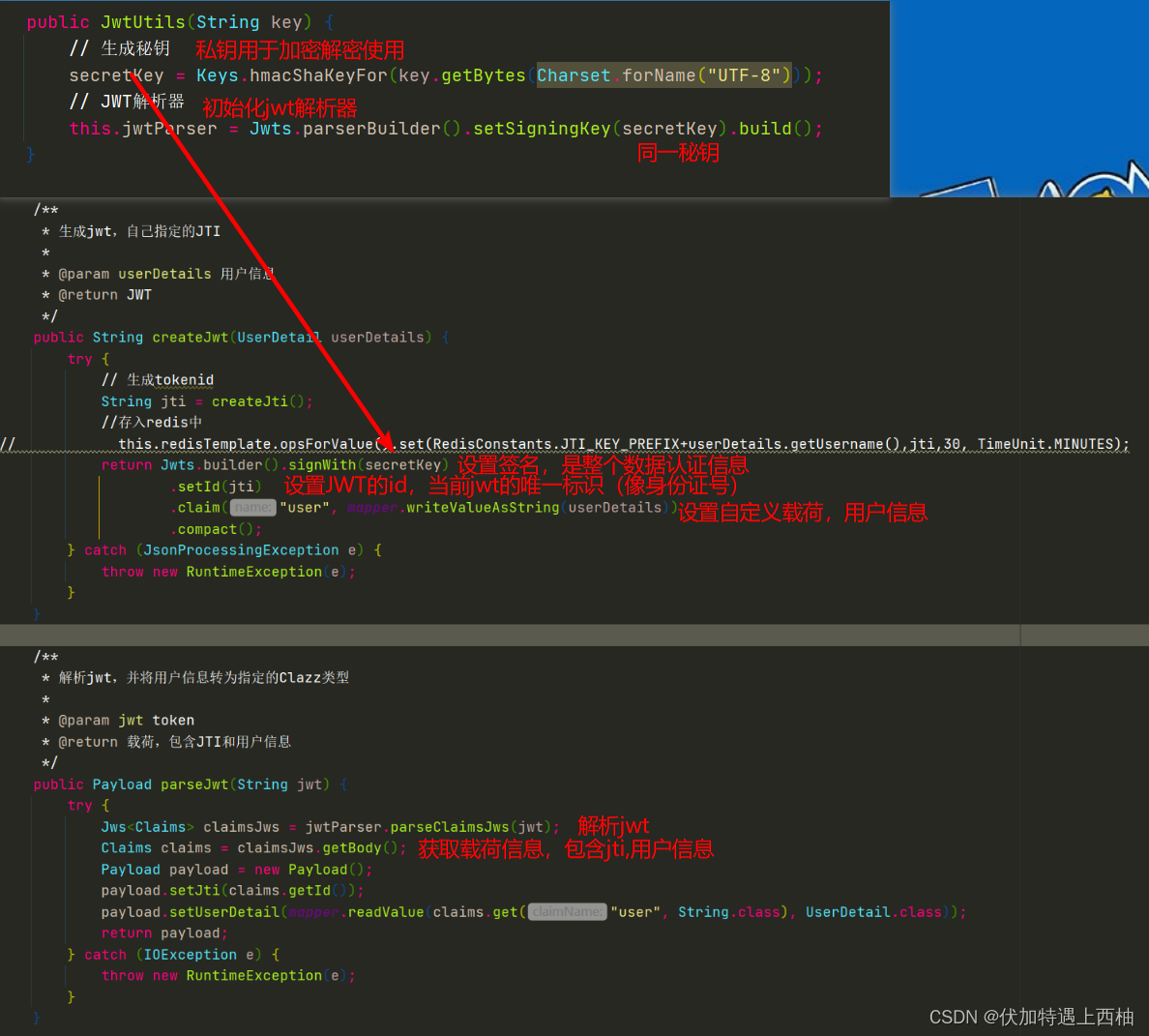
安全认证--JWT介绍及使用
安全认证--JWT介绍及使用1.无状态登录原理1.1.什么是有状态?1.2.什么是无状态1.3.如何实现无状态1.4.JWT1.4.1.简介1.4.2.数据格式2.编写JWT工具2.1.添加JWT依赖2.2.载荷对象2.3.工具2.4.测试2.4.1.配置秘钥2.4.2.测试类1.无状态登录原理 有状态登录和无状态登录详…...
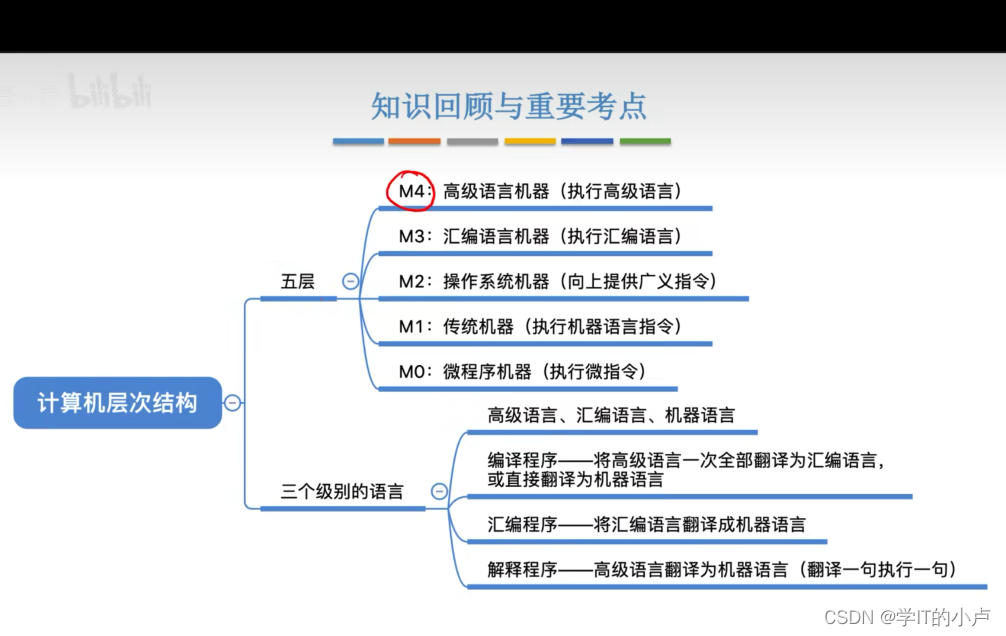
【计算机组成原理】计算机硬件的基础组成、认识各个硬件部件
计算机组成原理(一) 计算机内部是通过电信号传递数据 电信号:分为高电平和低电平,分别代表1/0 数字、文字、图像如何用二进制表示? CPU如何对二进制数进行加减乘除? 如何存储这些二进制数的? 如何从内存中取出想要的数…...

使用ChIPSeeker进行ChIP-seq, ATAC-seq,cuttag等富集峰的基因组注释
二代测序产生的数据类型 常规的下一代高通量测序(next generation sequencing, NGS)实验通常产生大量短片段(reads),通常我们需要将这些reads比对到参考基因组/转录组上,即将它们置于生物学上有意义的基因背景下,才能…...
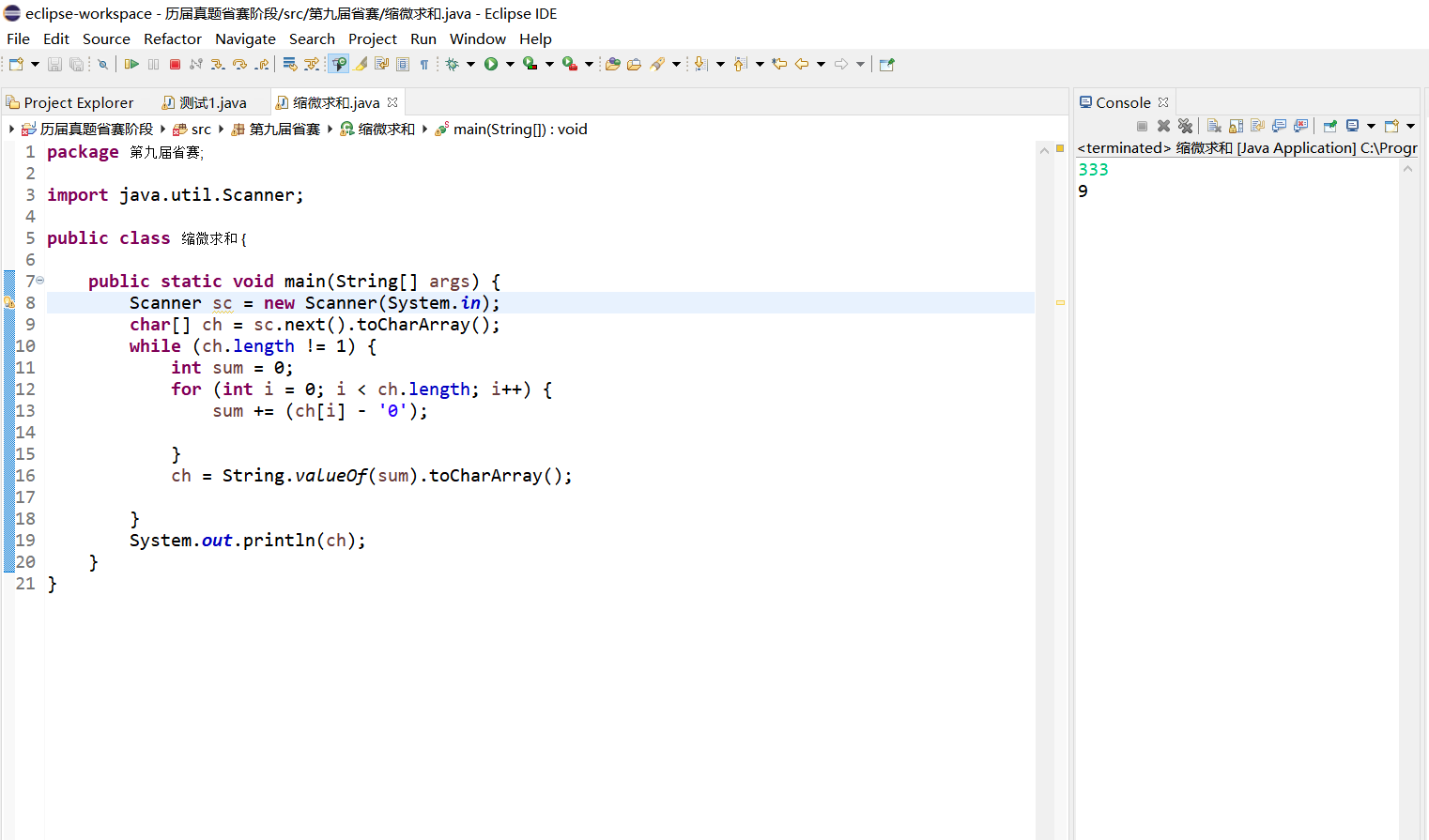
第九届蓝桥杯省赛——7缩位求和
题目:在电子计算机普及以前,人们经常用一个粗略的方法来验算四则运算是否正确。比如:248 * 15 3720把乘数和被乘数分别逐位求和,如果是多位数再逐位求和,直到是1位数,得2 4 8 14 > 1 4 5;1 5 65…...

【c++】STL常用容器5—list容器
文章目录list基本概念list构造函数list赋值和交换list大小操作list插入和删除list数据存取list反转和排序list基本概念 功能:将数据进行链式存储。 链表(list)是一种物理存储单元上非连续的存储结构,数据元素的逻辑顺序是通过链…...

【牛客刷题专栏】0x0D:JZ5 替换空格(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...

聚观早报 | 苹果2024年放弃高通;腾讯回应进军类 ChatGPT
今日要闻:苹果2024年放弃高通;腾讯回应进军类 ChatGPT;小米发布无线AR眼镜探索版;50%的美国企业已在使用ChatGPT;Snap推出ChatGPT驱动的聊天机器人 苹果2024年放弃高通 高通公司 CEO 兼总裁克里斯蒂亚诺・安蒙…...
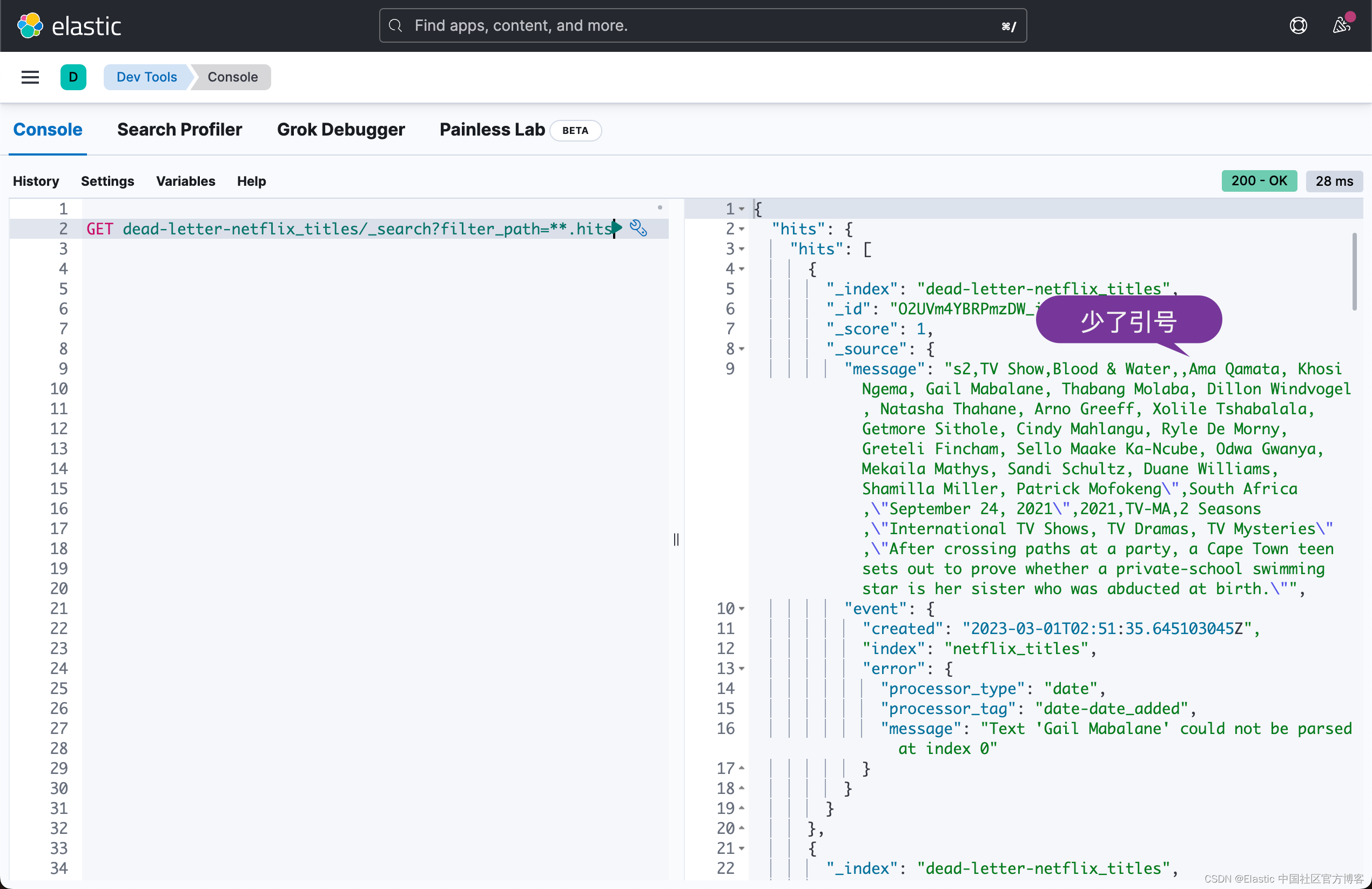
Elasticsearch:如何正确处理 Elasticsearch 摄取管道故障
在我之前的文章 “Elastic:开发者上手指南” 中的 “Ingest pipeline” 章节中个,我有很多文章是关于 ingest pipeline 的。在今天的文章中,我将重点介绍如何处理在摄取管道中的错误。在我之前的文章 “Elasticsearch:如何处理 in…...
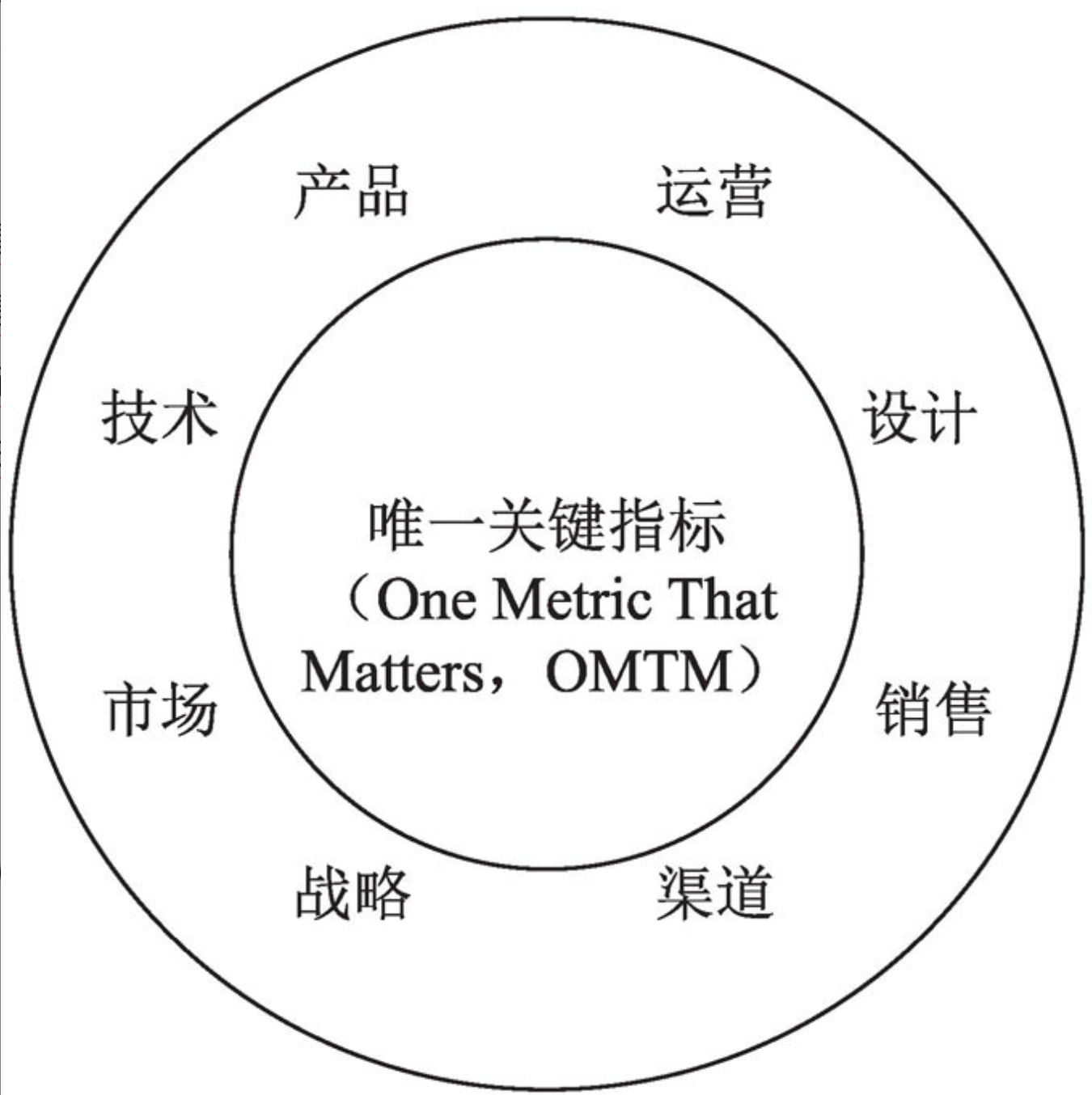
指标体系—北极星指标体系
北极星指标体系 每个产品都有很多指标,每个指标都反映了对应业务的经营情况。但是在实际业务经营中,却要求我们在不同的产品阶段寻找到合适的指标,让这个指标可以代表当前产品阶段的方向和目标,让这个指标不仅对业务经营团队,而且对产品的用户、对产品的价值都能有很好的…...
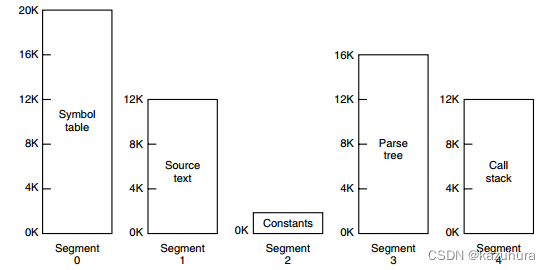
【操作系统】内存管理
虚拟内存 虚拟内存的目的是为了让物理内存扩充成更大的逻辑内存,从而让程序获得更多的可用内存。 为了更好的管理内存,操作系统将内存抽象成地址空间。每个程序拥有自己的地址空间,这个地址空间被分割成多个块,每一块称为一页。…...
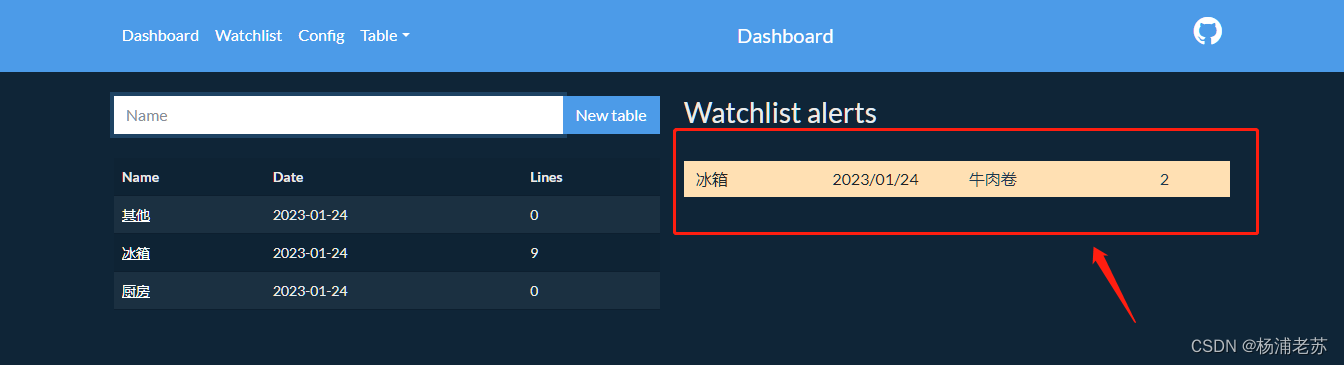
家庭消耗品跟踪管理软件HomeLists
什么是 HomeLists ? HomeLists 是一款自托管耗材统计软件,能通过提醒等帮助您跟踪家庭消耗品。 安装 在群晖上以 Docker 方式安装。 在注册表中搜索 homelists ,选择第一个 aceberg/homelists,版本选择 latest。 本文写作时&…...
)
django模型简要(1)
1. AbstractUser(内置用户模型类)的使用 ### 需要在settings.py中添加如下: AUTH_USER_MODEL app.MyUser 说明:这是为了覆盖django默认的User model;app即模型所属app,MyUser即AbstractUser实现类。 2.on_delete选项 从django3.…...

【shell 编程大全】sed详解
sed详解1. 概述 今天单独拉出一章来讲述下sed命令。因为sed命令确实内容太多,不过也是比较灵活的,好了不废话了。我们开始吧 1.2 原理解析 shell脚本虽然功能很多,但是它最常用的功能还是处理文本文件,尤其是在正常的业务操作流程…...
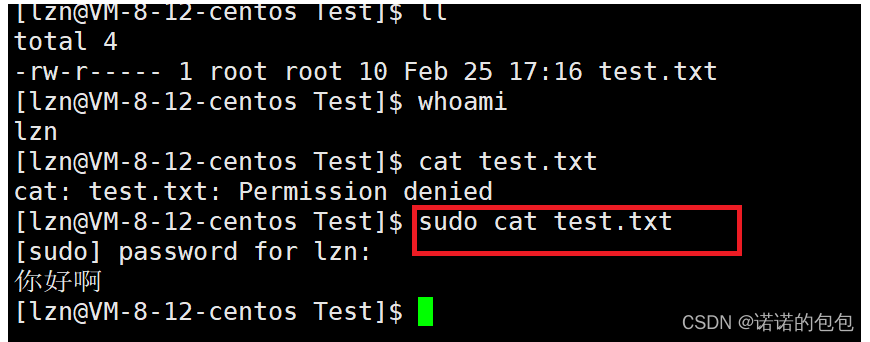
关于sudo配置
前言这里做一个小补充,主要讲一下关于利用sudo对指令提权以及普通用户无法使用sudo指令的问题。在前面的文章【Linux】一文掌握Linux权限中,我们讲到了关于权限的一些问题。我们知道root身份下,一切畅通无阻,而权限只是用来限制我…...
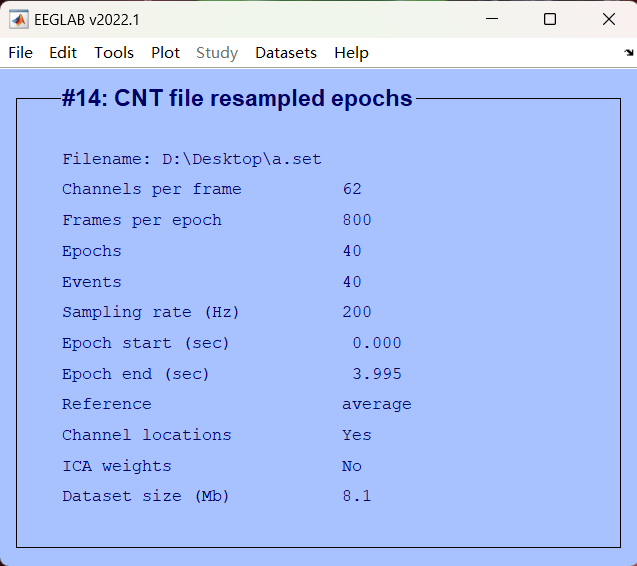
EEGLAB处理运动想象脑电数据
最近在看论文时,经常看到作者处理数据的过程,之前都是一代而过,知道怎么处理就可以了,一直没有实践,最近需要一些特殊的数据,需要自己处理出来,这里尝试着自己用MATLAB处理数据,记录…...

span标签的使用场景
目录 前言 一、span标签是什么? 二、span常用 1.可以嵌套a标签。 2.直接使用 3.加样式使用 4.加按钮使用 5.加a标签的综合使用 6.跟table结合使用 总结 前言 本篇章主要记录一下开发日常中,所常遇见的使用span标签的场景。 一、span标签是什么…...
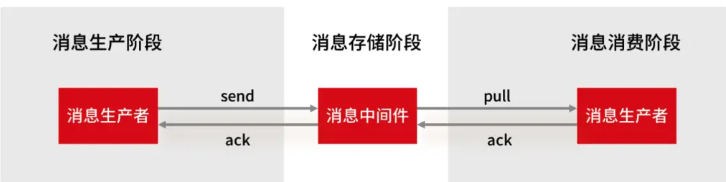
Kafka面试问题总结
kafka架构2.基础概念Producer(生产者) : 产生消息的一方。Consumer(消费者) : 消费消息的一方。Broker(代理) : 可以看作是一个独立的 Kafka 实例。多个 Kafka Broker 组成一个 Kafka Cluster。同时&#x…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
