支持向量机的算法原理
支持向量机(Support Vector Machine,简称SVM)是机器学习领域中一种常用的分类算法,它基于统计学习理论和结构风险最小化原则,具有很强的理论基础和良好的分类性能。本文将详细介绍支持向量机的算法原理,并解释SVM为什么能够有效地处理线性可分和线性不可分问题。同时,我们将通过一个具体的案例来演示支持向量机的应用过程。
一、支持向量机的基本概念和目标
支持向量机的基本概念是在特征空间中找到一个超平面来划分不同类别的样本。超平面是一个(d-1)维的子空间,其中d是特征空间的维数。SVM的目标是找到一个最优的超平面,使得该超平面能够最大化不同类别之间的间隔。这个最优的超平面被称为最大间隔超平面。
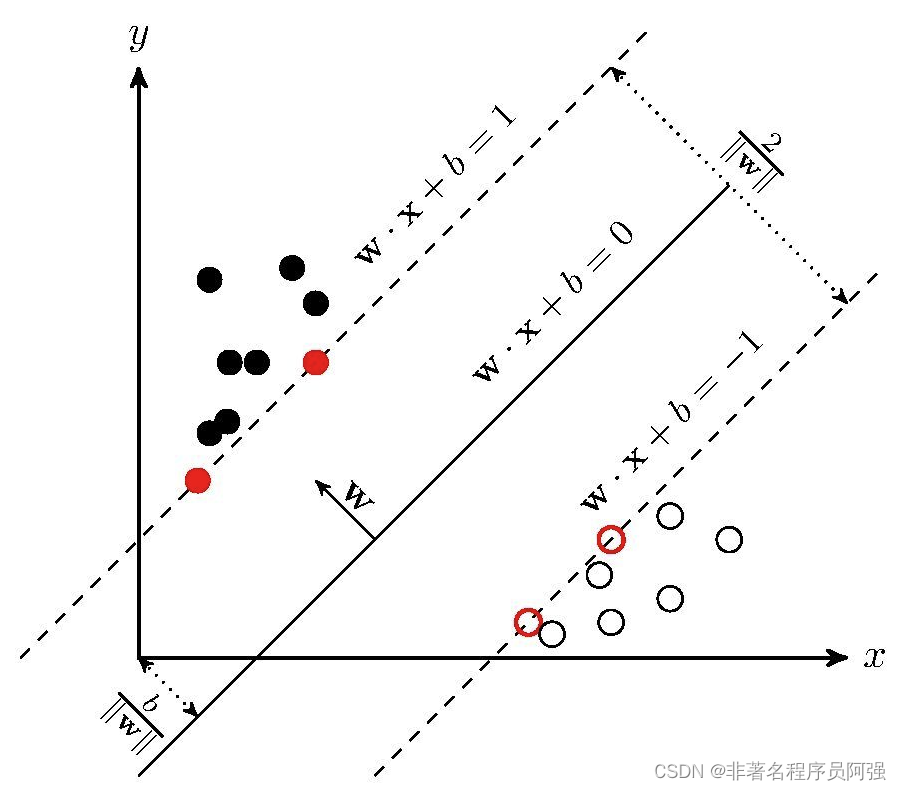
二、线性可分支持向量机的算法原理
当样本集线性可分时,SVM的主要思想是利用支持向量来确定最大间隔超平面。支持向量是离超平面最近的一些样本点。这些样本点位于间隔边界上,可以提供决策函数的间隔值。
SVM的目标是最大化间隔,这等价于最小化目标函数,即结构风险。结构风险最小化准则可以表示为:
minimize 1/2 * ||w||^2
subject to y_i*(w*x_i+b) >= 1, i=1,2,...,N
其中,x_i表示样本特征向量,y_i表示样本类别,w是超平面的法向量,b是超平面的截距。
由于目标函数是一个凸二次规划问题,可以通过求解对偶问题来得到最优解。通过求解对偶问题,我们可以得到优化问题的解,即超平面的法向量w和截距b。通过求解拉格朗日函数,我们可以得到对偶问题的优化目标。
三、线性不可分支持向量机的算法原理
在现实问题中,很多样本集并不是线性可分的,这时我们可以使用核函数来将低维特征空间映射到高维特征空间中。利用核函数,我们可以将线性不可分的问题转化为线性可分的问题。
核函数是一种间接计算高维特征空间内积的方法。常见的核函数包括线性核、多项式核、高斯核等。SVM的基本原理是寻找一个在特征空间中线性可分的超平面,然后将其映射回原始样本空间。

四、支持向量机的应用案例
接下来,我们将通过一个具体的案例来演示支持向量机的应用过程。假设我们有一个二维空间中的样本集,其中包含两个类别的样本点。我们的目标是找到一个超平面,将两个类别的样本点正确分类。
我们首先加载数据集,然后对数据进行预处理和特征工程。接着,我们构建一个支持向量机模型,并选择适当的核函数。然后,我们使用训练集对模型进行训练。最后,我们使用测试集进行预测,并评估模型的性能。
通过上述案例的应用,我们可以看到支持向量机在解决分类问题上具有很好的性能。无论是线性可分还是线性不可分的问题,SVM都能够通过找到合适的超平面来完成分类任务。
结论:
本文详细介绍了支持向量机的算法原理,并解释了SVM为什么能够有效地处理线性可分和线性不可分问题。无论是线性可分还是线性不可分的问题,SVM通过最大化间隔或利用核函数映射特征空间,都能够找到一个合适的超平面来进行分类。通过一个具体的案例,我们演示了支持向量机的应用过程。希望本文能够对您了解支持向量机的算法原理有所帮助。谢谢阅读!
人工智能的学习之路非常漫长,不少人因为学习路线不对或者学习内容不够专业而举步难行。不过别担心,我为大家整理了一份600多G的学习资源,基本上涵盖了人工智能学习的所有内容。点击下方链接,0元进群领取学习资源,让你的学习之路更加顺畅!记得点赞、关注、收藏、转发哦!扫码进群领资料
相关文章:

支持向量机的算法原理
支持向量机(Support Vector Machine,简称SVM)是机器学习领域中一种常用的分类算法,它基于统计学习理论和结构风险最小化原则,具有很强的理论基础和良好的分类性能。本文将详细介绍支持向量机的算法原理,并解…...
)
gitlab 12升级14(解决各种报错问题)
1.这里是从自己公司的源下载的rpm包,需要换成自己的 2.从12的最后一个版本升级到14的最后一个版本 # 停服务 [rootdocker test]# gitlab-ctl stop puma && gitlab-ctl stop sidekiq && gitlab-ctl stop nginx && gitlab-ctl status# 进入…...

给element plus中动态form-item增加校验的可行方法
element plus中的form组件自带校验机制。在常规使用场景中,表单项是固定的、明确的,且数量不会太多。校验规则的使用也如下: <template><div class"edit-page"><el-form :model"formModel" ref"for…...

C++学习之值传递
c/c中存在三种传值方式,在局部函数中,对这三种传值方式传入的参数进行修改,会得到不同的结果。具体见下例: #include <stdlib.h> #include <stdio.h>static int dummny 10000;// 传值(传过来的是原始值的副本&#…...

网络视频播放卡顿原因分析
一、问题描述 某项目通过拉摄像机rtsp流转rtmp/http-flv/ws-flv的方案,使用户可以在网页中观看摄像机的视频画面。在 观看视频时偶发出现卡顿现象。 二、卡顿现象分析和解决 此问题涉及的原因较多,所以得考虑各环节的问题可能性,并根据现场实…...

Android 相机库CameraView源码解析 (二) : 拍照
1. 前言 这段时间,在使用 natario1/CameraView 来实现带滤镜的预览、拍照、录像功能。 由于CameraView封装的比较到位,在项目前期,的确为我们节省了不少时间。 但随着项目持续深入,对于CameraView的使用进入深水区,逐…...
计算机缺少d3dx9_43.dll怎么办?5个方法快速修复d3dx9_43.dll文件
在计算机使用过程中,我们常常会遇到一些错误提示,其中之一就是“d3dx9_43.dll丢失”。这个问题可能会影响到我们的游戏体验或者软件运行。为了解决这个问题,我查阅了一些资料并尝试了多种方法。在这里,我想分享一下我对d3dx9_43.d…...
2023亚太杯数学建模C题思路分析 - 我国新能源电动汽车的发展趋势
1 赛题 问题C 我国新能源电动汽车的发展趋势 新能源汽车是指以先进技术原理、新技术、新结构的非常规汽车燃料为动力来源( 非常规汽车燃料指汽油、柴油以外的燃料),将先进技术进行汽车动力控制和驱动相结 合的汽车。新能源汽车主要包括四种类型&#x…...

c语言新龟兔赛跑
以下是一个使用C语言编写的新的龟兔赛跑游戏: #include <stdio.h>#include <stdlib.h>#include <time.h>int main() { int distance, turtle_speed, rabbit_speed, turtle_time, rabbit_time, rabbit_lead; srand(time(NULL)); // 随机数种…...
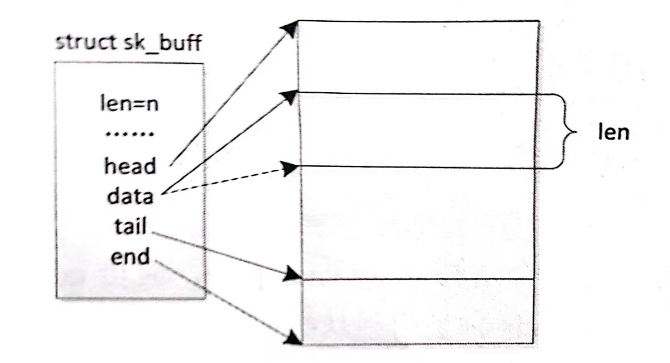
Linux驱动开发——网络设备驱动(理论篇)
目录 一、前言 二、网络层次结构 三、网络设备驱动核心数据结构和函数 一、前言 网络设备驱动是 Linux 的第三大类驱动,也是我们学习的最后一类 Linux 驱动。这里我们首先简单学习一下网络协议层次结构,然后简单讨论 Linux 内核中网络实现的层次结构。…...

simulink仿真
1)系统问题 连续系统,离散系统(采样周期问题) 系统分析问题 2)求解器问题 变步长,定步长,步长时间与采样周期问题、 3)积分器问题 连续积分,离散积分问题ÿ…...
PC端页面进去先出现加载效果
自定义指令v-loading,只需要绑定Boolean即可 v-loading“loading” <el-table :data"list" border style"width: 100%" v-loading"loading"><el-table-column align"center" label"序号" width"5…...
磁盘清理在哪里?学会这4个方法,快速清理内存!
“在使用电脑的过程中,我可能经常会保存一些文件到电脑上,这也导致电脑经常出现内存不足的情况。我想问问磁盘清理在哪里呀?我应该如何打开呢?” 随着使用电脑的时间增长,用户可能经常会遇到磁盘空间不足的情况&#x…...
Error opening terminal: xterm.”的解决方法
主要是看下面这两个变量是否设置正确 $ echo $TERM $ echo $TERMINFO 通常TERM的默认值为xterm-265color, 要查看支持的term,可以ls -al /lib/terminfo/x/ 如果TERM是xterm-265color的话,TERMINFO设置为/usr/lib/terminfo make menuconfig时提示“Err…...

C#常见的设计模式-结构型模式
引言 设计模式是软件工程中用于解决常见问题的可复用解决方案。在C#编程中,常见的设计模式具有广泛的应用。本篇博客将重点介绍C#中常见的结构型设计模式,包括适配器模式、装饰器模式、代理模式、组合模式和享元模式。 目录 引言1. 适配器模式(Adapter …...

Redis分片备库切换操作
Redis分片备库切换操作 场景描述: 分片集群: 1.ipa:5001-ipa:5002 2.ipb:5001-ipb:5002 需将两个分片备库互置完成灾备 操作步骤 准备工作 主机密码:1qaz!QAZ 获取节点信息命令 /redispath/bin/redis-cli -a password -h ip -p port red…...
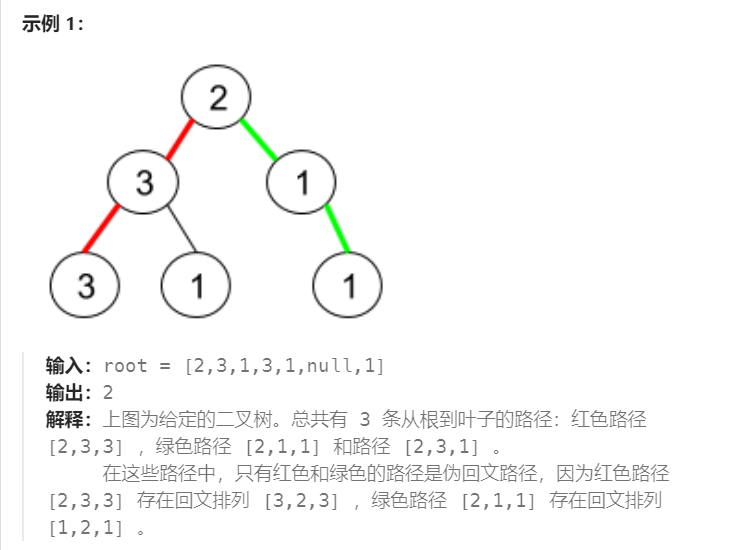
二叉树:leetcode1457. 二叉树中的伪回文路径
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。 请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。 给定二叉树的节点数目…...
【【Linux下的Petallinux 以及其他的配置】】
Linux下的Petallinux 以及其他的配置 sudo apt-get install iproute2 gawk python3 python build-essential gcc git make net-tools libncurses5-dev tftpd zlib1g-dev libssl-dev flex bison libselinux1 gnupg wget git-core diffstat chrpath socat xterm autoconf libtoo…...

13、深度学习之神经网络
深度学习是机器学习中重要的一个学科分支,它的特点就在于需要构建多层“深度”的神经网络。 人们在探索人工智能初期,就曾设想构建一个用数学方式来表达的模型,它可以模拟人的大脑,大脑我们都知道,有很多神经元,每个神经元之间通过突触链接。 神经网络的设计就是模仿了这…...

js的数组去重方法
目录 es6数组中对象去重 1. filter()用法 2. findIndex()用法 3. 去重 其他方法: 方法二:reduce()去重 1. reduce()用法 1.1 找出字符长度最长的数组成员。 1.2 扁平化二维数组 1.3 扁平化多维数组 三、总结方案: 使用Set…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
