当前位置： 首页 > news >正文

【数据结构】二叉树概念 | 满二叉树 | 完全二叉树

news 2026/2/9 15:01:58

二叉树的概念

二叉树在实践中用的很多。

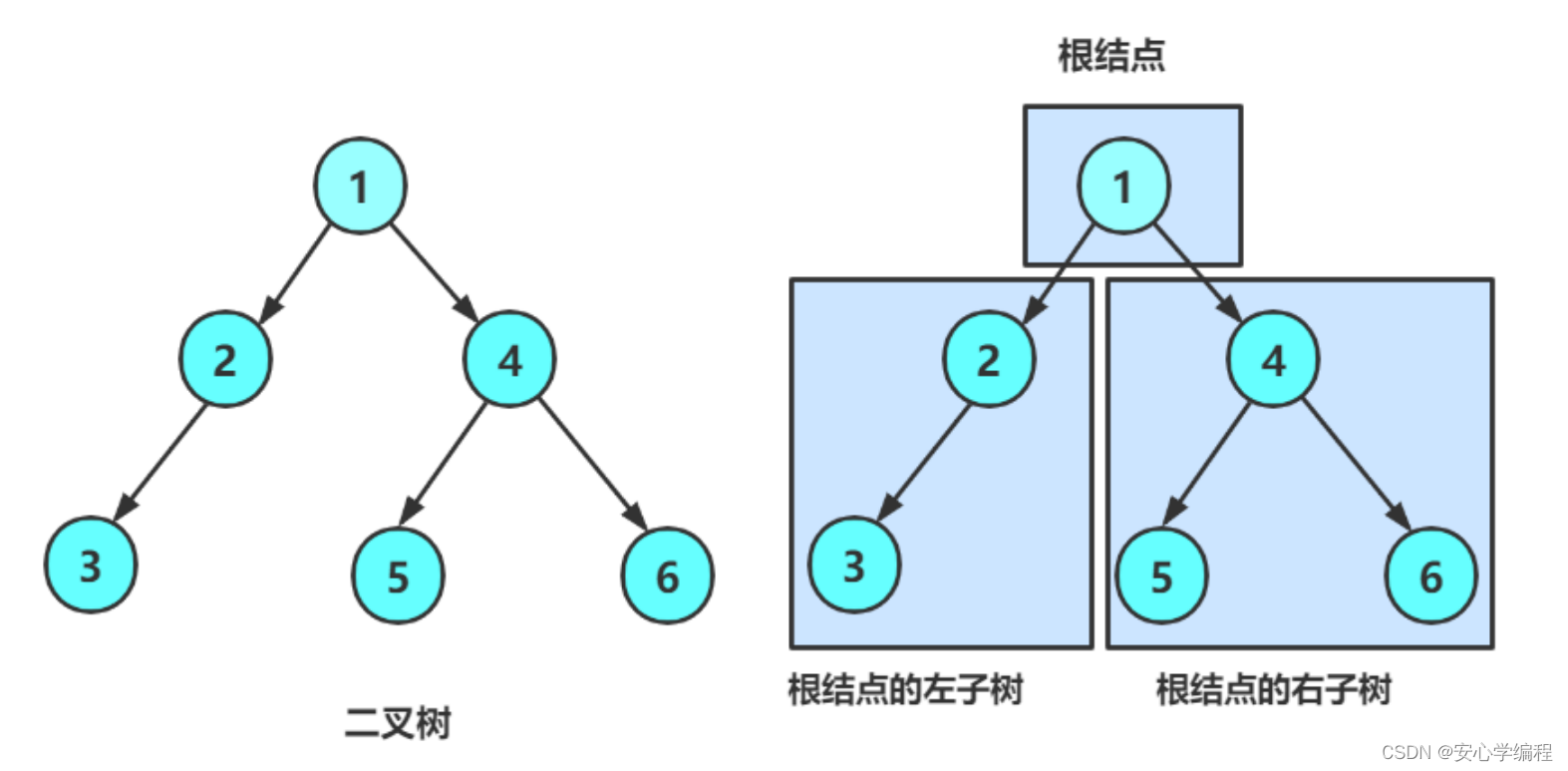
一棵二叉树是结点的一个有限集合，该集合：

  • 或者为空；
  • 由一个根结点加上两棵别称为左子树和右子树的二叉树组成。
  • 二叉树最多两个孩子。

这里注意：二叉树并不是度为2的树。

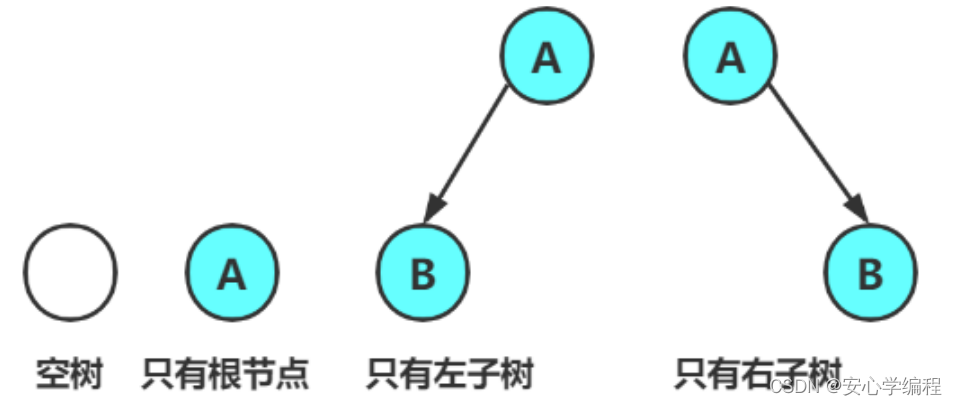
二叉树的度最大值是2，并不是说它的度一定为2。所以一下这四种情况也均是二叉树：

  • 空树
  • 只有根节点
  • 只有左子树
  • 只有右子树
  • 左右子树均存在

二叉树不存在度大于2的节点；

二叉树的子树有左右之分，次序是不能颠倒的，因此二叉树是有序树。

二叉树通俗也可以理解为对树进行了“计划生育”。 “计划生育”也就是生两个小孩，但是是每一家来说都是生两个吗？

那么度为2的一定是二叉树吗？

  • 度为2一定是二叉树。度为2的话，那么所有节点的最大的度就是2，而二叉树的概念是不存在度大于2的节点。
  • 二叉树是一个特殊的树，它的度最大为2，但是并没有说一定为2。

特殊的二叉树

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，那么这个二叉树就是满二叉树。也就是说，如果一个二叉树的成熟为K，那么结点总数就是2^{K}-1，那么它就是满二叉树。

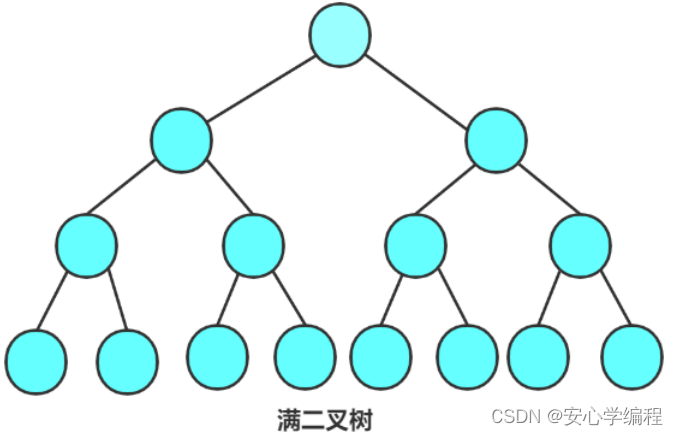
根据上图：

  • 假设高度为h，那么就会有2^{h}-1的节点；
  • 那么假设树有N个节点的话，那就是 2^{h}-1=N；那么 高度就为 h=\log _{2}(N+1)。

完全二叉树

完全二叉树，前h-1层都是满的，最后一层不一定满，但是从左到右必须连续。

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深入为K的，有n个节点的二叉树，当且仅当其每一个节点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

这里注意二叉树顺序是固定的，必须是连续的。

假设完全二叉树的高度为h，那么它的结点数量是多少呢？

完全二叉树的最后一层的范围： \left [ 2^{h-1},2^{h}-1 \right ]

思路：

  • 这里我们想在满二叉树中，结点数为2^{h}-1；
  • 那么满二叉树中的上一层就是有2^{h-1}-1；
  • 因为完全二叉树就是满二叉树的基础上，最后一层不满，也就是最后一层的结点数最多有2^{h-1}，最少有1个；
  • 所以根据等比公式可以求得出完全二叉树最后一层的范围为： \left [ 2^{h-1} , 2^{h}-1 \right ]。

相关文章：

【数据结构】二叉树概念 | 满二叉树 | 完全二叉树

二叉树的概念 二叉树在实践中用的很多。 一棵二叉树是结点的一个有限集合，该集合： 或者为空；由一个根结点加上两棵别称为左子树和右子树的二叉树组成。二叉树最多两个孩子。 这里注意：二叉树并不是度为2的树。 二叉树的度最大值是…...

编程日记 2023/11/28 0:07:35

第 373 场 LeetCode 周赛题解

A 循环移位后的矩阵相似检查 模拟 class Solution { public:bool areSimilar(vector<vector<int>> &mat, int k) {int m mat.size(), n mat[0].size();k % n;auto g mat;for (int i 0; i < m; i)if (i & 1)rotate(mat[i].begin(), mat[i].begin() …...

编程日记 2023/11/28 0:06:33

C#，《小白学程序》第二十五课：大数乘法（BigInteger Multiply）的Karatsuba算法及源代码

1 文本格式 /// <summary> /// 《小白学程序》第二十五课&#xff1a;大数&#xff08;BigInteger&#xff09;的Karatsuba乘法 /// Multiplies two bit strings X and Y and returns result as long integer /// </summary> /// <param name"a">&…...

编程日记 2023/11/28 0:05:32

Redis的五大数据类型详细用法

我们说 Redis 相对于 Memcache 等其他的缓存产品&#xff0c;有一个比较明显的优势就是 Redis 不仅仅支持简单的key-value类型的数据&#xff0c;同时还提供list&#xff0c;set&#xff0c;zset&#xff0c;hash等数据结构的存储。本篇博客我们就将介绍这些数据类型的详细使用…...

编程日记 2023/11/28 0:04:30

C++类与对象(6)—初始化列表、explicit关键字、static成员

目录 一、初始化列表 1、定义 2、注意事项 3、尽量使用初始化列表初始化 4、初始化顺序 二、 explicit关键字 1、定义 2、特点 三、static成员 1、定义 2、特性 3、例题 一、初始化列表 下面这段代码可以正常编译&#xff1a; class A { private:int _a1;//成员…...

编程日记 2023/11/28 0:03:29

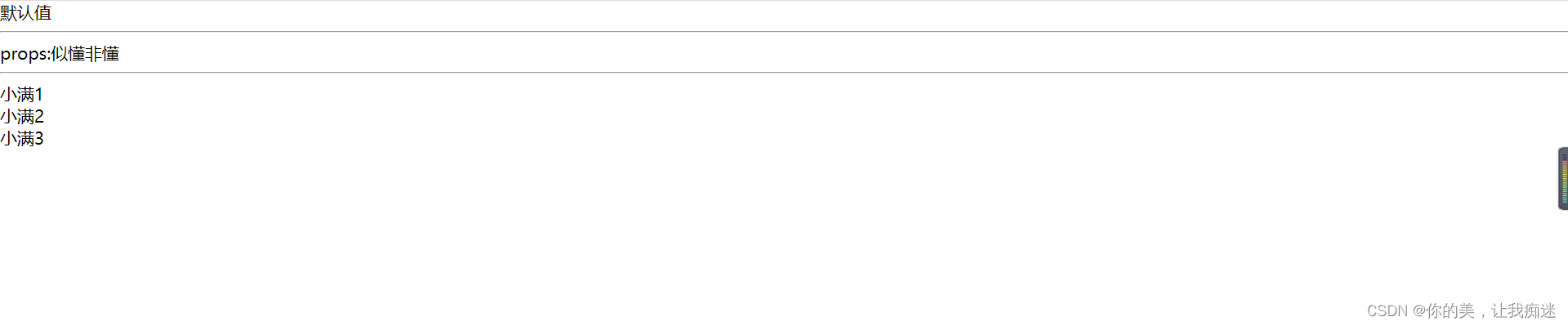
vue3+tsx的使用

<template><div><xiaoman on-click"getItem" name"似懂非懂"></xiaoman></div> </template><script setup langts>import xiaoman from "./App"const getItem(item:any)>{console.log(item,it…...

编程日记 2023/11/28 0:02:28

JMeter 设置请求头信息的详细步骤

在使用 JMeter 的过程中&#xff0c;我们会遇到需要设置请求头信息的场景。比如&#xff1a; POST 传过去的 Body 数据是 json 格式的。需要填添加头信息&#xff1a;Content-Type&#xff1a;application/json。 在 header 中用 token 来传用户的认证信息。 下面&#xff0c;…...

编程日记 2023/11/28 0:01:27

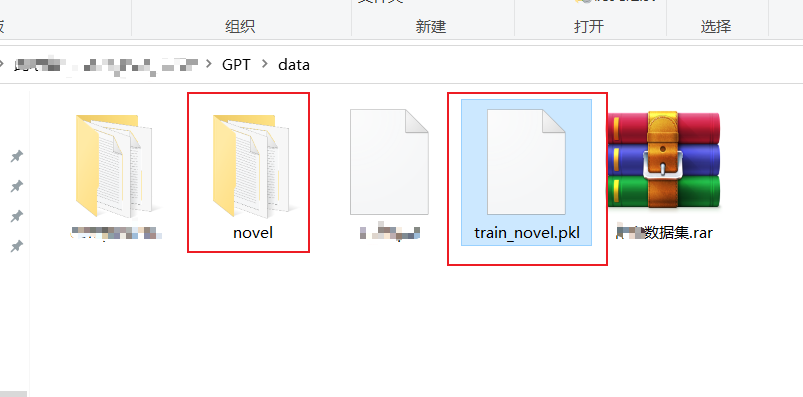
从零构建属于自己的GPT系列1：预处理模块

1 训练数据 在本任务的训练数据中&#xff0c;我选择了金庸的15本小说&#xff0c;全部都是txt文件 数据打开后的样子 2 数据预处理 数据预处理需要做的事情就是使用huggingface的transformers包的tokenizer模块&#xff0c;将文本转化为token 最后生成的文件就是train_n…...

编程日记 2023/11/27 23:59:25

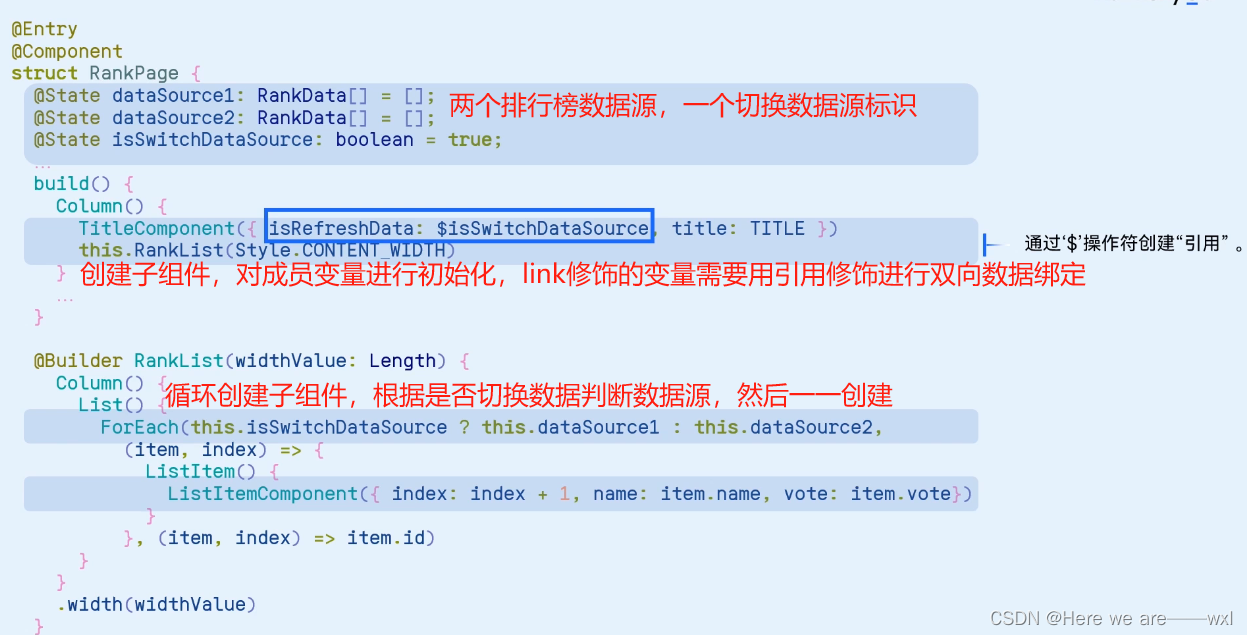
002、ArkTS

之——开发语言 目录 之——开发语言 杂谈 正文 1.TypeScript基础 1.1 基础类型 1.2 条件语句 1.3 函数 1.4 类 1.5 模块 1.6 迭代器 2.ArkTS 2.1 JAVA SCRIPT 2.2 TS 2.3 ArkTS ​编辑 3.示例 3.1 概述性示例 3.2 自定义组件 3.3 渲染控制语法 3.4 状态管…...

编程日记 2023/11/27 23:58:24

如何通过nginx进行服务的负载均衡

简单介绍 随着互联网的发展&#xff0c;业务流量越来越大并且业务逻辑也越来越复杂&#xff0c;单台服务器的性能及单点故障问题就凸显出来了&#xff0c;因此需要多台服务器组成应用集群&#xff0c;进行性能的水平扩展以及避免单点故障的出现。应用集群是将同一应用部署到多台…...

编程日记 2023/11/27 23:57:22

FPGA程序前仿真和后仿真问题处理

参考链接&#xff1a;FPGA程序前仿真和后仿真问题处理 - 知乎...

编程日记 2023/11/27 23:56:22

C语言WFC绘制矩形

代码实现&#xff1a; void CCGDrawingView::Rectangle(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4, COLORREF color,CDC* pDC) {CPen redPen(PS_SOLID, 1, color);CBrush redBursh(color);CPen* pOldPen pDC->SelectObject(&redPen);CBrush* p…...

编程日记 2023/11/27 23:55:20

SpringCloud Alibaba集成 Gateway(自定义负载均衡器)、Nacos(配置中心、注册中心)、loadbalancer

文章目录 POM依赖环境准备配置配置文件配置类 案例展示 POM依赖 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.10</version><relativePath/></p…...

编程日记 2023/11/27 23:54:19

HarmonyOS应用开发者基础认证【题库答案】

HarmonyOS应用开发者高级认证【题库答案】 一、判断 首选项preferences是以Key-Value形式存储数据&#xff0c;其中Key是可以重复。&#xff08;错&#xff09;使用http模块发起网络请求时&#xff0c;必须要使用on(‘headersReceive’&#xff09;订阅请求头&#xff0c;请…...

编程日记 2023/11/27 23:53:18

[pyqt5]pyqt5设置窗口背景图片后上面所有图片都会变成和背景图片一样

pyqt5的控件所有都是集成widget&#xff0c;窗体设置背景图片后控件背景也会跟着改变&#xff0c;此时有2个办法。第一个办法显然我们可以换成其他方式设置窗口背景图片&#xff0c;而不是使用styleSheet样式表&#xff0c;网上有很多其他方法。还有个办法就是仍然用styleSheet…...

编程日记 2023/11/27 23:52:17

【Docker】从零开始：7.Docker命令:容器命令及参数详解

【Docker】从零开始&#xff1a;7.帮助启动类命令 一、帮助启动类命令启动Docker停止Docker重启Docker查看Docker状态开机启动查看docker概要信息查看docker总体帮助文档查看docker命令帮助文档 二、镜像命令列出本地主机上的镜像运行示例返回说明操作参数 搜索仓库里的某个镜像…...

编程日记 2023/11/27 23:50:16

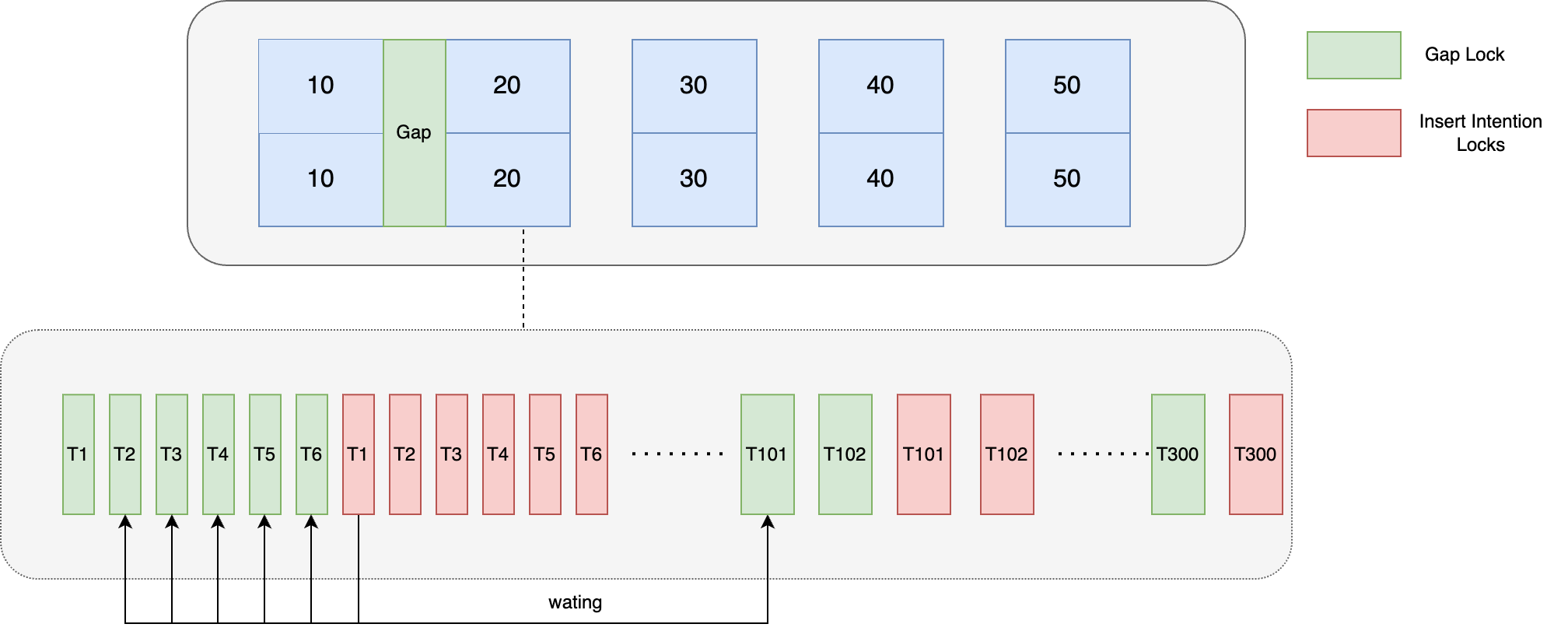
Mysql 锁机制分析

整体业务代码精简逻辑如下&#xff1a; Transaction public void service(Integer id) {delete(id);insert(id); }数据库实例监控&#xff1a; 当时通过分析上游问题流量限流解决后&#xff0c;后续找时间又重新分析了下问题发生的根本原因&#xff0c;现将其总结如下&#xf…...

编程日记 2023/11/27 23:49:15

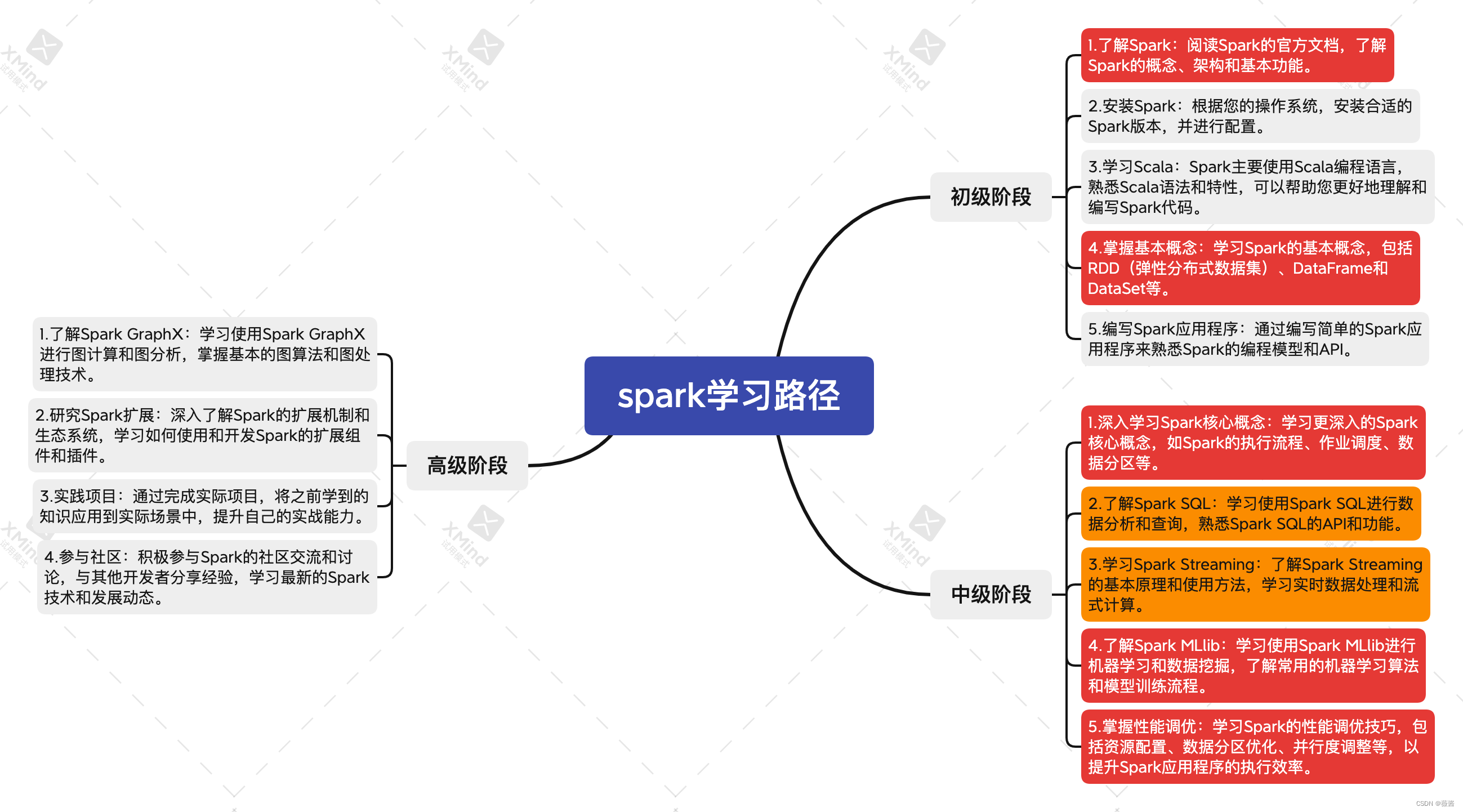
跟着chatgpt学习|1.spark入门

首先先让chatgpt帮我规划学习路径&#xff0c;使用Markdown格式返回&#xff0c;并转成思维导图的形式 目录 目录 1. 了解spark 1.1 Spark的概念 1.2 Spark的架构 1.3 Spark的基本功能 2.spark中的数据抽象和操作方式 2.1.RDD&#xff08;弹性分布式数据集&#xff09; 2…...

编程日记 2023/11/27 23:47:13

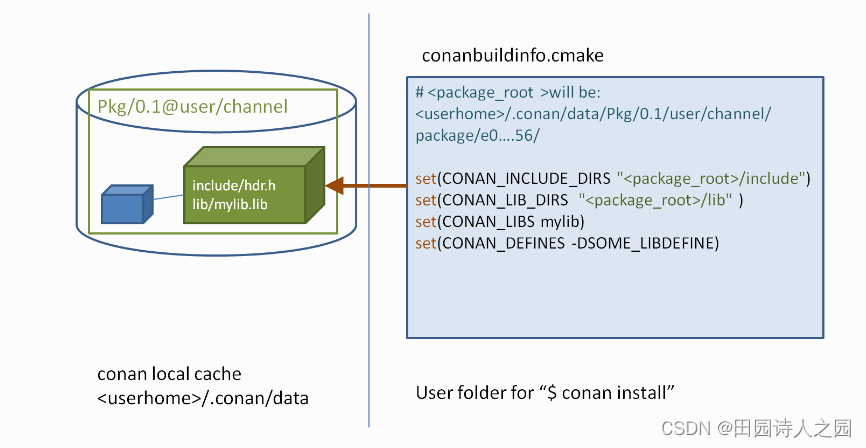
使用conan包 - 安装依赖项

使用conan包 - 安装依赖项 主目录 conan Using packages1 Requires2 Optional user/channel3 Overriding requirements4 Generators5 Options 本文是基于对conan官方文档Installing dependencies的翻译而来&#xff0c; 更详细的信息可以去查阅conan官方文档。 This section s…...

编程日记 2023/11/27 23:46:11

【数据库设计和SQL基础语法】--数据库设计基础--数据规范化和反规范化

一、 数据规范化 1.1 数据规范化的概念 定义 数据规范化是数据库设计中的一种方法&#xff0c;通过组织表结构&#xff0c;减少数据冗余&#xff0c;提高数据一致性和降低更新异常的过程。这一过程确保数据库中的数据结构遵循一定的标准和规范&#xff0c;使得数据存储更加高…...

编程日记 2023/11/27 23:45:10

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题&#xff1a; 下面创建一个简单的Flask RESTful API示例。首先&#xff0c;我们需要创建环境&#xff0c;安装必要的依赖&#xff0c;然后…...

编程新知 2026/2/8 20:42:43

Go 语言接口详解

Go 语言接口详解 核心概念 接口定义 在 Go 语言中&#xff0c;接口是一种抽象类型&#xff0c;它定义了一组方法的集合&#xff1a; // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的&#xff1a; // 矩形结构体…...

编程新知 2026/1/4 5:19:25

蓝桥杯3498 01串的熵

问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798&#xff0c; 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

编程新知 2026/2/6 2:05:50

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

Unity | AmplifyShaderEditor插件基础（第七集：平面波动shader）

目录 一、&#x1f44b;&#x1f3fb;前言 二、&#x1f608;sinx波动的基本原理 三、&#x1f608;波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、&#x1f30a;波动优化…...

编程新知 2026/2/6 22:55:12

力扣-35.搜索插入位置

题目描述 给定一个排序数组和一个目标值&#xff0c;在数组中找到目标值&#xff0c;并返回其索引。如果目标值不存在于数组中&#xff0c;返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

编程新知 2025/12/3 3:22:43

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2026/1/29 14:27:00

springboot整合VUE之在线教育管理系统简介

可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生&#xff0c;小白用户&#xff0c;想学习知识的 有点基础&#xff0c;想要通过项…...

编程新知 2026/1/26 9:30:45

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构&#xff1a;基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中&#xff08;图1&#xff09;&#xff1a; mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59