力扣6:N字形变化

代码:
class Solution {
public:string convert(string s, int numRows){int len=s.size();if(numRows==1){return s;}int d=2*numRows-2;int count=0;string ret;//第一行!for(int i=0;i<len;i+=d){ret+=s[i];}//第k行!for(int i=1;i<numRows-1;i++){for(int j=i,k=d-j;j<len||k<len;j+=d,k+=d){if(j<len){ret+=s[j];}if(k<len){ret+=s[k];}}}//最后一行!for(int i=numRows-1;i<len;i+=d){ret+=s[i];}return ret;}
};算法思路:
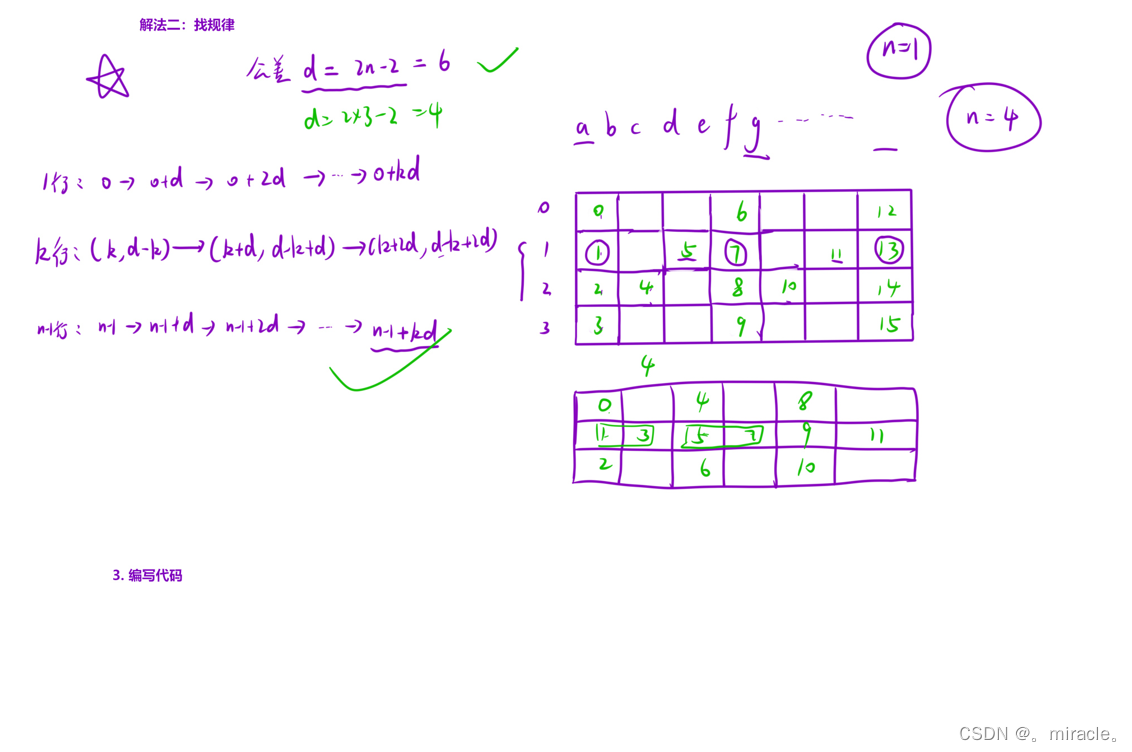
本题可以通过暴力的解法进行求解!即定义一个numsRows行,len列的数组!然后依次根据规律进行将数组元素填置,此时的空间/时间复杂度为O(numsRows*len);
那么是否可以进行优化呢?
答案是肯定的,我们可以通过上图发现一个规律,第i的第一个元素都是i,然后第一行和最后一行有着相同的规律,每隔一个固定的值,会出现一个元素!那么如何求出这个固定的值呢?通过将numsRows我们不难发现!只需要将2*numsRows-2即可求出这个固定的值,我们称之为公差!
为什么是这种求法呢?我们可以将其中间只有一个元素的统一移到第二列,第二列并没有填满,而是只缺少了第一行和最后一行,所以我们不难得到公差d=2*numsRows-2!
所以第一行和最后一行的规律如下:
i---->i+d----->i+2d---.......(直至值大于等于len结束!)
既然第一行和最后一行都发现了规律,那么中间行是否也有规律呢?通过仔细发现,中间行确实也有规律所循!即中间行的第一个元素都和所在行数相同,第二个元素是d-i,这是一组元素!然后每组元素都向后移动的距离仍然还是d! 直接当下标小于原字符串的长度时候结束!
所以第k行的元素有着以下的规律:
(i,d-i)---->(i+d,d-i+d)---->(i+2d,d-1+2d) 直至值大于等于len结束!
还需要注意的边界问题有:当给定的numRows为1!需要直接返回原字符串! 否则就会导致死循环的发生!
相关文章:

力扣6:N字形变化
代码: class Solution { public:string convert(string s, int numRows){int lens.size();if(numRows1){return s;}int d2*numRows-2;int count0;string ret;//第一行!for(int i0;i<len;id){rets[i];}//第k行!for(int i1;i<numRows-1;…...
【上海大学数字逻辑实验报告】一、基本门电路
一、 实验目的 熟悉TTL中、小规模集成电路的外形、管脚和使用方法;了解和掌握基本逻辑门电路的输入与输出之间的逻辑关系及使用规则。 二、 实验原理 实现基本逻辑运算和常用逻辑运算的单元电路称为逻辑门电路。门电路通常用高电平VH表示逻辑值“1”,…...

基于xml配置的AOP
目录 xml方式AOP快速入门 xml方式AOP配置详解 xml方式AOP快速入门 xml方式配置AOP的步骤 导入AOP相关坐标 <dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId><version>1.8.13</version></de…...

java学习part12多态
99-面向对象(进阶)-面向对象的特征三:多态性_哔哩哔哩_bilibili 1.多态(仅限方法) 父类引用指向子类对象。 调用重写的方法,就会执行子类重写的方法。 编译看引用表面类型,执行看实际变量类型。 2.父子同名属性是否…...

前置任务之安装jdk
已经安装过很多次了,但是每次安装都要搜好几次才能找到正确的,离大谱。 1.打开 oracle官网 https://www.oracle.com 然后切换到Java archive 下载192版本的,页面搜索ctrlF,【Java SE Development Kit】或者【jdk-8u192-windows-…...

C++ 常见异常
关于C异常(包括但不限于编译器异常)先开个头,有空都记下来吧: 1:_DllMain12 已经在 MSVCRTD.lib(dllmain.obj) 中定义 有效的解决办法: Debug版本: 项目-属性-链接器-输入:忽略特…...

语音识别学习笔记
目录 开源的语音识别项目 端到端的多说话人语音识别序列化训练方法简介 新一代 Kaldi: Two-pass 实时语音识别 开源的语音识别项目 有哪些语音识别的开源项目? - 知乎 端到端的多说话人语音识别序列化训练方法简介 端到端的多说话人语音识别序列化训练方法简介 …...

深入了解Java8新特性-日期时间API
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概2000多字,预计阅读时间长需要3分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...
【数据结构】二叉树概念 | 满二叉树 | 完全二叉树
二叉树的概念 二叉树在实践中用的很多。 一棵二叉树是结点的一个有限集合,该集合: 或者为空;由一个根结点加上两棵别称为左子树和右子树的二叉树组成。二叉树最多两个孩子。 这里注意:二叉树并不是度为2的树。 二叉树的度最大值是…...

第 373 场 LeetCode 周赛题解
A 循环移位后的矩阵相似检查 模拟 class Solution { public:bool areSimilar(vector<vector<int>> &mat, int k) {int m mat.size(), n mat[0].size();k % n;auto g mat;for (int i 0; i < m; i)if (i & 1)rotate(mat[i].begin(), mat[i].begin() …...

C#,《小白学程序》第二十五课:大数乘法(BigInteger Multiply)的Karatsuba算法及源代码
1 文本格式 /// <summary> /// 《小白学程序》第二十五课:大数(BigInteger)的Karatsuba乘法 /// Multiplies two bit strings X and Y and returns result as long integer /// </summary> /// <param name"a">&…...
Redis的五大数据类型详细用法
我们说 Redis 相对于 Memcache 等其他的缓存产品,有一个比较明显的优势就是 Redis 不仅仅支持简单的key-value类型的数据,同时还提供list,set,zset,hash等数据结构的存储。本篇博客我们就将介绍这些数据类型的详细使用…...
C++类与对象(6)—初始化列表、explicit关键字、static成员
目录 一、初始化列表 1、定义 2、注意事项 3、尽量使用初始化列表初始化 4、初始化顺序 二、 explicit关键字 1、定义 2、特点 三、static成员 1、定义 2、特性 3、例题 一、初始化列表 下面这段代码可以正常编译: class A { private:int _a1;//成员…...
vue3+tsx的使用
<template><div><xiaoman on-click"getItem" name"似懂非懂"></xiaoman></div> </template><script setup langts>import xiaoman from "./App"const getItem(item:any)>{console.log(item,it…...

JMeter 设置请求头信息的详细步骤
在使用 JMeter 的过程中,我们会遇到需要设置请求头信息的场景。比如: POST 传过去的 Body 数据是 json 格式的。需要填添加头信息:Content-Type:application/json。 在 header 中用 token 来传用户的认证信息。 下面,…...
从零构建属于自己的GPT系列1:预处理模块
1 训练数据 在本任务的训练数据中,我选择了金庸的15本小说,全部都是txt文件 数据打开后的样子 2 数据预处理 数据预处理需要做的事情就是使用huggingface的transformers包的tokenizer模块,将文本转化为token 最后生成的文件就是train_n…...
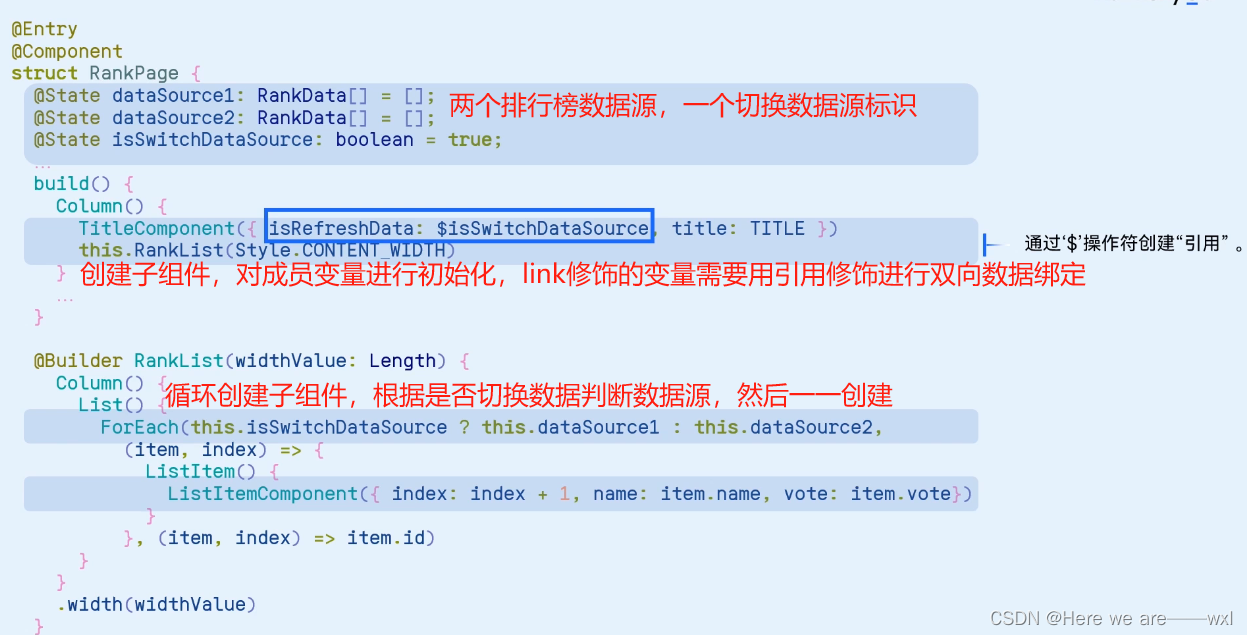
002、ArkTS
之——开发语言 目录 之——开发语言 杂谈 正文 1.TypeScript基础 1.1 基础类型 1.2 条件语句 1.3 函数 1.4 类 1.5 模块 1.6 迭代器 2.ArkTS 2.1 JAVA SCRIPT 2.2 TS 2.3 ArkTS 编辑 3.示例 3.1 概述性示例 3.2 自定义组件 3.3 渲染控制语法 3.4 状态管…...

如何通过nginx进行服务的负载均衡
简单介绍 随着互联网的发展,业务流量越来越大并且业务逻辑也越来越复杂,单台服务器的性能及单点故障问题就凸显出来了,因此需要多台服务器组成应用集群,进行性能的水平扩展以及避免单点故障的出现。应用集群是将同一应用部署到多台…...

FPGA程序前仿真和后仿真问题处理
参考链接:FPGA程序前仿真和后仿真问题处理 - 知乎...
C语言WFC绘制矩形
代码实现: void CCGDrawingView::Rectangle(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4, COLORREF color,CDC* pDC) {CPen redPen(PS_SOLID, 1, color);CBrush redBursh(color);CPen* pOldPen pDC->SelectObject(&redPen);CBrush* p…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
