Jacobi迭代与SOR迭代求解希尔伯特矩阵
给出线性方程组 Hn*x = b,其中系数矩阵Hn为希尔伯特矩阵:
假设 x ∗ =(1, 1, . . . , 1)T,b = Hnx ∗。若取 n = 6,8, 10,分别用 Jacobi
迭代法及 SOR迭代(ω = 1, 1:25,1:5)求解,比较计算结果。
MATLAB源码如下,运行Demo_Jacobi_SOR.m文件,附件包含另外两个函数文件,分别为:Jacobi.m与SOR.m。
Demo_Jacobi_SOR.m
clear all
clc
n=[6 8 10];
for i=1:length(n)
H{i}=hilb(n(i));
size_H{i}=size(H{i},1);
x_true{i}=ones(1,size_H{i});
b{i}=x_true{i}*H{i};
x_ini{i}=zeros(1,size_H{i});
%accuracy=5*(10^-6);
accuracy=0.01;
end
%Jacobi
disp('Jacobi');
for i=1:length(n)
fprintf('The dimension is %d\n',n(i))
[x{i},k{i}]=Jacobi(H{i},b{i},x_ini{i},accuracy,x_true{i});
end
%SOR
disp('SOR');
w=1;
disp('SOR w=1');
for i=1:length(n)
fprintf('The dimension is %d\n',n(i))
[q{i},e{i}]=SOR(H{i},b{i},x_ini{i},accuracy,x_true{i},w);
end
w=1.25;
disp('SOR w=1.25');
for i=1:length(n)
fprintf('The dimension is %d\n',n(i))
[z{i},x{i}]=SOR(H{i},b{i},x_ini{i},accuracy,x_true{i},w);
end
w=1.5;
disp('SOR w=1.5');
for i=1:length(n)
fprintf('The dimension is %d\n',n(i))
[v{i},b{i}]=SOR(H{i},b{i},x_ini{i},accuracy,x_true{i},w);
end
%[x,k]=Jacobi(A,b,x_ini,accuracy,x_true);
Jacobi.m
function [x,k]=Jacobi(A,b,x_ini,accuracy,x_true)
% input: A—Left Matrix
% b—Right Matrix
% x_ini—initial value
% accuracy—calculation precision between solution and true value
% x_true—true valuer
% output: x—solution
% k—iteration-1
n=size(A,1);
uint16 k;
k=1;
x{1}=x_ini;
while(norm(x_true-x{k},Inf)>=accuracy)
k=k+1;
%disp(k-1);
for i=1:1:n
temp1=0;
for j=1:1:i-1
temp1=temp1+A(i,j)*x{k-1}(j);
end
temp2=0;
for j=i+1:1:n
temp2=temp2+A(i,j)*x{k-1}(j);
end
x{k}(i)=(b(i)-temp1-temp2)/A(i,i);
end
if (k==200000)
break;
end
end
fprintf('The iteration k=%d\n',k-1);
disp('The solution is');
disp(x{k});
end
SOR.m
function [x,k]=SOR(A,b,x_ini,accuracy,x_true,w)
% input: A—Left Matrix
% b—Right Matrix
% x_ini—initial value
% accuracy—calculation precision between solution and true value
% x_true—true value
% w—relaxation factor
% output: x—solution
% k—iteration-1
n=size(A,1);
uint16 k;
k=1;
x{1}=x_ini;
while(norm(x_true-x{k},Inf)>accuracy)
k=k+1;
%disp(k-1);
for i=1:1:n
temp1=0;
if(i>1)
for j=1:1:i-1
temp1=temp1+A(i,j)*x{k}(j);
end
end
temp2=0;
for j=i:1:n
temp2=temp2+A(i,j)*x{k-1}(j);
end
x{k}(i)=x{k-1}(i)+w*(b(i)-temp1-temp2)/A(i,i);
end
if (k==200000)
break;
end
end
fprintf('The iteration k=%d\n',k-1);
disp('The solution is');
disp(x{k});
end
MATLAB运行结果为:
Jacobi
The dimension is 6
The iteration k=199999
The solution is
Inf Inf Inf Inf Inf Inf
The dimension is 8
The iteration k=199999
The solution is
Inf Inf Inf Inf Inf Inf Inf Inf
The dimension is 10
The iteration k=199999
The solution is
Inf Inf Inf Inf Inf Inf Inf Inf Inf Inf
SOR
SOR w=1
The dimension is 6
The iteration k=14508
The solution is
0.9999 1.0016 0.9957 0.9994 1.0100 0.9933
The dimension is 8
The iteration k=42694
The solution is
1.0001 0.9984 1.0076 0.9900 0.9971 1.0073 1.0068 0.9926
The dimension is 10
The iteration k=25508
The solution is
1.0001 0.9980 1.0065 0.9985 0.9912 0.9970 1.0057 1.0091 1.0039 0.9900
SOR w=1.25
The dimension is 6
The iteration k=82840
The solution is
1.0000 0.9995 1.0036 0.9908 1.0100 0.9961
The dimension is 8
The iteration k=50752
The solution is
1.0001 0.9984 1.0073 0.9900 0.9983 1.0064 1.0060 0.9934
The dimension is 10
The iteration k=26267
The solution is
1.0001 0.9983 1.0048 1.0012 0.9900 0.9971 1.0053 1.0087 1.0038 0.9906
SOR w=1.5
The dimension is 6
The iteration k=174587
The solution is
1.0000 0.9994 1.0036 0.9908 1.0100 0.9961
The dimension is 8
The iteration k=52211
The solution is
1.0001 0.9985 1.0071 0.9900 0.9996 1.0049 1.0059 0.9939
The dimension is 10
The iteration k=199999
The solution is
1.0000 1.0007 0.9954 1.0113 0.9909 0.9986 0.9993 1.0049 1.0026 0.9962
运行结果分析:
用雅克比迭代法进行线性方程系数矩阵为希尔伯特矩阵的求解,解是发散的,最终趋于无穷大。
用SOR迭代法进行线性方程系数矩阵为希尔伯特矩阵的求解,解是收敛的,且收敛速度与矩阵的大小有关,但不是单调性的正相关或者负相关关系。
相关文章:

Jacobi迭代与SOR迭代求解希尔伯特矩阵
给出线性方程组 Hn*x b,其中系数矩阵Hn为希尔伯特矩阵: 假设 x ∗ (1, 1, . . . , 1)T,b Hnx ∗。若取 n 6,8, 10,分别用 Jacobi 迭代法及 SOR迭代(ω 1, 1:25,1:5)求解,比较计算结果。…...

【云备份】配置加载文件模块
文章目录 配置信息设计配置文件加载cloud.conf配置文件单例模式的使用ReadConfigFile —— 读取配置文件GetInstance —— 创建对象其他函数的实现 具体实现cloud.confconfig.hpp 配置信息设计 使用文件配置加载一些程序运行的关键信息 可以让程序的运行更加灵活 配置信息&am…...

sqlserver写入中文乱码问题
sqlserver写入中文乱码问题解决方案 首先查看sqlserver数据库编码 首先查看sqlserver数据库编码 查询语句:SELECT COLLATIONPROPERTY(Chinese_PRC_Stroke_CI_AI_KS_WS, CodePage); 对应的编码: 936 简体中文GBK 950 繁体中文BIG5 437 美国/加…...

【亚马逊云】基于EC2以 All-in-One 模式快速部署 KubeSphere 和 Kubernetes
文章目录 1. 云实例配置说明2. SSH连接云实例3. 查看系统版本4. 修改主机名5. 安装依赖项6. 安全组和DNS修改7. 下载KubeKey8. 同时安装Kubesphere和Kubernetes[可选]单独安装Kubernetes[可选]单独安装KubeSphere9. 验证KubeSphere安装结果10. 登录KubeSphere控制台[可选]安装K…...

使用 ChatGPT 创建 Makefile 构建系统:从 Docker 开始
使用 Docker 搭配 ChatGPT 创建 Makefile 构建系统 Makefile 构建系统是嵌入式软件团队实现其开发流程现代化的基础。构建系统不仅允许开发人员选择各种构建目标,还可以将这些构建集成到持续集成/持续部署 (CI/CD) 流程中。使用诸如 ChatGPT 这样的人工智能 (AI) 工…...

嵌入式设备摄像头基础知识
工作原理 摄像头的工作原理是,当光线通过镜头聚焦到图像传感器上时,传感器会将光信号转换为电信号,并将其传输给处理器进行处理。处理器通过算法对图像信号进行增强、去噪、压缩等操作,并将其转换为数字信号输出给计算机或其他设…...

使用Pytorch从零开始构建Normalizing Flow
归一化流 (Normalizing Flow) (Rezende & Mohamed,2015)学习可逆映射 f : X → Z f: X \rightarrow Z f:X→Z, 在这里X是我们的数据分布,Z是选定的潜在分布。 归一化流是生成模型家族的一部分,其中包括变分自动编…...

一个tomcat中部署的多个war,相当于几个jvm
请直接去看原文 原文链接:一个tomcat有几个jvm-CSDN博客 --------------------------------------------------------------------------------------------------------------------------------- 前几天向unmi提问,今天他答复了。我觉得答复很清楚,…...
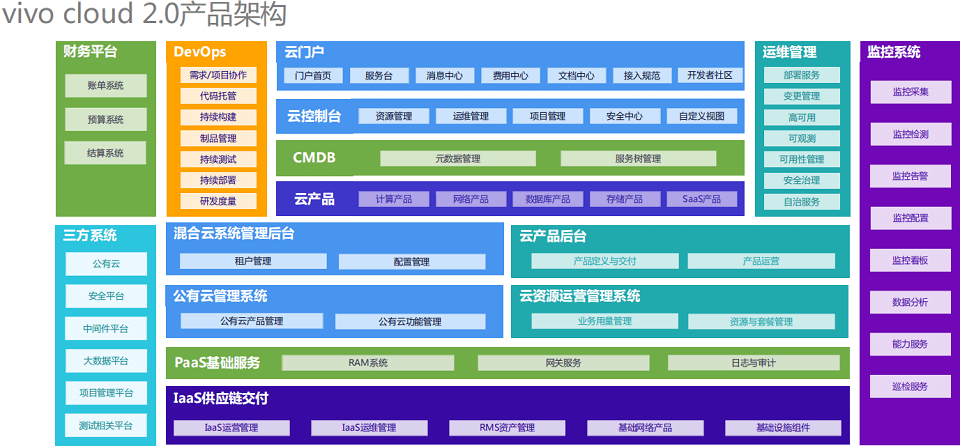
2023年第十六届中国系统架构师大会(SACC2023)-核心PPT资料下载
一、峰会简介 本届大会以“数字转型 架构演进”为主题, 涵盖多个热门领域,如多云多活、海量分布式存储、容器、云成本、AIGC大数据等,同时还关注系统架构在各个行业中的应用,如金融、制造业、互联网、教育等。 与往届相比&#…...
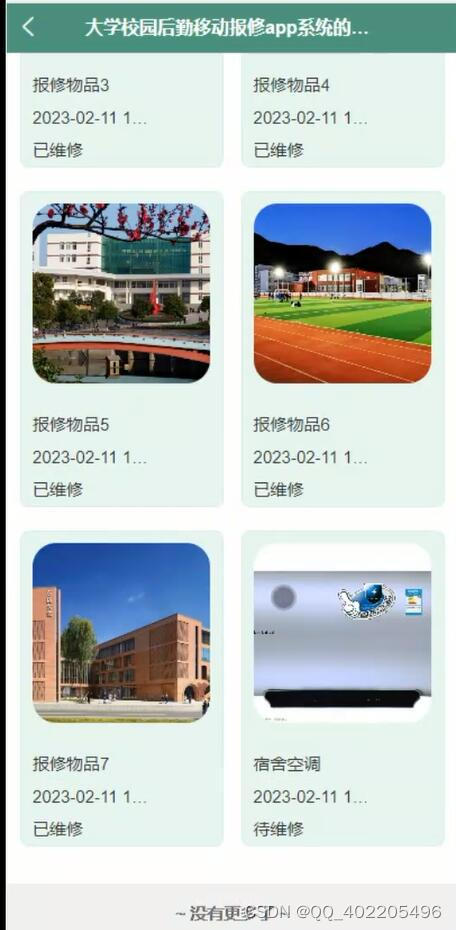
高校大学校园后勤移动报修系统 微信小程序uniapp+vue
本文主要是针对线下校园后勤移动报修传统管理方式中管理不便与效率低的缺点,将电子商务和计算机技术结合起来,开发出管理便捷,效率高的基于app的大学校园后勤移动报修app。该系统、操作简单、界面友好、易于管理和维护;而且对后勤…...

docker常见问题汇总
docker常见问题 ❓问题1:启动docker容器时,报错Unknown runtime specified nvidia. 当我启动一个容器时,运行以下命令: docker run --runtimenvidia 。。。。 后面一部分命令没写出来,此时报错的信息如下:…...

JMeter 测试脚本编写技巧
JMeter 是一款开源软件,用于进行负载测试、性能测试及功能测试。测试人员可以使用 JMeter 编写测试脚本,模拟多种不同的负载情况,从而评估系统的性能和稳定性。以下是编写 JMeter 测试脚本的步骤。 第 1 步:创建测试计划 在JMet…...
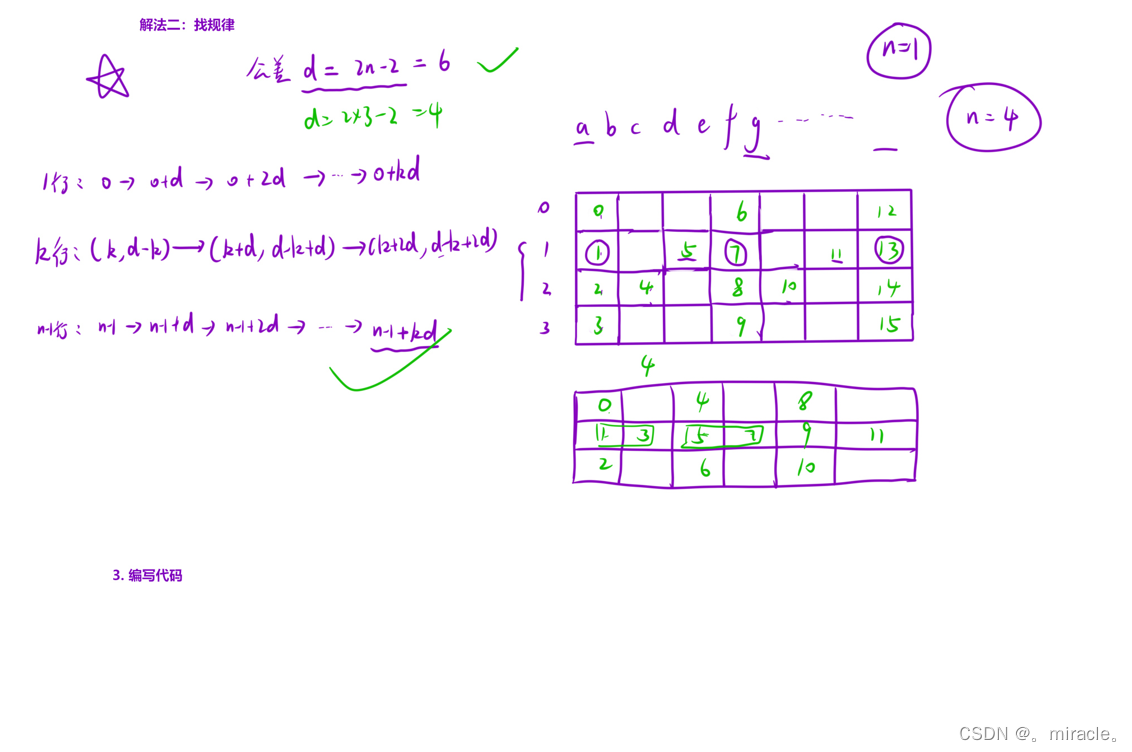
力扣6:N字形变化
代码: class Solution { public:string convert(string s, int numRows){int lens.size();if(numRows1){return s;}int d2*numRows-2;int count0;string ret;//第一行!for(int i0;i<len;id){rets[i];}//第k行!for(int i1;i<numRows-1;…...
【上海大学数字逻辑实验报告】一、基本门电路
一、 实验目的 熟悉TTL中、小规模集成电路的外形、管脚和使用方法;了解和掌握基本逻辑门电路的输入与输出之间的逻辑关系及使用规则。 二、 实验原理 实现基本逻辑运算和常用逻辑运算的单元电路称为逻辑门电路。门电路通常用高电平VH表示逻辑值“1”,…...

基于xml配置的AOP
目录 xml方式AOP快速入门 xml方式AOP配置详解 xml方式AOP快速入门 xml方式配置AOP的步骤 导入AOP相关坐标 <dependency><groupId>org.aspectj</groupId><artifactId>aspectjweaver</artifactId><version>1.8.13</version></de…...

java学习part12多态
99-面向对象(进阶)-面向对象的特征三:多态性_哔哩哔哩_bilibili 1.多态(仅限方法) 父类引用指向子类对象。 调用重写的方法,就会执行子类重写的方法。 编译看引用表面类型,执行看实际变量类型。 2.父子同名属性是否…...

前置任务之安装jdk
已经安装过很多次了,但是每次安装都要搜好几次才能找到正确的,离大谱。 1.打开 oracle官网 https://www.oracle.com 然后切换到Java archive 下载192版本的,页面搜索ctrlF,【Java SE Development Kit】或者【jdk-8u192-windows-…...

C++ 常见异常
关于C异常(包括但不限于编译器异常)先开个头,有空都记下来吧: 1:_DllMain12 已经在 MSVCRTD.lib(dllmain.obj) 中定义 有效的解决办法: Debug版本: 项目-属性-链接器-输入:忽略特…...

语音识别学习笔记
目录 开源的语音识别项目 端到端的多说话人语音识别序列化训练方法简介 新一代 Kaldi: Two-pass 实时语音识别 开源的语音识别项目 有哪些语音识别的开源项目? - 知乎 端到端的多说话人语音识别序列化训练方法简介 端到端的多说话人语音识别序列化训练方法简介 …...

深入了解Java8新特性-日期时间API
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概2000多字,预计阅读时间长需要3分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
