当前位置：首页 > news >正文

诺威信，浪潮云，微众区块链

news 2026/2/10 8:50:39

诺威信B隐私计算平台

浪潮云=星火连-澳优码

HyperChain

产品介绍

CA认证即电子认证服务

诺威信，浪潮云，微众区块链

目录诺威信B隐私计算平台浪潮云=星火连-澳优码 HyperChain 产品介绍 CA认证即电子认证服务...

编程日记 2023/11/28 2:18:18

Redux在React中的使用

Redux在React中的使用 1.构建方式采用reduxjs/toolkitreact-redux的方式安装方式 npm install reduxjs/toolkit react-redux2.使用 ①创建目录创建store文件夹，然后创建index和对应的模块，如上图所示 ②编写counterStore.js 文章以counterStore…...

编程日记 2023/11/28 2:17:15

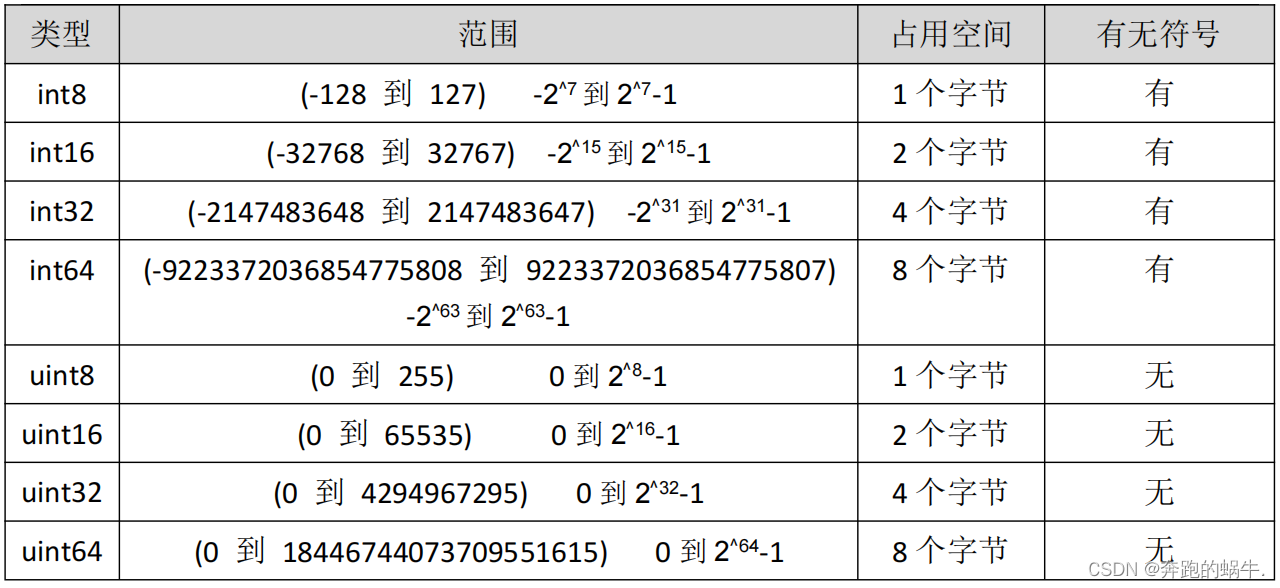
Go 数字类型

一、数字类型 1、Golang 数据类型介绍 Go 语言中数据类型分为：基本数据类型和复合数据类型基本数据类型有： 整型、浮点型、布尔型、字符串复合数据类型有： 数组、切片、结构体、函数、map、通道（channel）、接口 2、…...

编程日记 2023/11/28 2:15:11

时间序列预测 — Informer实现多变量负荷预测(PyTorch)

目录 1 实验数据集 2 如何运行自己的数据集 3 报错分析 1 实验数据集实验数据集采用数据集4：2016年电工数学建模竞赛负荷预测数据集（下载链接），数据集包含日期、最高温度℃ 、最低温度℃、平均温度℃ 、相对湿度(平均) 、降雨…...

编程日记 2023/11/28 2:14:09

2023年金融信创行业研究报告

第一章行业概况 1.1 定义金融信创是指在金融行业中应用的信息技术，特别是那些涉及到金融IT基础设施、基础软件、应用软件和信息安全等方面的技术和产品。这一概念源于更广泛的“信创 (信息技术应用创新)”，即通过中国国产信息技术替换海外信息技术&a…...

编程日记 2023/11/28 2:12:08

51单片机按键控制LED灯亮灭的N个玩法

51单片机按键控制LED灯亮灭的N个玩法 1.概述这篇文章介绍按键的使用，以及通过控制LED灯的小实验，发现按键中存在的问题，然后思考并解决这些问题。达到熟练使用按键控制元器件。 2.搭建硬件环境 1.硬件准备名称型号数量单片机STC12C205…...

编程日记 2023/11/28 2:10:06

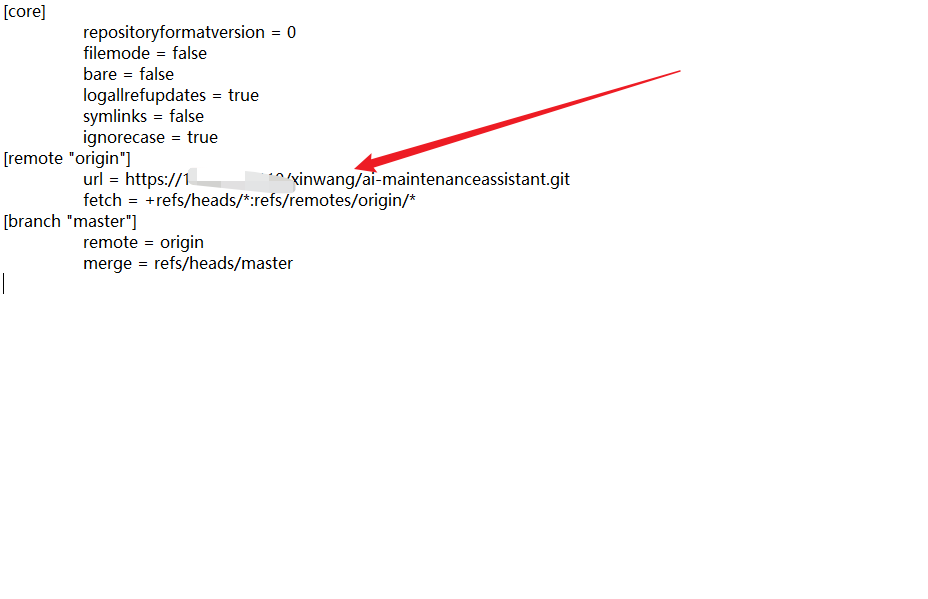
【Git】git 更换远程仓库地址三种方法总结分享

因为公司更改了 gitlab 的网段地址，发现全部项目都需要重新更改远程仓库的地址了，所以做了个记录，说不定以后还会用到呢。一、不删除远程仓库修改（最方便） # 查看远端地址 git remote -v # 查看远端仓库名 git rem…...

编程日记 2023/11/28 2:08:03

springboot 返回problem+json

spring所有配置都在WebMvcAutoConfiguration中其中有 ProblemDetailsExceptionHandler 容器中的一个组件 -ControllerAdvice用来集中处理异常的 -点进ResponseEntityExceptionHandler 包含这些异常，如果出现以下异常，会被springboot支持以RFC 7807规…...

编程日记 2023/11/28 2:07:02

1.brew -v 2.安装爬虫项目包所必需的python和git等系列系统支持部件 brew install cmake protobuf rust python@3.10 git wget pod --version brew link --overwrite cocoapods 3.从github网站克隆stable-diffusion-webui爬虫项目包至本地 ssh-add /Users/haijunyan/.ssh/id_r…...

编程日记 2023/11/28 2:05:59

【开源】基于Vue和SpringBoot的木马文件检测系统

项目编号： S 041 ，文末获取源码。 \color{red}{项目编号：S041，文末获取源码。} 项目编号：S041，文末获取源码。目录一、摘要1.1 项目介绍1.2 项目录屏二、功能模块2.1 数据中心模块2.2 木马分类模块2.3 木…...

编程日记 2023/11/28 2:04:57

5 动态规划解分割等和子串

来源：LeetCode第416题难度：中等描述：给你一个只包含正整数的非空数组nums,请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等分析：相当于从nums数组中选取一些元素，使得他们的和为…...

编程日记 2023/11/28 2:03:56

file_get_contents() 函数详解与使用

概述在PHP中，file_get_contents() 函数是一个强大的工具，它既可以用于读取本地文件的内容，也可以用于发起 HTTP 请求获取远程资源。本文将详细介绍 file_get_contents() 函数的两种主要用途，并探讨如何充分利用这个函数。 1. 文…...

编程日记 2023/11/28 2:02:55

某医生用 ChatGPT 在 4 个月内狂写 16 篇论文，其中 5 篇已发表，揭密ChatGPT进行论文润色与改写的秘籍

如果写过学术论文，想必会有这样的感受： 绞尽脑汁、茶饭不思、夜不能寐、废寝忘食、夜以继日，赶出一篇论文，然后还被导师点评，“写得就是一坨！” 可是，却有人4个月产出了16篇论文，成功…...

编程日记 2023/11/28 2:01:54

进程等待讲解

今日为大家分享有关进程等待的知识！希望读完本文，大家能有一定的收获！ 正文开始！ 进程等待的引进既然我们今天要讲进程等待这个概念！那么只有我们把下面这三个方面搞明白，才能真正的了解进程等待&#x…...

编程日记 2023/11/28 2:00:53

MySQL Binlog深度解析：进阶应用与实战技巧【进阶应用】

🎏：你只管努力，剩下的交给时间 🏠 ：小破站 MySQL Binlog深度解析：进阶应用与实战技巧前言第一：Binlog事件详解第二：关于GTIDGTID的结构：GTID的作用：GTID的事…...

编程日记 2023/11/28 1:58:49

openpnp - 给底部相机加防尘罩

文章目录 openpnp - 给底部相机加防尘罩概述笔记END openpnp - 给底部相机加防尘罩概述设备标定完, 看着底部相机, 有点担心掉进去东西, 万一从吸嘴掉下去的料(或者清理设备台面时, 不小心掉进去东西)将顶部相机搞短路怎么办. 就想加个防尘罩, 如果有东西掉进去, 可以掉到机…...

编程日记 2023/11/28 1:57:48

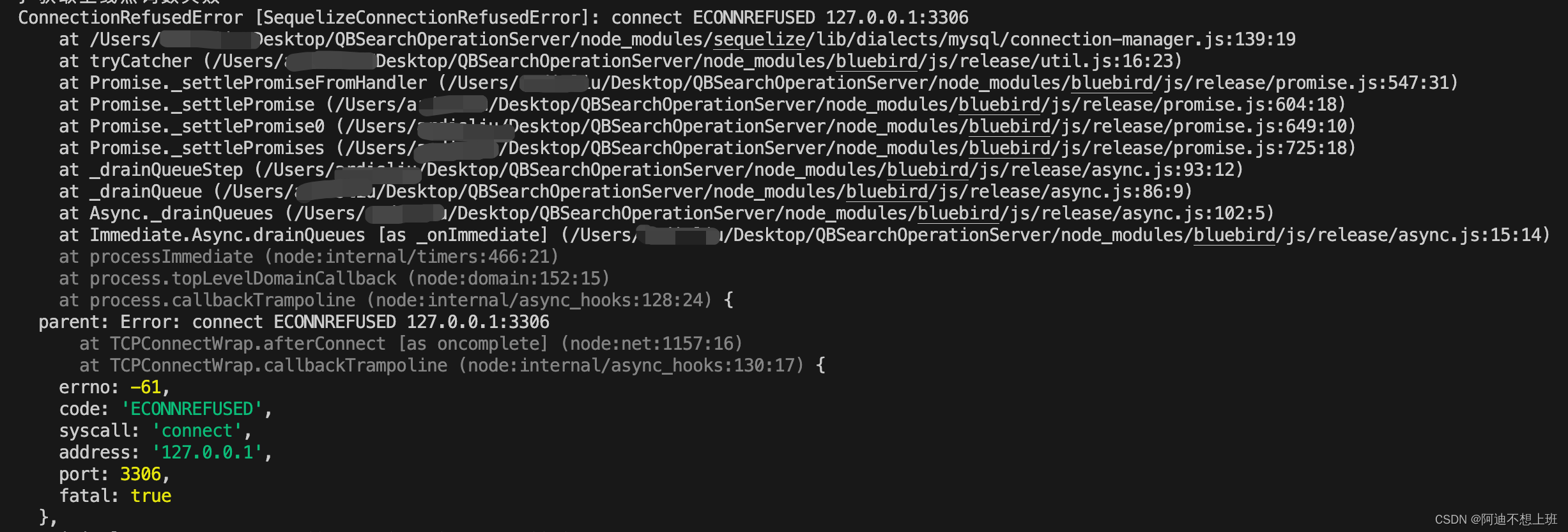
mac mysql连接中断重新启动办法

遇到如图所示问题，可以用下面的命令重启mysql服务 sudo /usr/local/mysql/support-files/mysql.server start...

编程日记 2023/11/28 1:55:44

【Vue3】解决Vue打包后上传服务器资源路径加载错误

问题： 我这里在打包Vue之后将打包后的dist 上传至服务器站点根目录内子目录名为 "adminstore" , 但是当我通过域名打开站点后发现资源加载路径内并没有携带子目录 "adminstore" 文件名称错误：http://your website domain/js/app…...

编程日记 2023/11/28 1:54:43

u-popup组件在UniApp中的讲解

u-popup 组件是 UniApp 中一个多功能且强大的组件，UniApp 是一个使用 Vue.js 开发跨平台应用程序的框架。u-popup 组件提供了一种在应用程序的其他内容上方显示临时或浮动内容的方式。使用方法： 要在 UniApp 项目中使用 u-popup 组件，你需要…...

编程日记 2023/11/28 1:53:42

Python｜GIF 解析与构建（5）：手搓截屏和帧率控制

目录 Python｜GIF 解析与构建（5）：手搓截屏和帧率控制一、引言二、技术实现：手搓截屏模块 2.1 核心原理 2.2 代码解析：ScreenshotData类 2.2.1 截图函数：capture_screen 三、技术实现&…...

编程新知 2025/11/14 3:06:30

中南大学无人机智能体的全面评估！BEDI：用于评估无人机上具身智能体的综合性基准测试

作者：Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位：中南大学地球科学与信息物理学院论文标题：BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接：https://arxiv.…...

编程新知 2026/1/22 15:36:10

智能在线客服平台：数字化时代企业连接用户的 AI 中枢

随着互联网技术的飞速发展，消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁，不仅优化了客户体验，还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用，并…...

编程新知 2026/2/4 17:51:19

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化之前初步学习prophet的时候，写过一篇简单实现，后期随着对该模型的深入研究，本次记录涉及到prophet 的公式以及参数调优，从公式可以更直观…...

编程新知 2026/1/27 5:01:54

P3 QT项目----记事本（3.8）

3.8 记事本项目总结项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36