【数据结构】图<简单认识图>
对于下面的内容,大家着重观察和理解图即可,可以直接绕过一些文字性的概念,对图有一个大概的认识。
图
- 简单认识图
- 图的定义
- 有向图和无向图
- 完全图
- 无向完全图
- 有向完全图
- 图的基本存储结构
- 邻接矩阵存储
- 邻接矩阵的优点
- 网络的邻接矩阵
- 邻接表
- 无向图的邻接表
- 有向图的邻接表
- 关于顶点的度、出度与入度
简单认识图
图,是一种比树更为复杂的数据结构。树的节点之间是一对多的关系,并且存在父与子的层级划分;而图的顶点(注意,这里不叫节点)之间是多对多的关系,并且所有顶点都是平等的,无所谓谁是父谁是子。
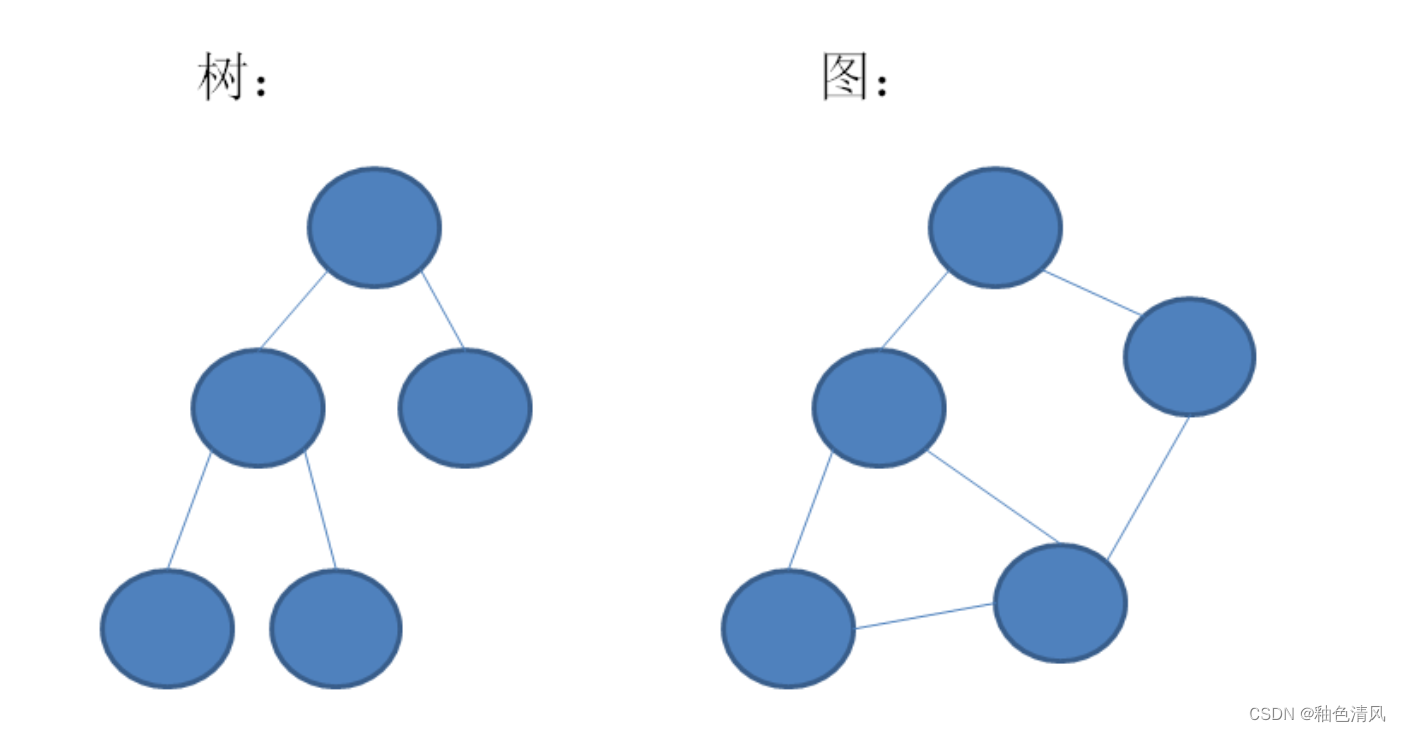
图的定义
图 是由一个非空的顶点集合和一个描述顶点之间多对多关系的边(或弧)集合组成的一种数据结构,它可以形式化地表示为: 图=(V,E
其中V={x|x∈某个数据对象集},它是顶点的有穷非空集合;E={(x,y)|x,y∈V}或E={<x,y>|x,y∈V且P(x,y)},它是顶点之间关系的有穷集合,也叫做边集合,P(x,y)表示从x到y的一条单向通路。
有向图和无向图
若图G中的每条边都是有方向的,则称G为有向图。在有向图中,一条有向边是由两个顶点组成的有序对,有序对通常用尖括号表示。例如,有序对<vi,vj>表示一条由vi到vj的有向边。有向边又称为弧,弧的始点称为弧尾,弧的终点称为弧头。若图G中的每条边都是没有方向的,则称G为无向图。无向图中的边均是顶点的无序对,无序对通常用圆括号表示。
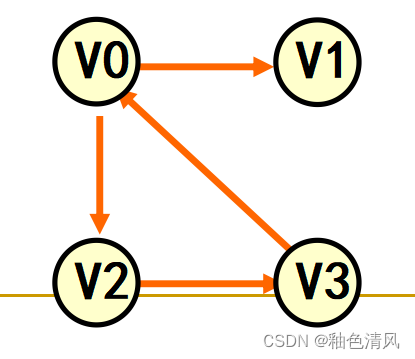
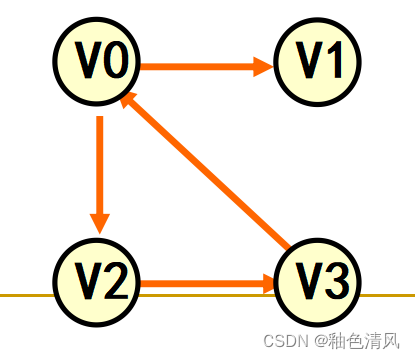
下面我们举例说明:
①如下图所示,顶点集合V(G1)={ V 0 , V 1 , V 2 , V 3 , V 4 V_0,V_1,V_2,V_3,V_4 V0,V1,V2,V3,V4}
边集合为E(G1)={ ( V 0 , V 1 ) , ( V 0 , V 3 ) , ( V 1 , V 2 ) , ( V 1 , V 4 ) , ( V 2 , V 3 ) , ( V 2 , V 4 ) (V_0,V_1),(V_0,V_3),(V_1,V_2),(V_1,V_4),(V_2,V_3),(V_2,V_4) (V0,V1),(V0,V3),(V1,V2),(V1,V4),(V2,V3),(V2,V4)} 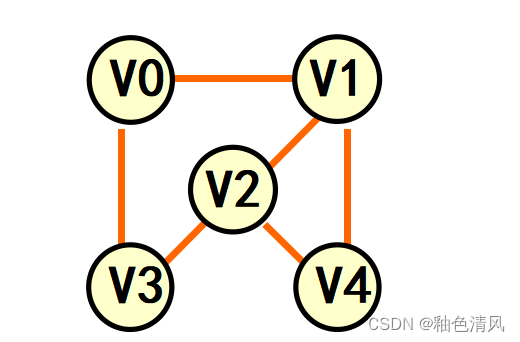
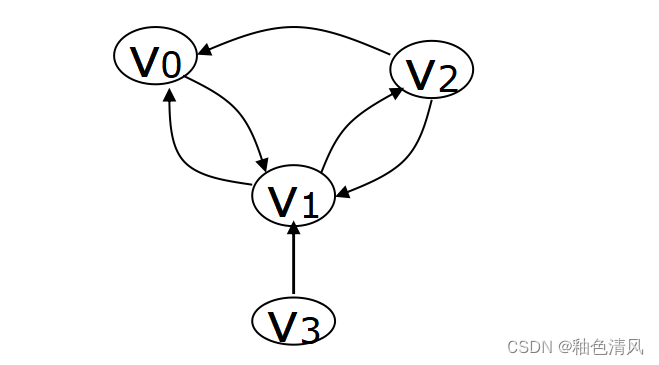
②如下图所示,顶点集合V(G2)={ V 0 , V 1 , V 2 , V 3 V_0,V_1,V_2,V_3 V0,V1,V2,V3}
边集合为E(G2)={ < V 0 , V 1 > , < V 0 , V 2 > , < V 2 , V 3 > , < V 3 , V 0 > <V_0,V_1>,<V_0,V_2>,<V_2,V_3>,<V_3,V_0> <V0,V1>,<V0,V2>,<V2,V3>,<V3,V0>}

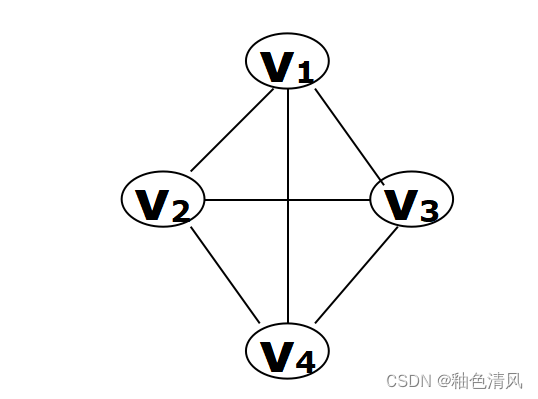
完全图
简单来说,完全图具有最多的边数,任意一对顶点间均有边相连。
无向完全图
对于具有n个顶点的完全图,如果每两个顶点之间都有相连,也就是边数为
e= ( n − 1 ) + ( n − 2 ) + . . . + 1 (n-1)+(n-2)+...+1 (n−1)+(n−2)+...+1= n ( n − 1 ) 2 \frac{n(n-1)}{2} 2n(n−1),就是完全图,否则,就是不完全图。
如下图所示,即为无向完全图。
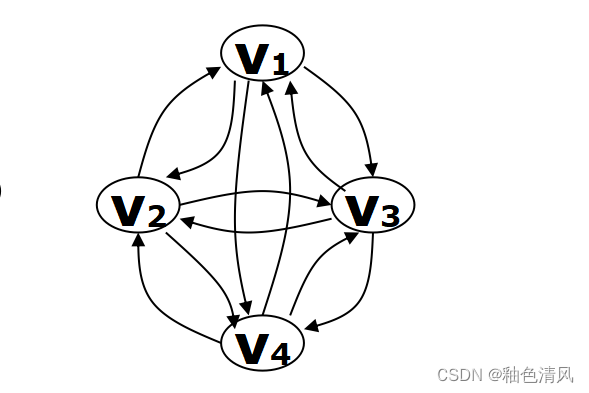
有向完全图
对于具有n个顶点的完全图,如果每两个顶点之间都有相连,也就是边数为n(n-1),那么即为有向完全图。
如下图所示,即为有向完全图。
图的基本存储结构
图的存储结构至少要保存两类信息:
1)顶点的数据
2)顶点间的关系
邻接矩阵存储
给定图G=(V,E),其中V(G)={v0,…,vi,…,vn-1},G的邻接矩阵(Adacency Matrix)是具有如下性质的n阶方阵:

下面,我们举例说明:
写出如下两个图的邻接矩阵。
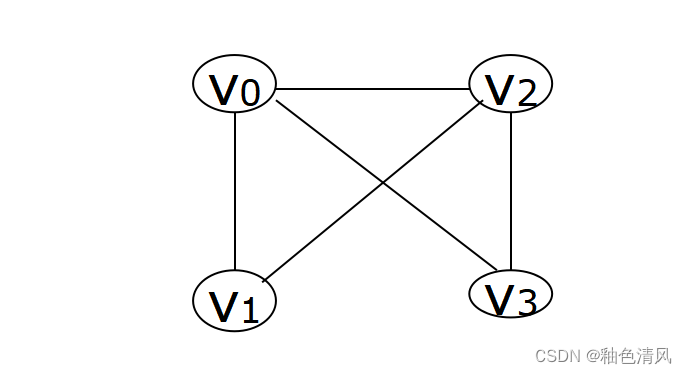
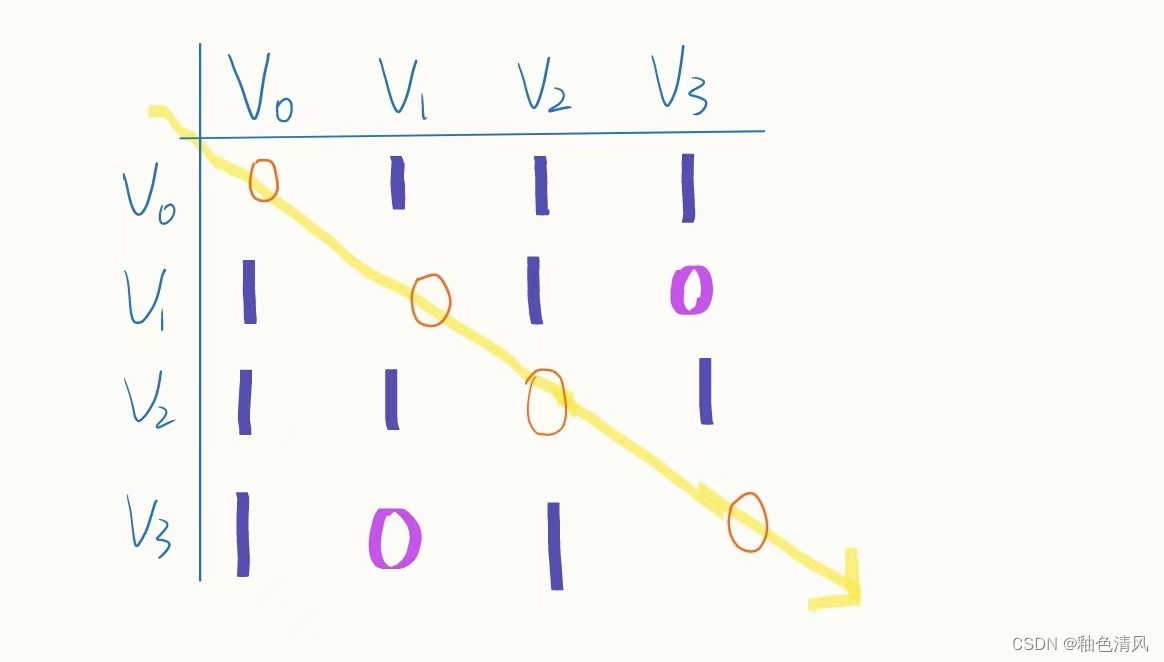
所以它的邻接矩阵为:
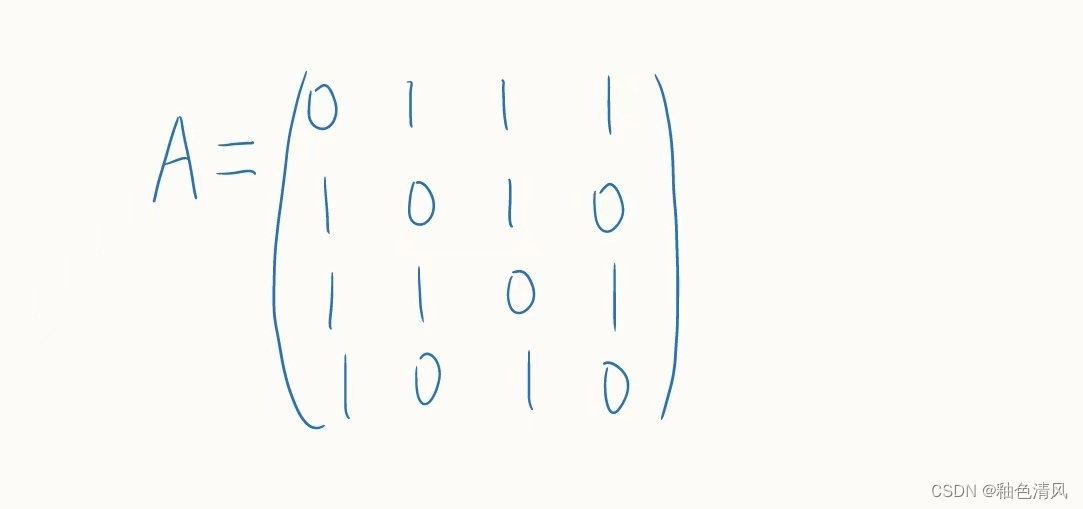
我们可以观察得知,无向图的邻接矩阵是对称的,有向图的邻接矩阵可能是不对称的。

所以它的邻接矩阵为:

邻接矩阵的优点
邻接矩阵的优点在于用邻接矩阵表示图,很容易判定任意两个顶点之间是否有边相连,并求得各个顶点的度数。
对于无向图,顶点vi的度数是邻接矩阵中第i行或第i列值为1的元素个数。
对于有向图,邻接矩阵中第i行值为1的元素个数为顶点vi的出度,第i列值为1的元素的个数为顶点vi的入度。
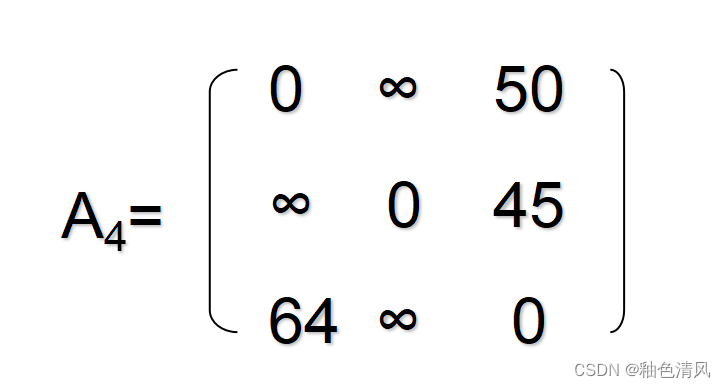
网络的邻接矩阵
当G=(V,E)是一个网络时,G的邻接矩阵是具有如下性质的n阶方阵:

其中Wij表示边上的权值;∞表示一个计算机允许的、大于所有边上权值的数。
下面我们举例说明:
①对于如下这个无向图,求邻接矩阵
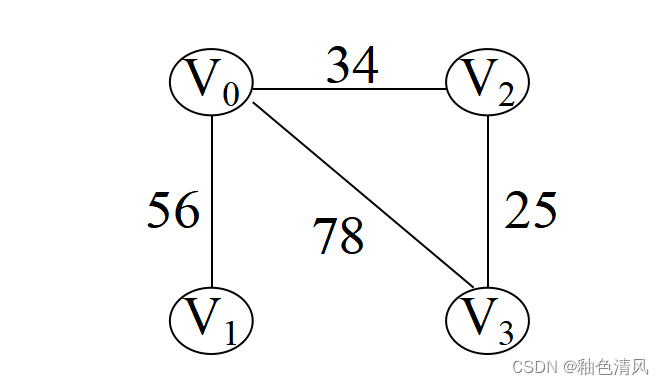
它的邻接矩阵为:

②对于如下这个有向图,求邻接矩阵
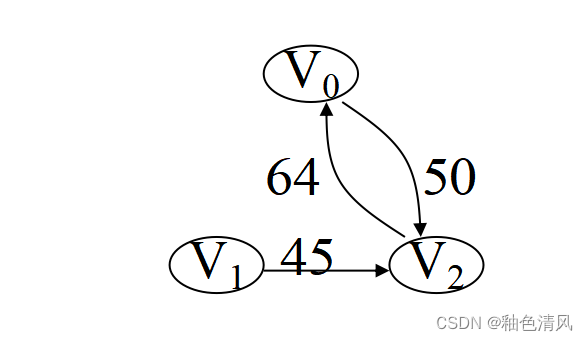
它的邻接矩阵为:
邻接表
如上可以知道,邻接矩阵可以直观地看出一个顶点和另一个顶点之间的关联关系。
但是,邻接矩阵的缺点时什么呢?就是占用太多空间了。
举个例子来说,如果有100个顶点,这100个顶点之间只有10个顶点之间有关联关系,那么就需要建立一个100×100的矩阵,在这个邻接矩阵中,就只有10或20个1,其余都是0,这样的矩阵也叫做 稀疏矩阵,太浪费存储空间了。
所以,为了解决邻接矩阵占用空间的问题,人们想到了另一中种图的表示方法:邻接表。
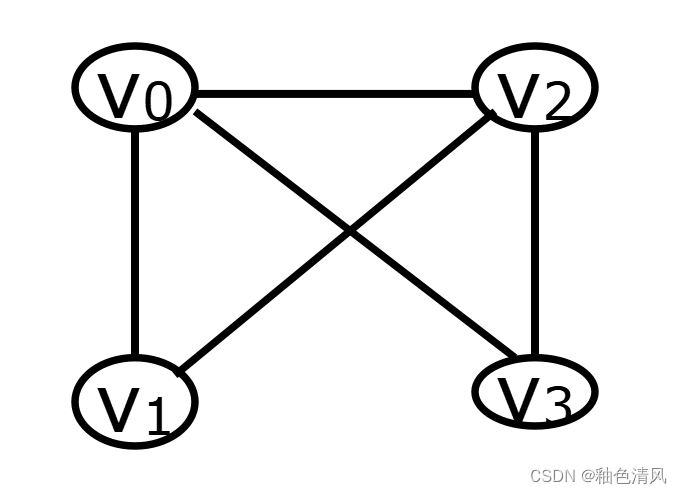
无向图的邻接表
对于图G中的每个顶点vi,该方法把所有邻接于vi的顶点vj链成一个带头结点的单链表,这个单链表就称为顶点vi的邻接表。
单链表中的每个结点至少包含两个域,一个为邻接点域(adjvex),它指示与顶点vi邻接的顶点在图中的位序,另一个为链域(next),它指示与顶点vi邻接的下一个结点。
如下图所示:
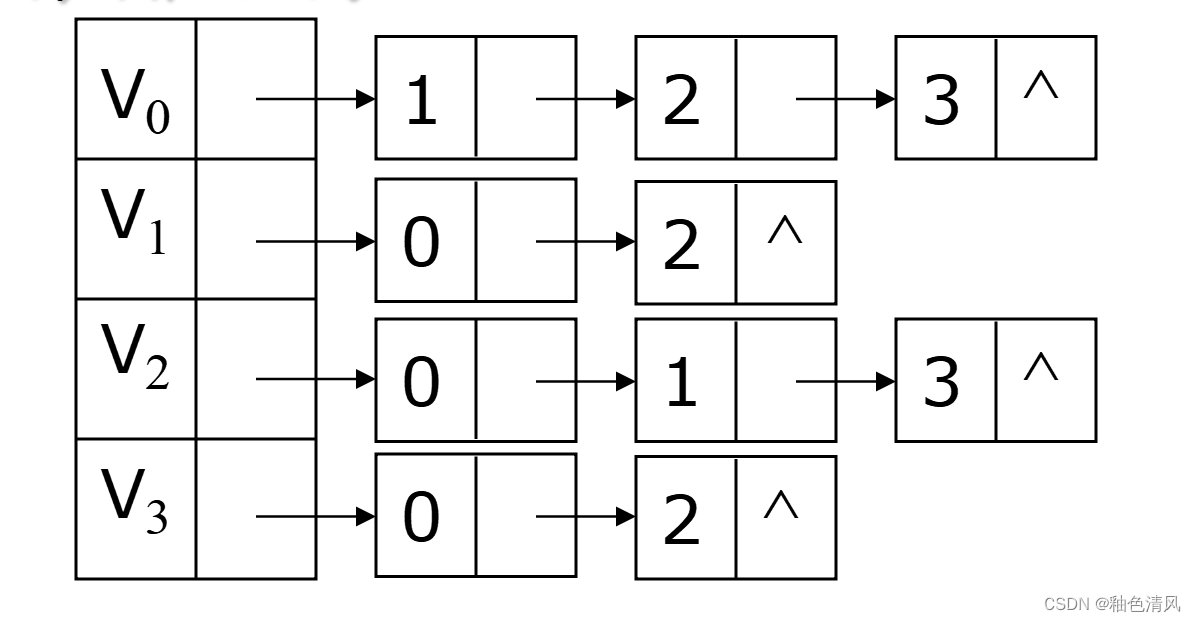
简单理解单链表的组成:
其实,可以将图的单链表理解成由一个又一个“带头结点的单链表”组成的。
当然,严谨来说,肯定不是单链表。这是因为它的表头结点结构和边表结点的结构不同。

它的邻接表为:
有向图的邻接表
对于有向图来说,如果每一顶点vi的邻接表中每个表结点都存储以vi的为始点射出的一条边,则称这种表为有向图的出边表(有向图的邻接表),反之,若每一顶点vi的邻接表中每个表结点都对应于以vi为终点的边(即射入vi的边),则称这种表为有向图的入边表(又称逆邻接表)。
举例如下图所示:
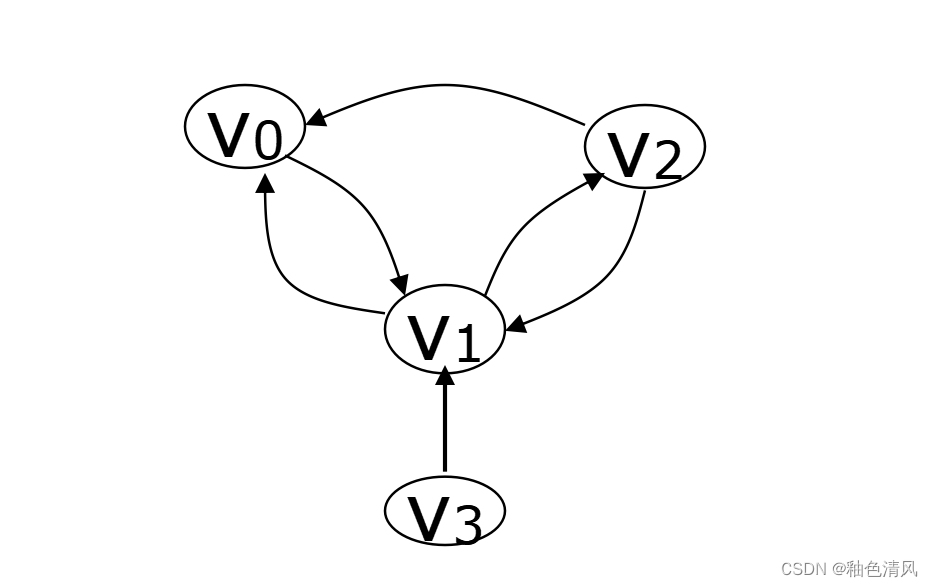
它的出边表:

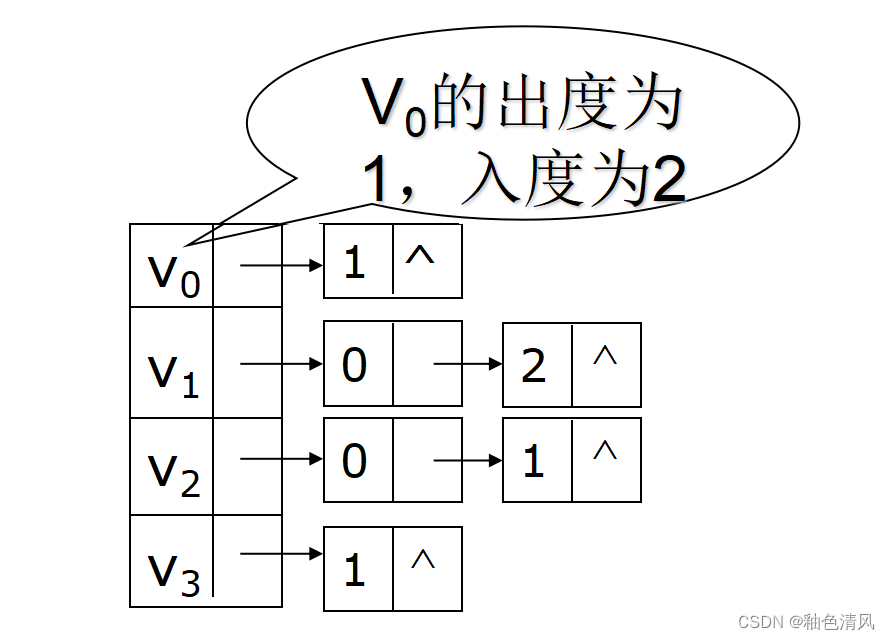
关于顶点的度、出度与入度
在无向图的邻接表中,顶点vi的度为第i个链表中结点的个数;而在有向图的出边表中,第i个链表中的结点个数是顶点vi的出度;为了求入度,必须对整个邻接表扫描一遍,所有链表中其邻接点域的值为i的结点的个数是顶点vi的入度。
若如下图所示已知该图是无向图,则可知,改图种V0的度为3.

若如下图所示,已知改图是有向图,则可知 V0的出度为1,V0的入度为2。
相关文章:

【数据结构】图<简单认识图>
对于下面的内容,大家着重观察和理解图即可,可以直接绕过一些文字性的概念,对图有一个大概的认识。 图 简单认识图图的定义有向图和无向图完全图无向完全图有向完全图 图的基本存储结构邻接矩阵存储邻接矩阵的优点 网络的邻接矩阵邻接表无向图…...

Git介绍和基础命令解析
Git基本操作指令 工作区和暂存区 Git管理的文件分为:工作区(本地的文件夹),版本库(.git文件夹),版本库又分为暂存区stage和暂存区分支master(仓库) 工作区>>>>暂存区>>>>仓库 git add把文件从工作区>>>…...
力扣hot100 和为 K 的子数组 前缀和
👨🏫 题目地址 🍻 AC code class Solution {public int subarraySum(int[] nums, int k){int ans 0;int n nums.length;int[] s new int[n 1];// 前缀和s[0] 0;s[1] nums[0];for (int i 2; i < n; i)s[i] s[i - 1] nums[i - 1…...
6.12找树左下角的值(LC513-M)
算法: 这道题适合用迭代法,层序遍历:按层遍历,每次把每层最左边的值保存、更新到result里面。 看看Java怎么实现层序遍历的(用队列): /*** Definition for a binary tree node.* public clas…...
【精选】框架初探篇之——MyBatis的CRUD及配置文件
MyBatis增删改查 MyBatis新增 新增用户 持久层接口添加方法 void add(User user);映射文件添加标签 <insert id"add" parameterType"com.mybatis.pojo.User">insert into user(username,sex,address) values(# {username},# {sex},# {address}) <…...

ES8语法async与await
async和await两种语法结合可以让异步代码像同步代码一样。 一、async函数 async函数的返回值为Promise对象promise对象的结果由async函数执行的返回值决定 async function fn() {// 返回一个字符串return 字符串;// 返回的结果不是一个Promise类型的对象…...

c#处理SQLSERVER 中image数量类型为空
项目场景: DataRow dataRow dataTable.Rows[i]; var pxpicture dataRow ["pxImage"];if (pxpicture!null){byte[] pic (byte[])pxpicture;acs.Add("pxpicture", Convert.ToBase64String(pic));}问题描述 代码执行出现错误: 无…...

五子棋游戏
import pygame #导入pygame模块 pygame.init()#初始化 screen pygame.display.set_mode((750,750))#设置游戏屏幕大小 running True#建立一个事件 while running:#事件运行for event in pygame.event.get():if event.type pygame.QUIT:#当点击事件后退出running False #事…...
vue+SpringBoot的图片上传
前端VUE的代码实现 直接粘贴过来element-UI的组件实现 <el-uploadclass"avatar-uploader"action"/uploadAvatar" //这个action的值是服务端的路径,其他不用改:show-file-list"false":on-success"handleAvatarSuccess"…...
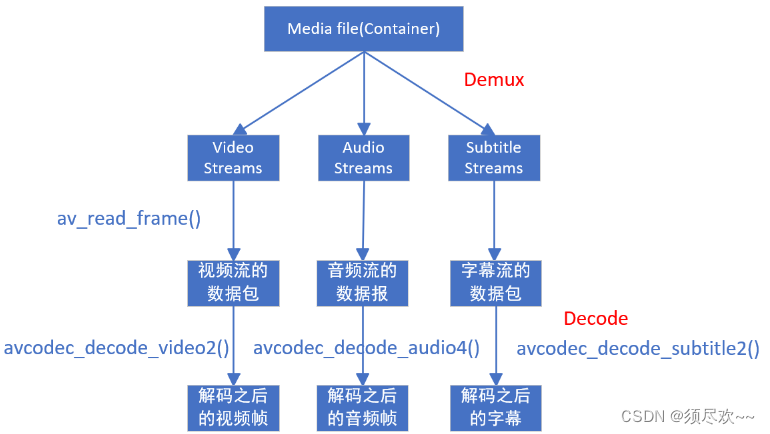
FFmepg 核心开发库及重要数据结构与API
文章目录 前言一、FFmpeg 核心开发库二、FFmpeg 重要数据结构与 API1、简介2、FFmpeg 解码流程①、FFmpeg2.x 解码流程②、FFmpeg4.x 解码流程 3、FFMpeg 中比较重要的函数以及数据结构①、数据结构②、初始化函数③、音视频解码函数④、文件操作⑤、其他函数 三、FFmpeg 流程1…...

训练 CNN 对 CIFAR-10 数据中的图像进行分类
1. 加载 CIFAR-10 数据库 import keras from keras.datasets import cifar10# 加载预先处理的训练数据和测试数据 (x_train, y_train), (x_test, y_test) cifar10.load_data() 2. 可视化前 24 个训练图像 import numpy as np import matplotlib.pyplot as plt %matplotlib …...

香港科技大学广州|智能制造学域博士招生宣讲会—天津大学专场
时间:2023年12月07日(星期四)15:30 地点:天津大学卫津路校区26楼B112 报名链接:https://www.wjx.top/vm/mmukLPC.aspx# 宣讲嘉宾: 汤凯教授 学域主任 https://facultyprofiles.hkust-gz.edu.cn/faculty-p…...
— 子数组中满足max -min <= sum的个数)
滑动窗口练习(二)— 子数组中满足max -min <= sum的个数
题目 给定一个整型数组arr,和一个整数num 某个arr中的子数组sub,如果想达标,必须满足: sub中最大值 – sub中最小值 < num, 返回arr中达标子数组的数量 暴力对数器 暴力对数器方法主要是用来和另一个方法互相校验正…...

用xlwings新建一个excel并同时生成多个sheet
新建一个excel并同时生成多个sheet,要实现如下效果: 一般要使用数据透视表来快速实现。 今天记录用xlwings新建一个excel并同时生成多个sheet。 import xlwings as xw # 打开excel,参数visible表示处理过程是否可视,add_book表示是否打开新的Excel程序…...

诺威信,浪潮云,微众区块链
目录 诺威信B隐私计算平台 浪潮云=星火连-澳优码 HyperChain 产品介绍 CA认证即电子认证服务...

Redux在React中的使用
Redux在React中的使用 1.构建方式 采用reduxjs/toolkitreact-redux的方式 安装方式 npm install reduxjs/toolkit react-redux2.使用 ①创建目录 创建store文件夹,然后创建index和对应的模块,如上图所示 ②编写counterStore.js 文章以counterStore…...
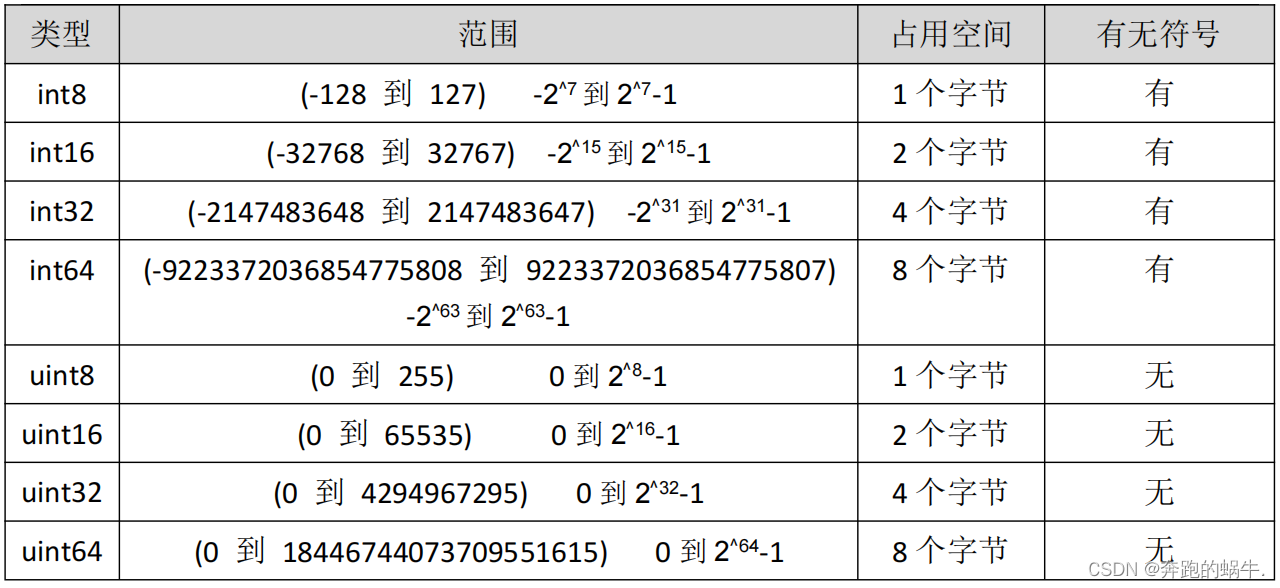
Go 数字类型
一、数字类型 1、Golang 数据类型介绍 Go 语言中数据类型分为:基本数据类型和复合数据类型基本数据类型有: 整型、浮点型、布尔型、字符串复合数据类型有: 数组、切片、结构体、函数、map、通道(channel)、接口 2、…...
时间序列预测 — Informer实现多变量负荷预测(PyTorch)
目录 1 实验数据集 2 如何运行自己的数据集 3 报错分析 1 实验数据集 实验数据集采用数据集4:2016年电工数学建模竞赛负荷预测数据集(下载链接),数据集包含日期、最高温度℃ 、最低温度℃、平均温度℃ 、相对湿度(平均) 、降雨…...

2023年金融信创行业研究报告
第一章 行业概况 1.1 定义 金融信创是指在金融行业中应用的信息技术,特别是那些涉及到金融IT基础设施、基础软件、应用软件和信息安全等方面的技术和产品。这一概念源于更广泛的“信创 (信息技术应用创新)”,即通过中国国产信息技术替换海外信息技术&a…...

51单片机按键控制LED灯亮灭的N个玩法
51单片机按键控制LED灯亮灭的N个玩法 1.概述 这篇文章介绍按键的使用,以及通过控制LED灯的小实验,发现按键中存在的问题,然后思考并解决这些问题。达到熟练使用按键控制元器件。 2.搭建硬件环境 1.硬件准备 名称型号数量单片机STC12C205…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
