关键路径-STL版/拓扑排序 关键路径【数据结构】
关键路径-STL版
题目描述
给定有向图无环的边信息,求每个顶点的最早开始时间、最迟开始时间。
输入
第一行图的顶点总数
第二行边的总数
第三行开始,每条边的时间长度,格式为源结点 目的结点 长度
输出
第一行:第个顶点的最早开始时间
第二行:每个顶点的最迟开始时间
输入样例1
9
12
0 1 3
0 2 10
1 3 9
1 4 13
2 4 12
2 5 7
3 6 8
3 7 4
4 7 6
5 7 11
6 8 2
7 8 5
输出样例1
0 3 10 12 22 17 20 28 33
0 9 10 23 22 17 31 28 33
拓扑排序 关键路径
拓扑排序其实就是对有向无环图的顶点的一种排序,每个顶点出现且只出现一次。
对一个AOV网进行拓扑排序的方法:
- 从AOV网中选择一个入度为0的顶点并输出;
- 从网中删除该顶点和所有以它为起点的有向边;
- 重复1和2直到当前的AOV网为空或当前网中不存在入度为0的顶点为止;
- 拓扑排序可以验证是否有环,如果有环,则无法将所有节点加入排序数组,如果没环就可以
- 拓扑排序序列不是唯一的,可以根据节点序号递增,或通过队列、栈来给出
- 逆拓扑排序也可以是拓扑排序逆过来
逆拓扑排序的步骤:
1、从AOV网中选择一个出度为0的顶点并输出;
2、从网中删除该顶点和所有以它为终点的有向边;
3、重复1和2,直到当前的AOV网为空
关键路径:从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
- 活动ai的最早开始时间e(i):指该活动弧的起点所表示的事件的最早发生时间;
- 活动ai的最迟开始时间l(i):指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差;
- 活动ai的时间余量:d(i)=l(i)-e(i),表示在不增加完成整个工程所
- l(i)=e(i)的活动ai是关键活动,由关键活动组成的路径就是关键路径。
#include<bits/stdc++.h>
using namespace std;
int main()
{int n;cin>>n;int line;cin>>line;//邻接矩阵int a[505][505] = {0};//顶点入度int ind[505] = {0};for(int i = 0; i < line; i++){int v1,v2,v;cin>>v1>>v2>>v;a[v1][v2] = v;ind[v2] ++;}queue<int> q;//拓扑排序数组int ssort[505];for(int i = 0; i < n; i++){if(ind[i] == 0) {q.push(i);ind[i] = -1;}}int cnt = 0;while(!q.empty()){int now = q.front();q.pop();//加入拓扑排序数组ssort[cnt++] = now;for(int i = 0; i < n; i++){if(a[now][i]) ind[i]--;if(ind[i] == 0){q.push(i);ind[i] = -1;}}}//拓扑排序另一种实现方式 更方便// int num = 0;// // while(num < n)// {// for(int i = 0; i < n; i++)// {// if(ind[i] == 0) // {// ind[i] = -1;// ssort[num++] = i;// for(int j = 0; j < n; j++)// {// if(a[i][j]) ind[j]--;// }// }// }// }int start = ssort[0];int end = ssort[n-1];//最早开始时间和最晚开始时间int earliest[505] = {-1}, latest[505] = {99999999};earliest[start] = 0;//最早开始时间根据拓扑排序顺序计算//即前一个的最早开始时间加上到该点的时间的最大值for(int i = 1; i < n; i++){int ans = 0;int index = ssort[i];for(int j = 0; j < n; j++){if(a[j][index]) ans = max(ans,earliest[j] + a[j][index]);}earliest[index] = ans;}for(int i = 0; i < n; i++){cout<<earliest[i]<<" ";}cout<<endl;//最后一个点的最早开始时间和最晚开始时间相等latest[end] = earliest[end];//最晚开始时间根据逆拓扑排序顺序计算//即后一个点的最晚开始时间减去到该点的时间的最小值for(int i = n-2; i >= 0; i--){int index = ssort[i];int ans = 99999999;for(int j = 0; j < n; j++){if(a[index][j]) ans = min(ans,latest[j] - a[index][j]);}latest[index] = ans;}for(int i = 0; i < n; i++){cout<<latest[i]<<" ";}cout<<endl;return 0;
}
另外可以用DFS求拓扑排序数组:
祖先结点的DFS函数结束时间大于子孙结点的DFS函数结束时间,利用DFS求出各顶点结束时间,对于拓扑排序,就是将结束时间从大到小排序。
相关文章:

关键路径-STL版/拓扑排序 关键路径【数据结构】
关键路径-STL版 题目描述 给定有向图无环的边信息,求每个顶点的最早开始时间、最迟开始时间。 输入 第一行图的顶点总数 第二行边的总数 第三行开始,每条边的时间长度,格式为源结点 目的结点 长度 输出 第一行:第个顶点的最早…...
最新AI创作系统ChatGPT系统运营源码,支持GPT-4图片对话能力,上传图片并识图理解对话,支持DALL-E3文生图
一、AI创作系统 SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧!本系统使用NestjsVueTypescript框架技术,持续集成AI能力到本系统。支持OpenAI DALL-E3文生图,…...

小航助学题库蓝桥杯题库stem选拔赛(21年3月)(含题库教师学生账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSDN博客 需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSD…...
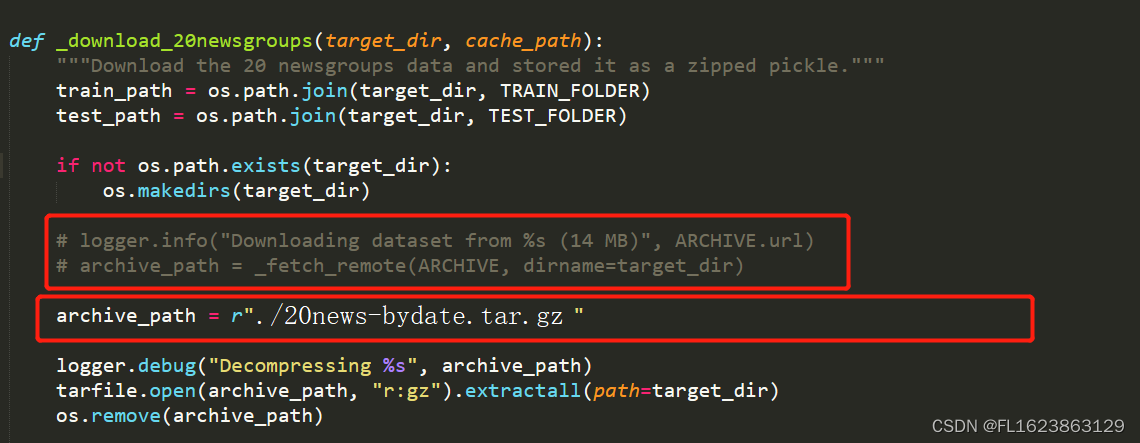
[python]离线加载fetch_20newsgroups数据集
首先手动下载这个数据包 http://qwone.com/~jason/20Newsgroups/20news-bydate.tar.gz 下载这个文件后和脚本放一起就行,然后 打开twenty_newsgroups.py文件(在fetch_20newsgroups函数名上,右键转到定义即可找到) 之后运行代码即…...

Python与设计模式--代理模式
5-Python与设计模式–代理模式 一、网络服务器配置白名单 代理模式是一种使用频率非常高的模式,在多个著名的开源软件和当前多个著名的互联网产品后 台程序中都有所应用。下面我们用一个抽象化的简单例子,来说明代理模式。首先,构造一个网…...

ubuntu挂载磁盘,以及开机自动挂载磁盘
1. 挂载临时磁盘(关机自动取消挂载) 在Ubuntu上挂载磁盘涉及到几个步骤,其中包括查看可用磁盘、创建挂载点、编辑 /etc/fstab 文件以确保在系统启动时自动挂载等。以下是一般的步骤: **查看可用磁盘和分区:**可以使用…...
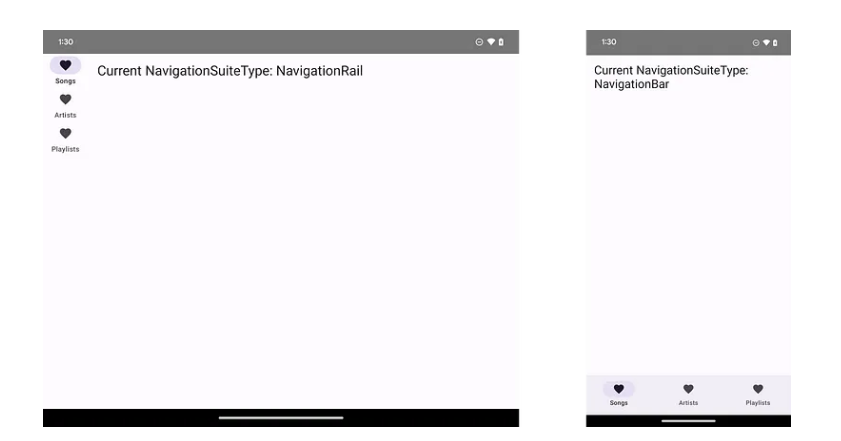
Jetpack Compose中适应性布局的新API
Jetpack Compose中适应性布局的新API 针对大屏幕优化的新组合件。 使用新的Material适应性布局,为手机、可折叠设备和平板电脑构建应用程序变得更加简单!市场上各种不同尺寸的Android设备的存在挑战了构建应用程序时对屏幕尺寸的通常假设。开发者不应该…...

小航助学题库蓝桥杯题库stem选拔赛(22年1月)(含题库教师学生账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSDN博客 需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)_程序猿下山的博客-CSD…...

蓝桥杯第100 题 九宫幻方 DFS 全排列 C++ 解题思维
题目 九宫幻方https://www.lanqiao.cn/problems/100/learning/?page1&first_category_id1&name%E4%B9%9D 思路和解题方法 一 (DFS) 首先,定义了一些全局变量和数组。vis数组用于标记已经出现过的数字,a数组用于存储数独的初始状态…...

NOI / 1.10编程基础之简单排序 提问05:分数线划定 c语言 结构体
描述 世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的150%划定,即如果计划录取m名志愿者,则面试…...

再探Docker:从Docker基础到跨服务器部署
摘要: 这篇文章将从介绍Docker基础开始,逐步讲解如何创建镜像、使用Docker Compose编排容器、在Docker中更新部署环境,将更新后的环境打包为镜像并导出为tar包,最后在其他服务器上应用这个镜像。 1. Docker是什么 Docker是一种容…...
C# 使用PanGu分词
写在前面 这是官方介绍:盘古分词是一个中英文分词组件。作者eaglet 曾经开发过KTDictSeg 中文分词组件,拥有大量用户。作者基于之前分词组件的开发经验,结合最新的开发技术重新编写了盘古分词组件。 盘古分词组件需要配合其字典文件使用&am…...
Termius 一款优秀的跨平台 SSH 客户端工具
🔥🔥🔥 作为程序员或者运维管理人员,我们经常需要使用终端工具来进行服务器管理及各种操作,比如部署项目、调试代码、查看/优化服务、管理服务器等。 而实现远程服务器连接需要借助 SSH 协议来进行,SSH&am…...
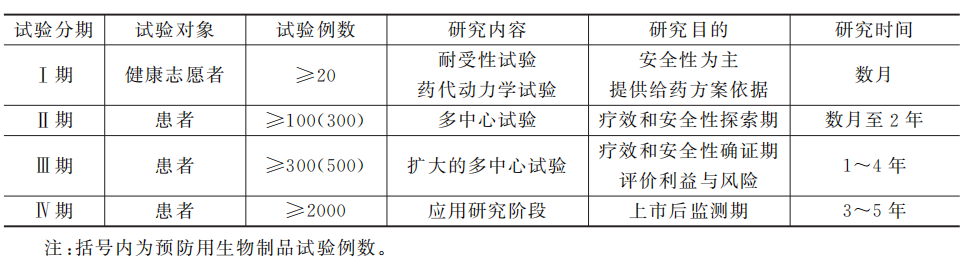
生命科学领域 - 新药从研发到上市全流程
新药是指新研制的、临床尚未应用的药物,其化学本质应为新的化合物或称新化学实体、 新 分子实体、新活性实体。新药研发的根本目的是治疗疑难危重疾病,研制出来的药物即使是全新的化学结构,但是疗效或安全性却不及现有的药物便失去新药价值&a…...
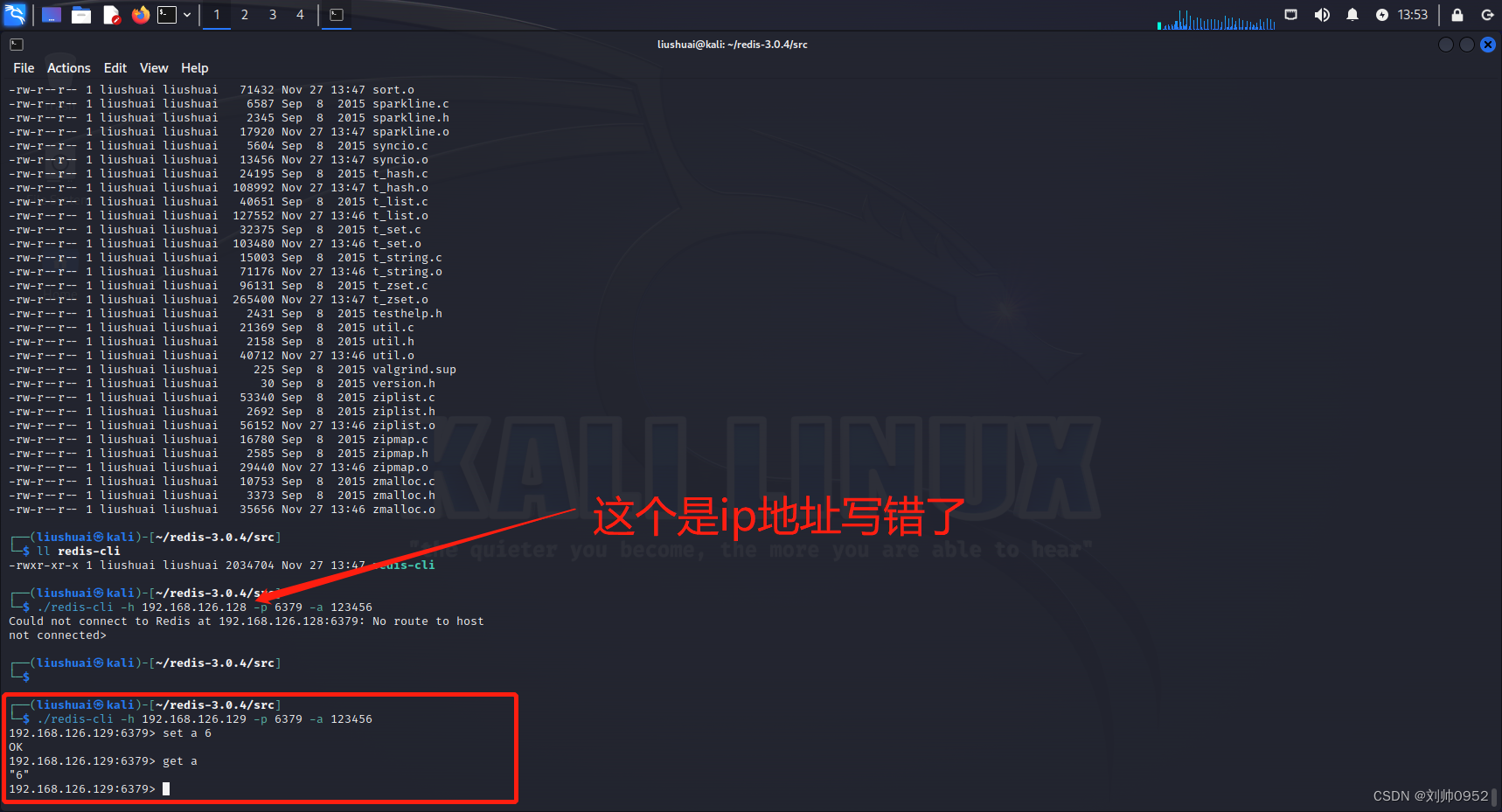
血的教训------入侵redis之利用python来破解redis密码
血的教训------入侵redis之利用python来破解redis密码 利用强大的python来进行redis的密码破解,过程不亦乐乎,当然也可以用shell脚本 本篇文章只供学习交流,请勿他用,谢谢。 其他相关联的文章 [1]VMware安装部署kail镜像服务器【…...

yolov8-pose 推理流程
目录 一、关键点预测 二、图像预处理 二、推理 三、后处理与可视化 3.1、后处理 3.2、特征点可视化 四、完整pytorch代码 yolov8-pose tensorrt 一、关键点预测 注:本篇只是阐述推理流程,tensorrt实现后续跟进。 yolov8-pose的tensorrt部署代码…...

笔记十七、认识React的路由插件react-router-dom和基本使用
react-router 分类 web使用 react-router-dom native使用 react-router-native anywhere(使用麻烦) react-router 安装 yarn add react-router-dom main.jsx import React from "react"; import ReactDOM from "react-dom/client"…...

CleanMyMac X4.14.5Crack最新Mac电脑清理优化最佳应用
CleanMyMac X 4.14.5是用于清理和优化Mac的最佳应用程序和强大工具。它看起来很棒而且很容易理解。该软件可以清理、保护、优化、稳定和维护您的 Mac 系统。您可以立即删除不必要的、不寻常的、无用的垃圾文件、损坏的文件垃圾,并释放大量内存空间。此外,…...

Linux shell单双引号区别
shell单双引号区别: Shell脚本中很多时候都在用单引号或双引号来框住字符串,但是他们之间是存在区别的 避免踩坑记录… 单引号 单引号中的任何字符都没有特殊含义,即一些转义字符,$ 变量引用都会无效,它只把他们当作一个单纯的…...
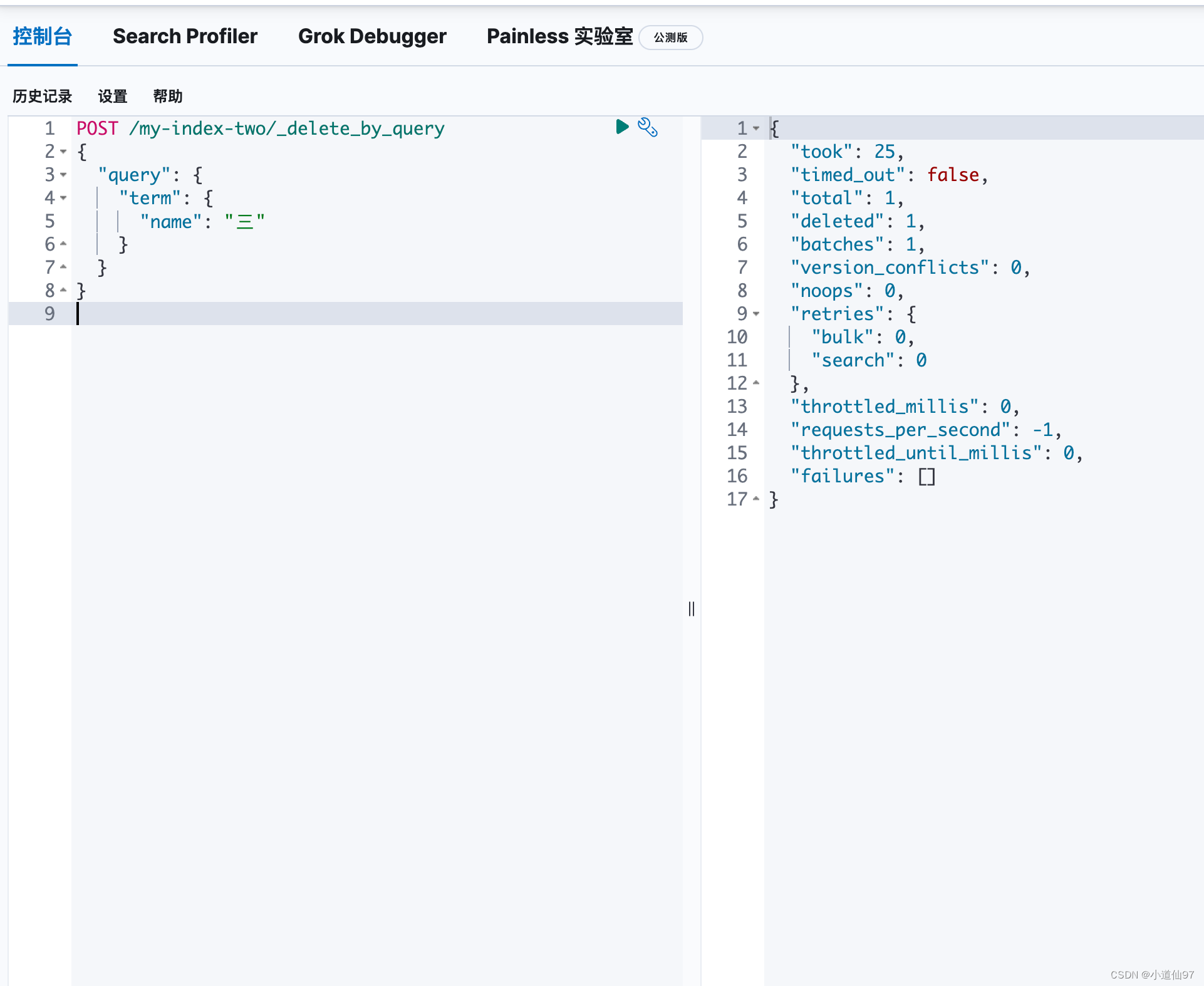
ES 8.x开始(docker-compose安装、kibana使用、java操作)
学习文档地址 一、Docker安装 这里使用docker-compose来安装,方便后续迁移,Elasticserach和kibina一起安装。 1、创建安装目录 configdataplugins 2、配置文件 配置文件有两个,一个是ES的配置文件,一个docker-compose的配置文件 …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
