[Java·算法·中等]LeetCode17. 电话号码的字母组合
每天一题,防止痴呆
- 题目
- 示例
- 分析思路1
- 题解1
- 分析思路2
- 题解2
题目
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
输入:digits = ""
输出:[]
输入:digits = "2"
输出:["a","b","c"]
分析思路1
可以使用递归的方式来实现。
使用了一个数组来保存数字与字母的对应关系。在递归过程中,我们不断地向已有的组合中添加新的字母,直到所有数字都被处理完毕。
题解1
class Solution {// 定义数组存储每个数字对应的字母,下标0和1均为空private final String [] arr = new String[]{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};public List<String> letterCombinations(String digits) {List<String> res = new ArrayList<>();if(digits == null || digits.length() == 0){return res;}backtrack(digits, 0, "", res);return res;}private void backtrack(String digits, int index, String combination, List<String> res){if(index == digits.length()){res.add(combination);return;}// 利用char变量使用 ASCII进行算术运算这一特征,可以得到一种间接计算获取数值的方法// '0'-'9' ASCII 为 48-57,且顺序一致,因而char数字之间的差值等于数字之间的差值String letters = arr[digits.charAt(index) - '0'];for(int i = 0; i < letters.length(); i++){backtrack(digits, index + 1, combination + letters.charAt(i), res);}}
}
执行结果
分析思路2
使用回溯算法进行求解。
首先,定义一个哈希表,将每个数字对应的字母存入其中,以便后续查找。
然后,定义一个结果列表 res,用于存储所有的字母组合。
接着,调用回溯函数 backtrack,该函数的参数为当前要处理的电话号码字符串 digits、当前要处理的字符索引 index、当前已经组合好的字母字符串 combination 和结果列表 res。
在回溯函数中,首先判断当前要处理的字符索引是否等于电话号码字符串的长度,如果是,说明已经处理完了所有的字符,此时将当前已经组合好的字母字符串 combination 添加到结果列表 res 中,并返回。
如果当前要处理的字符索引小于电话号码字符串的长度,说明还有字符需要处理。首先从哈希表中获取当前数字对应的字母列表 letters,然后依次枚举其中的每个字母,并将其添加到当前已经组合好的字母字符串 combination 的末尾,然后递归调用回溯函数 backtrack,处理下一个字符。
在递归返回后,需要将当前已经组合好的字母字符串 combination 的末尾字符删除,以便后续枚举其他字母。
题解2
class Solution {private Map<Character, String> phone = new HashMap<Character, String>() {{put('2', "abc");put('3', "def");put('4', "ghi");put('5', "jkl");put('6', "mno");put('7', "pqrs");put('8', "tuv");put('9', "wxyz");}};public List<String> letterCombinations(String digits) {List<String> res = new ArrayList<String>();if (digits.length() == 0) {return res;}backtrack(digits, 0, new StringBuilder(), res);return res;}private void backtrack(String digits, int index, StringBuilder combination, List<String> res) {if (index == digits.length()) {res.add(combination.toString());return;}char digit = digits.charAt(index);String letters = phone.get(digit);for (int i = 0; i < letters.length(); i++) {combination.append(letters.charAt(i));backtrack(digits, index + 1, combination, res);combination.deleteCharAt(index);}}
}执行结果
相关文章:

[Java·算法·中等]LeetCode17. 电话号码的字母组合
每天一题,防止痴呆题目示例分析思路1题解1分析思路2题解2题目 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。…...

C#7/C#8/C#9 与dotnetSDK 以及dotnet framework对应关系
语言版本 对应的.net framework版本 对应的.net sdk版本 推荐使用的vs studio C#7.3 3.5、 4.0、 4.5 、4.5.1、 4.5.2 、4.6 、4.6.1、 4.6.2 4.7.1、 4.7.2 .netcore 2.0、.netcore2.1、 .netcore2.2 C#8.0 / F#4.7 不支持 .netcore 3.0、.netcore 3.1 C# 9.0 …...

jvm调优经验总结
最近一段时间很忙,忙到每天10点多11点下班还是感觉有很多事没有做完,不过倒也没有什么太过低落的情绪,有时候只安静的看一个视频,简单看点文字,或者平静的坐着,并没有太多想法。短时间的工作压力是可以接受…...

等保合规知识常见问题解答
Q1:什么是等级保护? 答:等级保护是指对国家重要信息、法人和其他组织及公民的专有信息以及公开信息和存储、传输、处理这些信息的信息系统分等级实行安全保护,对信息系统中使用的信息安全产品实行按等级管理,对信息系统…...

分享5款Windows同类软件中的翘楚
今天要给大家推荐的是5款软件,每个都是同类软件中的个中翘楚,请大家给我高调地使用起来,不用替我藏着掖着。1.沙盒工具——Sandboxie Sandboxie是一个电脑必备的沙盘工具,对于从网上下载的软件安装包、文件、视频、图片等等一切不…...

记--springboot-工具类中使用@Component、@Resource与@Value失效
写一个工具类 需要使用Resource注入RedisTemplate 使用Value获取application.properties配置文件中配置 并使用Component将该工具类交个spring管理 调试的时候RedisTemplate以及所有的变量全是是null 看了网上的各种解决方式五花八门 有的说出现问题的原因:Compon…...

手写一个react,看透react运行机制
适合人群 本文适合0.5~3年的react开发人员的进阶。 讲讲废话: react的源码,的确是比vue的难度要深一些,本文也是针对初中级,本意让博友们了解整个react的执行过程。 写源码之前的必备知识点 JSX 首先我们需要了解什么是JSX。…...

JS判断输入值是否为正整数,判断变量是否为数字
这篇文章将讨论如何确定一个变量是否代表 JavaScript 中的有效数字。 1.JS中的test是原来是JS中检测字符串中是否存在的一种模式,JS输入值是否为判断正整数代码: <script type”text/javascript”> function test() { var num document.getElem…...

Android开发八股文,Android也有自己的八股文了
前言别的行业都有自己的八股文,凭什么Android没有。2023春招即将来临,很多同学会问 Android开发的面试题有必要背吗?我的回答是:很有必要。你可以讨厌这种模式,但你一定要去背,因为不背你就进不了大厂。国内…...
你需要同款“Unreal项目自动化编译、打包和部署”方案吗?
在过往几期的UWA Pipeline最佳实践案例中,我们分享了如何通过Pipeline实现性能优化、性能管理、游戏内容验收和云真机系统的应用(实现批量真机设备的自动化测试,以及针对特效性能优化的方式),其实这些高效的方法并不局…...
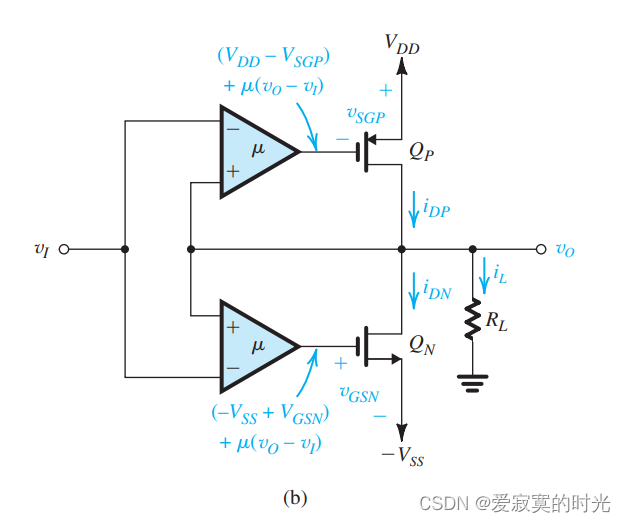
电子技术——CMOS-AB类输出阶
电子技术——CMOS-AB类输出阶 本节我们研究CMOS-AB类输出阶。 经典配置 下图展示了一个经典的CMOS-AB类输出阶: 这个很像BJT二极管偏置版本的AB类输出阶,在这里二极管偏置变成了 Q1Q_1Q1 和 Q2Q_2Q2 偏置。不想BJT的情况,这里 QNQ_NQN…...

2023王道考研数据结构笔记第二章线性表
第二章 线性表 2.1 线性表的定义 2.1.1 线性表的基本概念 线性表是具有相同数据类型的n(n>0)个数据元素的有限序列,其中n为表长,当n0时线性表是一个空表。若用L命名线性表,则其一般表示为: L(a1,a2,...,ai,ai1,...,an)L(a_1…...
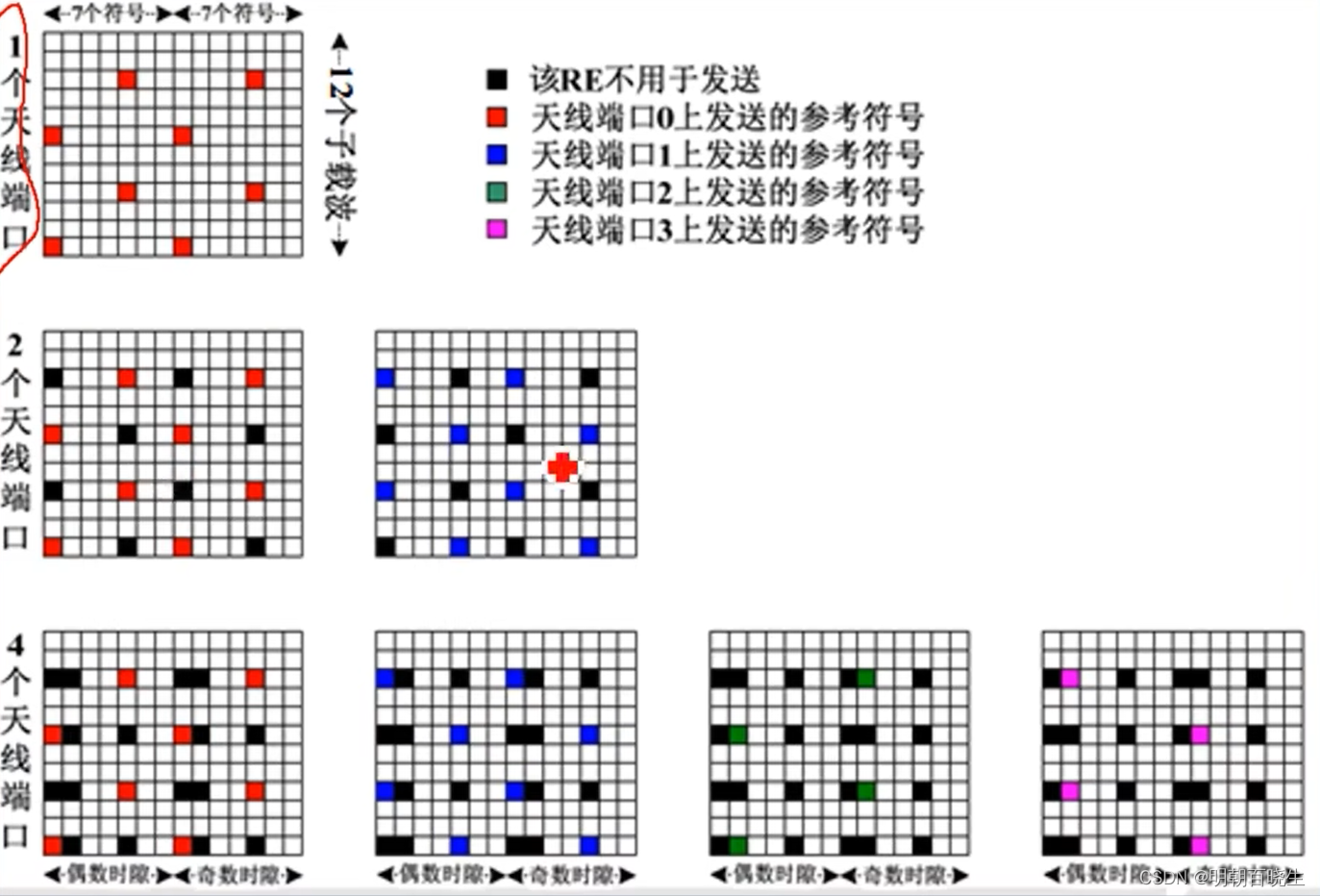
[chapter 11][NR Physical Layer][Layer Mapping]
前言:这里参考Curious Being系列 ,简单介绍一下NR 5G 物理层核心技术层映射.我们主要讲了一下what is layer Mapping, why need layer Mapping, how layer Mapping 参考文档:3GPP 38.211- 6.3.1.3 Layer mapping《5G NR Physical Layer | Cha…...

什么是工业物联网(IIoT)?
什么是工业物联网(IIoT)?工业物联网(IIoT) 被定义为一组设备和应用,允许大企业创建从核心到边缘的端到端连接环境。其还包括传统的物理基础设施,如集装箱和物流卡车,以收集数据,对事件做出反应,并在智能设备的帮助下做…...
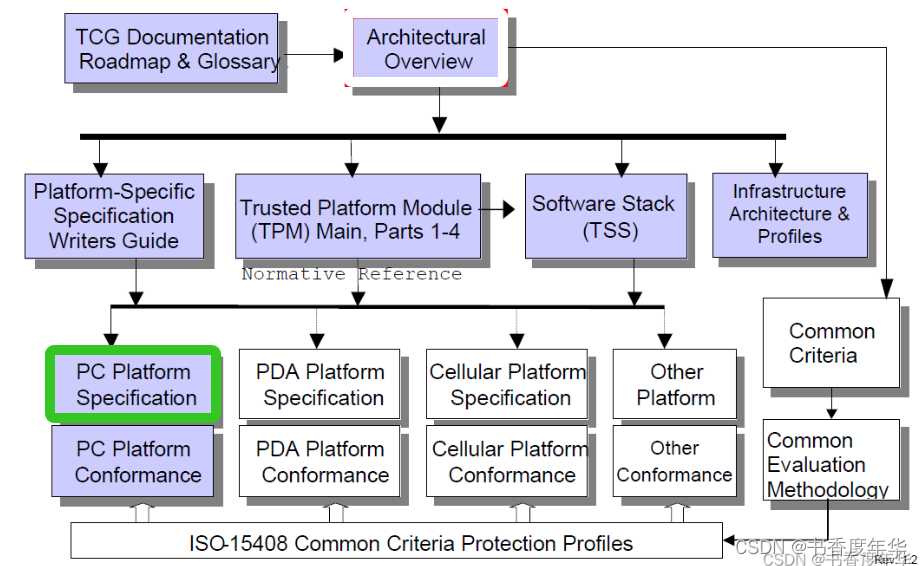
「TCG 规范解读」PC 平台相关规范(4)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

CSS背景属性之颜色渐变
颜色渐变 颜色渐变其实在网页设计中并不是特别常见, 但也不可避免的会出现导航栏是渐变色这种情况或者别的不是单一颜色的情况, 例如:这样的设计解决方案并不是只可以使用颜色渐变,我们可以使用两个div拼接,将文字放…...
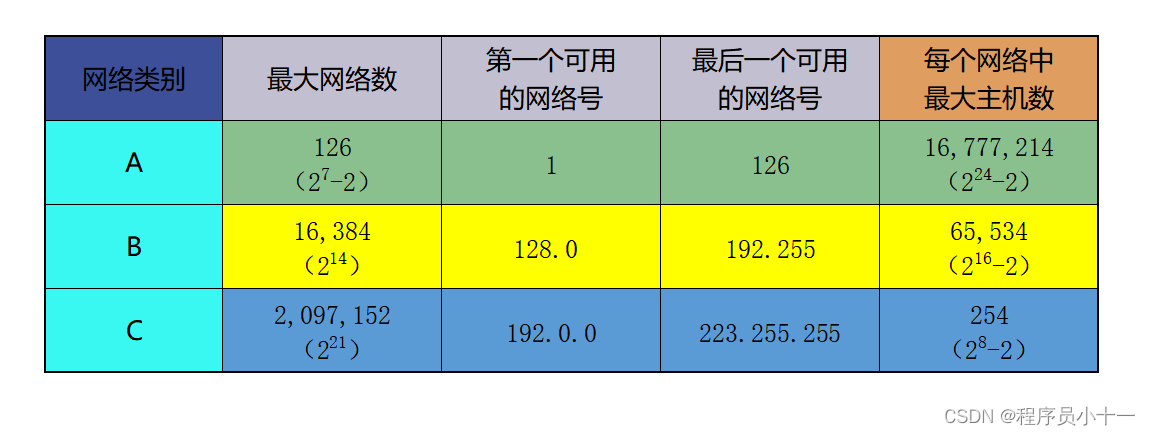
IPv4地址细讲
文章目录一、IPv4地址简介二、IPv4地址的表示方法点分十进制记法三、IP地址的分类四、特殊IPv4地址:全 “0” 和全 “1”五、常用的三类IP地址使用范围六、五类IP地址的范围一、IPv4地址简介 IPv4地址分5类,每一类地址都由固定长度的字段组成࿱…...

sql语句中exists用法详解
文章目录一、语法说明exists:not exists:二、常用示例说明1.查询a表在b表中存在数据2.查询a表在b表中不存在数据3.查询时间最新记录4.exists替代distinct剔除重复数据总结一、语法说明 exists: 括号内子查询sql语句返回结果不为空ÿ…...

思迅软件端口不通导致软件和软锁报错的问题
一、端口不通导致软件和软锁报错的问题 问题说明:打开软件提示到:xxx.xxx.xxx.xxx失败! 处理步骤1: 假设软锁服务器IP为192.168.0.1,分别在服务器本机和客户端电脑测试软锁服务: 在服务器的浏览器中访问地址: http:/…...
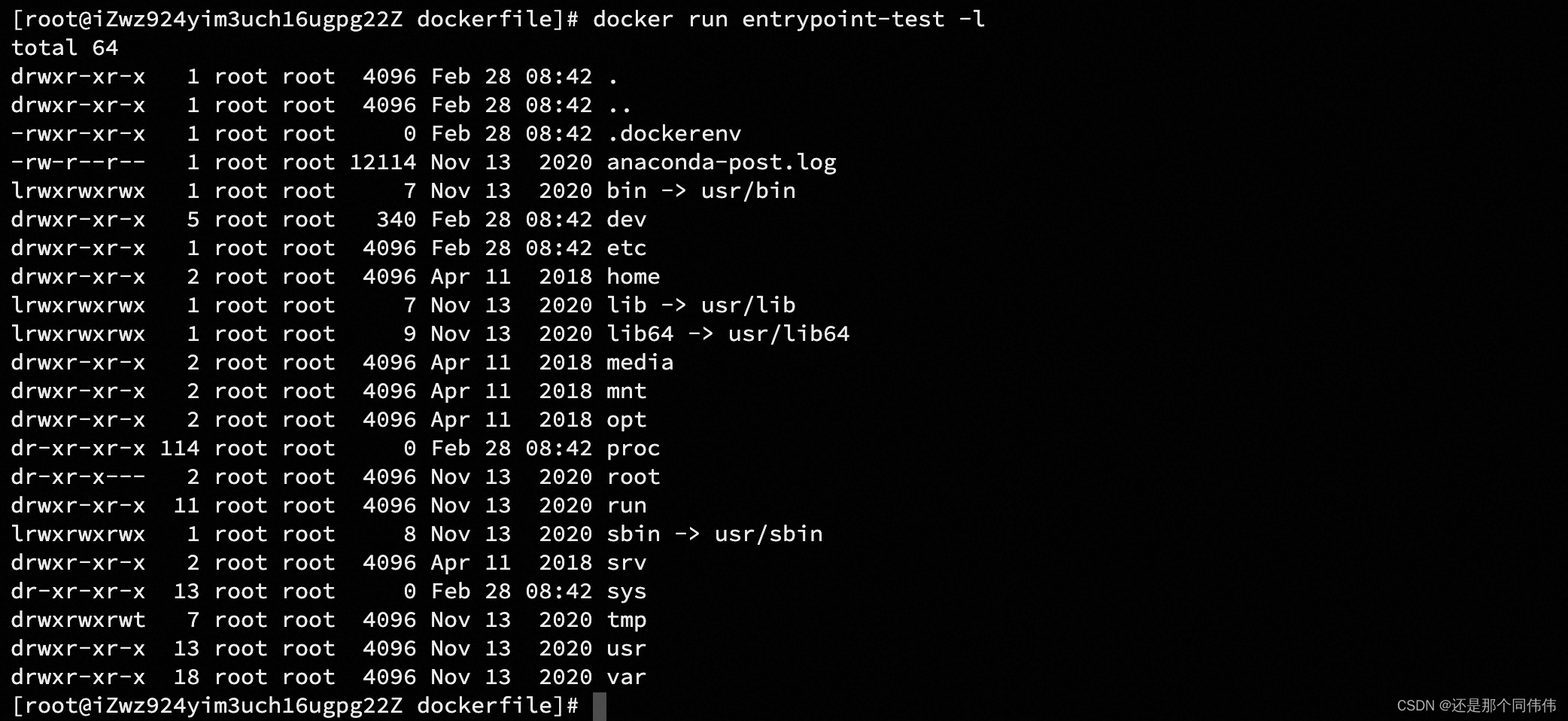
Docker之路(7.DockerFile文件编写、DockerFile 指令解释、CMD与ENTRYPOINT的区别)
1.DockerFile介绍 dockerfile 是用来构建docker镜像的文件!命令参数脚本! 构建步骤: 编写一个dockerfile文件docker build构建成为一个镜像docker run 运行镜像docker push发布镜像(DockerHub、阿里云镜像仓库) 2.Dock…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
