振弦式轴力计和振弦采集仪组成的安全监测解决方案
振弦式轴力计和振弦采集仪组成的安全监测解决方案
振弦式轴力计和振弦采集仪是一种常用的结构安全监测工具,可以用于评估建筑物、桥梁、隧道或其他结构的结构健康状态和安全性能。这种监测方案较为先进、精确,并且能够监测长期的结构反应,因此在工程领域中广泛应用。
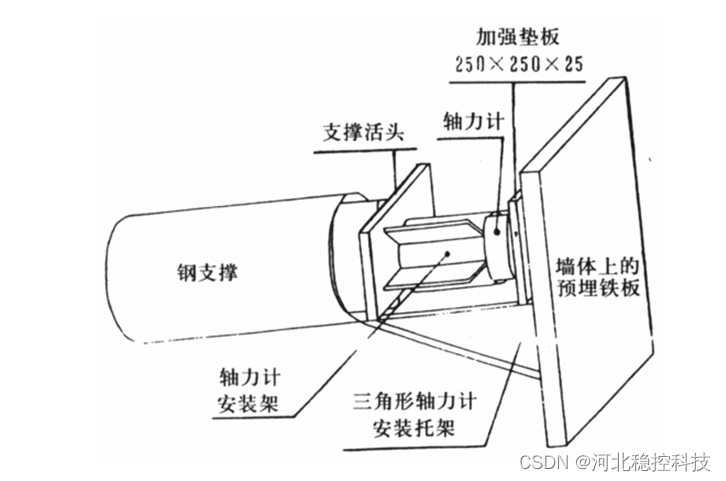
下面是振弦式轴力计和振弦采集仪组成的安全监测解决方案的主要步骤:
1. 选取适合的振弦式轴力计和振弦采集仪,并按照相关产品说明进行组装和安装。振弦式轴力计的使用需要考虑悬挂位置、工作原理和测量范围等因素,振弦采集仪的选用应综合考虑测量频率、采样精度和数据传输方式等因素。
2. 在结构体系中安装振弦式轴力计和振弦采集仪,根据实际情况确定安装位置和数量。在安装过程中,需要保证安装稳定、精度可靠,并注意防水、防雷等安全措施的采取。
3. 启动振弦采集仪,将采集仪与计算机或其他数据存储设备连接,进行数据采集和存储。采集过程中需要注意数据的精度和采集频率,以获取准确的结构参数信息。
4. 对采集的数据进行分析处理,获取结构的反应特征和安全状态,进行结构健康评估和安全性能分析。

5. 根据分析结果进行相应的维护和保养,及时排除结构中的潜在问题,保证结构的安全运行。
需要注意的是,振弦式轴力计和振弦采集仪组成的安全监测解决方案需要专业技术人员进行操作和维护,避免出现误差和安全事故。同时,应遵守相关安全法规和规范,确保监测过程的安全性和可靠性。
相关文章:

振弦式轴力计和振弦采集仪组成的安全监测解决方案
振弦式轴力计和振弦采集仪组成的安全监测解决方案 振弦式轴力计和振弦采集仪是一种常用的结构安全监测工具,可以用于评估建筑物、桥梁、隧道或其他结构的结构健康状态和安全性能。这种监测方案较为先进、精确,并且能够监测长期的结构反应,因此…...

卡尔曼滤波
通过 Eigen 矩阵运算实现线性卡尔曼滤波。模拟的是一辆带火箭发动机的汽车,一开始沿着X轴匀速运动,到X轴中间开启火箭发动机匀加速向Y轴起飞。同理可以仿真(x,y,z,yaw,pitch,raw) 6自由度的真实飞行情况 #include <iostream&g…...
不受平台限制,Sketch 网页版震撼登场
Sketch 是一种基于 Mac 的矢量图形编辑器,可用于数字设计。其主要功能包括无损矢量编辑、完美像素精度和数百个插件同步功能,可导出预设和代码。它是目前流行的页面交互协作设计工具。但是 Sketch 最大的缺点是对 Windows/PC 用户不友好。严格来说&#…...

如何使用.pth训练模型
一.使用.pth训练模型的步骤如下: 1.导入必要的库和模型 import torch import torchvision.models as models# 加载预训练模型 model models.resnet50(pretrainedTrue) 2.定义数据集和数据加载器 # 定义数据集和数据加载器 dataset MyDataset() dataloader to…...
C++11线程以及线程同步
C11中提供的线程类std::thread,基于此类创建一个新的线程相对简单,只需要提供线程函数和线程对象即可 一.命名空间 this_thread C11 添加一个关于线程的命名空间std::this_pthread ,此命名空间中提供四个公共的成员函数; 1.1 get_id() 调用命名空间s…...
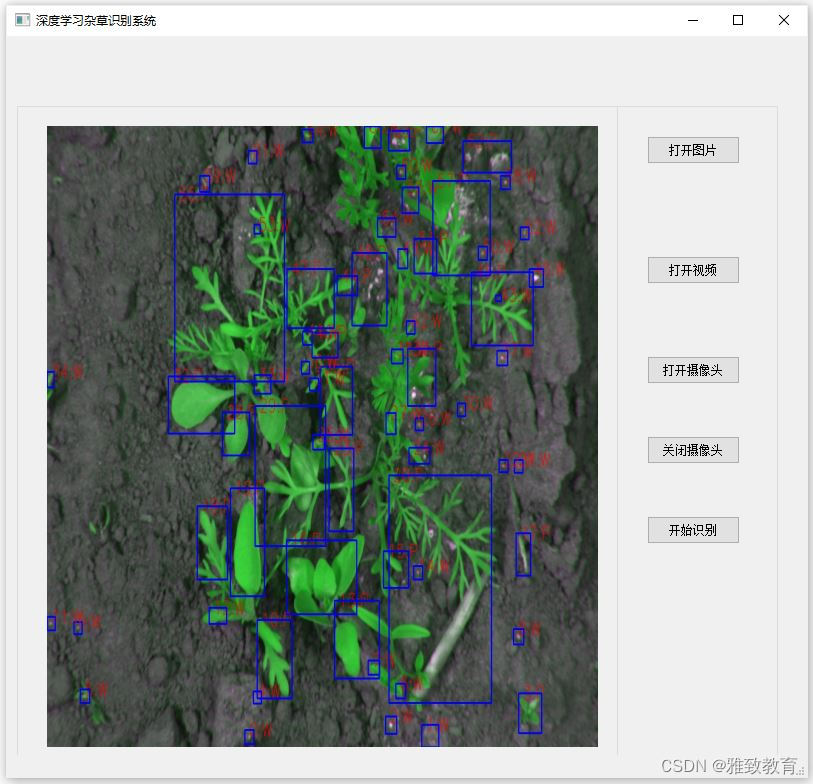
深度学习之基于YoloV3杂草识别系统
欢迎大家点赞、收藏、关注、评论啦 ,由于篇幅有限,只展示了部分核心代码。 文章目录 一项目简介 二、功能三、系统四. 总结 一项目简介 深度学习在图像识别领域已经取得了显著的成果,其中基于YOLO(You Only Look Once)…...

Linux 命令vim(编辑器)
(一)vim编辑器的介绍 vim是文件编辑器,是vi的升级版本,兼容vi的所有指令,同时做了优化和延伸。vim有多种模式,其中常用的模式有命令模式、插入模式、末行模式:。 (二)vim编辑器基本操作 1 进入vim编辑文件 1 vim …...

轻松配置PPPoE连接:路由器设置和步骤详解
在家庭网络环境中,我们经常使用PPPoE(点对点协议过夜)连接来接入宽带互联网。然而,对于一些没有网络专业知识的人来说,配置PPPoE连接可能会有些困难。在本文中,我将详细介绍如何轻松配置PPPoE连接ÿ…...
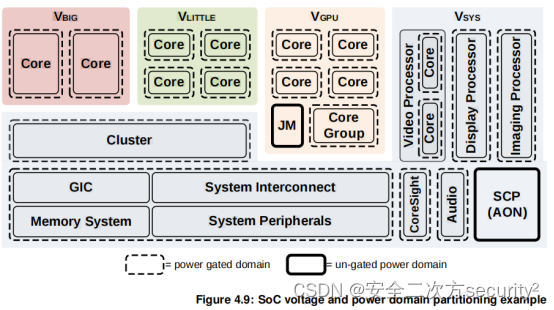
电源控制系统架构(PCSA)之系统分区电源域
目录 4.2 电源域 4.2.1 电源模式 4.2.2 电源域的选择 4.2.3 系统逻辑 4.2.4 Always-On域 4.2.5 处理器Clusters 4.2.6 CoreSight逻辑 4.2.7 图像处理器 4.2.8 显示处理器 4.2.9 其他功能 4.2.10 电源域层次结构要求 4.2.11 SOC域示例 4.2 电源域 电源域在这里被定…...

Linux:docker基础操作(3)
docker的介绍 Linux:Docker的介绍(1)-CSDN博客https://blog.csdn.net/w14768855/article/details/134146721?spm1001.2014.3001.5502 通过yum安装docker Linux:Docker-yum安装(2)-CSDN博客https://blog.…...

【Axure教程】用中继器制作卡片多条件搜索效果
卡片设计通过提供清晰的信息结构、可视化吸引力、易扩展性和强大的交互性,为用户界面设计带来了许多优势,使得用户能够更轻松地浏览、理解和互动。 那今天就教大家如何用中继器制作卡片的模板,以及完成多条件搜索的效果,我们会以…...
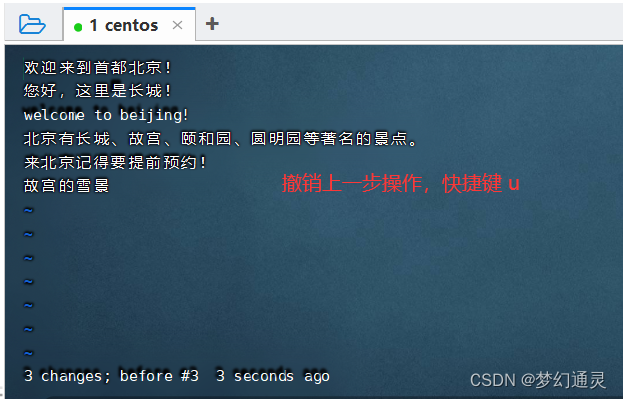
Linux中vi常用命令-批量替换
在日常服务器日志查看中常用到的命令有grep、tail等,有时想查看详细日志,用到vi命令,记录下来,方便查看。 操作文件:test.properites 一、查看与编辑 查看命令:vi 文件名 编辑命令:按键 i&…...

logback-spring.xml的内容格式
目录 一、logback-spring.xml 二、Logback 中的三种日志文件类型 一、logback-spring.xml <?xml version"1.0" encoding"UTF-8"?> <configuration scan"true" scanPeriod"10 seconds" ><!-- <statusListener…...
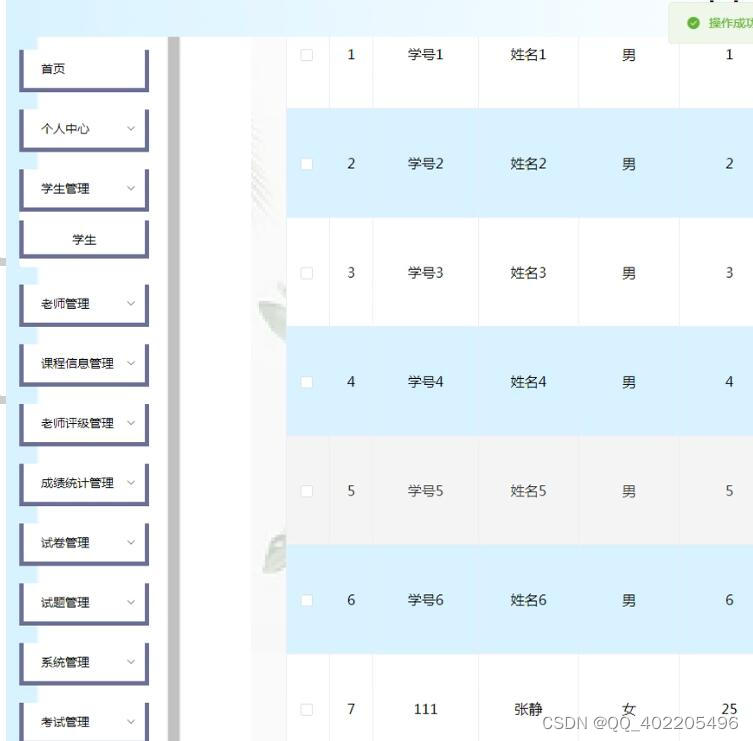
nodejs+vue+elementui+express青少年编程课程在线考试系统
针对传统线下考试存在的老师阅卷工作量较大,统计成绩数据时间长等问题,实现一套高效、灵活、功能强大的管理系统是非常必要的。该系统可以迅速完成随机组卷,及时阅卷、统计考试成绩排名的效果。该考试系统要求:该系统将采用B/S结构…...
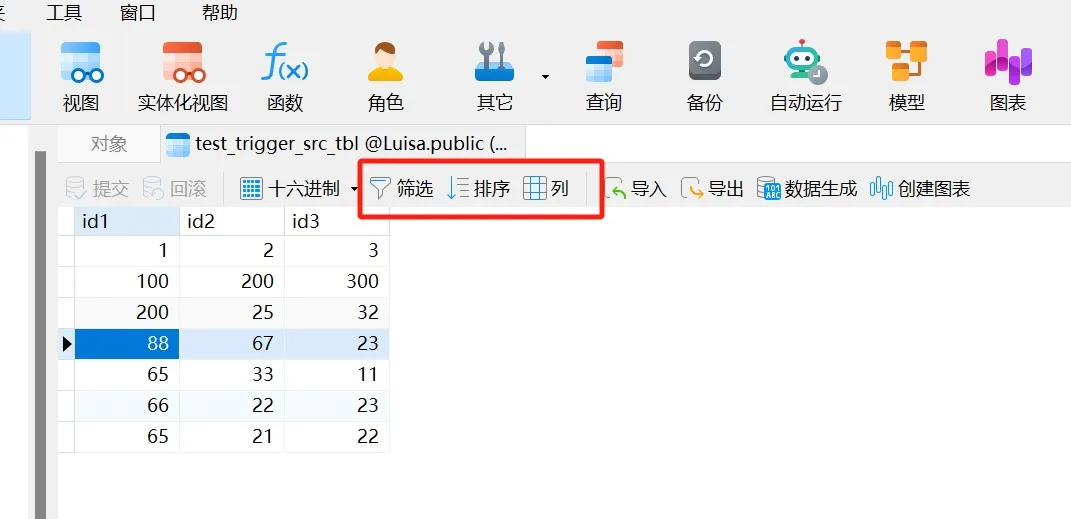
Navicat 技术指引 | GaussDB 数据查看器
Navicat Premium(16.2.8 Windows版或以上) 已支持对GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...

Docker的registry
简介 地址:https://hub.docker.com/_/registry Dcoker registry是存储Dcoker image的仓库,运行push,pull,search时,是通过Dcoker daemon与docker registry通信。有时候会用Dcoker Hub这样的公共仓库可能不方便&#x…...
【vue_3】关于超链接的问题
1、需求2、修改前的代码3、修改之后(1)第一次(2)第二次(3)第三次(4)第四次(5)第五次 1、需求 需求:要给没有超链接的列表添加软超链接 2、修改前…...

redis优化秒杀和消息队列
redis优化秒杀 1. 异步秒杀思路1.1 在redis存入库存和订单信息1.2 具体流程图 2. 实现2.1 总结 3. Redis的消息队列3.1 基于list实现消息队列3.2 基于PubSub实现消息队列3.3 基于stream实现消息队列3.3.1 stream的单消费模式3.3.2 stream的消费者组模式 3.4 基于stream消息队列…...

arm-eabi-gcc 和 arm-none-eabi-gcc 都是基于 GCC 的交叉编译器
arm-eabi-gcc 和 arm-none-eabi-gcc 都是基于 GCC 的交叉编译器,用于编译 ARM 架构的嵌入式系统。它们的命名规则如下: arm 表示目标架构是 ARM。eabi 表示嵌入式应用程序二进制接口(Embedded Application Binary Interface)&…...

《大话设计模式》(持续更新中)
《大话设计模式》 序 为什么要学设计模式第0章 面向对象基础什么是对象?什么是类?什么是构造方法?什么是重载?属性与字段有什么区别?什么是封装?什么是继承?什么是多态?抽象类的目的…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
