【数据结构】二叉树之链式结构

🔥博客主页: 小羊失眠啦.
🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》
❤️感谢大家点赞👍收藏⭐评论✍️

文章目录
- 一、前置说明
- 二、二叉树的遍历
- 2.1 前序遍历
- 2.2 中序遍历
- 2.3 后序遍历
- 2.4 层序遍历
- 三、二叉树的结点个数
- 3.1 二叉树的总结点数
- 3.2 二叉树的叶子结点数
- 3.3 二叉树第k层结点数
- 四、二叉树的高度/深度
- 五、二叉树的查找
- 六、二叉树的创建和销毁
一、前置说明
在学习二叉树各种各样的操作前,我们先来回顾一下二叉树的概念:
二叉树是度不超过2的树,由根结点和左右2个子树组成,每个子树也可以看作一颗二叉树,又可以拆分为根结点和左右两颗子树…
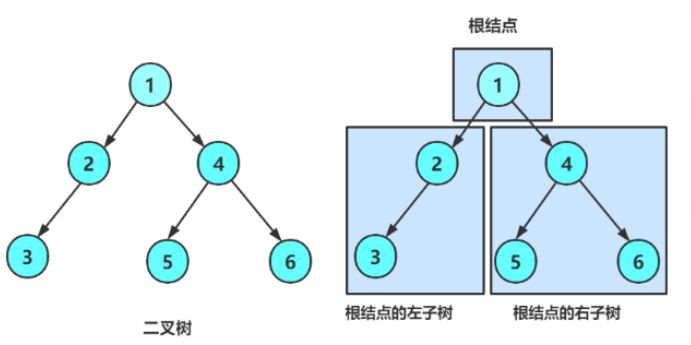
是不是很熟悉,一个大问题可以拆分为两个子问题,每个子问题又可以拆分为更小的子问题,这样层层拆分到不可拆分(遇到空树)的过程,不就是递归吗!因此,我们可以得出:
树是递归定义的,后续树的各种操作正是围绕着这一点进行的。
二、二叉树的遍历
我们先从最简单的操作----遍历学起。所谓二叉树遍历(Traversal)就是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个节点有且只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。二叉树的遍历分为四种:前序遍历、中序遍历、后序遍历和层序遍历。
2.1 前序遍历
前序遍历(Preorder Traversal)又称先根遍历,即先遍历根结点,再遍历左子树,最后遍历右子树。而对于子树的遍历,也服从上述规则。利用递归,我们可以很快地写出代码:
//前序遍历
void PrevOrder(BTNode* root) {//遇到空树,递归终点if (root == NULL) {printf("NULL ");return;}//对根节点进行操作(此处为打印)printf("%d ", root->val);//递归遍历左子树PrevOrder(root->left);//递归遍历右子树PrevOrder(root->right);
}
为了更好地理解这个过程,我们可以画出递归展开图如下:
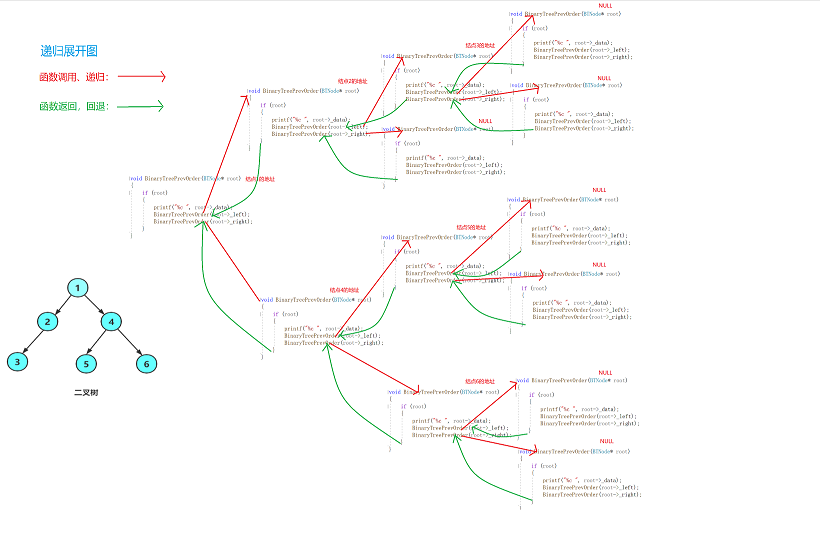
2.2 中序遍历
中序遍历(Inorder Traversal)又称中根遍历,即先遍历左子树,再遍历根结点,最后遍历右子树。同样,子树的遍历规则也是如此。递归代码如下:
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
2.3 后序遍历
后序遍历(Inorder Traversal)又称后根遍历,即先遍历左子树,再遍历右子树,最后遍历根结点。照葫芦画瓢,递归代码如下:
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
2.4 层序遍历
除了上面的前中后序遍历,还可以对二叉树进行层序遍历。所谓层序遍历就是从所在二叉树的根节点出发,首先访问第1层的根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推。这样自上而下,自左向右逐层访问树的结点的过程就是层序遍历。
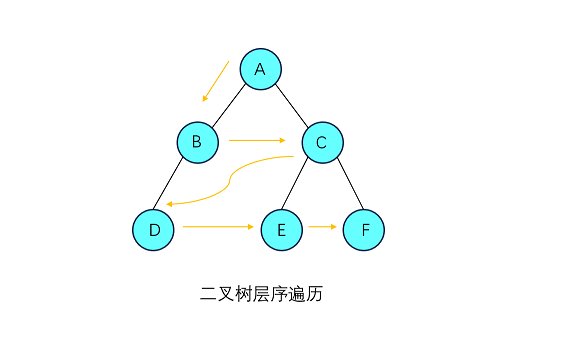
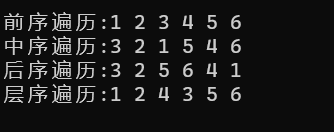
与前面三种遍历不同,层序遍历属于广度优先遍历,因此我们可以利用队列先进先出的特性,将每个结点一层一层依次入队,然后依次出队进行操作即可。具体演示及代码如下:

void LevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ", front->val);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);QueuePop(&q);}printf("\n");QueueDestroy(&q);
}
三、二叉树的结点个数
3.1 二叉树的总结点数
一颗二叉树的结点数我们可以看作是根结点+左子树结点数+右子树结点数,那左右子树的结点数又是多少呢?按照相同的方法继续拆分,层层递归直到左右子树为空树,返回空树的结点数0即可。递归代码如下:
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
3.2 二叉树的叶子结点数
左右子树都为空的结点即是叶子结点。这里分为两种情况:左右子树都为空和左右子树不都为空。
-
当左右子树都为空时,则这颗树的叶子结点数为1(根节点)。
-
当左右子树不都为空,即根结点不是叶子结点时,这棵树的叶子结点数就为
左子树叶子结点数+右子树叶子结点数(空树没有叶子结点)。
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
3.3 二叉树第k层结点数
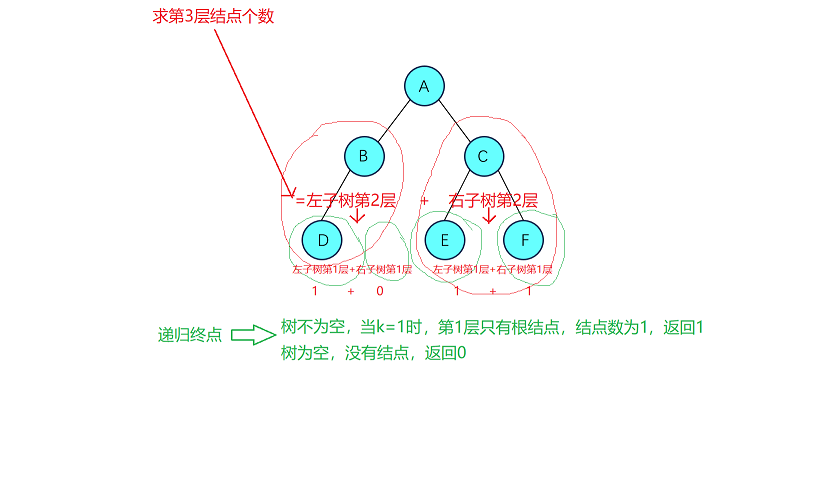
类似的,一颗树第k层的结点数我们可以拆分为其左子树第k-1层结点+右子树第k-1层结点。这样层层递归下去,直到k==1求树的第1层结点数时返回1(树的第1层只有根结点),而如果在递归过程中遇到空树就返回0(空树没有结点)。例如下面一颗树:
int TreeKLevel(BTNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1){return 1;}return TreeKLevel(root->left, k - 1)+ TreeKLevel(root->right, k - 1);
}

四、二叉树的高度/深度
树中结点的最大层次称为二叉树的高度。因此,一颗二叉树的高度我们可以看作是
1(根结点)+左右子树高度的较大值。层层递归下去直到遇到空树返回0即可,递归代码如下:
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}

五、二叉树的查找
二叉树的查找本质上就是一种遍历,只不过是将之前的打印操作换为查找操作而已。我们可以使用前序遍历来进行查找,先比较根结点是否为我们要查找的结点,如果是,之间返回;如果不是,遍历左子树和右子树,返回其查找的结果;如果都找不到,返回空指针。代码如下:
// 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, int x)
{if (root == NULL)return NULL;if (root->val == x)return root;BTNode* ret = NULL;ret = TreeFind(root->left, x);if (ret)return ret;ret = TreeFind(root->right, x);if (ret)return ret;return NULL;
}
六、二叉树的创建和销毁
最后,我们再来看看如何来创建和销毁一颗二叉树。我们前面说过:二叉树是递归定义的。有了前面的基础,二叉树的创建和销毁也就不是什么难事了。
BTNode* BuyNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}// 二叉树销毁
void TreeDestroy(BTNode* root)
{if (root == NULL){return;}TreeDestroy(root->left);TreeDestroy(root->right);free(root);//root = NULL;
}
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位铁汁们的支持。文章有任何问题可以在评论区留言,小羊一定认真修改,写出更好的文章~~

相关文章:

【数据结构】二叉树之链式结构
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 文章目录 一、前置说明二、二叉树的遍历2.1 前序遍历2.2 中序遍历2.3 后序遍历2.4 层序遍历 三、…...

完美的输出打印 SQL 及执行时长[MyBatis-Plus系列]
导读 Hi,大家好,我是悟纤。过着爱谁谁的生活,活出不设限的人生。 在我们日常开发工作当中,避免不了查看当前程序所执行的SQL语句,以及了解它的执行时间,方便分析是否出现了慢SQL问题。 MyBatis-Plus提供了两种SQL分析打印的方式,用于输出每条SQL语句及其执行时间,针…...
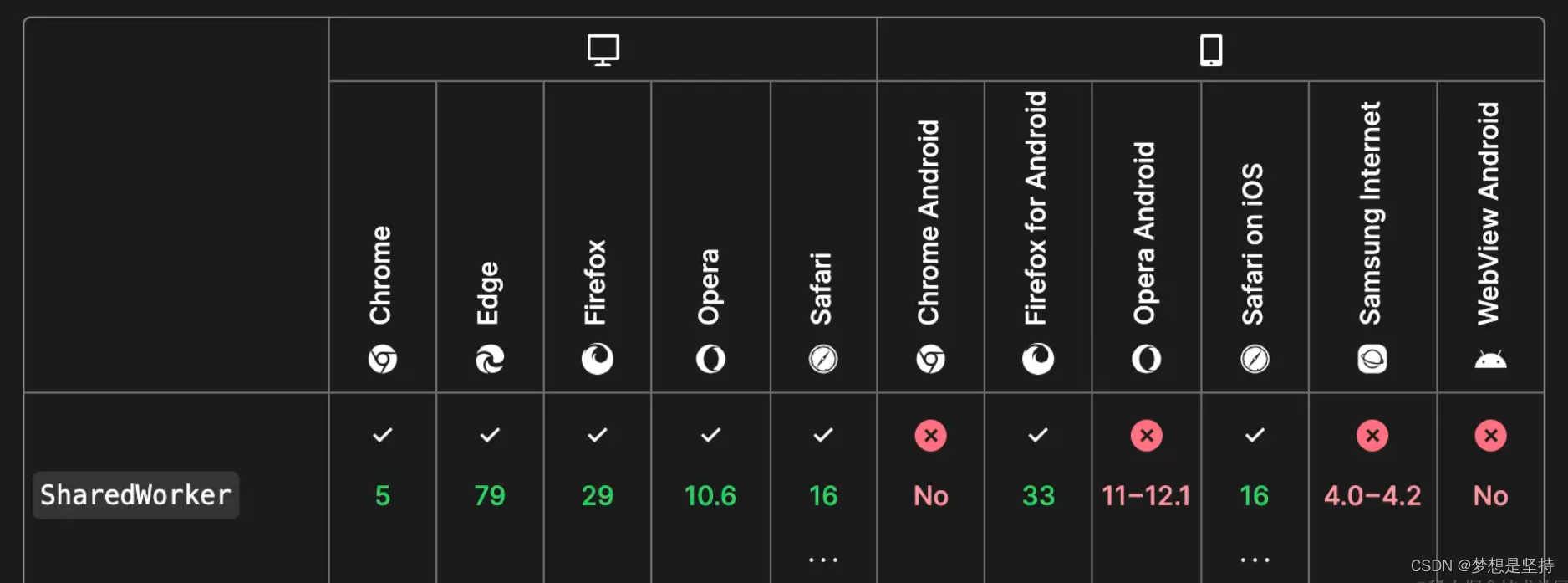
跨标签页通信的8种方式(下)
跨标签页通信是指在浏览器中的不同标签页之间进行数据传递和通信的过程。在传统的Web开发中,每个标签页都是相互独立的,无法直接共享数据。然而,有时候我们需要在不同的标签页之间进行数据共享或者实现一些协同操作,这就需要使用跨…...

笔记二十、使用路由Params进行传递参数
20.1、在父组件中设置路由参数 <NavLink to{classify/${this.state.name}} className{this.activeStyle}>classify</NavLink> 父组件 Home/index.jsx import React from "react"; import {NavLink, Outlet} from "react-router-dom";class Ap…...

K8S----taint、tolerations、label
一、污点(taint),针对的是节点,只有node才有污点的概念 1、 给节点增加一个污点 kubectl taint nodes node1 key1=value1:NoSchedule给节点 node1 增加一个污点,它的键名是 key1,键值是 value1,效果是 NoSchedule。 这表示只有拥有和这个污点相匹配的容忍度的 Pod 才能…...
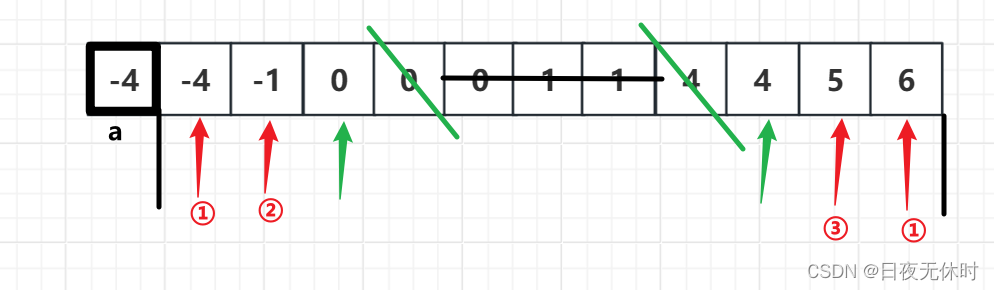
【双指针】三数之和
三数之和 在做这道题之前,建议建议先将两数之和做完再做,提升更大~ 文章目录 三数之和题目描述算法原理解法一解法二思路如下:处理细节问题: 代码编写Java代码编写C代码编写 15. 三数之和 - 力扣(LeetCode࿰…...

CH01_适应设计模式
Iterator模式(迭代器模式) 迭代器模式(Iterator),提供一种方法,顺序访问一个聚合对象中各个元素,而不是暴露该对象的内部表示。 类图结构 说明 Iterator(迭代器) 该角色负责定义按…...
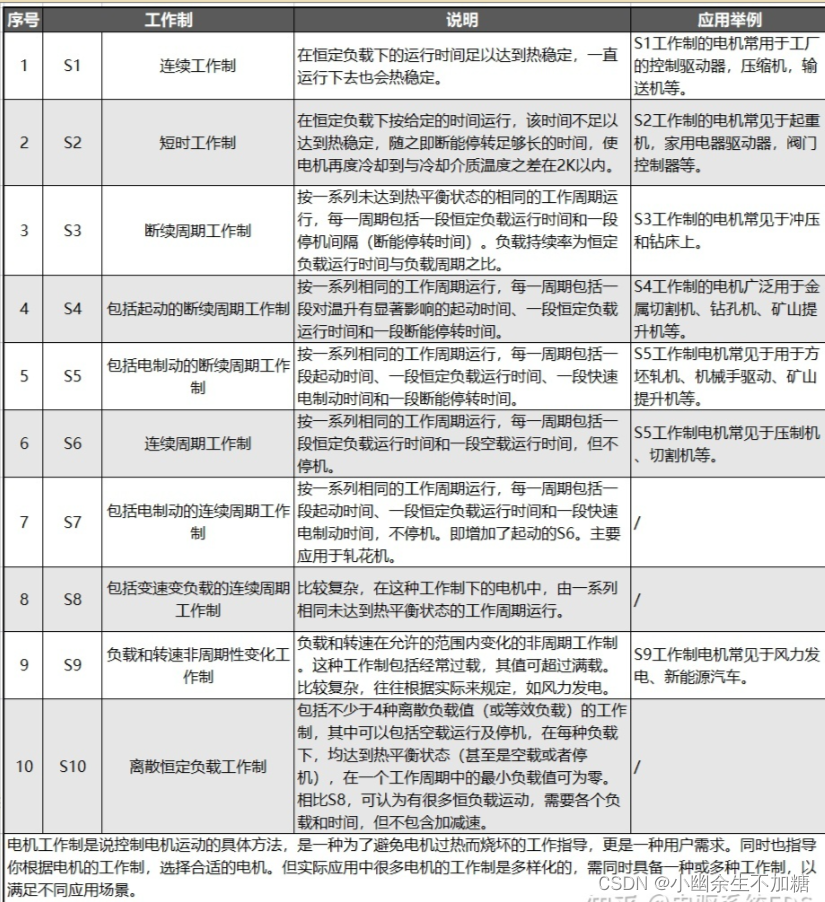
电机工作制
电机工作制 1.什么是电机工作制2.电机工作制的分类 最近在做电机控制器,看到很多电机铭牌上写着工作制:S*,有S1,有S2,查了一下,学习一下是什么意思。 1.什么是电机工作制 根据GBT 755-2019《旋转电机定额…...
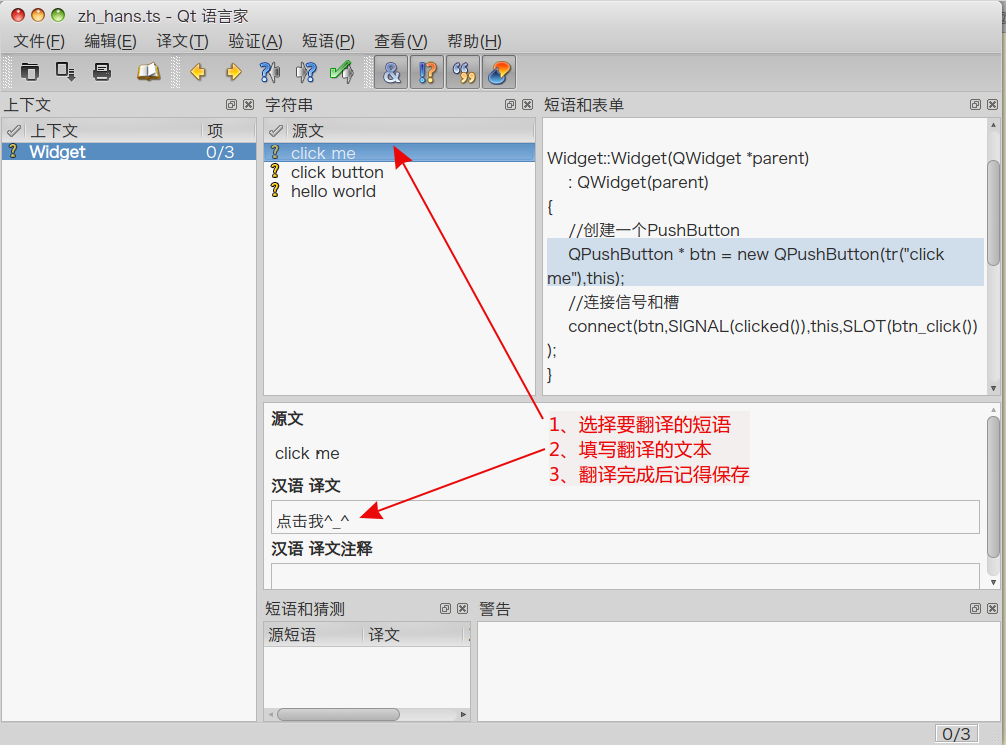
qt国际化多语言
vs + qt 方法 一 (1)生成.pro文件 如果报错: cannot find any qt projects to export 则执行如下: 然后重新生成 pro文件。 (2)生成ts文件 (方法1)在项目文件(xxx.pro) 文件添加: TRANSLATIONS += en.ts zh_CN.ts 然后打开cmd命令,进入项目目录,执行 l…...

Java Excel Poi 单元格内置的数据格式
位置 //在类 org.apache.poi.ss.usermodel.BuiltinFormats 中的私有成员变量_formats中 private static final String[] _formats new String[]{"General", "0", "0.00", "#,##0", "#,##0.00", "\"$\"#,##…...
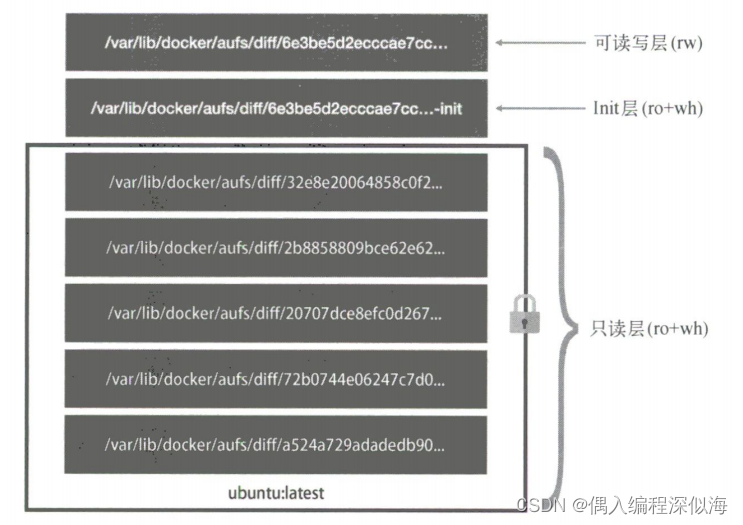
【深入剖析K8s】容器技术基础(三):深入理解容器镜像 文件角度
容器里的进程‘看到’’的文件系统 可能你立刻就能想到,这应该是一个关于MountNamespace的问题:容器里的应用进程理应‘看到”一套完全独立的文件系统这样它就可以在自己的容器目录(比如 /tmp)下进行操作’而完全不会受宿主机以及其他容器的影响。 容器…...
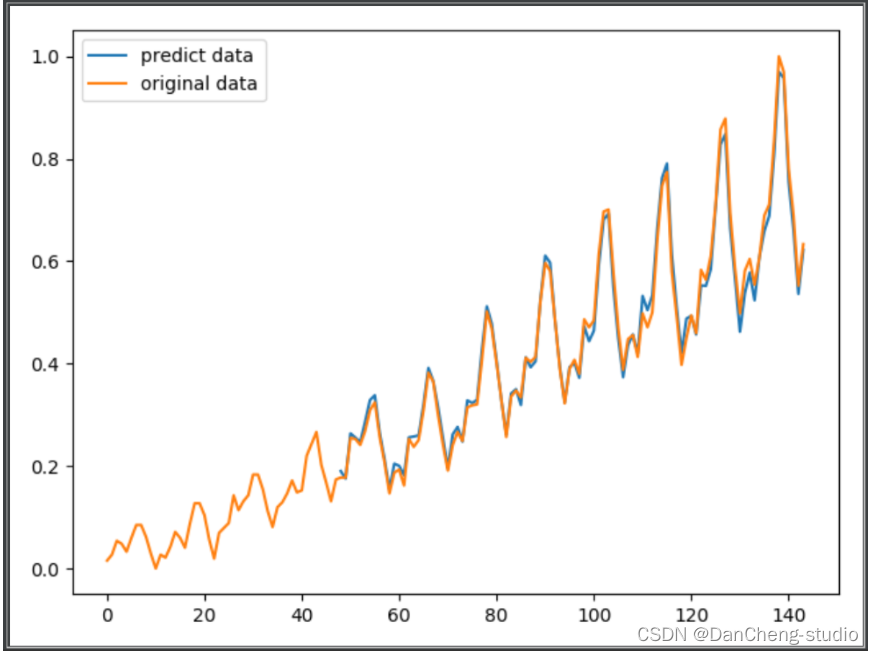
竞赛选题 题目:基于LSTM的预测算法 - 股票预测 天气预测 房价预测
文章目录 0 简介1 基于 Keras 用 LSTM 网络做时间序列预测2 长短记忆网络3 LSTM 网络结构和原理3.1 LSTM核心思想3.2 遗忘门3.3 输入门3.4 输出门 4 基于LSTM的天气预测4.1 数据集4.2 预测示例 5 基于LSTM的股票价格预测5.1 数据集5.2 实现代码 6 lstm 预测航空旅客数目数据集预…...

开源WIFI继电器之源代码
源代码:WiFiRelay: 基于ESP8285的WiFi继电器代码 1、环境搭建 开发环境搭建请参照win10搭建ESP8266_RTOS_SDK编译环境_xtensa-lx106 下载-CSDN博客 2、下载代码 在sdk路径下创建一个projects的文件夹,将WiFiRelay的代码克隆到此目录下: mkdir projec…...

NX二次开发UF_CURVE_create_arc_point_point_radius 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_create_arc_point_point_radius Defined in: uf_curve.h int UF_CURVE_create_arc_point_point_radius(tag_t point1, tag_t point2, double radius, UF_CURVE_limit_p_t l…...

Unsupervised MVS论文笔记(2019年)
Unsupervised MVS论文笔记(2019年) 摘要1 引言2 相关工作3 实现方法3.1 网络架构3.2 通过光度一致性学习3.3 MVS的鲁棒光度一致性3.4 学习设置和实施的细节3.5.预测每幅图像的深度图 4 实验4.1 在DTU上的结果4.2 消融实验4.3 在ETH3D数据集上的微调4.4 在…...

2-Python与设计模式--前言
0-Python与设计模式–前言 一 什么是设计模式 设计模式是面对各种问题进行提炼和抽象而形成的解决方案。这些设计方案是前人不断试验, 考虑了封装性、复用性、效率、可修改、可移植等各种因素的高度总结。它不限于一种特定的语言, 它是一种解决问题的思…...

如何判别使用的junit是4还是5
Junit4与Junit5的版本中,Test注解的包位置不同。 Junit4的Test注解是在org.junit包下,儿Junit5的Test注解是在org.junit.jupiter.api包下。 可据此判定是使用的Junit4还是Junit5。 Junit4 import org.junit.Test;Junit5 import org.junit.jupiter.api…...
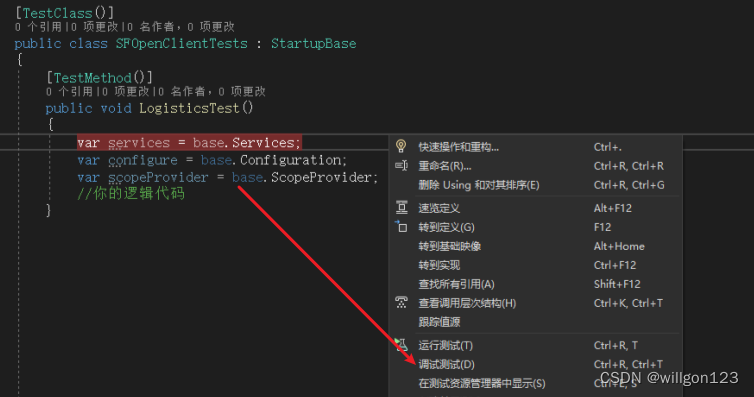
C#-创建用于测试的父类StartupBase用于服务注入
当写完C#代码,需要对某个方法进行测试。 创建一个XXXTests.cs文件之后,发现需要注入某个服务怎么办? 再创建一个StartupBase.cs文件: public abstract class StartupBase {public IConfiguration Configuration { get; }public …...
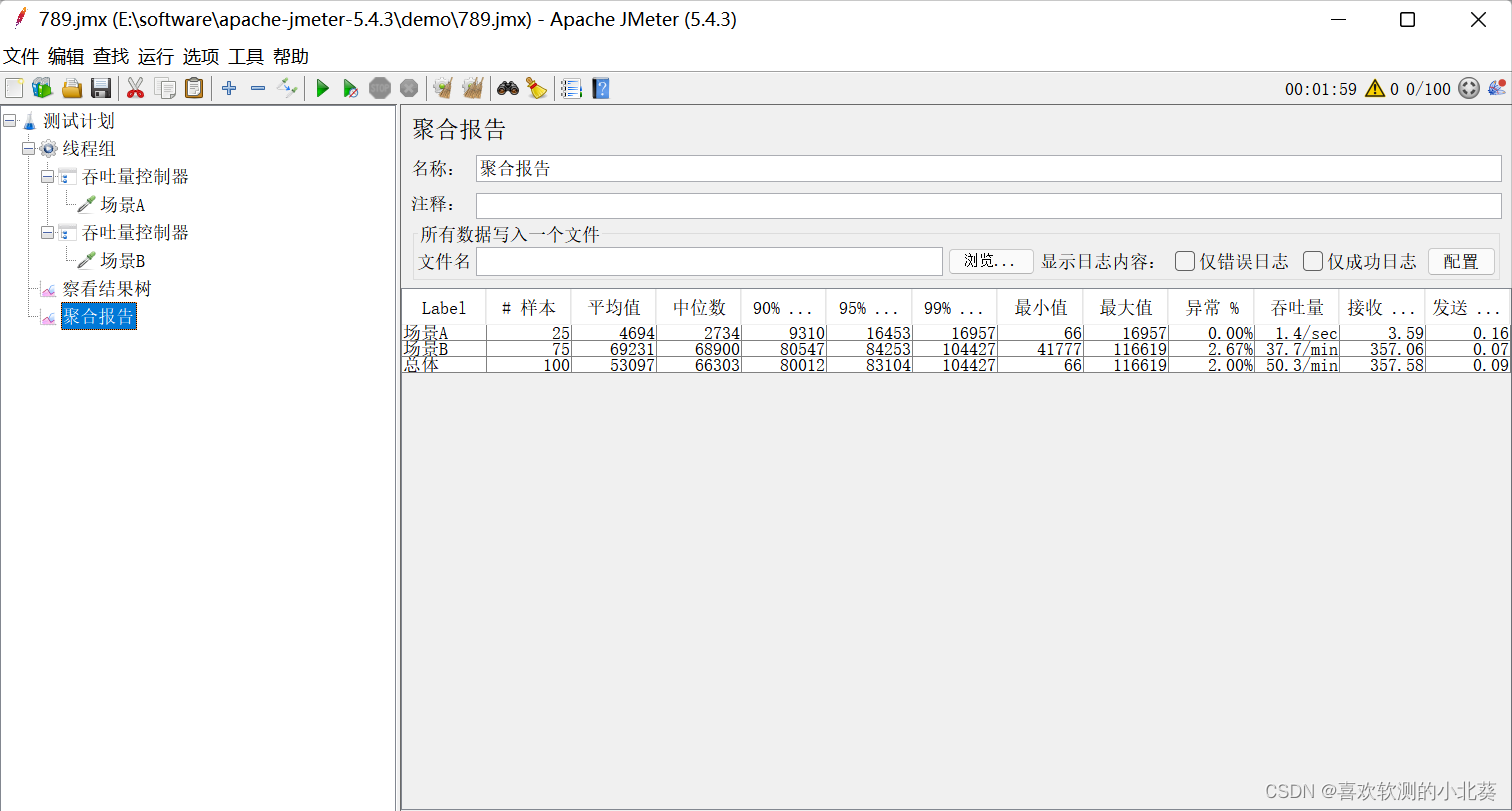
JMeter之压力测试——混合场景并发
在实际的压力测试场景中,有时会遇到多个场景混合并发的情况,这时就需要设置不同的并发比例对不同场景请求数量的控制,下面提供两种方案。 一、多线程组方案 1.业务场景设计如下:场景A、场景B、场景C,三个场景按照并发…...

Python入门04字符串
目录 1 字符串的定义2 转义字符3 字符串的常见方法4 分割字符串5 字符串反转6 字符串的链式调用7 格式化字符串8 多行字符串总结 1 字符串的定义 在Python中,字符串表示一个字符的序列,比如 str "hello,world"这里我们定义了一个字符串&…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
