蓝桥杯-动态规划-子数组问题

目录

一、乘积最大数组

二、乘积为正数的最长子数组长度

三、等差数列划分

四、最长湍流子数组

---

心得：

最重要的还是状态表示，我们需要根据题的意思，来分析出不同的题，不同的情况，来分析需要多少个状态

一、乘积最大数组

乘积最大数组

1.状态表示

dp[i]:到达i位置的最大乘积子数组。

2.状态转移方程

dp[i]=Math.max(dp[i-1]*p[i],dp[i-1]);

问题：不能通过简单的最大值来填表，因为他的这个存在负负得正的情况，但是他其实一共乘法分为两种情况

正*正为正 最大值

正*负为负 最小值

负*负为正 最大值

状态表示更改为

f[i]:到达i位置，最大的乘积

g[i]:到达i位置，最小的乘积

所以状态转移方程也需要去变

 f[i]=Math.max(nums[i],Math.max(f[i-1]*nums[i],g[i-1]*nums[i]));
 g[i]=Math.min(nums[i],Math.min(f[i-1]*nums[i],g[i-1]*nums[i]));

3.初始化

f[0]=g[0]=nums[0]

4.填表顺序

从左到右

5.返回值

class Solution {public int maxProduct(int[] nums) {int m=nums.length;//f为最大乘积和//g为最小乘积和int[]f=new int[m];int[]g=new int[m];f[0]=g[0]=nums[0];for(int i=1;i<m;i++){//f[i]状态表示f[i]=Math.max(nums[i],Math.max(f[i-1]*nums[i],g[i-1]*nums[i]));g[i]=Math.min(nums[i],Math.min(f[i-1]*nums[i],g[i-1]*nums[i]));}
int ret =-0x3f3f3f3f;for(int i=0;i<m;i++){ret=Math.max(ret,f[i]);}return  ret;}
}

二、乘积为正数的最长子数组长度

1.状态表示

dp[i]=到达i位置乘积为正数的最长子数组长度

如果要确保乘积是正数，就需要我们上面那个乘积最大的数组的状态表示

f[i]:以i元素为结尾位置，乘积为正数的长度

g[i]:以i位置为结尾位置，乘积为负数的长度

2.状态转移方程

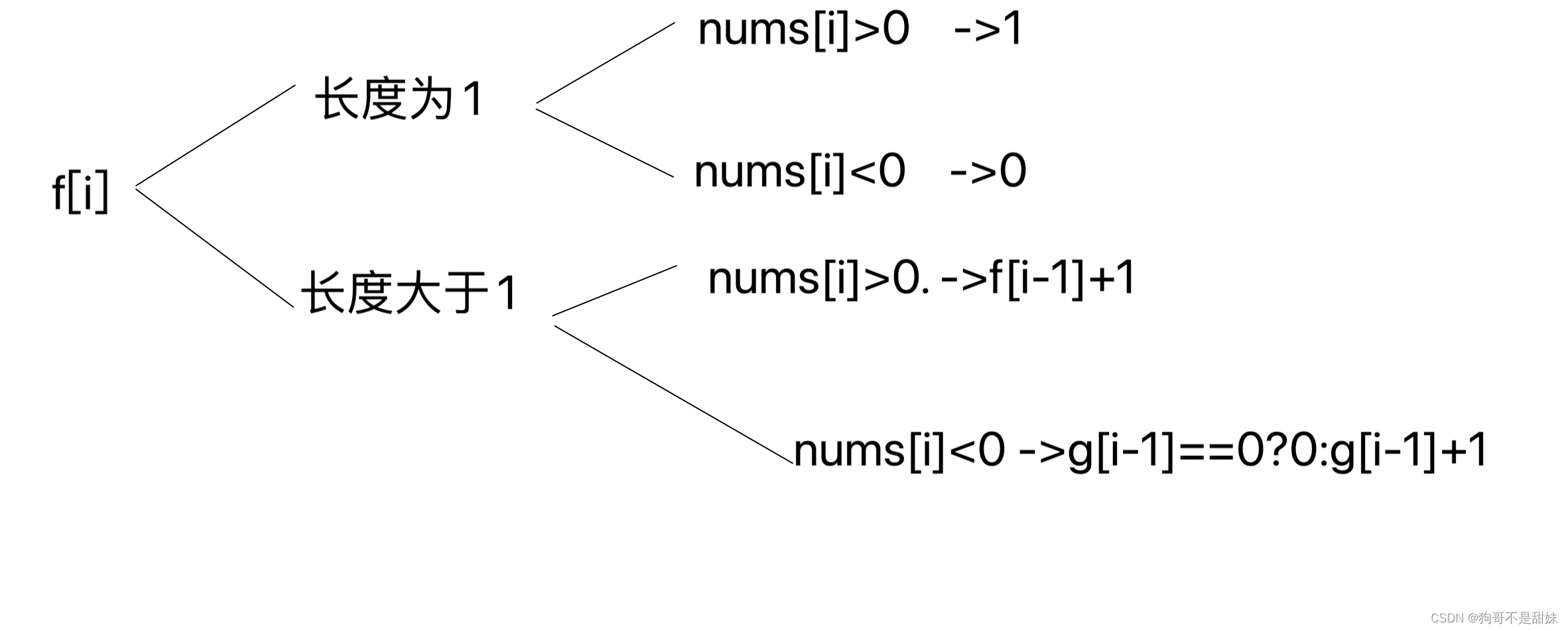
f[i]分为长度为1的情况和长度不为1的情况

长度为一的情况，还要区分是不是为正数

长度不为一的情况，看当前i是正数还是负数

当nums[i]<0的时候我们要想一件事情，假如说g[i-1]正好等于0，然而此时nums[i]<0，那么没有正数,最后的结果不就是等于0吗。所以我们不能写作当nums[i]<0时候，f[i]=g[i-1]+1

3.初始化：

就单纯的看nums[0]大于0还是小于0。 大于0那么f[0]就是1。小于0那么g[0]是1

4.填表顺序：

从左到右

5返回值：返回值最大值

class Solution {public static int getMaxLen(int[] nums) {int m=nums.length;int f[]=new int[m];int g[]=new int[m];if(nums[0]>0){f[0]=1;}else if(nums[0]<0){g[0]=1;}for(int i=1;i<m;i++){//f[i]状态表示if(nums[i]>0){f[i]=f[i-1]+1;if(g[i-1]==0){g[i]=0;}else{g[i]=g[i-1]+1;}}else if(nums[i]<0){if(g[i-1]==0){f[i]=0 ;}else{f[i]=g[i-1]+1;}g[i]=f[i-1]+1;}}int ret=0;for(int i=0;i<m;i++){ret=Math.max(ret,f[i]);}return ret;}}

三、等差数列划分

1.状态表示

dp[i]到达i位置等差数列的个数

2.状态表示

如果nums[i]-nums[i-1]==nums[i-1]-nums[i-2]，那么他就构成了一个三个数的等差数组,

如果他之前就是三个数的等差数组，加一个数也就可以组成一个四个数的等差数组

dp[i]=dp[i-1]+1 (多少个数的等差数组）然后假如说由3个变成4个，4-3也就是要加1即可，剩下的那个是在三个里面，换句话说，有上面那个判定条件，它是给你判定三个的，但是假如说你这个是4个，他就不会算在内，所以4个的话就要多加1，五个就要多加一个4个，和一个五个，这样慢慢的规律就是i-2即可（我的意思是假如是五个减去三个）

然后检查三个的是不是一个等差数组

3.初始化:

小于3就是0

4.填表顺序:

从左到右

5.返回值

return dp表中的最大值即可

class Solution {public static int numberOfArithmeticSlices(int[] nums) {int m=nums.length;int[]dp=new int[m];if(m<3){return 0;}int max=0;for(int i=2;i<m;i++){if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){dp[i]=dp[i-1]+1;if(i-2>0&&dp[i-1]!=0){dp[i]=dp[i]+i-2;}max=Math.max(dp[i-1],max);if(i-2>0&&dp[i-1]==0){dp[i]=max+1;}max=Math.max(dp[i],max);}}int ret=0;for(int i=0;i<m;i++){ret=Math.max(dp[i],ret);}return ret;}
}

四、最长湍流子数组

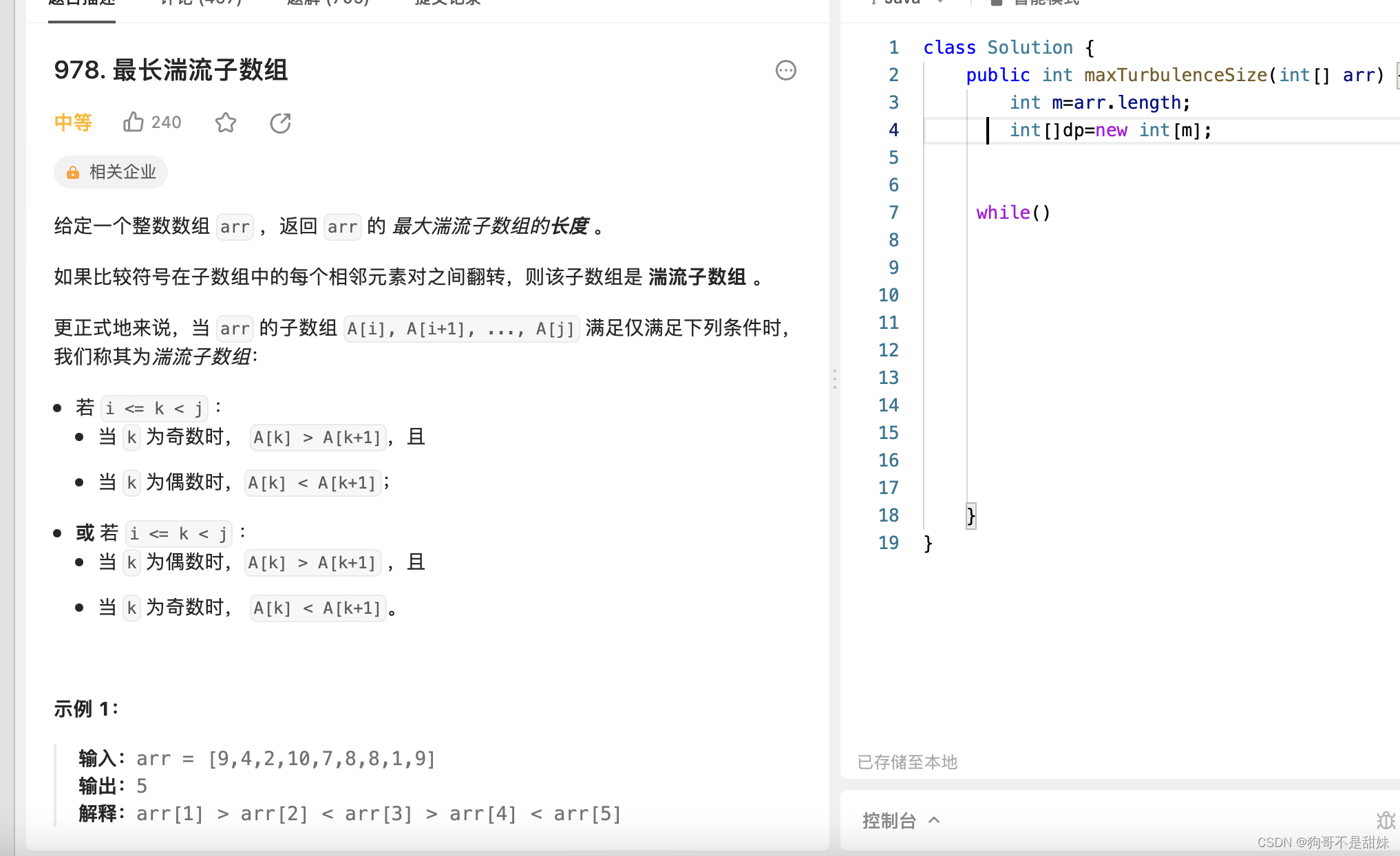
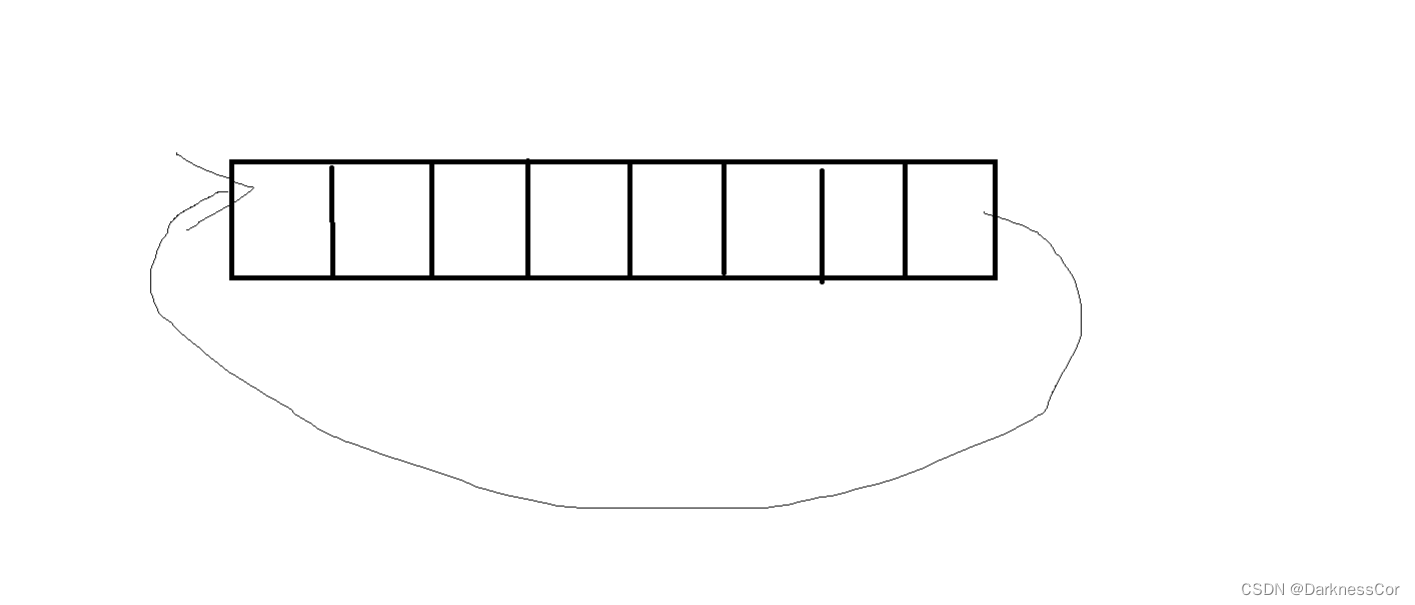
湍流数组用图来表示就相当于是

大概就是这种图像的含义。*        *
*       *

1.状态表示

dp[i]:到达i位置的最长湍流数组的长度

2.状态表示

if(n%2==0){

假如nums[i]>nums[i+1]}

else{

nums[i]<nums[i+1]}

dp[i]=dp[i-1]+1

在这里我们发现一件事情，一个数组，他最多只能表示当前的一种情况

但这个地方有三个状态，所以不能说单靠一个表达湍流数组的状态

所以我们决定使用f[i],g[i],来表示，前面两种情况，最后那个是0

f[i]:表示在i位置，与i-1位置呈现下降趋势,最长湍流数组长

g[i]:表示在i位置，与i-1位置呈现上升趋势，最长湍流数组长

那么if(nums[i-1]>nums[i]){

f[i]=g[i-1]+1;

g[i]=1;

}

if(nums[i]<nums[i+1]){

f[i]=1；

g[i]=f[i-1]+1;

}

3.初始化

因为假如只有一个数字，那么湍流数组的长度是1，所以说，这个就默认是1了。

从1到n

4.填表顺序

从左到右

5.返回值

返回最大值

class Solution {public int maxTurbulenceSize(int[] arr) {int m=arr.length;int[]f=new int[m];int[]g=new int[m];for(int i=0;i<m;i++){f[i]=g[i]=1;}for(int i=1;i<m;i++){if(arr[i-1]>arr[i]){f[i]=g[i-1]+1;g[i]=1;}if(arr[i-1]<arr[i]){f[i]=1;g[i]=f[i-1]+1;}}int ret=0;for(int i=0;i<m;i++){ret=Math.max(ret,Math.max(g[i],f[i]));}return ret;}
}