C++二分查找:统计点对的数目
本题其它解法
C++双指针算法:统计点对的数目
本周推荐阅读
C++二分算法:得到子序列的最少操作次数
本文涉及的基础知识点
二分查找算法合集
题目
给你一个无向图,无向图由整数 n ,表示图中节点的数目,和 edges 组成,其中 edges[i] = [ui, vi] 表示 ui 和 vi 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。
第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目:
a < b
cnt 是与 a 或者 b 相连的边的数目,且 cnt 严格大于 queries[j] 。
请你返回一个数组 answers ,其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。
请注意,图中可能会有 多重边 。
示例 1:
输入:n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出:[6,5]

解释:每个点对中,与至少一个点相连的边的数目如上图所示。
answers[0] = 6。所有的点对(a, b)中边数和都大于2,故有6个;
answers[1] = 5。所有的点对(a, b)中除了(3,4)边数等于3,其它点对边数和都大于3,故有5个。
示例 2:
输入:n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出:[10,10,9,8,6]
参数范围:
2 <= n <= 2 * 104
1 <= edges.length <= 105
1 <= ui, vi <= n
ui != vi
1 <= queries.length <= 20
0 <= queries[j] < edges.length
分析
时间复杂度
每个查询的时间复杂度是O(nlogn+m)。m的边数。
步骤
每个查询分两步:
一,和a或b相连的边数,严格大于iQue的点对数量。注意,同时和a和b相连算两次,只和a或b相连算一次。
二,枚举各边。如果符合第一步,扣除本边数量后,不再符合题意则减掉。本解法在预处理阶段确保v[0]大于v[1]。
注意:本解题将a和b都减一,这样其范围为:[0,n)。
变量解释
| m_vNodeToCount | m_vNodeToCount[i]=x,有x条边和i相连 |
| m_vCounts | m_vNodeToCount的升序,第一步只考虑和a或b相连的边数,不需要知道a和b的具体值 |
| m_mMaskCount | 各边数量,key是a和b的编码,value是数量 |
代码
核心代码
class Solution {
public:vector<int> countPairs(int n, vector<vector<int>>& edges, vector<int>& queries) { m_iN = n;m_vNodeToCount.resize(n);for (auto& v : edges){if (v[0] < v[1]){swap(v[0], v[1]);}v[0]--;v[1]--; m_vNodeToCount[v[0]]++;m_vNodeToCount[v[1]]++;m_mMaskCount[Mask(v[0], v[1])]++;}m_vCounts = m_vNodeToCount;sort(m_vCounts.begin(), m_vCounts.end());vector<int> vRet;for (const auto& que : queries){vRet.emplace_back(Query(que));}return vRet;}int Query(int iQue)const{int iNum = 0;// 包括a或b的边数大于iQue的数量,(a,b)和(b,a)会重复结算for (auto left = m_iN - 1; left >= 0 ; left--){ iNum += m_vCounts.end() - std::upper_bound(m_vCounts.begin()+left+1, m_vCounts.end(),iQue-m_vCounts[left]);}//扣处重复数量for (const auto& [iMask, iNum1] : m_mMaskCount){auto [a, b] = Parse(iMask);const int tmp = m_vNodeToCount[a] + m_vNodeToCount[b] - iQue;if (tmp > 0 ){if (tmp <= iNum1){iNum--;}}} return iNum;}int Mask(int a, int b){return a * m_iUnit + b;}std::pair<int,int> Parse(const int iMask)const{return std::make_pair(iMask / m_iUnit, iMask % m_iUnit);}const int m_iUnit = 1000 * 100;unordered_map<int, int> m_mMaskCount;vector<int> m_vNodeToCount;vector<int> m_vCounts;int m_iN;
};
测试用例
template <class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template <class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}
}int main()
{int n;vector<vector<int>> edges;vector<int> queries;vector<int> res;{ n = 4;edges = { {1,2},{2,4},{1,3},{2,3},{2,1} };queries = { 2,3 };Solution slu;res = slu.countPairs(n, edges, queries);Assert(res, vector<int>{6, 5});}{n = 5;edges = { {1,5},{1,5},{3,4},{2,5},{1,3},{5,1},{2,3},{2,5} };queries = { 1,2,3,4,5 };Solution slu;res = slu.countPairs(n, edges, queries);Assert(res, vector<int>{10, 10, 9, 8, 6});}//CConsole::Out(res);
}
2023年3月版代码
class Solution {
public:
vector countPairs(int n, vector<vector>& edges, vector& queries) {
m_vDeg.resize(n + 1);
m_iN = n;
for (const auto& v : edges)
{
m_vDeg[v[0]]++;
m_vDeg[v[1]]++;
m_mEdgeNums[min(v[0], v[1])m_llMul + max(v[0], v[1])]++;
}
vector vRet;
for (const auto& q : queries)
{
vRet.push_back(Query1(q) - Query2(q));
}
return vRet;
}
long long Query1(int iQuery)
{
CTreeArr tree(1000100 + 1);
long long iRet = 0;
for (int i = 1; i <= m_iN; i++)
{
const int iMin = iQuery - m_vDeg[i];
const int iLessEqualNum = (iMin>=0) ? tree.Sum(iMin ) : 0;
iRet += (i - 1) - iLessEqualNum;
tree.Add(m_vDeg[i],1);
}
return iRet;
}
long long Query2(int iQuery)
{
long long llSub = 0;
for (auto it : m_mEdgeNums)
{
const int iNum1 = m_vDeg[it.first%m_llMul] + m_vDeg[it.first/m_llMul];
if (iNum1 <= iQuery)
{
continue;
}
if (iNum1 - it.second <= iQuery)
{
llSub++;
}
}
return llSub;
}
long long m_llMul = 1000 * 100;
vector m_vDeg;
std::unordered_map<long long, int> m_mEdgeNums;
int m_iN;
};
2023年7月版代码
class Solution {
public:
vector countPairs(int n, vector<vector>& edges, vector& queries) {
m_vConnectNums.resize(n + 1);
m_n = n;
for (const auto& v : edges)
{
m_vConnectNums[v[0]]++;
m_vConnectNums[v[1]]++;
m_mEdgeMaskNum[ToMask(v)]++;
}
m_iMaxSize = *std::max_element(m_vConnectNums.begin(), m_vConnectNums.end());
vector vRet;
for (const auto& que : queries)
{
vRet.emplace_back(Query(que));
}
return vRet;
}
int Query(const int iQuery)
{
CTreeArr treeArr(m_iMaxSize + 1);
int iRet = 0;
for (int i = 1; i <= m_n; i++)
{
const int iCurSize = m_vConnectNums[i];
int iMin = iQuery - iCurSize;
if (iMin < 0)
{
iRet += (i - 1);
}
else if (iMin >= m_iMaxSize)
{
}
else
{
const int iSum1 = treeArr.Sum(m_iMaxSize);
const int iSum2 = treeArr.Sum(iMin);
iRet += iSum1 - iSum2;
}
treeArr.Add(iCurSize, 1);
}
for (const auto& it : m_mEdgeMaskNum)
{
const int iNum = m_vConnectNums[it.first / 100000] + m_vConnectNums[it.first % 100000];
if (iNum <= iQuery)
{
continue;
}
if (iNum - it.second <= iQuery)
{
iRet–;
}
}
return iRet;
}
int ToMask(const vector& v)
{
return min(v[0], v[1]) * 100000 + max(v[0], v[1]);
}
std::unordered_map<int, int> m_mEdgeMaskNum;
vector m_vConnectNums;
int m_n;
int m_iMaxSize;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
相关文章:

C++二分查找:统计点对的数目
本题其它解法 C双指针算法:统计点对的数目 本周推荐阅读 C二分算法:得到子序列的最少操作次数 本文涉及的基础知识点 二分查找算法合集 题目 给你一个无向图,无向图由整数 n ,表示图中节点的数目,和 edges 组成…...
:了解FFmpeg与SDL常用对象和函数)
播放器开发(二):了解FFmpeg与SDL常用对象和函数
学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 前言 这一篇内容就是简单的了解一遍一些常用的函数名称和作用,混个眼熟。 能看源码的就去看源码!!! 能看源码的就去看源码!!! …...

【数据库】基于排序算法的去重,集合与包的并,差,交,连接操作实现原理,执行代价以及优化
基于两趟排序的其它操作 专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏…...
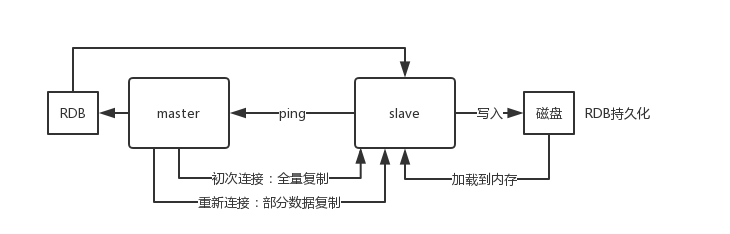
Redis 主从架构,Redis 分区,Redis哈希槽的概念,为什么要做Redis分区
文章目录 Redis 主从架构redis replication 的核心机制redis 主从复制的核心原理过程原理Redis集群的主从复制模型是怎样的?生产环境中的 redis 是怎么部署的?机器是什么配置?你往内存里写的是什么数据?说说Redis哈希槽的概念&…...

极客大挑战2023 Web方向题解wp 全
最后排名 9/2049。 玩脱了,以为28结束,囤的一些flag没交上去。我真该死啊QAQ EzHttp 前言:这次极客平台太安全了谷歌不给抓包,抓包用burp自带浏览器。 密码查看源码->robots.txt->o2takuXX’s_username_and_password.txt获…...
kafka开发环境搭建
文章目录 1 安装java环境1.1 下载linux下的安装包1.2 解压缩安装包1.3 解压后的文件移到/usr/lib目录下1.4 配置java环境变量 2 kafka的安装部署2.1 下载安装kafka2.2 配置和启动zookeeper2.3 启动和停止kafka 1 安装java环境 1.1 下载linux下的安装包 (1…...

Python大数据考题
Python大数据考题: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤其sql要…...

才聚免费为你招聘,用人单位看过来!
才聚团队从1998年开始从事项目管理的推广工作,20多年来培训学员超30万人次,分布全国各地、服务企业超过5000家。拥有大批 PMP (项目管理专业人员资格) NPDP(产品经理国际资格) 软考 (信息系统…...
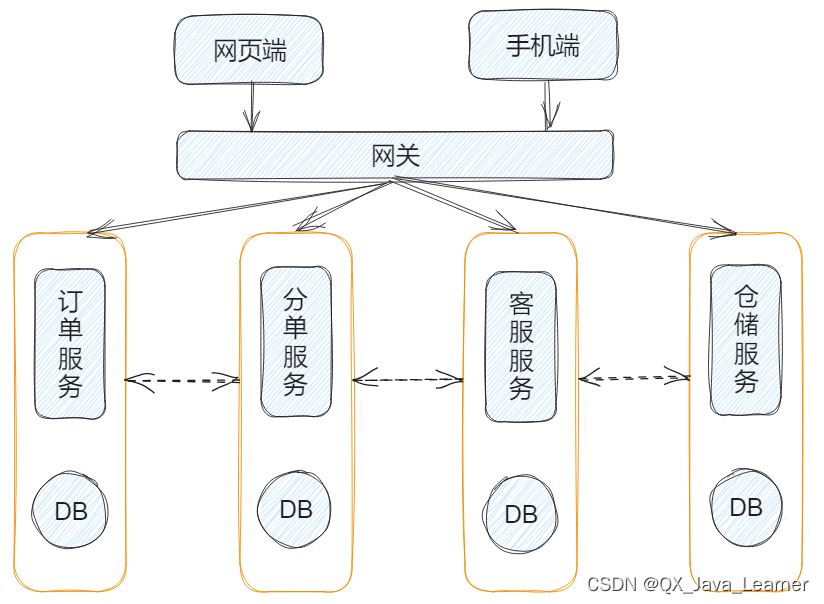
【SpringCloud】微服务的扩展性及其与 SOA 的区别
一、微服务的扩展性 由上一篇文章(没看过的可点击传送阅读)可知, 微服务具有极强的可扩展性,这些扩展性包含以下几个方面: 性能可扩展:性能无法完全实现线性扩展,但要尽量使用具有并发性和异步…...
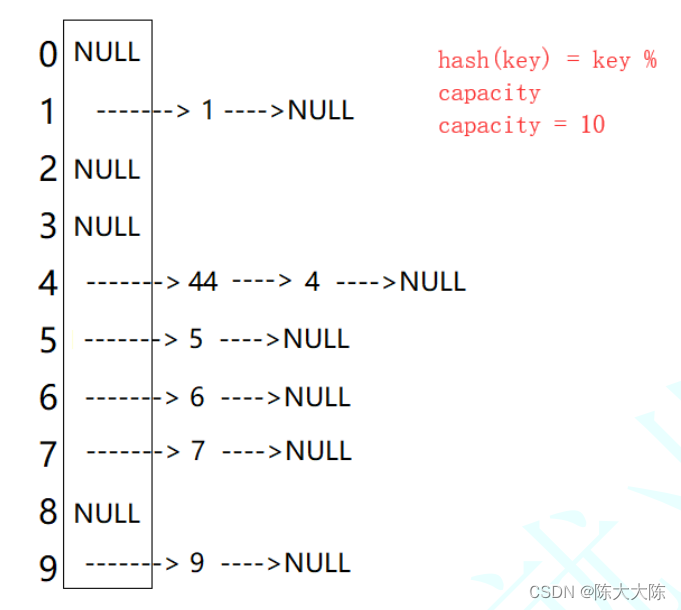
从零带你底层实现unordered_map (2)
💯 博客内容:从零带你实现unordered_map 😀 作 者:陈大大陈 🚀 个人简介:一个正在努力学技术的准C后端工程师,专注基础和实战分享 ,欢迎私信! 💖 欢迎大家…...

打造企业AI数字人专属IP的重要性
在数字化时代,企业数字人专属IP的打造成为了企业品牌建设的重要组成部分。企业数字人专属IP是指是利用人工智能技术实现与真人直播形象的1:1克隆,即克隆出一个数字化的真人形象,作为独有的企业数字人形象,可以用于产品推广、品牌宣…...
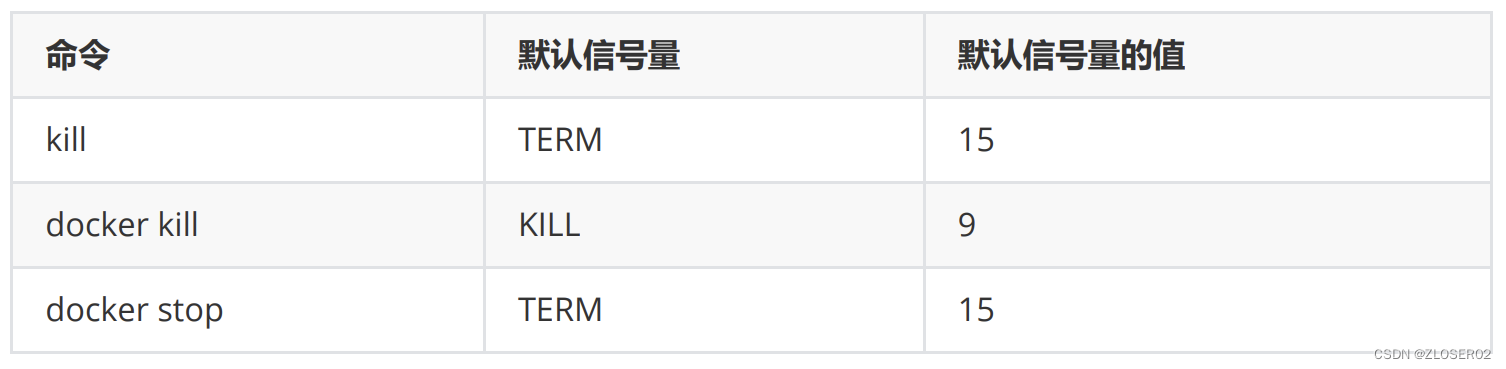
docker容器的生命周期管理常用命令
容器的生命周期管理命令 docker create :创建一个新的容器但不启动它 docker create nginx docker run :创建一个新的容器并运行一个命令 常用选项: 常用选项1. --add-host:容器中hosts文件添加 host:ip 映射记录 2. -a, --attach&#…...

CF 1900B Laura and Operations 学习笔记
原题链接 传送门 题意 输入三个数字a,b,c表示1,2,3的数目,也就是说有a个1,b个2,c个3,每一次可以删除两个不同的数字,增加一个剩下的数字,比如说删除1和3,增加2&#x…...

Linux学习笔记6-串口应用
到现在为止都是在开发板上运行的裸机程序,相当于之前学习STM32单片机时走过的路,还没有真正进入到核心的驱动开发部分,但这都是基础,所以慢慢来不着急。 接下来进入串口通信的学习,和GPIO一样,也是和单片机…...

ubuntu下如何查看.gz压缩包中的内容,以及grep过滤查找文件中的某些内容
1、查看压缩包file.gz中的全部内容 $ zcat file.gz 2、对一个.gz的压缩包解压缩 $ gunzip file.gz 3、过滤查找文件中的某些内容 $ grep "Hello" file.txt 注:我通常先解压,然后再grep 4、过滤查找文件中的内容,并显示其上下3行…...

AI 重构工业制造的故事 我们从大模型开始讲起
在数字化浪潮的推动下,工业制造领域正经历着一场前所未有的变革。人工智能(AI)作为这场变革的关键推动者之一,正以惊人的速度颠覆传统制造业。而大模型作为AI时代最先进的科技工具之一,或将成为引领这场变革的利器&…...
easyExcel 注解开发 快速以及简单上手 以及包含工具类
easyExcel 简单快速使用 1. mevan 这里版本我这里选的是 poi 4.1.2和 ali的easyexcel 的 3.3.1。 因为阿里easy是根据poi的依赖开发的有关系,两者需要对应要不然就会有很多bug和错误在运行时发生。需要版本对应,然而就是easy的代码也会有bug这个版本是比…...
VS2010配置opencv2.4.10
1.下载opencv2.4.10,百度网盘链接如下: 链接:https://pan.baidu.com/s/1UdoQJbRUEB_G2urT703xYQ 提取码:7lbd 2.运行opencv-2.4.10.exe,将文件提取到一个自定义目录里: 3.添加系统环境变量 在“系统变量…...

Android:控制按键灯亮灭【button-backlight】
/frameworks/base/services/core/java/com/android/server/policy/PhoneWindowManager.java 1.导包 import java.io.DataOutputStream; import java.io.FileOutputStream; Handler mHandler3; 2.新建handler对象 public void init(Context context, IWindowManager windowMan…...

1、nmap常用命令
文章目录 1. 主机存活探测2. 常见端口扫描、服务版本探测、服务器版本识别3. 全端口(TCP/UDP)扫描4. 最详细的端口扫描5. 三种TCP扫描方式(1)TCP connect 扫描(2)TCP SYN扫描(3)TCP …...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
