【LeetCode】121. 买卖股票的最佳时机
121. 买卖股票的最佳时机
难度:简单
题目
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 10^50 <= prices[i] <= 10^4
个人题解
方法一:模拟
思路:遍历数组记录当前最小值,且每次比最小值小时都重置最大值,因为大的值只能在最小值的右边找,比较最大最小值的差值,当大于前面记录的最大差值时才替换当前最大差值,这个最大差值即最后要返回的结果
class Solution {public int maxProfit(int[] prices) {int min = Integer.MAX_VALUE;int max = -1;int result = 0;for (int i = 0; i < prices.length; i++) {if (prices[i] < min) {min = prices[i];max = -1;} else if (prices[i] > max) {max = prices[i];result = Math.max(max - min, result);}}return result;}
}
复杂度分析
- 时间复杂度:O(n)
- 空间复杂度:O(1)
官方题解:
我们需要找出给定数组中两个数字之间的最大差值(即,最大利润)。此外,第二个数字(卖出价格)必须大于第一个数字(买入价格)。
形式上,对于每组 i 和 j (其中 i > j)我们需要找出 max(prices[j] - prices[i])
方法一:暴力法【超时】
public class Solution {public int maxProfit(int[] prices) {int maxprofit = 0;for (int i = 0; i < prices.length - 1; i++) {for (int j = i + 1; j < prices.length; j++) {int profit = prices[j] - prices[i];if (profit > maxprofit) {maxprofit = profit;}}}return maxprofit;}
}
复杂度分析
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
方法二:一次遍历
public class Solution {public int maxProfit(int prices[]) {int minprice = Integer.MAX_VALUE;int maxprofit = 0;for (int i = 0; i < prices.length; i++) {if (prices[i] < minprice) {minprice = prices[i];} else if (prices[i] - minprice > maxprofit) {maxprofit = prices[i] - minprice;}}return maxprofit;}
}
复杂度分析
- 时间复杂度:O(n)
- 空间复杂度:O(1)
作者:力扣官方题解
链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/solutions/136684/121-mai-mai-gu-piao-de-zui-jia-shi-ji-by-leetcode-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

【LeetCode】121. 买卖股票的最佳时机
121. 买卖股票的最佳时机 难度:简单 题目 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获…...
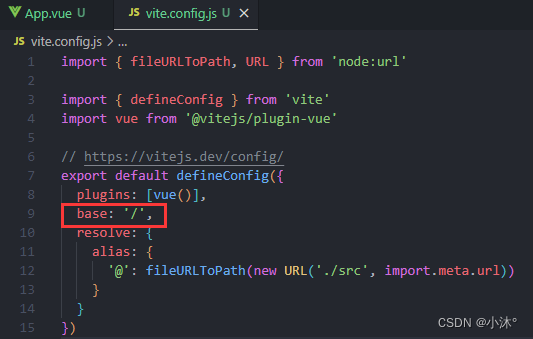
Vue3-VueRouter4路由语法解析
1.创建路由实例由createRouter实现 2.路由模式 1)history模式使用createWebHistory():地址栏不带# 2)hash模式使用createWebHashHistory():地址栏带# 3)参数是基础路径,默认/ 括号里的就是设置路径的前…...
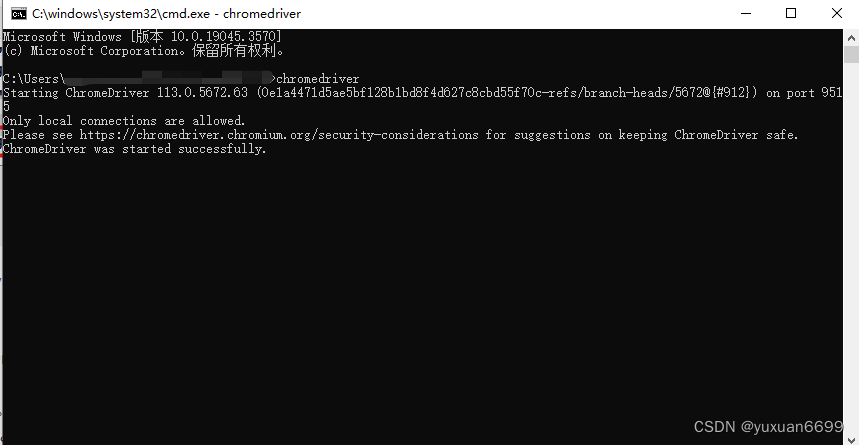
ChromeDriver最新版本下载与安装方法
关于ChromeDriver最新下载地址:https://googlechromelabs.github.io/chrome-for-testing/ 下载与安装 setp1:查看Chrome浏览器版本 首先,需要检查Chrome浏览器的版本。请按照以下步骤进行: 打开Chrome浏览器。 点击浏览器右上角…...
illuminate/database 使用 四
文档:Hyperf Database: Getting Started - Laravel 10.x - The PHP Framework For Web Artisans 因为hyperf使用illuminate/database,所以按照文章,看illuminate/database代码实现。 一、读写分离 根据文档读写的host可以分开。设置读写分…...
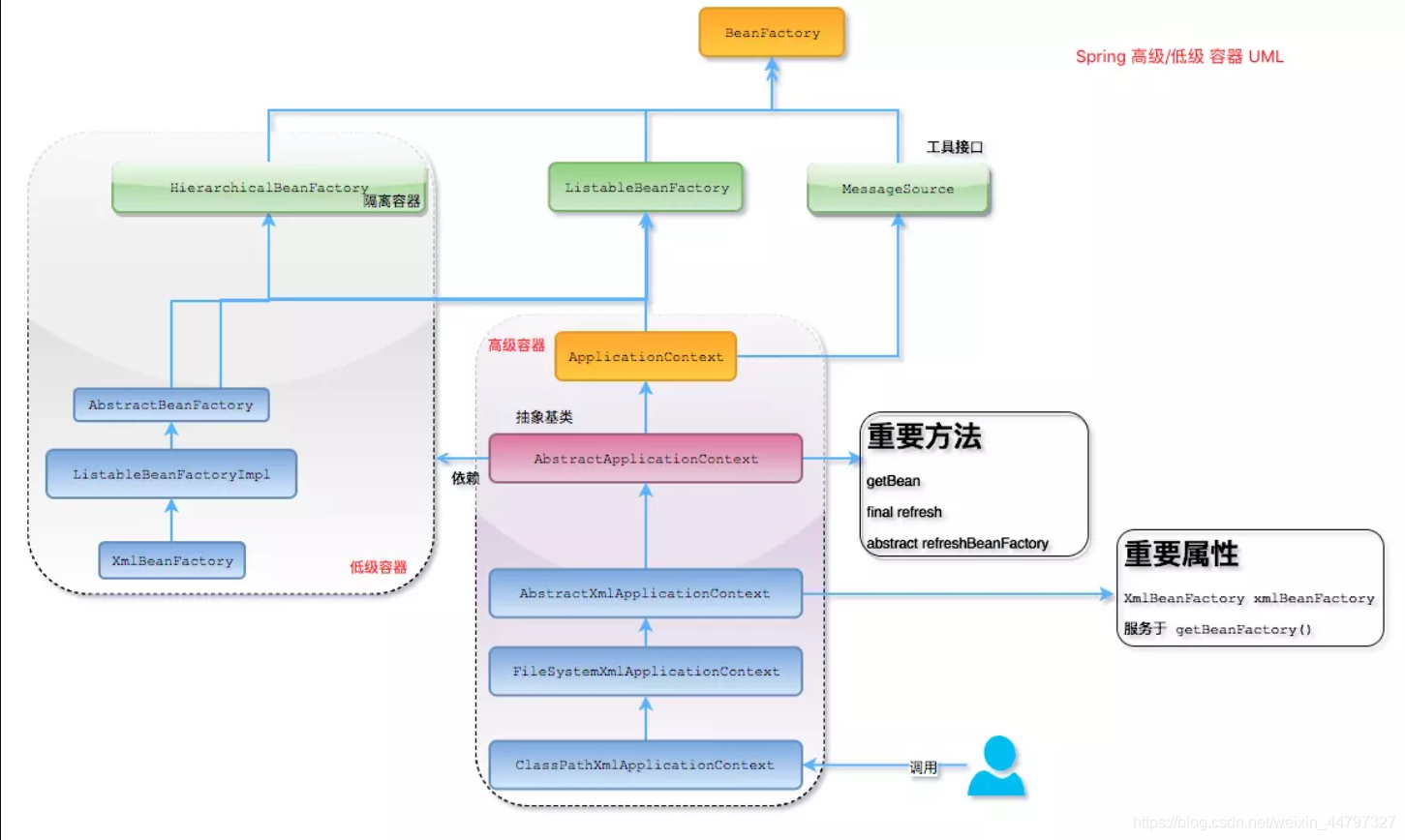
Spring面向切面编程(AOP);Spring控制反转(IOC);解释一下Spring AOP里面的几个名词;Spring 的 IoC支持哪些功能
文章目录 Spring面向切面编程(AOP)什么是AOPSpring AOP and AspectJ AOP 的区别?Spring AOP中的动态代理如何理解 Spring 中的代理?解释一下Spring AOP里面的几个名词Spring在运行时通知对象Spring切面可以应用5种类型的通知:什么是切面 Aspe…...

vatee万腾的科技征途:Vatee独特探索的数字化力量
在数字化时代的浪潮中,Vatee万腾以其独特的科技征途成为引领者。公司在数字化领域的探索之路不仅是技术的创新,更是一种对未知的勇敢涉足,是对新时代的深刻洞察和积极实践。 Vatee万腾通过独特的探索,展示了在数字化征途上的创新力…...

MySQL学习day03
一、SQL图形化界面工具 常用比较常用的图形化界面有sqlyog、mavicat、datagrip datagrip工具使用相当方便,功能比前面两种都要强大。 DataGrip工具的安装和使用请查看这篇文档:DataGrip 安装教程 DML-介绍 DML全称是Data Manipulation Language(数据…...

《QT从基础到进阶·三十七》QWidget实现左侧导航栏效果
NavigationBarPlugin插件类实现了对左侧导航栏的管理,我们可以在导航栏插件中添加界面,并用鼠标点击导航栏能够切换对应的界面。 源码在文章末尾 实现效果如下: NavigationBarPlugin实现的接口如下: class NAVIGATIONBAR_EXP…...

sftp学习
什么是sftp? sftp的简单操作 远程连接 int RobostSftp::Init(QString ip,QString port,QString user_name, QString user_password) { int rc;session ssh_new();if (!session) {fprintf(stderr, "ssh initialization failed\n");// return 1…...

C++之STL库:string类(用法列举和总结)
前言 大家在学习STL库的时候一定要学会看英文文档,俗话说熟能生巧,所以还得多练!在使用string类之前,要包含头文件#include <string>和using namespace std; 文档链接:string - C Reference 一、string——构造…...
小程序中的大道理--综述
前言 以下将用一个小程序来探讨一些大道理, 这些大道理包括可扩展性, 抽象与封装, 可维护性, 健壮性, 团队合作, 工具的利用, 可测试性, 自顶向下, 分而治之, 分层, 可读性, 模块化, 松耦合, MVC, 领域模型, 甚至对称性, 香农的信息论等等. 为什么不用大程序来说大道理呢? …...

tlais智能学习辅助系统-修改部门功能实现
学习黑马程序员的JavaWeb课程,自己写的部门信息修改部分程序 控制层: //DeptController.java /** * 根据ID查询部门信息 * param id * return */ GetMapping("/{id}") public Result select(PathVariable Integer id){log.info("查询id…...
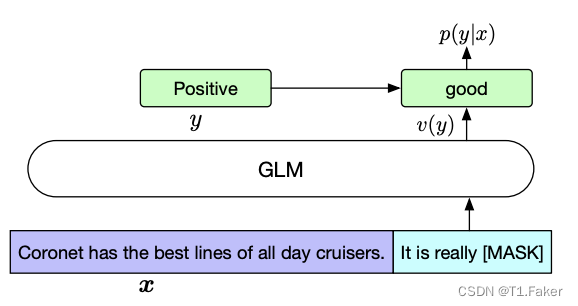
GLM: 自回归空白填充的多任务预训练语言模型
当前,ChatGLM-6B 在自然语言处理领域日益流行。其卓越的技术特点和强大的语言建模能力使其成为对话语言模型中的佼佼者。让我们深入了解 ChatGLM-6B 的技术特点,探索它在对话模型中的创新之处。 GLM: 自回归空白填充的多任务预训练语言模型 ChatGLM-6B 技…...

函数递归所应满足的条件
1.递归的概念 递归是学习C语⾔函数绕不开的⼀个话题,那什么是递归呢? 递归其实是⼀种解决问题的⽅法,在C语⾔中,递归就是函数⾃⼰调⽤⾃⼰。 递归的思想: 把⼀个⼤型复杂问题层层转化为⼀个与原问题相似,但…...

Python入职某新员工大量使用Lambda表达式,却被老员工喷是屎山
Python中Lambda表达式是一种简洁而强大的特性,其在开发中的使用优缺点明显,需要根据具体场景权衡取舍。 Lambda表达式的优点之一是它的紧凑语法,适用于一些短小而简单的函数。这种形式使得代码更为精炼,特别在一些函数式编程场景中,Lambda表达式可以提高代码的表达力。此外…...
Android Bitmap保存成至手机图片文件,Kotlin
Android Bitmap保存成至手机图片文件,Kotlin fun saveBitmap(name: String?, bm: Bitmap) {val savePath Environment.getExternalStoragePublicDirectory(Environment.DIRECTORY_PICTURES).toString()if (!Files.exists(Paths.get(savePath))) {Log.d("保存文…...
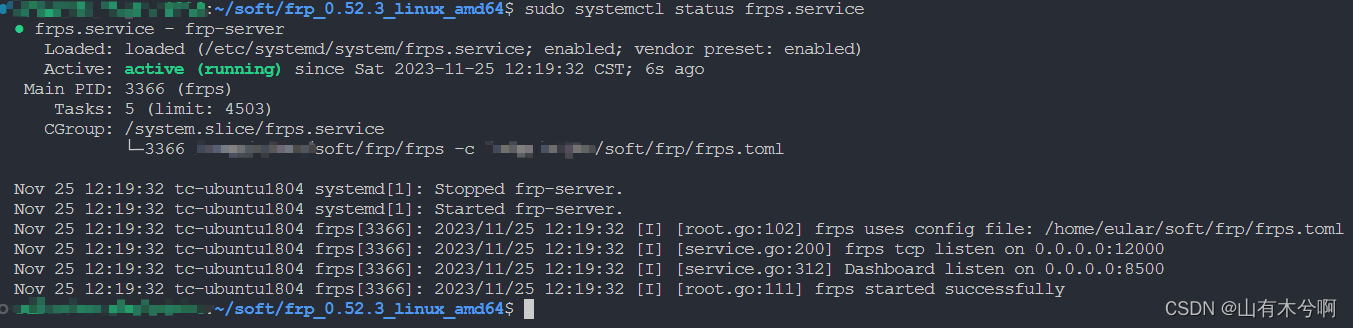
frp V0.52.3 搭建
下载 https://github.com/fatedier/frp/releases/ 此版本暂时没有windows的,想在windows使用请下载v0.52.2 简易搭建 frps.toml的配置文件,以下12000、8500需要在云服务器中的防火墙中开放tcp # bindPort为frps和frpc通信的端口,需要在防…...

最近数据分析面试的一点感悟...
我是阿粥,也是小z 最近面了不少应届的同学(数据分析岗位),颇有感触,与各位分享。 简历可以润色,但要适度 运用一些原则,如STAR法则,让简历逻辑更清晰,条块分明࿰…...
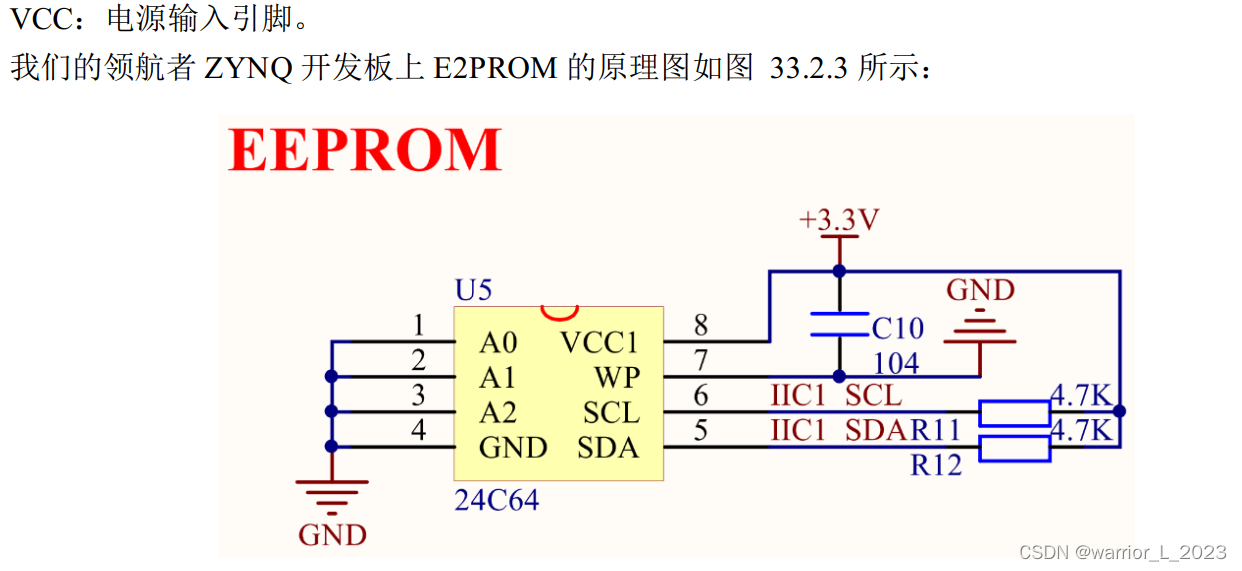
ZYNQ_project:IIC_EEPROM
EEPROM简介: EEPROM(Electrically Erasable Progammable Read Only Memory, E2PROM)是指带电可擦可编程只读存 储器,是一种常用的非易失性存储器(掉电数据不丢失), E2PROM 有多种类型的产品,我…...

Leetcode 2940. Find Building Where Alice and Bob Can Meet
Leetcode 2940. Find Building Where Alice and Bob Can Meet 1. 解题思路2. 代码实现3. 算法优化 题目链接:2940. Find Building Where Alice and Bob Can Meet 1. 解题思路 这一题本质上又是限制条件下求极值的问题,算是我最不喜欢的题目类型之一吧…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...
