人工智能|机器学习——感知器算法原理与python实现
感知器算法是一种可以直接得到线性判别函数的线性分类方法,它是基于样本线性可分的要求下使用的。
一、线性可分与线性不可分

为了方便讨论,我们蒋样本
增加了以为常数,得到增广样向量 y=(1;
;
;...;
),则n个样本的集合为(
,
;
,.....,
),增广权矢量表示为 a = (
;
;
....,
),我们得到新的怕没别函数


二、算法步骤

三、算法实现
1.生成数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets# 加载数据集
iris = datasets.load_iris()# 提取特征和目标变量
x = iris.data
y = iris.target# 只选择两个特征变量和两个目标类别,进行简单的二分类
x = x[y < 2, :2]
y = y[y < 2]# 绘制散点图
plt.scatter(x[y == 0, 0], x[y == 0, 1]) # 绘制类别0的样本
plt.scatter(x[y == 1, 0], x[y == 1, 1]) # 绘制类别1的样本
plt.show()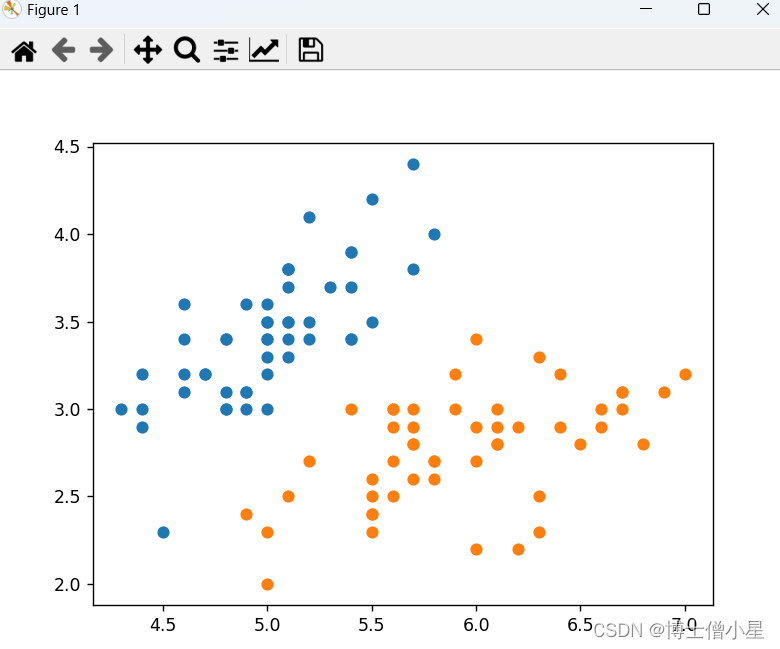
2.实现算法
def check(w, x, y):# 检查预测结果是否与真实标签一致return ((w.dot(x.T)>0).astype(int)==y).all() def train(w, train_x, train_y, learn=1, max_iter=200):iter = 0while ~check(w, train_x, train_y) and iter<=max_iter:iter += 1for i in range(train_y.size):predict_y = (w.dot(train_x[i].T)>0).astype(int)if predict_y != train_y[i]:# 根据预测和真实标签的差异调整权重w += learn*(train_y[i] - predict_y)*train_x[i]return wdef normalize(x):# 归一化函数,将输入数据转换到0-1范围max_x = np.max(x, axis=0)min_x = np.min(x, axis=0)norm_x = (max_x - x) / (max_x - min_x)return norm_xnorm_x = normalize(x)
train_x = np.insert(norm_x, 0, values=np.ones(100).T, axis=1)
w = np.random.random(3)
w = train(w, train_x, y)3.绘制决策边界
def plot_decision_boundary(w, axis):# 生成决策边界的坐标网格x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1))x_new = np.c_[x0.ravel(), x1.ravel()]x_new = np.insert(x_new, 0, np.ones(x_new.shape[0]), axis=1)# 对网格中的点进行预测y_predict = (w.dot(x_new.T)>0).astype(int)zz = y_predict.reshape(x0.shape)# 设置自定义的颜色映射from matplotlib.colors import ListedColormapcustom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])# 绘制决策边界plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)# 绘制决策边界
plot_decision_boundary(w, axis=[-1, 1, -1, 1])
# 绘制类别为0的样本点(红色)
plt.scatter(norm_x[y==0, 0], norm_x[y==0, 1], color='red')
# 绘制类别为1的样本点(蓝色)
plt.scatter(norm_x[y==1, 0], norm_x[y==1, 1], color='blue')
# 显示图形
plt.show()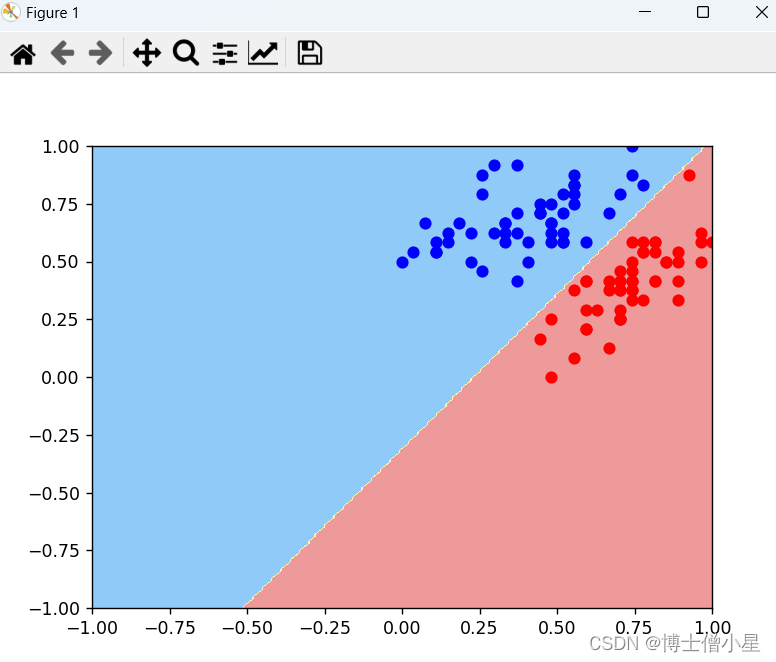
4.使用sklearn库完成算法
from sklearn.datasets import make_classificationx,y = make_classification(n_samples=1000, n_features=2,n_redundant=0,n_informative=1,n_clusters_per_class=1)#n_samples:生成样本的数量#n_features=2:生成样本的特征数,特征数=n_informative() + n_redundant + n_repeated#n_informative:多信息特征的个数#n_redundant:冗余信息,informative特征的随机线性组合#n_clusters_per_class :某一个类别是由几个cluster构成的 #训练数据和测试数据
x_data_train = x[:800,:]
x_data_test = x[800:,:]
y_data_train = y[:800]
y_data_test = y[800:]#正例和反例
positive_x1 = [x[i,0] for i in range(1000) if y[i] == 1]
positive_x2 = [x[i,1] for i in range(1000) if y[i] == 1]
negetive_x1 = [x[i,0] for i in range(1000) if y[i] == 0]
negetive_x2 = [x[i,1] for i in range(1000) if y[i] == 0]
from sklearn.linear_model import Perceptron
#定义感知机
clf = Perceptron(fit_intercept=False,shuffle=False)
#使用训练数据进行训练
clf.fit(x_data_train,y_data_train)
#得到训练结果,权重矩阵
print(clf.coef_)
#输出为:[[-0.38478876,4.41537463]]#超平面的截距,此处输出为:[0.]
print(clf.intercept_)#利用测试数据进行验证
acc = clf.score(x_data_test,y_data_test)
print(acc)
#得到的输出结果为0.98,这个结果还不错吧。
from matplotlib import pyplot as plt
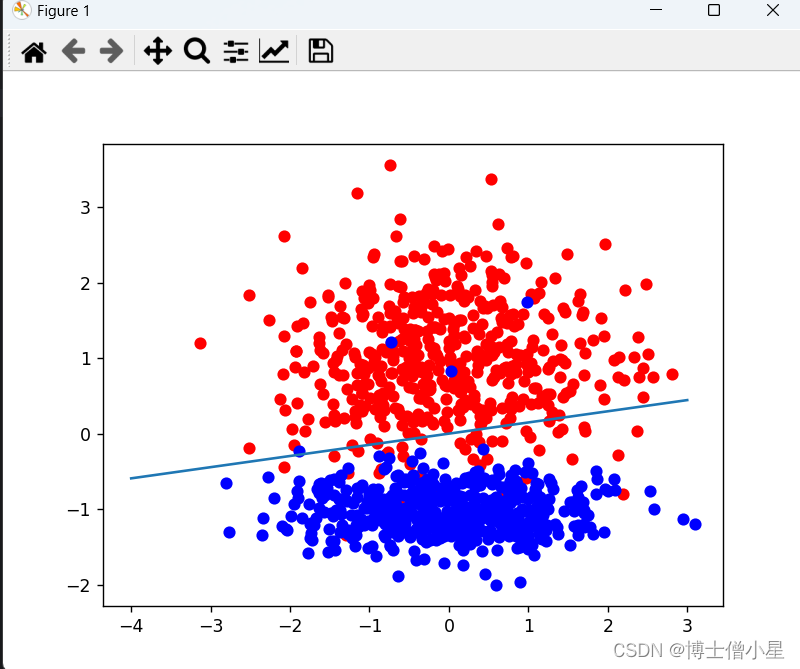
#画出正例和反例的散点图
plt.scatter(positive_x1,positive_x2,c='red')
plt.scatter(negetive_x1,negetive_x2,c='blue')
#画出超平面(在本例中即是一条直线)
line_x = np.arange(-4,4)
line_y = line_x * (-clf.coef_[0][0] / clf.coef_[0][1]) - clf.intercept_
plt.plot(line_x,line_y)
plt.show()四、优缺点
1.优点:
简单且易于实现:感知器算法是一种简单而有效的分类算法,它的基本原理易于理解,实现也相对简单。
收敛性保证:如果数据集是线性可分的,感知器算法可以收敛到最优解,即找到将不同类别分开的最优超平面。
适用于大型数据集:感知器算法具有较好的可扩展性,对于大型数据集也能够有效处理。
2缺点:
仅适用于线性可分问题:感知器算法只能处理线性可分的问题,当数据集不满足线性可分条件时,算法不能收敛到最优解。
对初始权重敏感:感知器算法的收敛性与初始权重的选择有关,较差的初始权重选择可能导致算法无法收敛或者收敛到较差的分类结果。
无法处理非线性问题:感知器算法无法处理非线性的分类问题,对于非线性数据集,需要使用更复杂的分类算法或者考虑使用特征转换等技术。
只能进行二分类:感知器算法只能进行二分类,无法直接处理多分类问题,需要通过拓展或组合多个感知器来处理多分类任务。
总体而言,感知器算法是一种简单而有效的线性分类算法,适用于处理线性可分的二分类问题。然而,对于非线性问题或者多分类问题,感知器算法存在一些局限性,需要使用其他更复杂的算法来解决。
相关文章:
人工智能|机器学习——感知器算法原理与python实现
感知器算法是一种可以直接得到线性判别函数的线性分类方法,它是基于样本线性可分的要求下使用的。 一、线性可分与线性不可分 为了方便讨论,我们蒋样本增加了以为常数,得到增广样向量 y(1;;;...;),则n个样本的集合为&a…...

【论文阅读笔记】Prompt-to-Prompt Image Editing with Cross-Attention Control
【论文阅读笔记】Prompt-to-Prompt Image Editing with Cross-Attention Control 个人理解思考基本信息摘要背景挑战方法结果 引言方法论结果讨论引用 个人理解 通过将caption的注意力图注入到目标caption注意力中影响去噪过程以一种直观和便于理解的形式通过修改交叉注意力的…...
Echarts legend图例配置项 设置位置 显示隐藏
Echarts 官网完整配置项 https://echarts.apache.org/zh/option.html#legend 配置项 legend: { }设置图例为圆形 icon: circle,//设置图例为圆形设置图例位置 top: 20%//距离顶部百分之20//y:bottom 在底部显示设置图例 宽度 高度 itemWidth: 10,//设置图例宽度 itemHeight: …...

C#每天复习一个重要小知识day3:随机数的生成
目录 格式: 生成随机数: 生成一个0-100的随机数: 以下是更详细的代码示例: 在C#中,可以使用Random类来生成随机数。这个类提供了多种方法来生成不同类型的随机数。 格式: Random 随机变量名(r) new …...

Java后端使用XWPFDocument生成word文档,踩坑
以下都是借鉴网上内容: 环境 纯后端, java, spring项目 maven管理. maven内容: <dependency><groupId>org.apache.poi</groupId><artifactId>poi-ooxml</artifactId><version>3.16</version></dependency><dependency>…...

asp.net core HttpContextAccessor类
在 ASP.NET Core 中 ,HttpContextAccessor 是一个用于访问当前 HTTP 请求的工具类。它通常用于在应用程序中获取当前 HTTP 请求的上下文信息,例如请求的路由、头部信息、用户身份验证状态等。 HttpContextAccessor 类通常在需要访问当前 HTTP 请求上下文…...
微服务--04--SpringCloudGateway 网关
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.网关路由1.1 认识网关在SpringCloud当中,提供了两种网关实现方案: 1.2.快速入门1.3.路由过滤 2.网关登录校验2.1.鉴权思路分析2.2.网关过滤…...
Java程序连接 nacos集群
我们在bootstrap.yml文件里可以直接连一个nacos集群的. 架构如下 没错,我们程序直连的是通过Nginx的,利用nginx的反向代理来做到连接nacos集群. 我们先把nginx的配置贴上来 upstream cluster{server 127.0.0.1:8848;server 127.0.0.1:8849;server 127.0.0.1:8850; }server{l…...
【深度学习】参数优化和训练技巧
寻找合适的学习率(learning rate) 学习率是一个非常非常重要的超参数,这个参数呢,面对不同规模、不同batch-size、不同优化方式、不同数据集,其最合适的值都是不确定的,我们无法光凭经验来准确地确定lr的值,我们唯一可…...

CeresPCL 曲线拟合之三次多项式
文章目录 一、简介2.1 实现步骤二、实现代码三、实现效果参考资料一、简介 2.1 实现步骤 (1)构建代价函数。假设我们得到了一组数据,也知晓该数据是用曲线方程: y = a x 3 + b x 2 + c x +...

小白备战蓝桥杯:Java基础语法
一、注释 IDEA注释快捷键:Ctrl / 单行注释: //注释信息 多行注释: /* 注释信息 */ 二、字面量 常用数据:整数、小数、字符串(双引号)、字符(单引号)、布尔值(tr…...

C#面向对象
过程类似函数只能执行没有返回值 函数不仅能执行,还可以返回结果 1、面向过程 a 把完成某一需求的所有步骤 从头到尾 逐步实现 b 根据开发需求,将某些 功能独立 的代码 封装 成一个又一个 函数 c 最后完成的代码就是顺序的调用不同的函数 特点 1、…...

智能优化算法应用:基于蝙蝠算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝙蝠算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蝙蝠算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蝙蝠算法4.实验参数设定5.算法结果6.参考文献7.MATLAB…...
【栈和队列(1)(逆波兰表达式)】
文章目录 前言什么是栈(Stack)栈方法栈的模拟实现链表也可以实现栈逆波兰表达式逆波兰表达式在栈中怎么使用 前言 什么是栈(Stack) 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶࿰…...
Blazor Table 实现获取当前选中行的功能
这里需要使用到OnClickRowCallBack事件 后台使用案例...
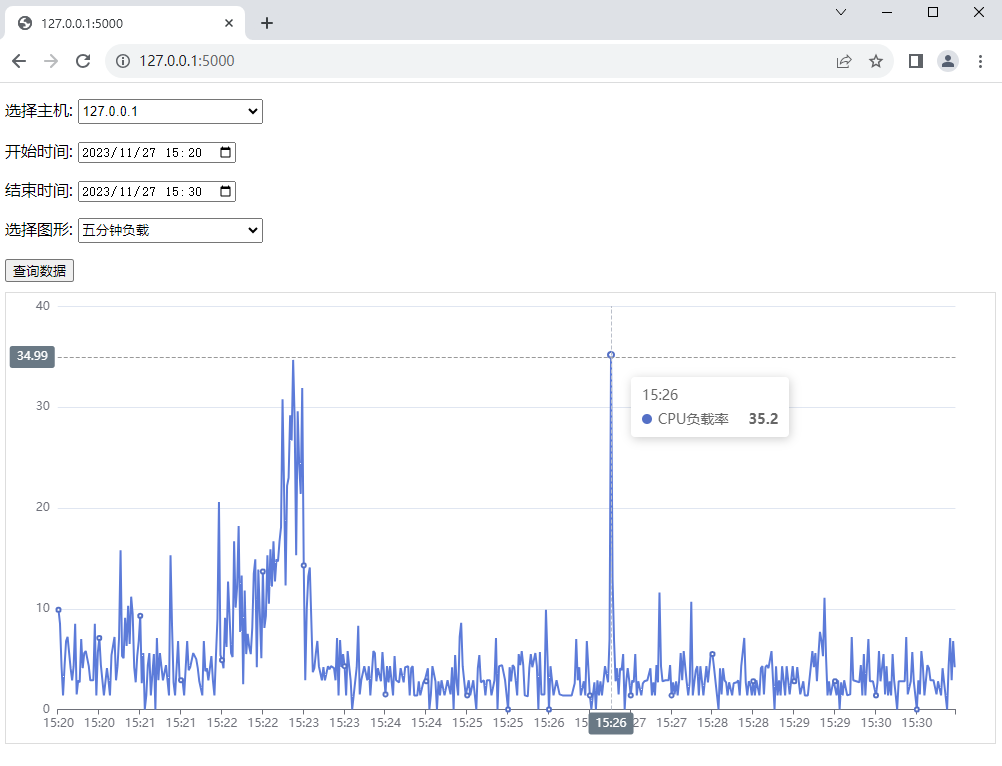
Flask Echarts 实现历史图形查询
Flask前后端数据动态交互涉及用户界面与服务器之间的灵活数据传递。用户界面使用ECharts图形库实时渲染数据。它提供了丰富多彩、交互性强的图表和地图,能够在网页上直观、生动地展示数据。ECharts支持各种常见的图表类型,包括折线图、柱状图、饼图、散点…...

【漫谈】信创
近些年来,自主创新绝对是高频词汇。 以往是供应链、芯片领域,现在终于到了信息领域。 近期,从上至下、从中央到地方、从政府到国企,各层面、各行业、各领域都在提及“信创”。 信创是个大工程,从计算机通用处理器、…...

linux wget --no-check-certificate
如果您希望每次使用wget命令时都跳过SSL证书检查,可以将–no-check-certificate参数添加到wget的默认配置文件中。 请按照以下步骤进行操作: vi ~/.wgetrc# 插入内容 check_certificate off保存并关闭文件。 现在,wget命令将在每次使用时自…...

mysql命令行连接数据库
有时项目连接不上数据库,报错鉴权失败,先用mysql工具连接下,容易发现问题。 直接输入mysql看是否已安装,如果没有就安装下。 # 注:直接mysql就行,不用-cli也不用-client,也不用-server…...

计算机丢失vcomp140.dll是什么意思,如何解决与修复(附教程)
vcomp140.dll缺失的5种解决方法以及vcomp140.dll缺失原因 引言: 在日常使用电脑的过程中,我们可能会遇到一些错误提示,其中之一就是“vcomp140.dll缺失”。这个错误提示通常出现在运行某些程序或游戏时,给使用者带来了困扰。本文…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
