leetcode每日一题35
90. 子集 II
回溯嘛
子集啊排列组合啊棋盘啊都是回溯
回溯三部曲走起
跟78.子集比,本题给出的数组里存在重复元素了
所以在取元素时,如果同一层里取过某个元素,那么在该层就不能取重复的该元素了
如给出的数组[1,2,2]
可以在某一次递归中第一个取2放进子集,但后面的递归就不允许第一个取2放进子集里了
详情可以看代码随想录的图
代码随想录
所以要有一个数组used记录该层里取过的数
- 递归函数参数
回溯问题一般涉及两个全局变量:
保存本次递归中符合条件的结果path
保存所有符合条件的结果的集合result
以及回溯函数backtracking,因为是求子集问题,所以取过的元素不能重复取,所以回溯时,for循环要从startIndex开始,而不是从0开始
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used)
- 递归终止条件
当此时的startIndex已经大于数组长度时,就没有没取过的数组元素了,本次递归就终止了
if(startIndex>=nums.size()){return;
}
- 单层搜索逻辑
单层的搜索逻辑是
先将取出来的数存入path,再递归调用自身,然后回溯,删掉刚才取出来的数
path.push_back(nums[i]);
backtracking(……);
path.pop_back();
本题中,要判断取的nums[i]有没有使用过
如果没有,那么在backtracking要传入used数组,所以要递归前标记nums[i]已经被使用过了而递归后,需要回溯,从path中删除nums[i],所以要恢复为nums[i]未被使用
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;
}//判定nums[i]有没有使用过
path.push_back(nums[i]);
used[i]=true;
backtracking(nums, i+1,used);
used[i]=false;
path.pop_back();
所以,回溯算法模板为
void backtracking(参数) {收集子集result.push_back(path);if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
那么组合起来,本题的回溯函数为
vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used){result.push_back(path);//收集子集if(startIndex>=nums.size()){return;}for(int i =startIndex;i<nums.size();i++){if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}//判定nums[i]有没有使用过path.push_back(nums[i]);used[i]=true;backtracking(nums, i+1,used);used[i]=false;path.pop_back();}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0, used);return result;}
整理一下,得到最终代码:
class Solution {
private:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& nums, int startIndex, vector<bool>& used){result.push_back(path);//收集子集,要放在判定停止条件前,防止漏数if(startIndex>=nums.size()){return;}for(int i =startIndex;i<nums.size();i++){if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}//判定nums[i]有没有使用过path.push_back(nums[i]);used[i]=true;backtracking(nums, i+1,used);used[i]=false;path.pop_back();}}
public:vector<vector<int>> subsetsWithDup(vector<int>& nums) {result.clear();path.clear();vector<bool> used(nums.size(), false);sort(nums.begin(), nums.end()); // 去重需要排序backtracking(nums, 0, used);return result;}
};
相关文章:

leetcode每日一题35
90. 子集 II 回溯嘛 子集啊排列组合啊棋盘啊都是回溯 回溯三部曲走起 跟78.子集比,本题给出的数组里存在重复元素了 所以在取元素时,如果同一层里取过某个元素,那么在该层就不能取重复的该元素了 如给出的数组[1,2,2] 可以在某一次递归中第一…...
第二十章——多线程
一.线程简介 线程的特点 1.进程是资源分配的最小单位,线程是最小的执行单位 2.一个进程可以有多个线程 3.线程共享进程资源 二.创建线程 1.继承Thread类 1.Thread类是java.lang包中的一个类,从这个类实例化的对象代表线程,程序员启动一个新…...

【FGPA】Verilog:JK 触发器 | D 触发器 | T 触发器 | D 触发器的实现
0x00 JK 触发器 JK 触发器是 RS 触发器和 T 触发器的组合,有两个输入端 J 和 K,如果两个输入端都等于 1,则将当前值反转。 行为表 状态图 Timing Diagram Circuit JK 触发器的设计目的是防止 RS 触发器在输入 S 和 R 均等于 …...
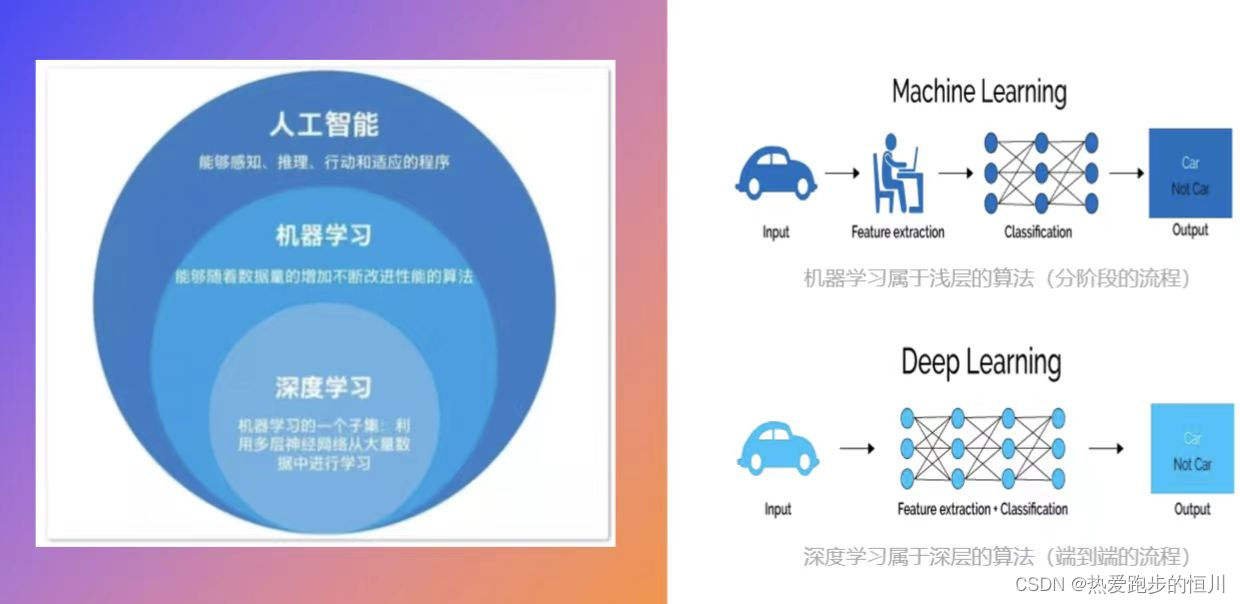
【人工智能】人工智能的技术研究与安全问题的深入讨论
前言 人工智能(Artificial Intelligence),英文缩写为AI。 它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。人工智能是新一轮科技革命和产业变革的重要驱动力量。 📕作者简介&#x…...
苹果提醒事项怎么用?几个简单步骤就能学会!
苹果提醒事项可以帮助你轻松管理待办事项,让你更好地安排自己的时间和工作。但是,有些小伙伴可能对如何使用这个功能还有一些疑问。苹果提醒事项怎么用?不要担心,小编将为大家提供使用提醒事项的方法,帮助你学会如何使…...

<HarmonyOS第一课>从简单的页面开始 【课后考核】
判断题 在Column容器中的子组件默认是按照从上到下的垂直方向布局的,其主轴的方向是垂直方向,在Row容器中的组件默认是按照从左到右的水平方向布局的,其主轴的方向是水平方向。 正确(True)List容器可以沿水平方向排列,也可以沿垂…...

如何实现按需加载
如何实现按需加载 实现按需引入的步骤: ES6模块语法: 确保你的组件库使用了ES6模块语法,这是按需引入的基础。 拆分组件: 将组件库拆分成独立的模块,每个模块包含一个组件。这样,只有需要的组件才会被引入…...

Vue3-admin-template的表格合计计算
直接上代码: <el-table:data"lists"style"width: 100%"max-height"500":header-cell-style"{ textAlign: center }":cell-style"{ textAlign: center }"show-summary:summary-method"getSummaries"…...

spring JdbcTemplate 快速入门
概述 Spring JDBC Template 是 Spring Framework 提供的一个简化 JDBC 操作的模板类。它封装了一些常见的 JDBC 操作,使得开发者在使用 JDBC 时能够更加便捷、简洁,同时也提供了异常处理和资源管理等功能。 导入pom 使用C3P0作为数据源 <project x…...
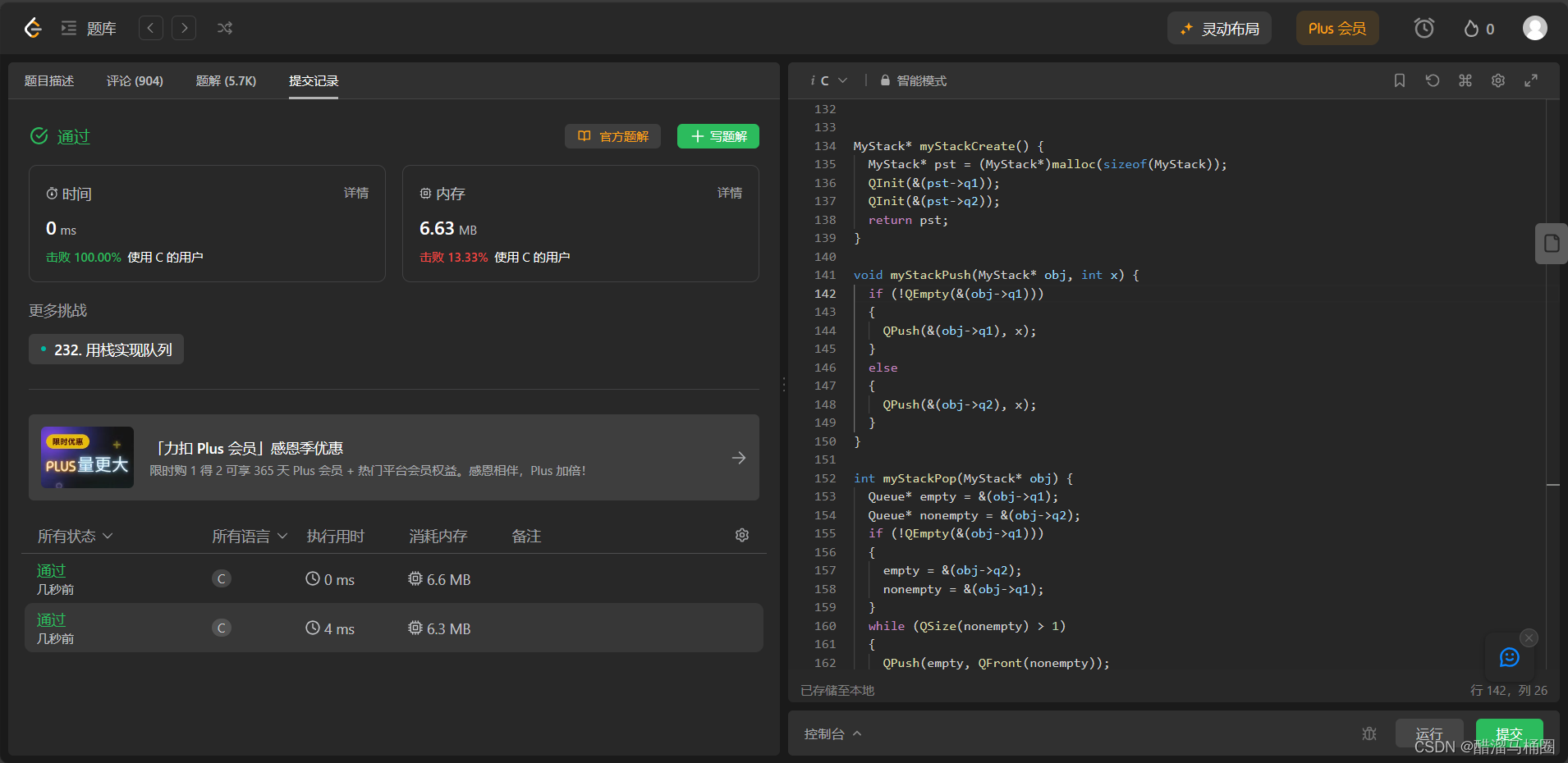
leetcode:用队列实现栈(后进先出)
题目描述 题目链接:225. 用队列实现栈 - 力扣(LeetCode) 题目分析 我们先把之前写的队列实现代码搬过来 用队列实现栈最主要的是实现栈后进先出的特点,而队列的特点是先进先出,那么我们可以用两个队列来实现 一个队…...

使用opencv实现更换证件照背景颜色
1 概述 生活中经常要用到各种要求的证件照电子版,红底,蓝底,白底等,大部分情况我们只有其中一种,本文通过opencv实现证件照背景的颜色替换。 1.1 opencv介绍 OpenCV(Open Source Computer Vision Librar…...
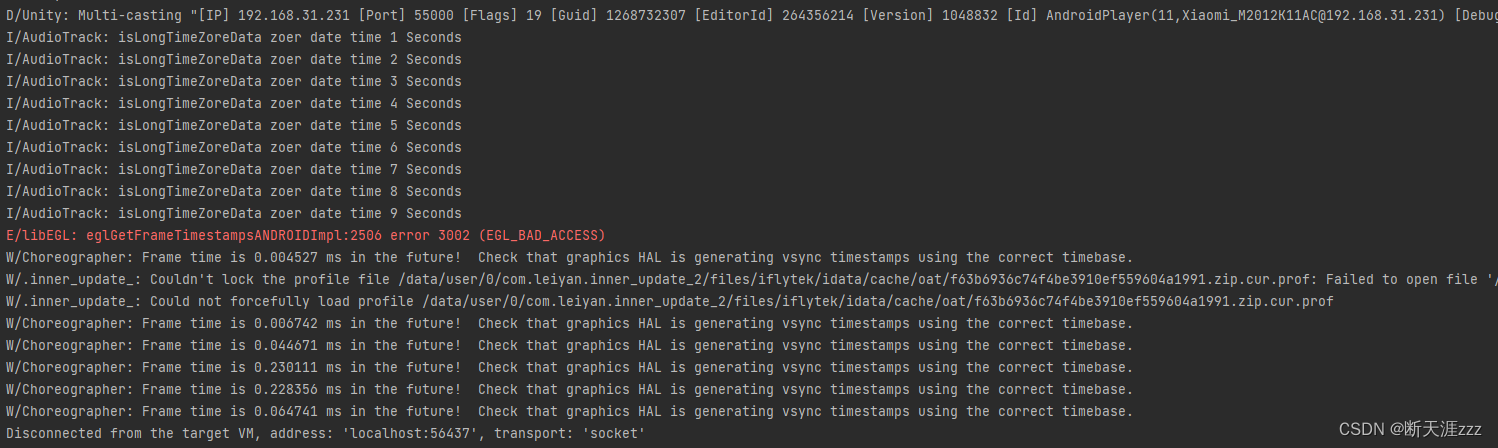
Unity打出的安卓包切换后台再恢复前台,卡顿许久问题记录
连接AndroidStudio发现当切换后台时提示:D/Unity: Multi-casting "[IP] 192.168.31.231 [Port] 55000 [Flags] 19 [Guid] 1268732307 [EditorId] 264356214 [Version] 1048832 [Id] AndroidPlayer(11,Xiaomi_M2012K11AC192.168.31.231) [Debug] 0 [PackageName…...

Linux常用命令----shutdown命令
文章目录 命令概述参数解释使用示例及解释 命令概述 shutdown 命令用于安全地关闭或重启 Linux 系统。它允许管理员指定一个时间点执行操作,并可发送警告信息给所有登录的用户。 参数解释 时间参数 ([时间]): now: 立即执行关闭或重启操作。m: 在 m 分钟后执行操作…...

美创科技受邀亮相第二届全球数字贸易博览会
11月23日-27日,由浙江省人民政府、商务部共同主办的第二届全球数字贸易博览会(以下简称“数贸会”)圆满落幕。围绕“国家级、国际性、数贸味”的目标定位,以“数字贸易 商通全球”为主题,数贸会重点展示数字贸易全产业…...

有n件物品,每件物品都有一个花费,要求每m个中必须至少选2个,求最小花费
题目 #include<bits/stdc.h> using namespace std; #define int long long #pragma GCC optimize(2) const int maxn 2e4 5, maxm 2e3 5, inf 1e9; int a[maxn]; int f[maxm][maxm];//f[i][j]表示选了第i个,上一个选的是第i-j个(每m个中选2个…...
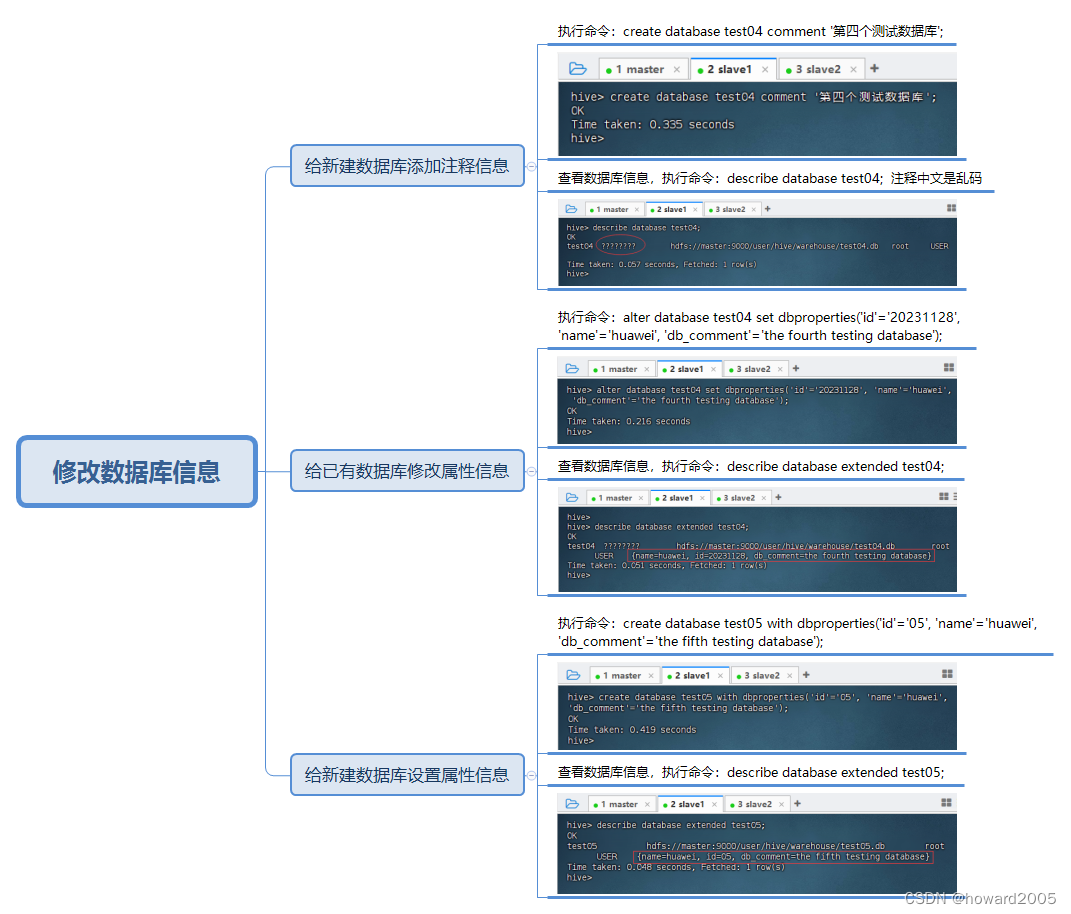
Hive数据库与表操作
文章目录 一、准备工作二、Hive数据库操作(一)Hive数据存储(二)创建数据库(三)查看数据库(四)修改数据库信息 一、准备工作 二、Hive数据库操作 (一)Hive数据…...

C语言数据结构之顺序表(上)
前言: ⭐️此篇博文主要分享博主在学习C语言的数据结构之顺序表的知识点时写的笔记,若有错误,还请佬指出,一定感谢!制作不易,若觉得内容不错可以点赞👍收藏❤️,这是对博主最大的认可…...
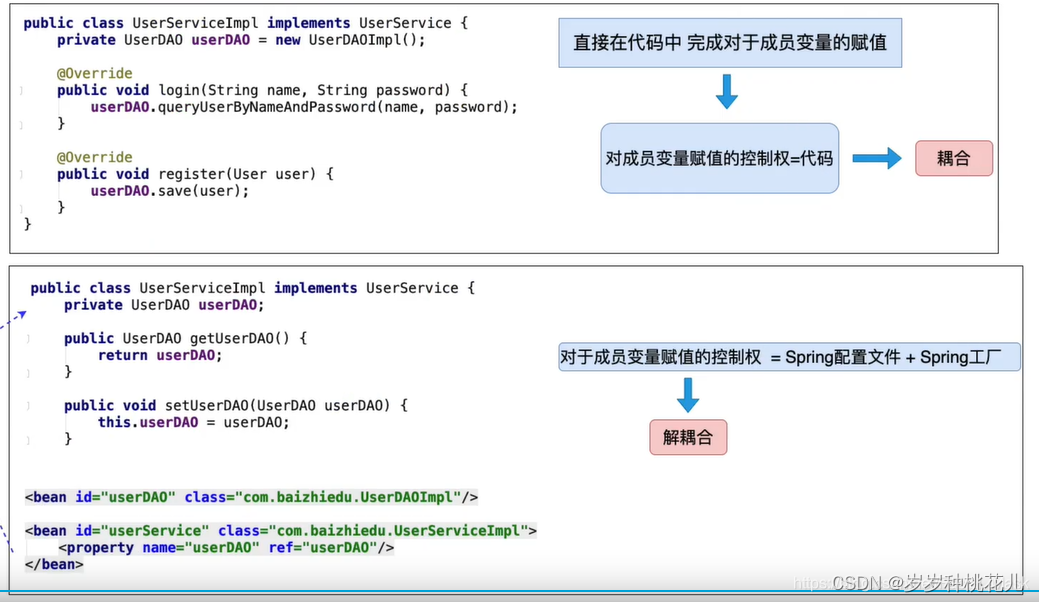
详解原生Spring中的控制反转和依赖注入-构造注入和Set注入
😉😉 学习交流群: ✅✅1:这是孙哥suns给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Mybatis、Spring...应用和源码级别的视频资料 🥭🥭3:QQ群:583783…...

数组中的第 K 个最大元素(C++实现)
数组中的第 K 个最大元素 题目思路代码 题目 数组中的第 K 个最大元素 思路 通过使用优先队列(最大堆)来找到数组中第k大的元素。通过弹出最大堆中的前k-1个元素,留下堆中的顶部元素作为结果返回。 代码 class Solution { public:int find…...
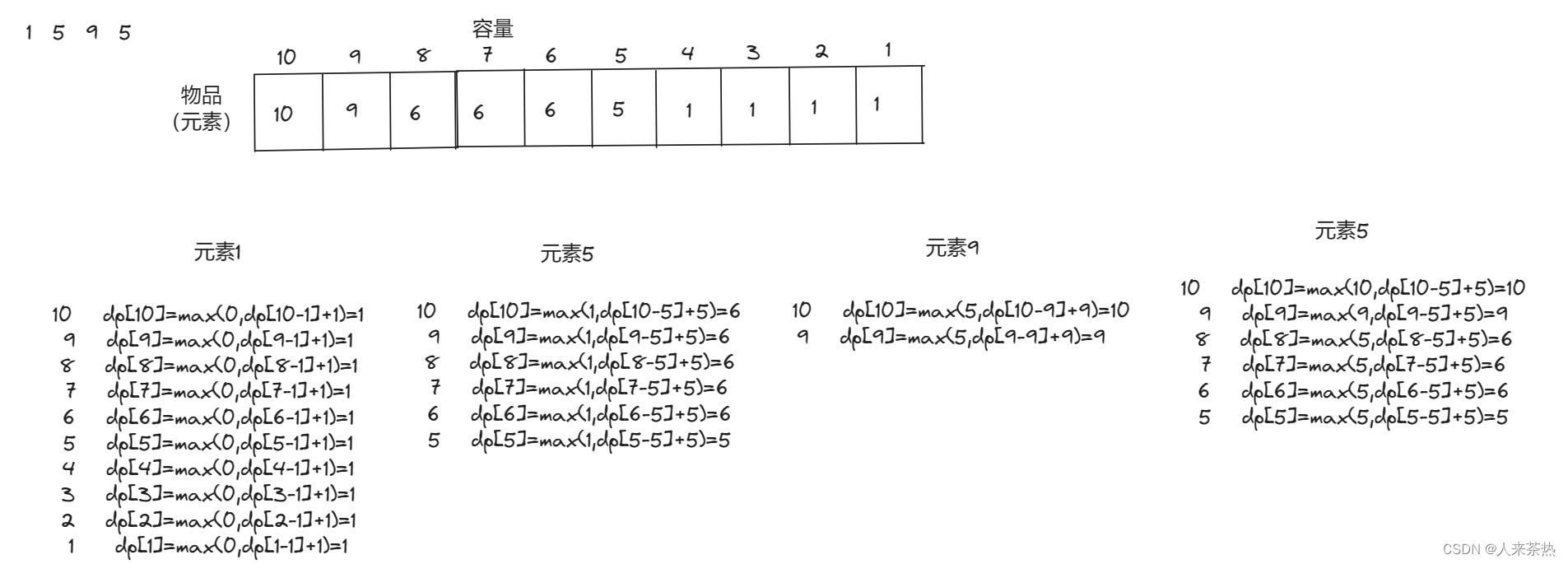
C++ day42背包理论基础01 + 滚动数组
背包问题的重中之重是01背包 01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 每一件物品其实只有两个状态,取或者不…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
