leetcode:2549. 统计桌面上的不同数字(python3解法)
难度:简单
给你一个正整数
n,开始时,它放在桌面上。在109天内,每天都要执行下述步骤:
- 对于出现在桌面上的每个数字
x,找出符合1 <= i <= n且满足x % i == 1的所有数字i。- 然后,将这些数字放在桌面上。
返回在
109天之后,出现在桌面上的 不同 整数的数目。注意:
- 一旦数字放在桌面上,则会一直保留直到结束。
%表示取余运算。例如,14 % 3等于2。示例 1:
输入:n = 5 输出:4 解释:最开始,5 在桌面上。 第二天,2 和 4 也出现在桌面上,因为 5 % 2 == 1 且 5 % 4 == 1 。 再过一天 3 也出现在桌面上,因为 4 % 3 == 1 。 在十亿天结束时,桌面上的不同数字有 2 、3 、4 、5 。示例 2:
输入:n = 3 输出:2 解释: 因为 3 % 2 == 1 ,2 也出现在桌面上。 在十亿天结束时,桌面上的不同数字只有两个:2 和 3 。提示:
1 <= n <= 100
题解:class Solution(object):def distinctIntegers(self, n):res = []res.append(n)for i in range(1,n+1):if n % i == 1:res.append(i)for j in res:for s in range(1,j):if j % s == 1 and s not in res:res.append(s) return len(res)
相关文章:
leetcode:2549. 统计桌面上的不同数字(python3解法)
难度:简单 给你一个正整数 n ,开始时,它放在桌面上。在 109 天内,每天都要执行下述步骤: 对于出现在桌面上的每个数字 x ,找出符合 1 < i < n 且满足 x % i 1 的所有数字 i 。然后,将这些…...

数据结构 / day03作业
1.顺序表按元素删除 //main.c#include "head.h" int main(int argc, const char *argv[]) {sqlist *listcreate_space();// printf("&list%p\n", list);int n;int index;data_type element, key;printf("please input n;");scanf("%d&…...

异步爬虫提速实践-在Scrapy中使用Aiohttp/Trio
在构建爬虫系统时,提高爬虫速度是一个关键问题。而使用异步爬虫技术可以显著提升爬取效率。在本文中,我将与大家分享如何在Scrapy中利用Aiohttp或Trio库实现异步爬取,以加快爬虫的速度。让我们开始吧! 1. 安装所需的库 首先&…...

Python与设计模式--访问者模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
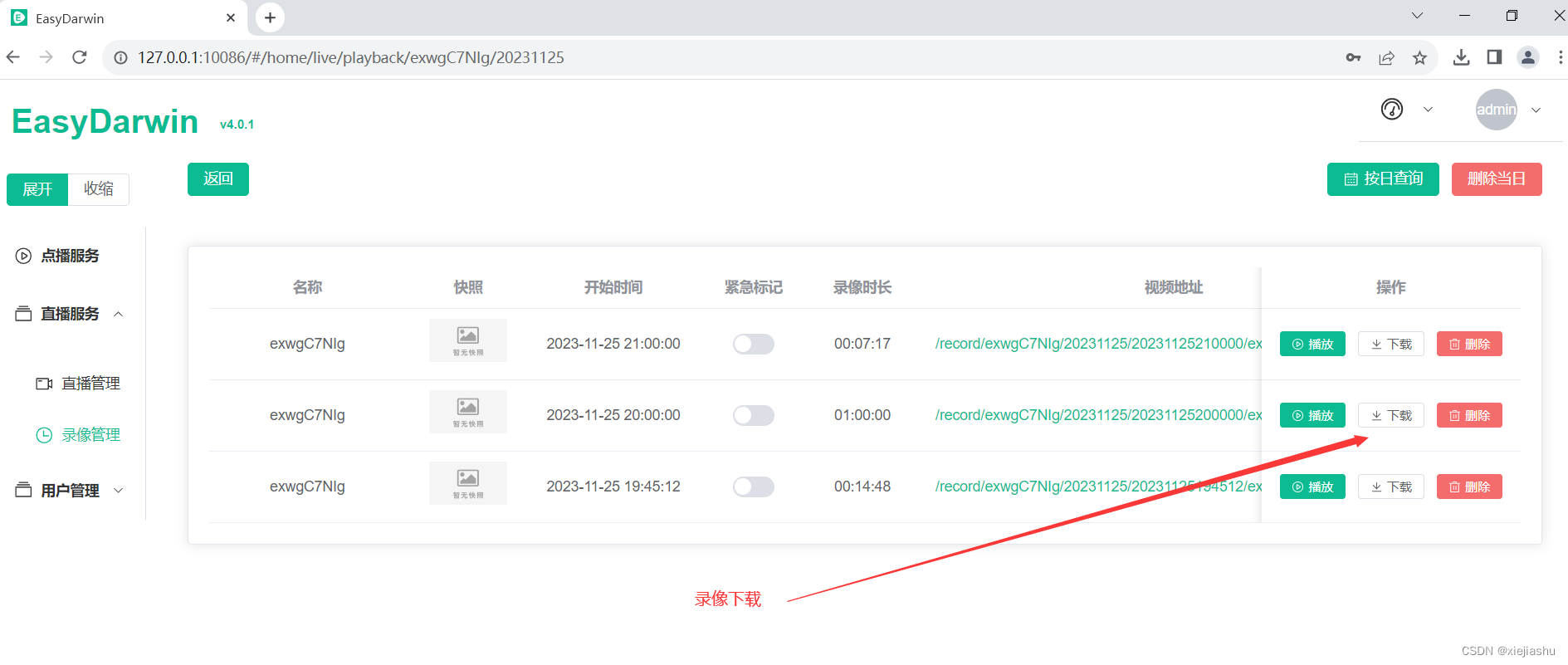
为社会做贡献的EasyDarwin 4.0.1发布了,支持视频点播、文件直播、摄像机直播、直播录像、直播回放、录像MP4合成下载
经过几个月的不懈努力和测试,最新的EasyDarwin 4.0版本总算是发布出来了,功能还是老几样:文件点播、视频直播(支持各种视频源)、直播录像与回放、录像合成MP4下载,稍稍看一下细节: 文件上传与点…...

CG向量和矩阵元素的获取
swizzle swizzle可以获取向量分量值;表现形式是点符号和rgba或xyzw rgba一般用作颜色表示 xyzw一般用于坐标表示分量值可以进行组合 例如:fixed4 test(1,2,3,4) 获取分量值:test.r 获取第一个分量值、test.g、test.xy、test.yx 向量维度转换…...
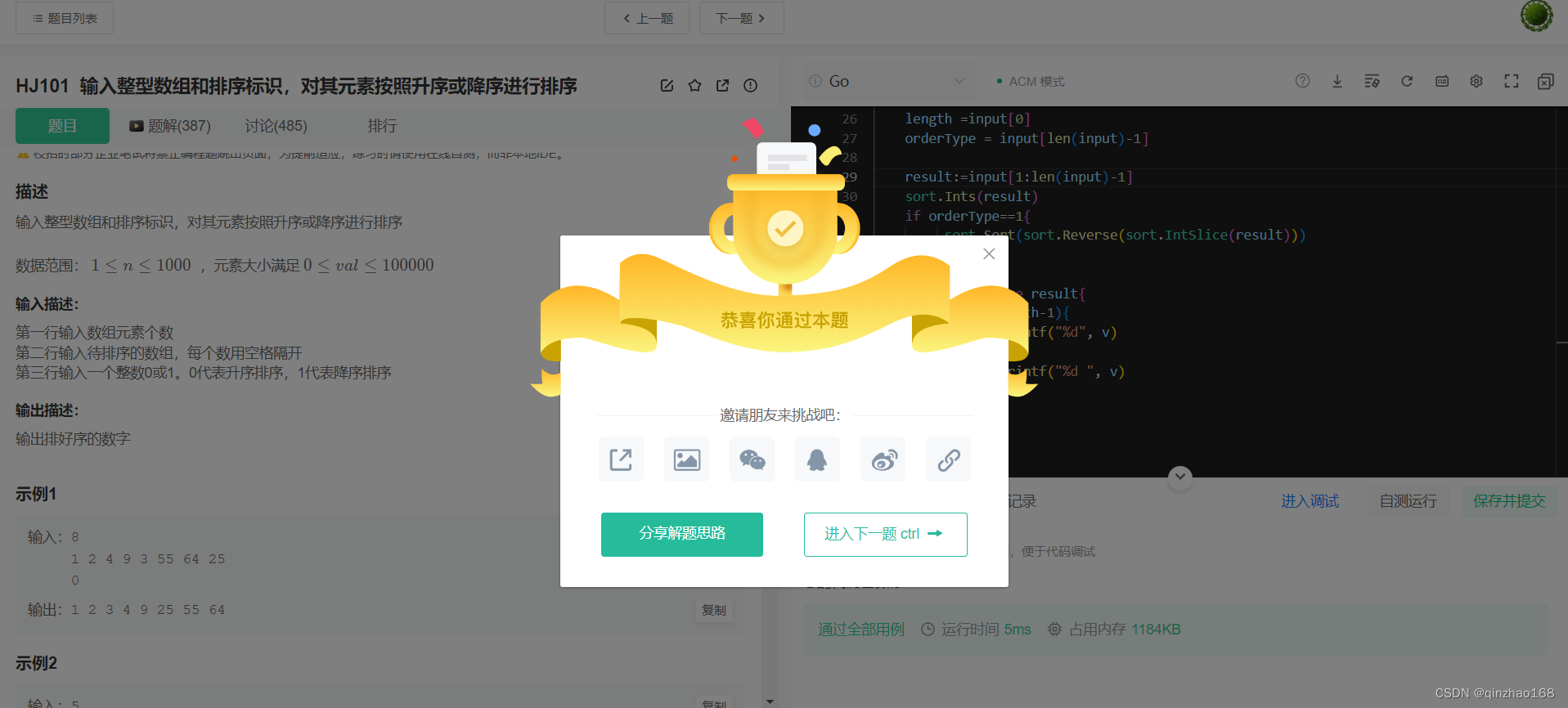
牛客 算法题 golang语言实现
题目 HJ101 输入整型数组和排序标识,对其元素按照升序或降序进行排序 描述 输入整型数组和排序标识,对其元素按照升序或降序进行排序数据范围: 1 ≤ � ≤ 10001≤n≤1000 ,元素大小满足 0 ≤ � &#…...
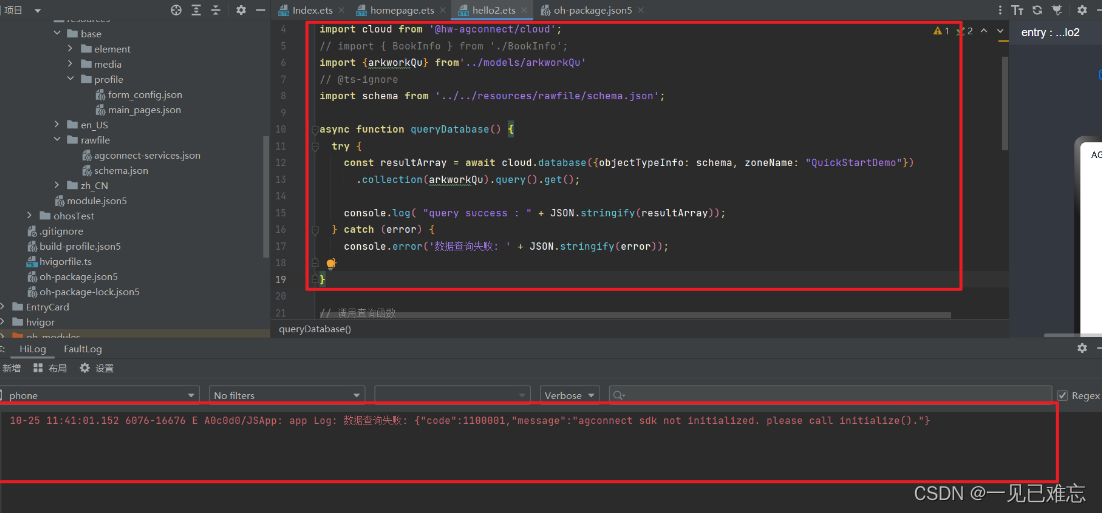
鸿蒙开发报错:agconnect sdk not initialized. please call initialize()【BUG已解决】
文章目录 项目场景:问题描述原因分析:解决方案:总结:项目场景: 鸿蒙开发报错: agconnect sdk not initialized. please call initialize() 问题描述 报错内容为: 10-25 11:41:01.152 6076-16676 E A0c0d0/JSApp: app Log: 数据查询失败: {“code”:1100001,“messag…...

极智芯 | 解读国产AI算力算能产品矩阵
欢迎关注我的公众号 [极智视界],获取我的更多经验分享 大家好,我是极智视界,本文分享一下 解读国产AI算力 华为昇腾产品矩阵。 邀您加入我的知识星球「极智视界」,星球内有超多好玩的项目实战源码和资源下载,链接:https://t.zsxq.com/0aiNxERDq 算能属于自研 TPU 阵营,…...
docker介绍、部署与常用命令
一、docker 介绍 1、容器(Container): (1) 概念: 容器是一种用于运行和部署应用程序的技术。它将应用程序及其所有依赖项(例如代码、运行时、系统工具、系统库等)打包在一个独立的、可移植的运行环境中&…...

windows定时任务命令工具schtasks
1.Schtasks概述 schtasks 是 Windows 操作系统中用于调度任务的命令行工具。它允许你在指定的时间或事件触发时运行程序或脚本。通过 schtasks 命令,你可以创建、修改、查询和删除计划任务。 2.Schtasks常用命令 查看帮助文档 schtasks /? 设定每月1号执行数据…...

多个nginx共享值、缓存问题
背景 目前我在集成登录认证功能(cas),使用的架构是nginxlua,由于我们有多个系统(全是前端项目),每套系统都采用nginxlua的方式进行部署(即每个系统都是一个nginx)&#…...

【2023传智杯】第六届传智杯程序设计挑战赛AB组-DEF题解题分析详解【JavaPythonC++解题笔记】
本文仅为【2023传智杯】第六届传智杯程序设计挑战赛-题目解题分析详解的解题个人笔记,个人解题分析记录。 本文包含:第六届传智杯程序设计挑战赛题目、解题思路分析、解题代码、解题代码详解 文章目录 一.前言更新进度记录二.比赛题目(AB俩组)D题题目-abbE题题目 -kotori和…...
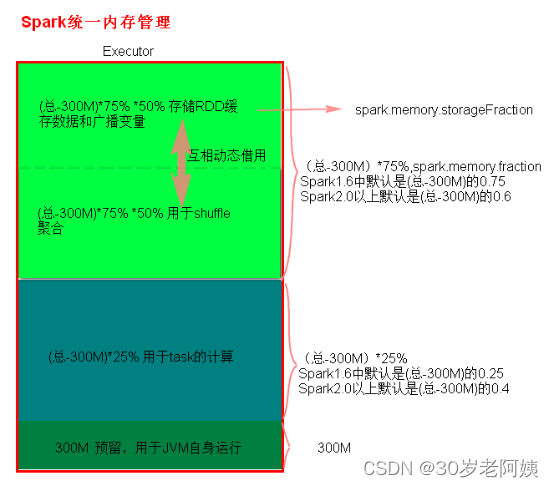
Spark---SparkCore(五)
五、Spark Shuffle文件寻址 1、Shuffle文件寻址 1)、MapOutputTracker MapOutputTracker是Spark架构中的一个模块,是一个主从架构。管理磁盘小文件的地址。 MapOutputTrackerMaster是主对象,存在于Driver中。MapOutputTrackerWorker是从对…...
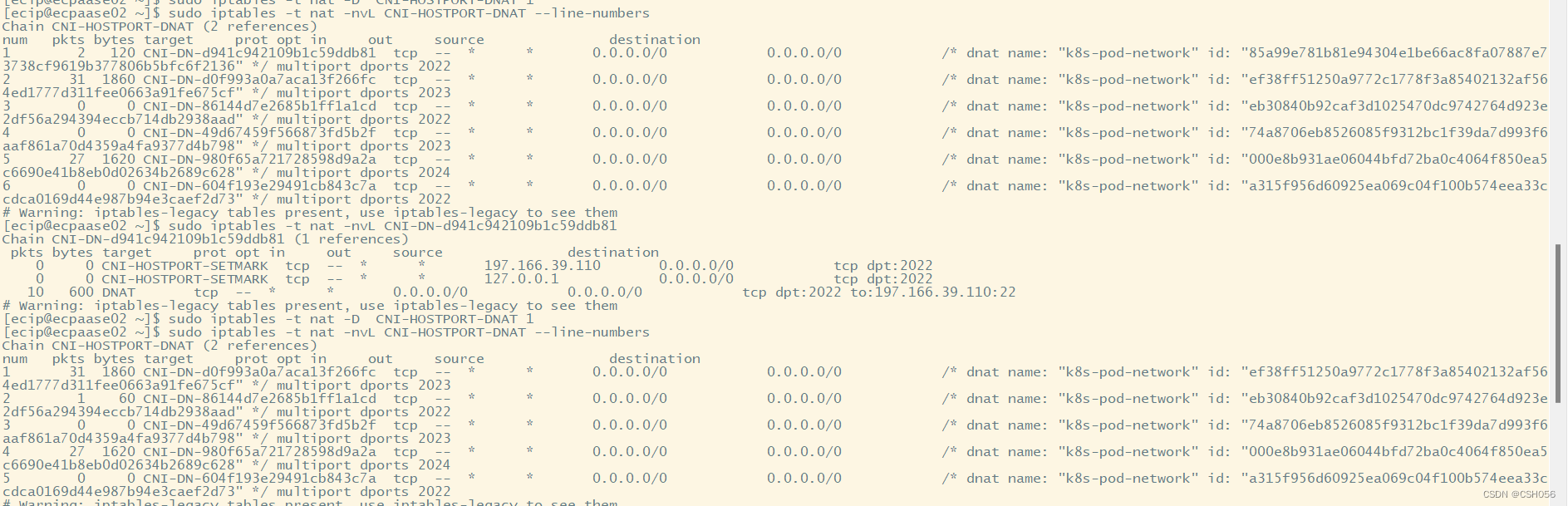
k8s中pod的hostport端口突然无法访问故障处理
故障背景: 租户告知生产环境的sftp突然无法访问了,登录环境查看sftp服务运行都是正常的,访问sftp的hostport端口确实不通。 故障处理过程 既然访问不通那就先给服务做个全面检查,看看哪里出了问题,看下sftp日志&#…...

高德开始“跑腿”
在这个万物皆可到家的时代,外卖已经不仅仅只送餐饮了,无论是鲜花、生活用品,亦或是其他急需品,只需要一个订单,就能够通通搞定。而随着消费者需求的增加,以即时物流为代表的新业态也顺势而起,并…...
Notion for Mac:打造您的专属多功能办公笔记软件
在如今这个信息爆炸的时代,一款高效、便捷的笔记软件对于办公人士来说已经成为必不可少的工具。Notion for Mac,作为一款多功能办公笔记软件,凭借其简洁优雅的界面、强大的功能以及无缝的云端同步,成为了众多用户的首选。 一、多…...
pip 安装软件出现 [No space left on device]
问题: /home文件下空间满了,安装软件可能会出现这个问题 解决方法: pip install --no-cache-dir 安装包名...
【算法刷题】Day8
文章目录 202. 快乐数解法: 11. 盛最多水的容器解法: 202. 快乐数 原题链接 拿到题,我们先看题干 把一个整数替换为每个位置上的数字平方和,有两种情况: 重复这个过程始终不到 1(无限死循环)结…...
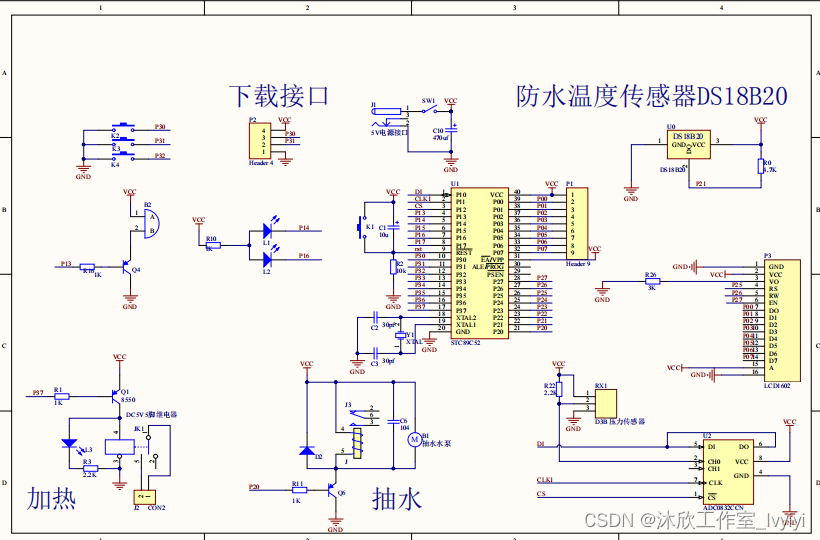
基于单片机的智能饮水机控制系统(论文+源码)
1. 系统设计 本次智能饮水机控制系统的设计研究一款以STC89C52单片机为核心的智能饮水机控制系统,其主要功能设计如下: 1.该饮水机利用DS18B20数字温度传感器实时采集饮水机内水的温度,其检测温度范围为0-100℃,精度0.1℃&#…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
