c语言-数据结构-链式二叉树
目录
1、二叉树的概念及结构
2、二叉树的遍历概念
2.1 二叉树的前序遍历
2.2 二叉树的中序遍历
2.3 二叉树的后序遍历
2.4 二叉树的层序遍历
3、创建一颗二叉树
4、递归方法实现二叉树前、中、后遍历
4.1 实现前序遍历
4.2 实现中序遍历
4.3 实现后序遍历
5、求二叉树的结点总数
6、求二叉树叶子个数
7、求第k层结点总数
8、求二叉树的高度
9、从二叉树中查找值为x的结点
10、层序遍历
11、二叉树的销毁
12、测试功能
结语:
1、二叉树的概念及结构
二叉树是由根节点和一个左子树以及一个右子树构成,且每一个结点的孩子节点可以少于两个但是不能多于两个,每个结点都带有一个数据,作为结点的有效值。二叉树示意图如下:

从上图可以看出,位于根结点左半部分的称为左子树,位于根结点右半部分的称为右子树,二叉树的顺序不能颠倒。同时2既可以看出是根结点1的孩子结点,他也可以作为3的父母结点,因此2也可以看作是一个根结点。
因此二叉树通常都采用递归的方式来实现。
2、二叉树的遍历概念
在学习数组的时候,有一个最基本的概念就是遍历数组,数组的很多问题都是在遍历数组的基础上完成的。学习链表的时候,链表的很多操作也是在遍历链表的前提下实现的。因此,要对二叉树进行一系列的操作,也需要遍历二叉树。
二叉树的遍历一般采用递归的方式,对二叉树的每个结点进行相应操作。二叉树的遍历分为:前序遍历、中序遍历、后序遍历以及层序遍历。
2.1 二叉树的前序遍历
前序遍历的顺序:根、左子树、右子树。结构图如下:
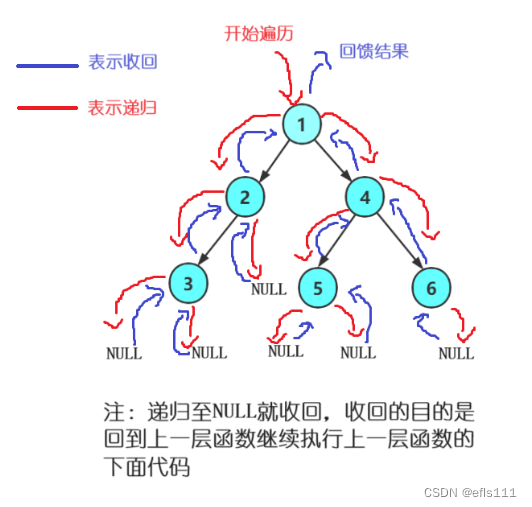
上图的二叉树前序遍历:123NNN45NN6NN(N表示NULL)。
前序遍历详解:1为根节点,因此从1开始遍历,2是1的左子树也就是遍历到2这个位置(前序遍历顺序:根-左子树-右子树),这时候会把2看成一棵树(2为根结点),然后逻辑又回到了根-左子树-右子树,3是2的左子树,因此下一个遍历的就是3,这时候又把3看成了一棵树(3为根结点),遍历3结点的左子树也就是NULL,当遍历当NULL的时候就开始“往上收回”,这时候3的左子树收回后就去遍历右子树,而这里3的右子树也是NULL因此也发生收回,最后的结果就是3结点遍历完成,同时表示结点2的左子树遍历完成,接下来就是遍历结点2的右子树,最后收回到根结点1(表示根结点1的左子树遍历完成)。接下来就是去遍历根结点1的右子树,遍历右子树的逻辑也是一样,把4看成根节点,继续根-左子树-右子树的逻辑。
2.2 二叉树的中序遍历
中序遍历的结构图与前序遍历的结构图相似,只是中序遍历的顺序不一样,中序遍历顺序为:左子树、根、右子树。
因此该二叉树的中序遍历的顺序为:N3N2N1N5N4N6N(N表示NULL)。
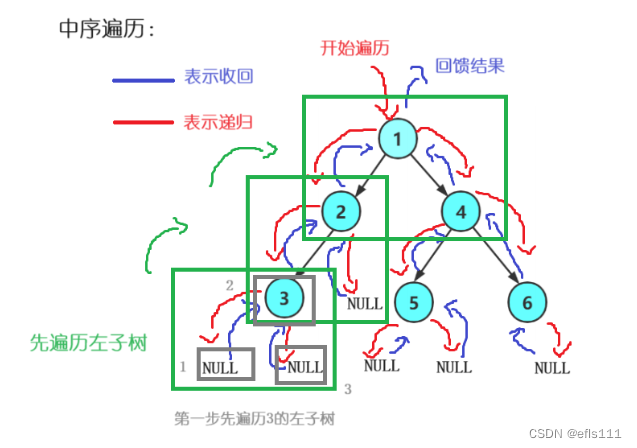
中序遍历详解:2可以看成是1的左子树,3可以看成是2的左子树,NULL是3的左子树。中序遍历的第一个是左子树,因此把3看成是一棵树并且从3入手,遍历3的左子树NULL,然后是根结点3,最后是3的右树NULL,所以顺序为N3N。接下来把3看成是2的左子树,逻辑一样为:左子树-根-右子树,3遍历完成代表2的左子树遍历完成,接下来是根结点2,然后是根结点2的右子树NULL,此时顺序为:N3N2N。2作为根结点遍历完成后,表示1的左子树遍历完成,接下来遍历的逻辑是根结点1-1的右子树,把4当成根结点执行同样的逻辑:左子树-根-右子树。
2.3 二叉树的后序遍历
接下来的后序遍历的顺序为:左子树、右子树、根。其逻辑与上述相似,只不过顺序做了调整。

该二叉树的后序遍历顺序为:NN3N2NN5NN641(N表示NULL)。
2.4 二叉树的层序遍历
层序遍历顾名思义就是一层一层、自上而下从左到右的遍历,首先从第一层也就是根结点开始,其次是第二层,并且从左边到右边的遍历,以此类推。
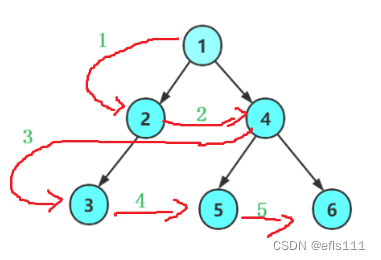
因此层序遍历的顺序为:1 2 4 3 5 6。
下面使用代码来实现二叉树及各个功能。
3、创建一颗二叉树
从二叉树的结构分析可以得出,创建二叉树要满足三个条件:有效数据、指向左孩子的指针,指向右孩子的指针。
创建二叉树代码如下:
typedef int TreeDataType;//int类型重定义
typedef struct TreeNode
{TreeDataType data;struct TreeNode* left;//指向左孩子指针struct TreeNode* right;//指向右孩子指针
}TNode;TNode* CreatTreeNode(int x)//创建结点
{TNode* treenode = (TNode*)malloc(sizeof(TNode));if (treenode == NULL){perror("CreatTreeNode");return NULL;}treenode->data = x;//给结点赋值treenode->left = NULL;treenode->right = NULL;return treenode;//返回创建树结点的地址
}TNode* CreatTree()//创造二叉树
{//创建结点TNode* n1 = CreatTreeNode(1);TNode* n2 = CreatTreeNode(2);TNode* n3 = CreatTreeNode(3);TNode* n4 = CreatTreeNode(4);TNode* n5 = CreatTreeNode(5);TNode* n6 = CreatTreeNode(6);//TNode* n7 = CreatTreeNode(7);//构建树结点之间的关系n1->left = n2;n1->right = n4;n2->left = n3;n4->left = n5;n4->right = n6;//n5->left = n7;return n1;//返回该二叉树的根节点
}该二叉树的物理图:

4、递归方法实现二叉树前、中、后遍历
4.1 实现前序遍历
前序遍历代码如下:
void PreOrder(TNode* root)//前序遍历
{if (root == NULL){printf("N ");//当递归到NULL时打印并返回Nreturn;}printf("%d ", root->data);//打印根节点PreOrder(root->left);//打印左子树PreOrder(root->right);//打印右子树
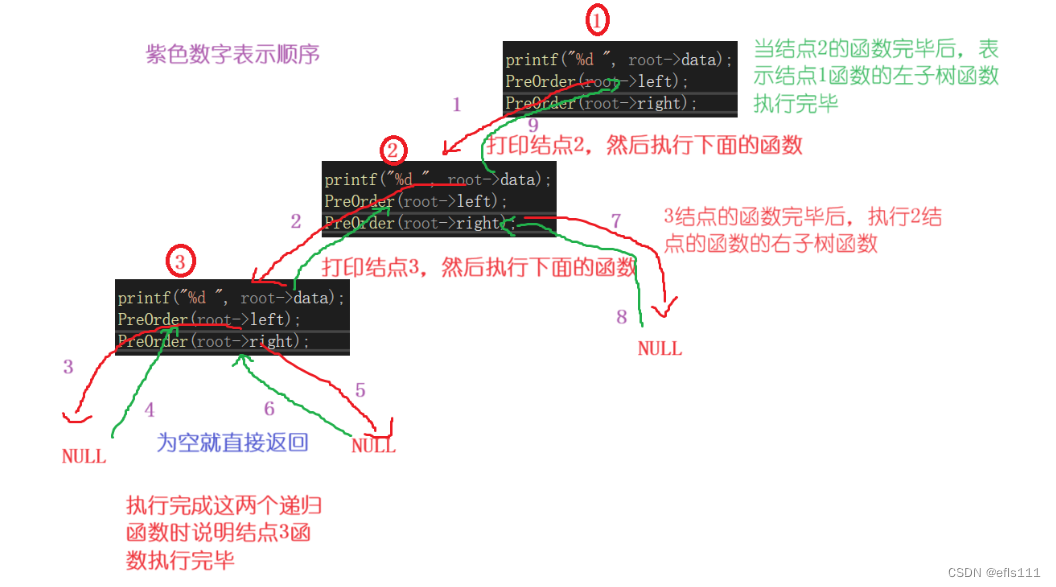
}因为二叉树是由递归实现的,并且前序遍历的顺序为:根-左子树-右子树。进入函数PreOrder时如果结点root不是空结点,则可以将该结点看成根节点,按照前序遍历的逻辑打印该结点的值,然后继续遍历该结点的左子树,和右子树,当结果为NULL时就会跳出该函数。当结点3的函数走完了,就会收回至结点2的函数,说明结点2的左子树函数完成。
具体步骤图如下:
4.2 实现中序遍历
中序遍历的顺序与前序遍历顺序不一样,因此对前序遍历的代码稍作修改即可。
中序遍历代码如下:
void InOrder(TNode* root)//中序遍历
{if (root == NULL){printf("N ");return;}//相比于前序遍历,把这两个语句的顺序交换了以下InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}可以发现,中序遍历中的打印根结点的代码与左子树代码只是做了简单的更替便可以实现中序遍历,交换后三个语句的顺序也刚好对应中序遍历的顺序:左子树-根-右子树。
4.3 实现后序遍历
经过上述的规律可以得出后序遍历的代码逻辑。
后序遍历代码如下:
void PostOrder(TNode* root)//后序遍历
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}5、求二叉树的结点总数
求二叉树结点的总数,第一步就是要遍历二叉树。因此采用的是递归的方式,因此每次函数调用返回的时候要返回当前结点的个数。
这里注意的点:当递归的函数返回一个值,是返回给上一层调用该函数的函数,如此层层返回最后返回给根结点函数。
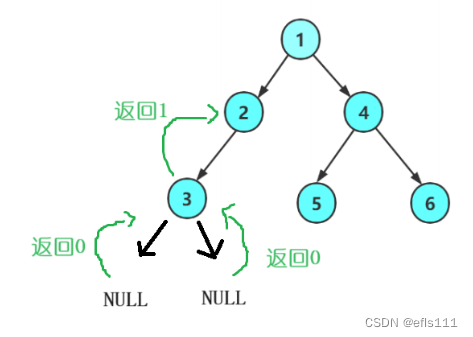
求二叉树结点总数代码如下:
int BinaryTreeSize(TNode* root)//结点个数
{if (root == NULL)//为空返回0return 0;//递归左右子树return BinaryTreeSize(root->left)+ BinaryTreeSize(root->right) + 1;//若执行到此语句说明root不为空//+1表示把当前的结点记录进去
}6、求二叉树叶子个数
把二叉树中没有孩子结点的结点称为叶子结点。
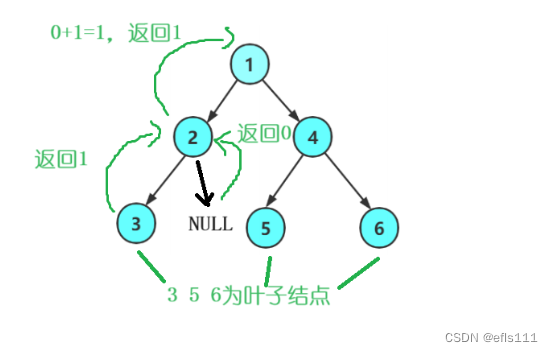
因此叶子节点的特性是其他节点不具有的,既:左孩子和右孩子都为空。因此当递归至某个结点的时候发现其左孩子和右孩子都为空,则计数+1。
求二叉树叶子个数代码如下:
int BinaryTreeLeafSize(TNode* root)//叶子个数
{if (root == NULL)//为空则不是叶子结点return 0;if (root->left == NULL && root->right == NULL)//左右孩子都为空则返回1{return 1;}elsereturn BinaryTreeLeafSize(root->left)//递归左子树+ BinaryTreeLeafSize(root->right);//递归右子树
}7、求第k层结点总数
比如求该二叉树的第三层结点总数。思路:从上往下看,如果求第三层,可以转换成求结点1的第三层,求结点2和4的第二层,求结点3 5 6 的第一层,都表示为该树的第三层,只是表达不一样。因此当k==1的时候说明这时候是在第k层。

求第k层结点总数代码如下:
int BinaryTreeLevelKSize(TNode* root, int k)//求第k层结点的总数
{if (root == NULL)return 0;if (k == 1)return 1;//递归函数,k不断-1return BinaryTreeLevelKSize(root->left, k - 1)//递归左子树+ BinaryTreeLevelKSize(root->right, k - 1);//递归右子树
}8、求二叉树的高度
思路:先遍历到最底层,然后收回的时候每一层+1,取左子树递归函数的值与右子树递归函数的值的较大值加上该层高度1就是该层的高度。示意图如下:
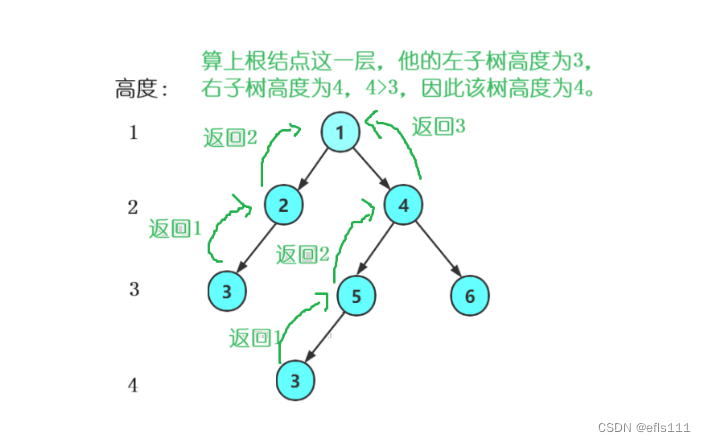
二叉树的高度代码如下:
int BinaryTreeHeight(TNode* root)//二叉树高度
{if (root == NULL)return 0;//递归函数int leftHeight = BinaryTreeHeight(root->left);//将左子树的高度存在一个变量中int rightHeight = BinaryTreeHeight(root->right);//将右子树的高度存在一个变量中//取两个变量的较大者加上该层的高度1return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}9、从二叉树中查找值为x的结点
思路:若找到该节点,则返回该节点的地址,并且用一个指针变量来接收,之后的代码就不需要再运行。
二叉树查找代码如下:
TNode* BinaryTreeFind(TNode* root, TreeDataType x)//查找值为x的结点
{if (root == NULL)//为空返回NULLreturn NULL;if (root->data == x)//若找到了则返回该结点的地址return root;TNode* xpoi= BinaryTreeFind(root->left, x);//递归左子树,找到了就存放在指针变量xpoi中if (xpoi != NULL)//如果没有找到就不执行if语句,则继续找return xpoi;xpoi= BinaryTreeFind(root->right,x);//递归右子树if (xpoi != NULL)return xpoi;return NULL;//若都没有找到则返回NULL给上层函数
}10、层序遍历
层序遍历的逻辑与前、中、后遍历的逻辑不一样,前、中、后遍历用的是递归的逻辑,而层序遍历则是采用非递归的逻辑。

层序遍历的顺序如上图:1 2 4 3 5 6,他的思路是把树节点的地址放入队列中,这样就能通过对队列节点的解引用找到树结点的地址再解引用找到树结点的值。
队列的逻辑是先进先出、后进后出, 因此先把根节点1的地址放入队列中,然后出队的时候是先出的1,同时把1的两个孩子的地址入队,此时队列中存放的是2 4,并且下一次出队先将2出掉,同时把2的孩子入队,此时队列里存放的是4 1,如此下去,最后出队的顺序为1 2 4 3 5 6,与层序遍历的顺序一样。
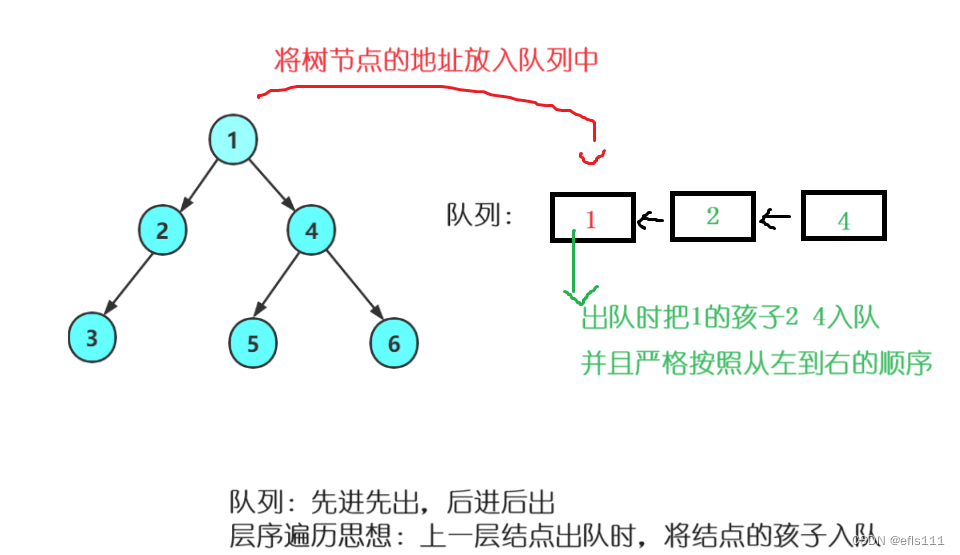
因此层序遍历的代码涉及队列的创建:
//队列结构体
typedef struct TreeNode* QueueDataType;
typedef struct QNode
{struct QNode* next;QueueDataType data;
}QNode;typedef struct Queue
{struct QNode* head;struct QNode* tail;int size;
}Queue;void QueueInit(Queue* pq)//队列初始化
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}QNode* BuyNode(QueueDataType x)//创建队列结点
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("BuyNode");return NULL;}newnode->next = NULL;newnode->data = x;return newnode;//返回队列结点的地址
}void QueuePush(Queue* pq, QueueDataType x)//入队
{assert(pq);QNode* newnode = BuyNode(x);if (pq->head == NULL){assert(pq->tail==NULL);pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}bool Empty(Queue* pq)//判空
{assert(pq);return pq->head == NULL|| pq->tail==NULL;
}QueueDataType QueueFront(Queue* pq)//显示队头数据
{assert(pq);assert(!Empty(pq));return pq->head->data;
}void QueuePop(Queue* pq)//出队
{assert(pq);assert(!Empty(pq));if (pq->head == pq->tail)//一个节点{free(pq->head);pq->head = pq->tail = NULL;}else//多个节点{QNode* poi = pq->head;pq->head = pq->head->next;free(poi);}pq->size--;}void QueueDestroy(Queue* pq)//释放队列
{assert(pq);QNode* cur = pq->head;while (cur){QNode* poi = cur->next;free(cur);cur = poi;}pq->head = pq->tail = NULL;pq->size = 0;
}//层序遍历
void LevelOrder(TNode* root)
{Queue q;QueueInit(&q);if(root!=NULL)QueuePush(&q, root);while (!Empty(&q)){TNode* front=QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if(front->left)QueuePush(&q, front->left);if(front->right)QueuePush(&q, front->right);}QueueDestroy(&q);
}11、二叉树的销毁
由于二叉树是在堆上申请而来的,因此再使用完之后要对申请的空间进行释放。这里选择用后序的方法进行释放,原因是后序的顺序是:左子树-右子树-根,根是最后才释放的,如果用前序遍历释放就会出现先把根释放了,就不好找根的左子树和右子树了,中序遍历也同理。
二叉树销毁代码如下:
void BinaryTreeDestory(TNode* root)//二叉树销毁
{if (root == NULL)return;//后序遍历BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}12、测试功能
上述解析了如此多的功能,接下来对其进行测试,观察运行结果。
测试代码如下:
int main()
{TNode* root = CreatTree();//创建树,并返回根结点PreOrder(root);//前序遍历printf("\ntreesize:%d", BinaryTreeSize(root));//树的结点个数printf("\ntreesize:%d", BinaryTreeSize(root));printf("\nLeafSize:%d", BinaryTreeLeafSize(root));//叶子个数printf("\nLevelKSize:%d", BinaryTreeLevelKSize(root, 3));//第k层结点个数printf("\nheight:%d", BinaryTreeHeight(root));//树的高度TNode* xpoi = BinaryTreeFind(root, 3);//查找结点if (xpoi == NULL)printf("二叉树无该结点\n");elseprintf("\n找到结点:%d", xpoi->data);printf("\n");LevelOrder(root);//层序遍历BinaryTreeDestory(root);//二叉树释放root = NULL;//手动置空return 0;
}运行结果:

从运行结果来看,以上功能均可正常运行。
结语:
以上就是关于二叉树以及相关功能的实现与解析,二叉树的重点在于对函数递归的形象理解,本质上二叉树就是运用函数不断递归实现的,看似一小段代码实则可以延长出很多信息。最后希望本文可以给你带来更多的收获,如果本文对你起到了帮助,希望可以动动小指头帮忙点赞👍+关注😎+收藏👌!如果有遗漏或者有误的地方欢迎大家在评论区补充~!!谢谢大家!!
(~ ̄▽ ̄)~
相关文章:

c语言-数据结构-链式二叉树
目录 1、二叉树的概念及结构 2、二叉树的遍历概念 2.1 二叉树的前序遍历 2.2 二叉树的中序遍历 2.3 二叉树的后序遍历 2.4 二叉树的层序遍历 3、创建一颗二叉树 4、递归方法实现二叉树前、中、后遍历 4.1 实现前序遍历 4.2 实现中序遍历 4.3 实现后序遍历 5、…...

DelayQueue介绍
5.1 DelayQueue介绍&应用 DelayQueue就是一个延迟队列,生产者写入一个消息,这个消息还有直接被消费的延迟时间。 需要让消息具有延迟的特性。 DelayQueue也是基于二叉堆结构实现的,甚至本事就是基于PriorityQueue实现的功能。二叉堆结构…...

centos8 redis 6.2.6源码安装+主从哨兵
文章目录 centos8 redis 6.2.6源码安装主从哨兵下载解压编译安装配置配置systemd服务启停及开机启动登录验证主从同步配置哨兵哨兵注册systemd centos8 redis 6.2.6源码安装主从哨兵 单机安装 下载解压 cd /data wget http://download.redis.io/releases/redis-6.2.6.tar.gz…...

机器学习之危险品车辆目标检测
危险品的运输涉及从离开仓库到由车辆运输到目的地的风险。监控事故、车辆运动动态以及车辆通过特定区域的频率对于监督车辆运输危险品的过程至关重要。 在线工具推荐: 三维数字孪生场景工具 - GLTF/GLB在线编辑器 - Three.js AI自动纹理化开发 - YOLO 虚幻合成数…...
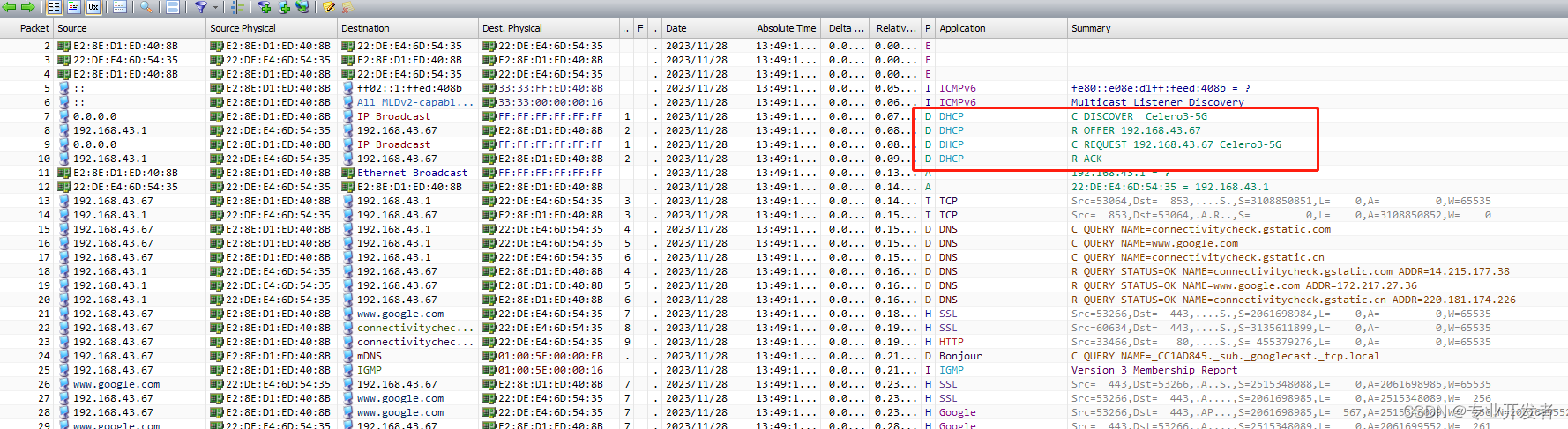
DHCP协议及实验omnipeek抓包工具分析 IPv4协议
一 抓包命令 adb shell tcpdump -i wlan0 -w /data/tcpdump.pcap 抓包后截图如下 二 DHCP是什么 2.1 DHCP定义 DHCP( Dynamic Host Configuration Protocol, 动态主机配置协议)定义: 存在于应用层(OSI) 前身是BOOTP(Bootstrap Protocol)协议 是一个使用UDP(User …...

考过了PMP,面试的时候应该怎么办?
近期喜番在后台收到了很多同学们的私信,表示自己已经过了8月份的PMP考试,开始着手往项目管理岗位转型,但是对于项目管理岗位的面试却一筹莫展。放轻松,大家的需求喜番都了解了,喜番给大家总结了一些项目经理在面试的时…...

技巧-PyTorch中num_works的作用和实验测试
简介 在 PyTorch 中,num_workers 是 DataLoader 中的一个参数,用于控制数据加载的并发线程数。它允许您在数据加载过程中使用多个线程,以提高数据加载的效率。 具体来说,num_workers 参数指定了 DataLoader 在加载数据时将创建的…...

Android:FragmentTransaction
上一篇Android:FragmentTransaction我们大概介绍了FragmentManager的大致工作流程,知道了每个动作都会添加到Op队列里,并由FragmentTransaction进行管理,那么我们就来看看FragmentTransaction的具体内容。 首先FragmentTransacti…...

5.golang字符串的拆解和拼接
字符串是 Go 中的字节切片。可以通过将一组字符括在双引号中来创建字符串" "。Go 中的字符串是兼容Unicode编码的,并且是UTF-8编码的。 访问字符串的单个字节或字符 由于字符串是字节切片,因此可以访问字符串的每个字节。 func printStr(s …...
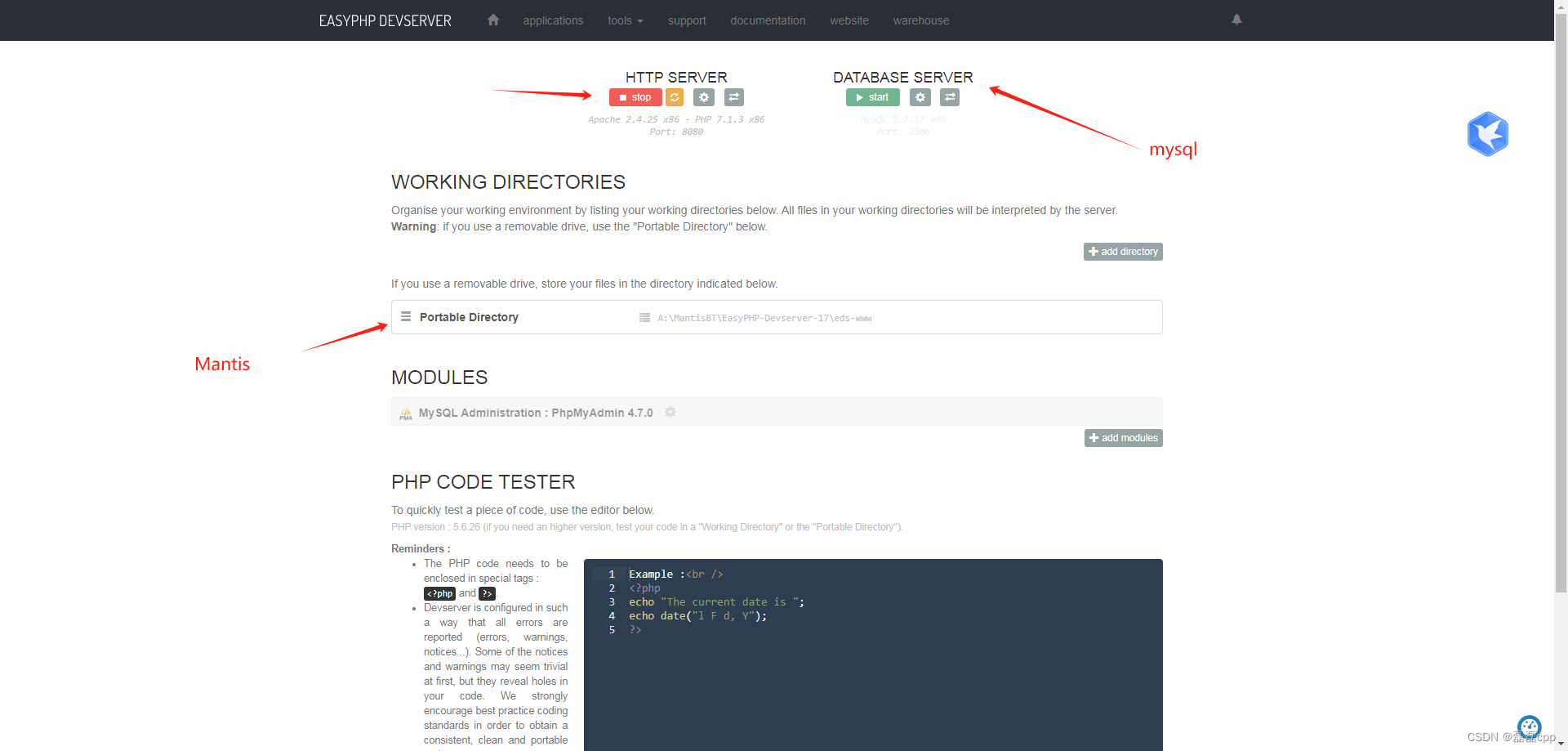
配置 Mantis 在 Windows 上的步骤
配置 Mantis Bug Tracker 在 Windows 上的步骤 Mantis Bug Tracker 是一款开源的缺陷跟踪系统,用于管理软件开发中的问题和缺陷。在 Windows 环境下配置 Mantis 可以帮助开发者更方便地进行项目管理。以下是一个详细的教程,包含了 EasyPHP Devserver 和…...

Android 单元测试初体验(二)-断言
[TOC](Android 单元测试初体验(二)-断言) 前言 当初在学校学安卓的时候,老师敢教学进度,翻到单元测试这一章节的时候提了两句,没有把单元测试当重点讲,只是说我们工作中几乎不会用到,果真在之前的几年工作当中我真的没…...
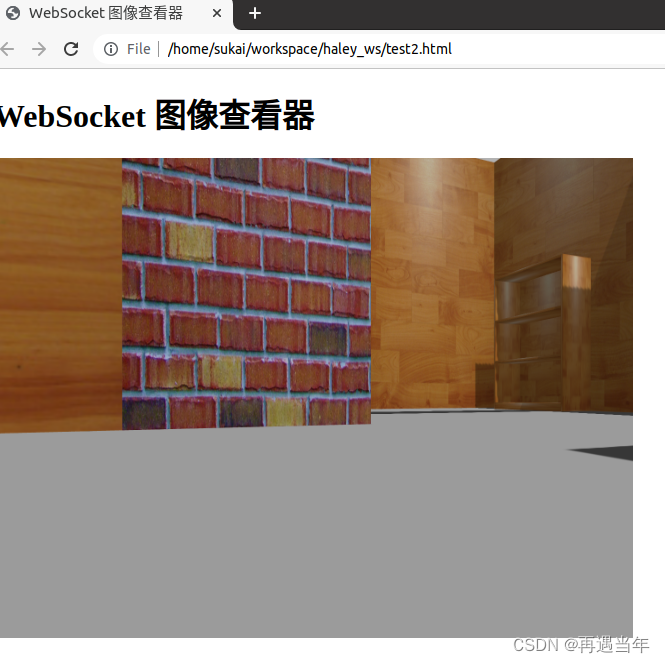
通过ros系统中websocket中发送sensor_msgs::Image数据给web端显示
通过ros系统中websocket中发送sensor_msgs::Image数据给web端显示(一) 图片数据转成base64编码方式 #include <ros/ros.h> #include <signal.h> #include <sensor_msgs/Image.h> #include <message_filters/subscriber.h> #include <message_filt…...

【 Kubernetes 风云录 】- Istio 应用多版本流量控制
文章目录 原理实现DeploymentVirtualServiceDestinationRule 约束部署 目的: 根据不同的引擎版本,可以把请求发送到指定的引擎上。可以实现版本降级。 原理 Istio通过VirtualService和DestinationRule两个资源对象来实现流量管理,其中VirtualService用于…...

比尔盖茨:GPT-5不会比GPT-4好多少,生成式AI已达到极限
比尔盖茨一句爆料,成为机器学习社区热议焦点: “GPT-5不会比GPT-4好多少。” 虽然他已不再正式参与微软的日常运营,但仍在担任顾问,并且熟悉OpenAI领导团队的想法。 消息来自德国《商报》(Handelsblatt)对…...
let const 与var的区别
1、let可以形成块级作用域,在es6之前javascript只有函数作用域,没有块级作用域。在es6之前实现块级作用域: 2、可以看到通过一个立即执行函数表达式,我们实现了一个局部作用域或者块级作用域,但是有了let之后就不需要写这样的代…...

git 把项目托管到码云
码云: 把项目托管到码云 1.注册并微活码云账号(https://gitee.com/] 2.牛成井前博 SSH公钥 (运行 ssh -t gitgitee.com 构测 SSH 公明是否有开成功) 3.创建率户的码人伦;库 4.把本地项口上传到码云对应的空白仓库中 第一:上传个新项目 cd existing_git_…...

sCrypt 现已支持各类主流前端框架
sCrypt 现已支持各类主流前端框架,包括: ReactNext.jsAngularSvelteVue 3.x or 2.x bundled with Vite or Webpack 通过在这些支持的前端框架中集成sCrypt开发环境,你可以直接在前端项目里访问合约实例和调用合约,方便用户使用Se…...
leetcode:2549. 统计桌面上的不同数字(python3解法)
难度:简单 给你一个正整数 n ,开始时,它放在桌面上。在 109 天内,每天都要执行下述步骤: 对于出现在桌面上的每个数字 x ,找出符合 1 < i < n 且满足 x % i 1 的所有数字 i 。然后,将这些…...

数据结构 / day03作业
1.顺序表按元素删除 //main.c#include "head.h" int main(int argc, const char *argv[]) {sqlist *listcreate_space();// printf("&list%p\n", list);int n;int index;data_type element, key;printf("please input n;");scanf("%d&…...

异步爬虫提速实践-在Scrapy中使用Aiohttp/Trio
在构建爬虫系统时,提高爬虫速度是一个关键问题。而使用异步爬虫技术可以显著提升爬取效率。在本文中,我将与大家分享如何在Scrapy中利用Aiohttp或Trio库实现异步爬取,以加快爬虫的速度。让我们开始吧! 1. 安装所需的库 首先&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
