LeetCode198.打家劫舍

打家劫舍和背包问题一样是一道非常经典的动态规划问题,只要做过几道动态规划的题,这道题简直就非常容易做出来。我应该花了10来分钟左右就写出来了,动态规划问题最重要的就是建立状态转移方程,就是说如何从上一个状态转移到下一个状态的。直观的说就是dp[i]是怎么来的,是通过dp[i-1]来的还是通过dp[i-2]来的等等,如果知道初始状态和状态转移方程,那么每个状态都可以算出来,以下是我的代码:
class Solution {public int rob(int[] nums) {int n = nums.length;int[][] dp = new int[n][2];dp[0][0] = 0;dp[0][1] = nums[0];int max = Math.max(dp[0][0], dp[0][1]);for(int i=1;i<n;i++){dp[i][0] = max;dp[i][1] = dp[i-1][0]+nums[i];max = Math.max(dp[i][0], dp[i][1]);}return max;}
}数组大小是n,我建立一个int[n][2]的dp数组,其中dp[i][0]表示不偷第i家能获得的最大的价值,dp[i][1]表示偷第i家能获得的最大的价值。max表是dp[i][0]和dp[i][1]中的最大值,表示偷到第i家能获得的最大价值(因为是从第0家偷到第n-1家的)。
初始状态:dp[0][0]=0; 表示不偷第0家,dp[0][1]=nums[0];表示偷第0家。
状态转移方程:dp[i][0] = max;这个max是dp[i-1]的最大值,就是说如果我不偷第i家,那么第i-1家偷不偷都可以,所以不偷第i家的最大值就是第i-1家的最大值,与偷不偷i-1无关。
dp[i][1] = dp[i-1][0]+nums[i];偷第i家的最大值就是不偷第i-1家的最大值dp[i-1][0]+第i家的价值nums[i];
最后只要返回dp[n-1][0]和dp[n-1][1]中的最大值即可,而max正好是两者中的最大值,所以只要返回max即可。
动态规划问题都是这个套路,找到状态转移方程,通过初始状态算出每个状态,返回最后那个状态或者返回所有状态中的最值。
看看题解有没有新颖的解法。
题解的思路确实更清晰,他dp数组是一维的,没有分什么偷和不偷,dp[i]就表示在第i家的最大价值也就是max,那么状态转移方程就是:dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);dp[i-2]+nums[i]表示偷第i家,那么就是在第i-2家的最大值家上nums[i];dp[i-1]就是不偷第i家,那么就是第i-1家的最大值。dp[i]取两者中的最大值即可。
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int length = nums.length;if (length == 1) {return nums[0];}int[] dp = new int[length];dp[0] = nums[0];dp[1] = Math.max(nums[0], nums[1]);for (int i = 2; i < length; i++) {dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[length - 1];}
}相关文章:

LeetCode198.打家劫舍
打家劫舍和背包问题一样是一道非常经典的动态规划问题,只要做过几道动态规划的题,这道题简直就非常容易做出来。我应该花了10来分钟左右就写出来了,动态规划问题最重要的就是建立状态转移方程,就是说如何从上一个状态转移到下一个…...
Appium PO模式UI自动化测试框架——设计与实践
1. 目的 相信做过测试的同学都听说过自动化测试,而UI自动化无论何时对测试来说都是比较吸引人的存在。相较于接口自动化来说,它可以最大程度的模拟真实用户的日常操作与特定业务场景的模拟,那么存在即合理,自动化UI测试自然也是广…...
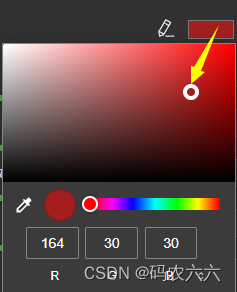
使用VUE3实现简单颜色盘,吸管组件,useEyeDropper和<input type=“color“ />的使用
1.使用vueuse中的useEyeDropper来实现滴管的功能和使用input中的type"color"属性来实现颜色盘 效果: 图标触发吸管 input触发颜色盘 组件代码部分 :<dropper> ---- vueuse使用 <template><div class"sRGBHexWrap fbc…...
)
matlab提取特征(医学图像)
乳腺肿瘤图片提取特征: %形态特征 %周长 面积 周长面积比 高度 宽度 纵横比 圆度 矩形度 伸长度 拟合椭圆长轴长 拟合椭圆短轴长 %拟合椭圆长轴与皮肤所夹锐角 最小外接凸多边形面积 最小外接凸多边形面积与肿瘤区面积比 %小叶树 叶指数 %纹理特征 %方差 熵 最小边差异 四个方…...
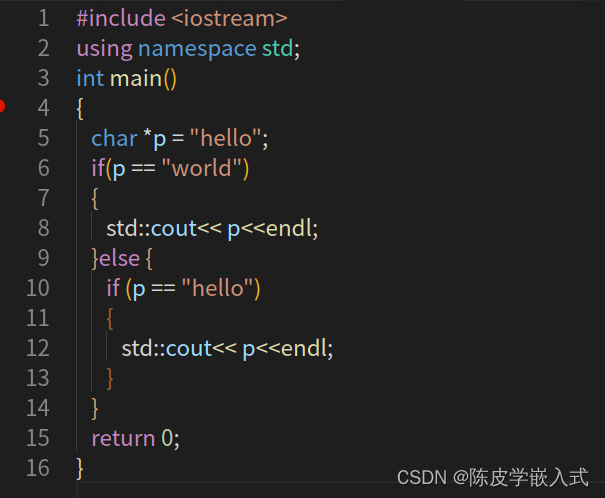
P4 C++ 条件与分支(if)
前言 今天我们来看看条件语句,换句话说,也就是 if 语句、if else 和 else if 等等这写语句。 我知道大家基本上已经非常了解 if 语句和所有 C 中的分支语句,但我还是鼓励你们继续看完这一讲,这里可能包含一些新东西。我们还会深入…...
django+drf+vue 简单系统搭建 (4) 用户权限
权限控制是web中的重要组成部分。与以往的博客系统不同,本次工具页面仅支持注册用户。 每个注册用户都能访问到工具页面,并且提交自己的task来选择具体的工具来处理自己提交的文件。每个注册用户都只能访问到自己提交的task,而管理员则可以查…...

stm32 计数模式
计数模式 但是对于通用定时器而言,计数器的计数模式不止向上计数这一种。上文基本定时器中计数器的计数模式都是向上计数的模式。 向上计数模式:计数器从0开始,向上自增,计到和自动重装寄存器的目标值相等时,计数器清…...
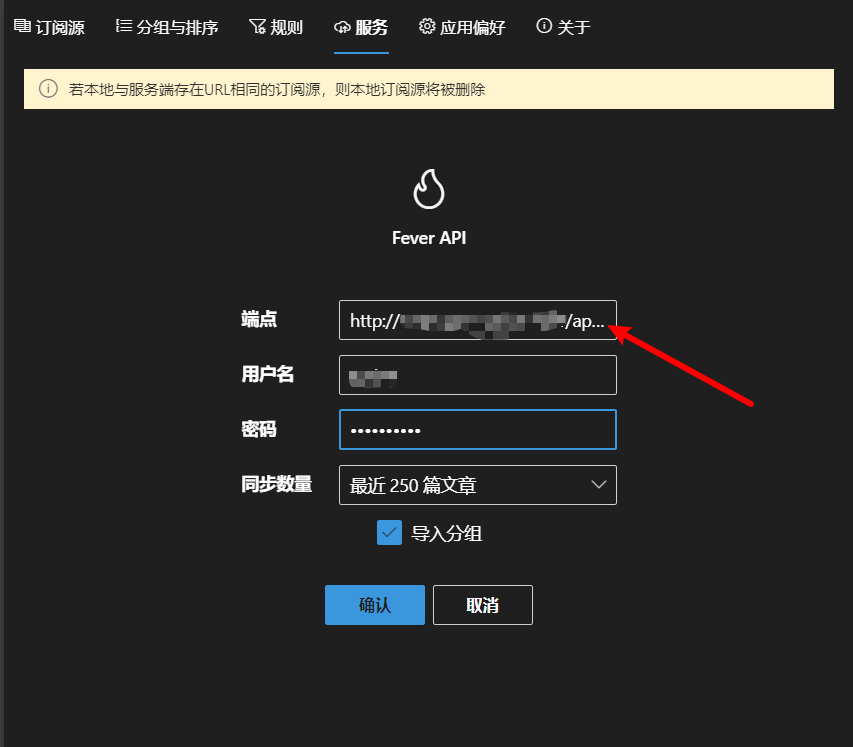
rss服务搭建记录
layout: post title: RSS subtitle: vps搭建RSS服务 date: 2023-11-27 author: Sprint#51264 header-img: img/post-bg-universe.jpg catalog: true tags: - 折腾 文章目录 引言RSShub-dockerRSS-radarFreshrssFluent reader获取fever api配置Fluent Reader同步 结语 引言 一个…...

GEE 23:基于GEE实现物种分布模型之随机森林法
基于GEE实现物种分布模型之随机森林法 1.物种分布数据2.研究区绘制3.预测因子选择 1.物种分布数据 根据研究目的和需要导入物种数据: // Load presence data var Data ee.FeatureCollection("users/************736/Distribution"); print(Original da…...
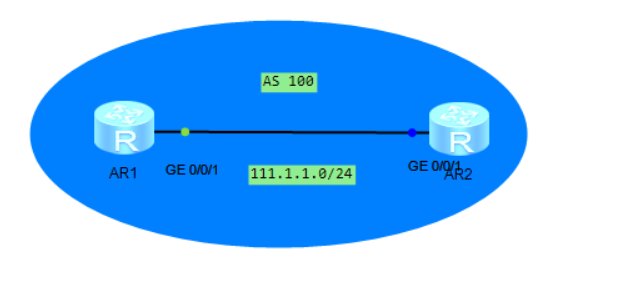
HCIE 01:基于前缀列表的BGP ORF功能
当运行BGP协议的某台设备上,针对入方向配置了基于ip-prefix的路由过滤,过滤了邻居发送的路由; 目前想,通过在peer关系的两端设备上都配置ORF功能,实现路由发送端只能送路由接收端过滤后的路由; ORF功能的说…...
基于SSM的云鑫曦科技办公自动化管理系统设计与实现
基于SSM的云鑫曦科技办公自动化管理系统设计与实现 摘 要: 随着时代的发展,单位办公方式逐渐从传统的线下纸张办公转向了使用个人pc的线上办公,办公效率低下的传统纸质化办公时代的淘汰,转型到信息化办公时代,面对当今数据逐渐膨…...

Angular项目中如何管理常量?
在Angular项目中,你可以使用不同的方式来管理常量。以下是一些常见的方法: 1、常量文件: 创建一个单独的 TypeScript 文件,其中包含你的常量。例如,创建一个名为 constants.ts 的文件,并在其中定义你的常量…...

【机器学习 | 可视化】回归可视化方案
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...

树与二叉树堆:链式二叉树的实现
目录 链式二叉树的实现: 前提须知: 前序: 中序: 后序: 链式二叉树的构建: 定义结构体: 初始化: 构建左右子树的指针指向: 前序遍历的实现: 中序…...

C++面试的一些总结day1:指针和引用的区别
文章目录 指针和引用的区别和作用定义区别作用 指针和引用的区别和作用 定义 指针:指针是一个变量,其值为指向对象的内存地址,而不是值本身。引用:可以理解为对象的别名,是另外一个变量的直接别名,用于创…...
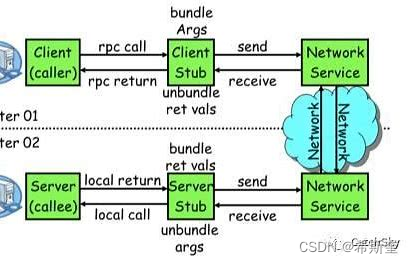
Java核心知识点整理大全15-笔记
Java核心知识点整理大全-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全2-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全3-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全4-笔记-CSDN博客 Java核心知识点整理大全5-笔记-CSDN博客 Java核心知识点整理大全6…...

初始本地仓库推送到远程仓库-git
背景(问题描述) 下面的git的操作符合的情况是: ①本地初始化一个仓库,但是还没有和远程仓库相关联; ②远程仓库也刚刚创建,里面啥也没有 然后目前就想将本地的仓库的内容和远程仓库相关联并推送到远程仓…...

OpenCV | 图像梯度sobel算子、scharr算子、lapkacian算子
import cv2 #opencv读取的格式是BGR import numpy as np import matplotlib.pyplot as plt#Matplotlib是RGB %matplotlib inline 1、sobel算子 img cv2.imread(pie.png,cv2.IMREAD_GRAYSCALE) cv2.imshow(img,img) cv2.waitKey() cv2.destroyAllWindows() pie图片 dst cv2.S…...
WS2812灯条基于WLED开源项目无门槛使用简介
WS2812灯条基于WLED开源项目无门槛使用简介 📌项目github地址:https://github.com/Aircoookie/WLED📍WLED详情地址:https://kno.wled.ge/🎈网页在线烧录固件地址:https://install.wled.me/ ✨ 仅作为使用的…...
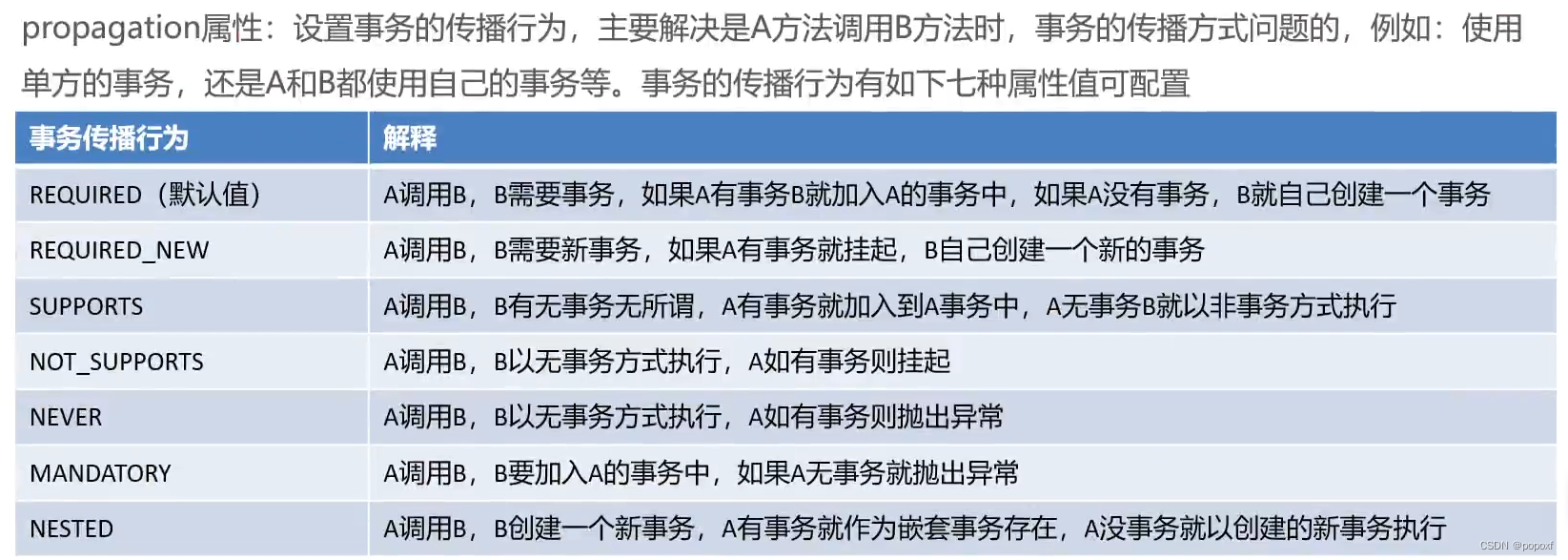
基于AOP的声明式事物控制
目录 Spring事务编程概述 基于xml声明式事务控制 事务属性 isolation timeout read-only propagation 全注解开发 Spring事务编程概述 事务是开发中必不可少的东西,使用JDBC开发时,我们使用connection对事务进行控制,使用MyBatis时&a…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

开疆智能Ethernet/IP转Modbus网关连接鸣志步进电机驱动器配置案例
在工业自动化控制系统中,常常会遇到不同品牌和通信协议的设备需要协同工作的情况。本案例中,客户现场采用了 罗克韦尔PLC,但需要控制的变频器仅支持 ModbusRTU 协议。为了实现PLC 对变频器的有效控制与监控,引入了开疆智能Etherne…...
