PyTorch学习笔记:nn.MSELoss——MSE损失
PyTorch学习笔记:nn.MSELoss——MSE损失
torch.nn.MSELoss(size_average = None,reduce = None,reduction = 'mean')
功能:创建一个平方误差(MSE)损失函数,又称为L2损失:
l(x,y)=L={l1,…,lN}T,ln=(xn−yn)2l(x,y)=L=\{l_1,\dots,l_N\}^T,l_n=(x_n-y_n)^2 l(x,y)=L={l1,…,lN}T,ln=(xn−yn)2
其中,NNN表示batch size。
函数图像:

输入:
size_average与reduce已经被弃用,具体功能可由reduction替代reduction:指定损失输出的形式,有三种选择:none|mean|sum。none:损失不做任何处理,直接输出一个数组;mean:将得到的损失求平均值再输出,会输出一个数;sum:将得到的损失求和再输出,会输出一个数
注意:
- 输入的xxx与yyy可以是任意维数的数组,但是二者形状必须一致
代码案例
对比reduction不同时,输出损失的差异
import torch.nn as nn
import torchx = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
mse_none = nn.MSELoss(reduction='none')
mse_mean = nn.MSELoss(reduction='mean')
mse_sum = nn.MSELoss(reduction='sum')
out_none = mse_none(x, y)
out_mean = mse_mean(x, y)
out_sum = mse_sum(x, y)
print(x)
print(y)
print(out_none)
print(out_mean)
print(out_sum)
输出
# 用于输入的x
tensor([0.4138, 0.1747, 0.9259, 0.2938, 0.5557, 0.9708, 0.0649, 0.6155, 0.3192, 0.1918])
# 用于输入的y
tensor([0.1024, 0.9160, 0.8386, 0.0783, 0.1479, 0.9933, 0.8791, 0.4219, 0.7586, 0.2212])
# 当reduction设置为none时,输出一个数组
# 该数组上的元素为x,y对应每个元素的平方误差损失,即对应元素做差求平方
tensor([9.6983e-02, 5.4955e-01, 7.6214e-03, 4.6433e-02, 1.6630e-01, 5.0293e-04, 6.6287e-01, 3.7512e-02, 1.9310e-01, 8.6344e-04])
# 当reduction设置为mean时,输出所有损失的平均值
tensor(0.1762)
# 当reduction设置为sum时,输出所有损失的和
tensor(1.7617)
注:绘图程序
import torch.nn as nn
import torch
import numpy as np
import matplotlib.pyplot as pltloss = nn.MSELoss(reduction='none')
x = torch.tensor([0]*100)
y = torch.from_numpy(np.linspace(-3,3,100))
loss_value = loss(x,y)
plt.plot(y, loss_value)
plt.savefig('MSELoss.jpg')
官方文档
nn.MSELoss:https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html#torch.nn.MSELoss
初步完稿于:2022年1月29日
相关文章:

PyTorch学习笔记:nn.MSELoss——MSE损失
PyTorch学习笔记:nn.MSELoss——MSE损失 torch.nn.MSELoss(size_average None,reduce None,reduction mean)功能:创建一个平方误差(MSE)损失函数,又称为L2损失: l(x,y)L{l1,…,lN}T,ln(xn−yn)2l(x,y)L…...
apache和nginx的TLS1.0和TLS1.1禁用处理方案
1、TLS1.0和TLS1.1是什么? TLS协议其实就是网络安全传输层协议,用于在两个通信应用程序之间提供保密性和数据完整性,TLS 1. 0 和TLS 1. 1 是分别是96 年和 06 年发布的老版协议。 2、为什么要禁用TLS1.0和TLS1.1传输协议 TLS1.0和TLS1.1协…...
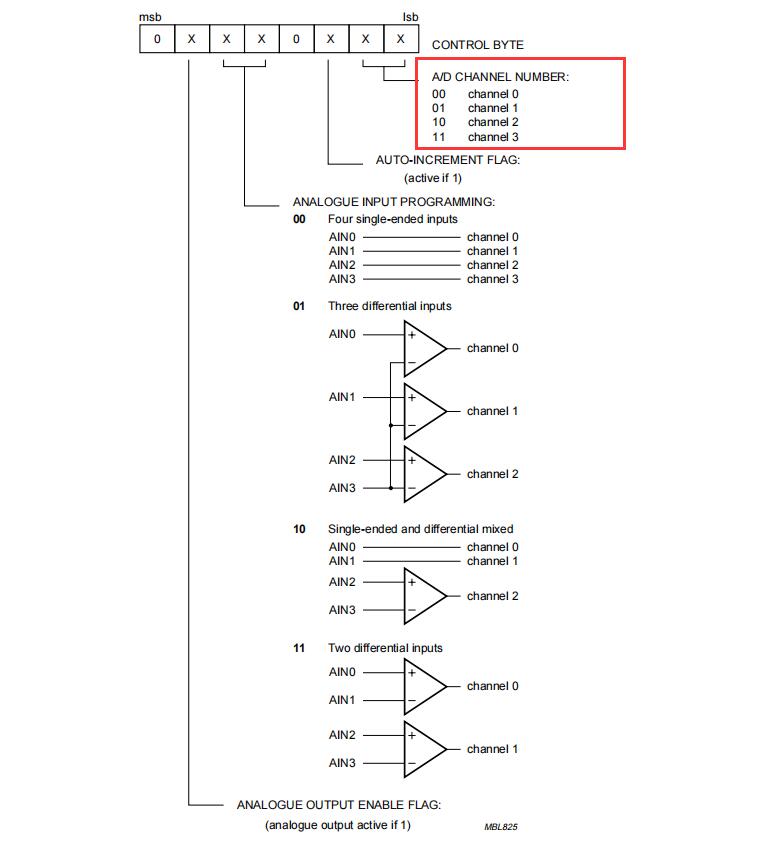
K_A12_002 基于STM32等单片机采集光敏电阻传感器参数串口与OLED0.96双显示
K_A12_002 基于STM32等单片机采集光敏电阻传感器参数串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:四、部分代码说明1、接线引脚定义1.1、STC89C52RC光敏电阻传感器模块1.2、STM32F103C8T6光敏电阻传感器模块五、基…...

《机器学习》学习笔记
第 2 章 模型评估与选择 2.1 经验误差与过拟合 精度:精度1-错误率。如果在 mmm 个样本中有 aaa 个样本分类错误,则错误率 Ea/mEa/mEa/m,精度 1−a/m1-a/m1−a/m。误差:一般我们把学习器的实际预测输出与样本的真实输出之间的差…...
前端卷算法系列(一)
前端卷算法系列(一) 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同…...

【机器学习】聚类算法(理论)
聚类算法(理论) 目录一、概论1、聚类算法的分类2、欧氏空间的引入二、K-Means算法1、算法思路2、算法总结三、DBSCAN算法1、相关概念2、算法思路3、算法总结四、实战部分一、概论 聚类分析,即聚类(Clustering)…...
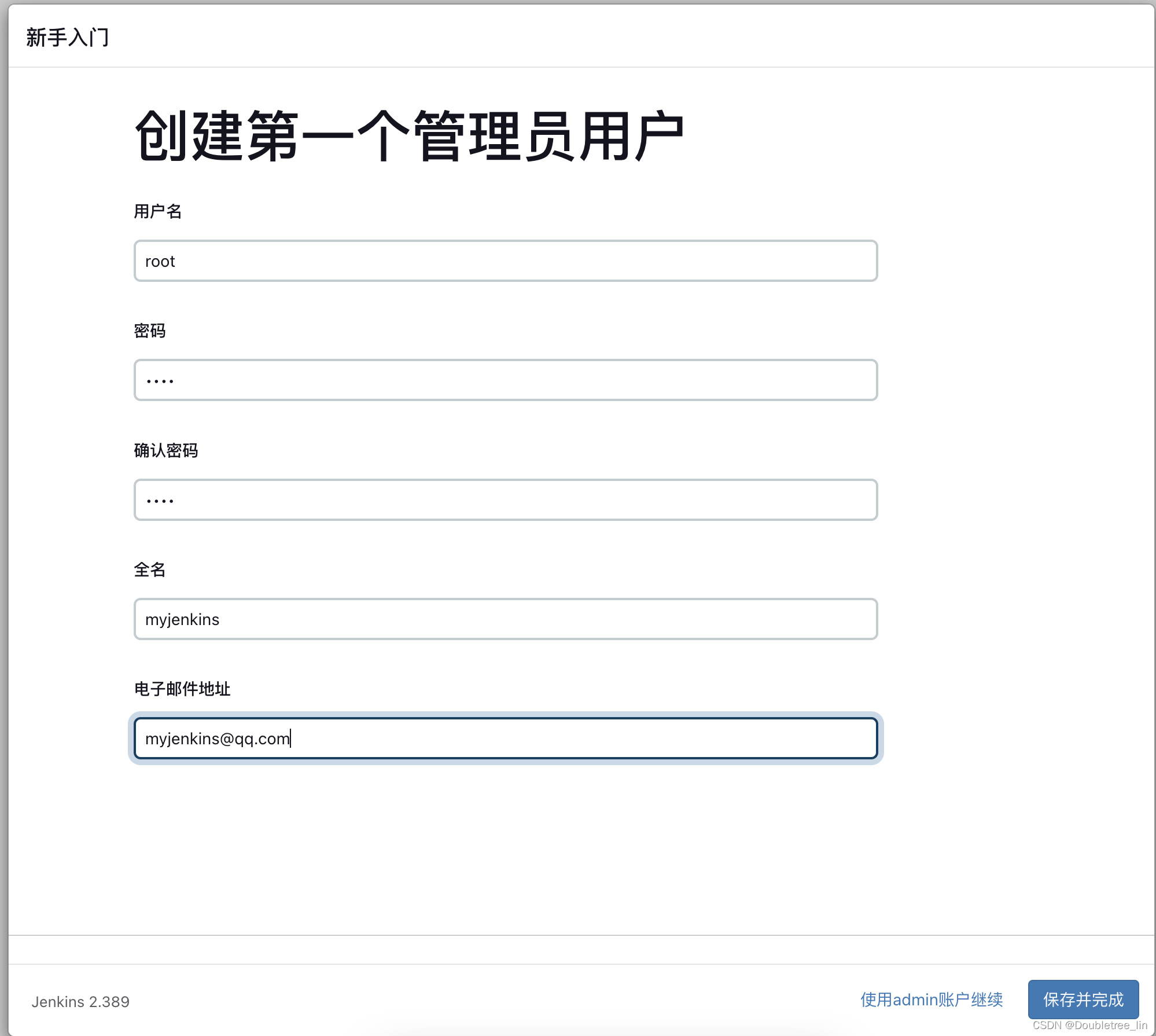
Docker-用Jenkins发版Java项目-(1)Docke安装Jenkins
文章目录前言环境背景操作流程docker安装及jenkins软件安装jenkins配置登录配置安装插件及创建账号前言 学海无涯,旅“途”漫漫,“途”中小记,如有错误,敬请指出,在此拜谢! 最近新购得了M2的MAC,…...
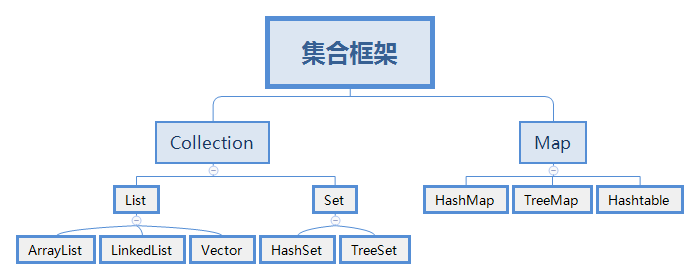
java集合框架内容整理
主要内容集合框架体系ArrayListLinkedListHashSetTreeSetLinkedHashSet内部比较器和外部比较器哈希表的原理List集合List集合的主要实现类有ArrayList和LinkedList,分别是数据结构中顺序表和链表的实现。另外还包括栈和队列的实现类:Deque和Queue。• Li…...

win10系统安装Nginx
Nginx是一款自由的、开源的、高性能的HTTP服务器和反向代理服务器,同时也提供了IMAP/POP3/SMTP服务。 Nginx可以进行反向代理、负载均衡、HTTP服务器(动静分离)、正向代理等操作。因为最近在公司使用到了Nginx 第一步:下载Nginx …...

数据库学习笔记(2)——workbench和SQL语言
1、workbench简介: 登录客户端的两种方法 在cmd中,只能通过sql语句控制数据库;workbench其实就是一种图形化数据库管理工具,在workbench中既可以通过sql语句控制数据库,也可以通过图形化界面控制数据库。通过workbenc…...

测量学期末考试之名词解释总结
仅供自己参考,且范围不全面.大地水准面与处于静止平衡状态的平均海水面重合,并延伸通过陆地的水准面高程地面点到大地水准面的铅锤距离水准面处于静止状态的水面就是水准面高差两点的水准面之间的铅锤距离垂直角在铅锤面上,瞄准目标的倾斜视线…...
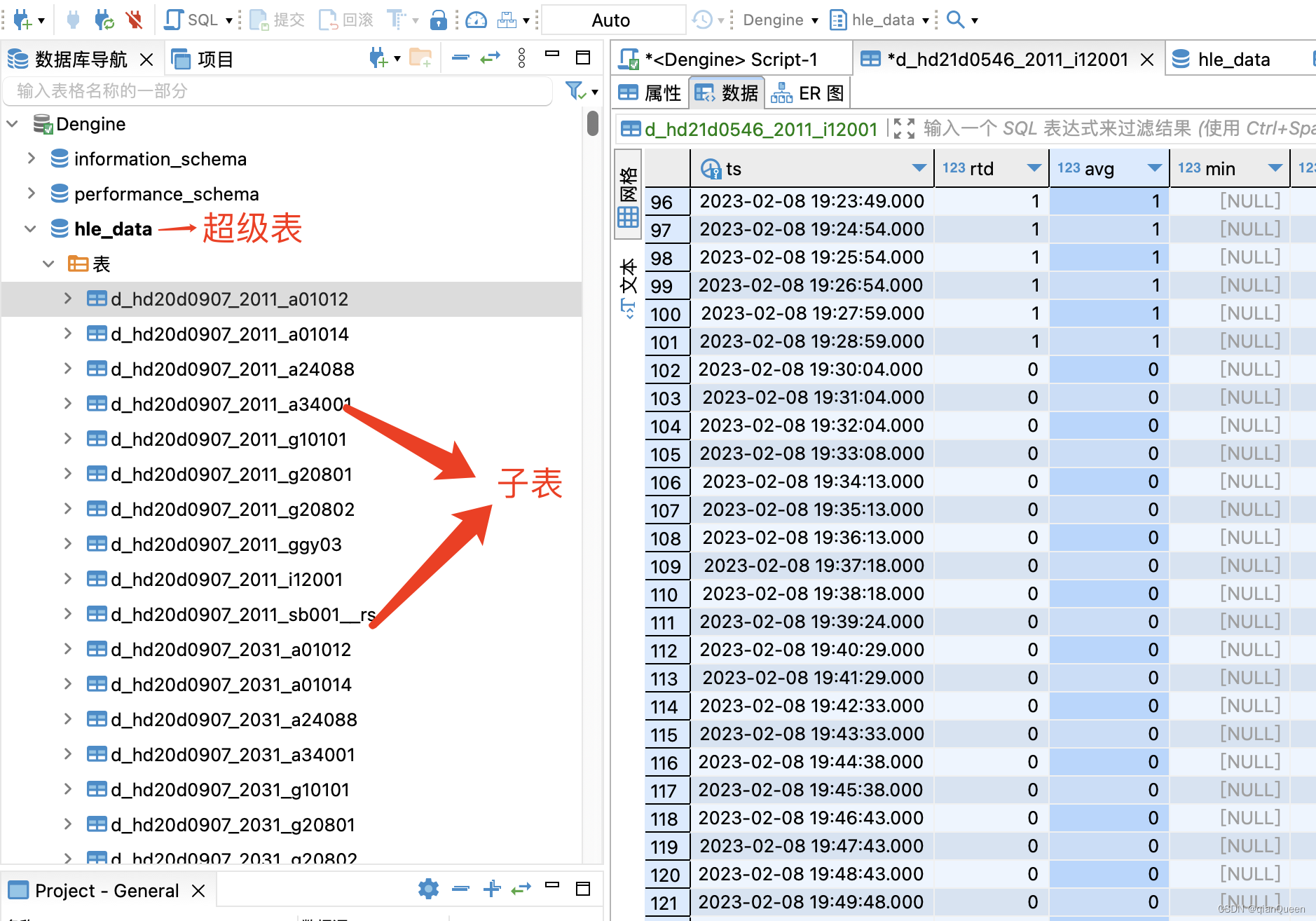
TDengine时序数据库的简单使用
最近学习了TDengine数据库,因为我们公司有硬件设备,设备按照每分钟,每十分钟,每小时上传数据,存入数据库。而这些数据会经过sql查询,统计返回展示到前端。但时间积累后现在数据达到了百万级数据,…...

记录每日LeetCode 2335.装满被子需要的最短总时长 Java实现
题目描述: 现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。 给你一个下标从 0 开始、长度为 3 的整数数组 amount ,其中 amount[0]、amount[1] 和 amount[2] 分别表示需要…...

了解线程池newFixedTheadPool
什么是线程池 操作系统 能够进行运算 调度 的最小单位。线程池是一种多线程处理形式。 为什么引入线程池的概念 解决处理短时间任务时创建和销毁线程代价较大的弊端,可以使用线程池技术。 复用 饭店只有一个服务员和饭店有10个服务员 线程池的种类 newFixedThea…...

IP分片和TCP分段解析--之IP分片
本文目录什么是IP分片为什么会产生IP分片为什么要避免IP分片如何避免IP分片什么是IP分片 IP协议栈将TCP/UDP传输层要求它发送的,但长度大于发送端口MTU的一个数据包,分割成多个IP报文后分多次发送。这些分成多次发送的多个IP报文就是IP分片。 为什么会…...

物联网方向常见通信方式有哪些?
常用的有线通信方式有串口、以太网等。 1、串口 串口通信普及率高、成本低,但是组网能力差,只适合低速率和小数据量的通信 2、以太网接口(网线) 以太网(Ethernet)是目前最普遍的一种局域网 通信技术,它规定了包括 物理层的连线、电子信号和介质访问层协议的内容。 以太…...
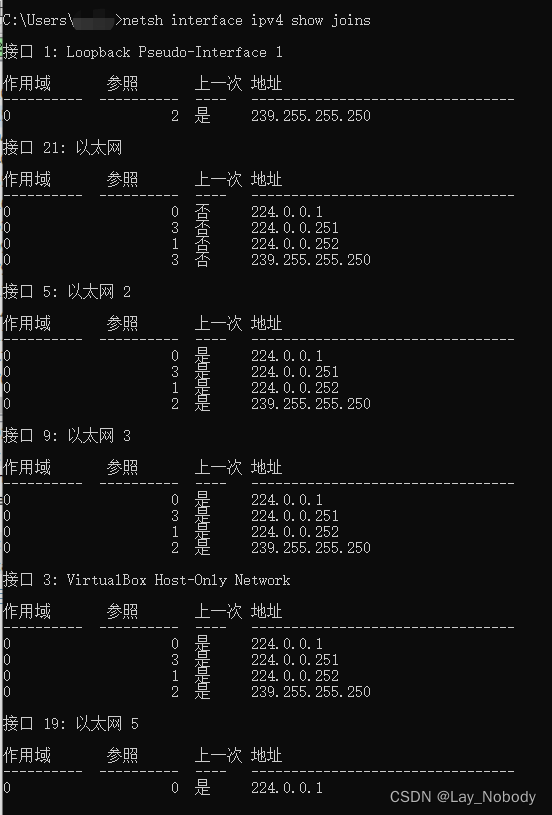
windows wireshark抓到未加入组的组播消息
现象 在Windows上开启wireshark,抓到了大量地址为239.255.255.251的组播包。 同时,根据组播相关命令,调用netsh interface ipv4 show joins,显示当前并没加入 239.255.255.251 组播组。 解决 根据IGMP Snooping,I…...
)
【PTA Advanced】1156 Sexy Primes(C++)
目录 题目 Input Specification: Output Specification: Sample Input 1: Sample Output 1: Sample Input 2: Sample Output 2: 思路 代码 题目 Sexy primes are pairs of primes of the form (p, p6), so-named since "sex" is the Latin word for "…...

项目(今日指数)
一 项目架构1.1 今日指数技术选型【1】前端技术【2】后端技术栈【3】整体概览3.2 核心业务介绍1】业务结构预览【2】业务功能简介1.定时任务调度服务XXL-JOB通过RestTemplate多线程动态拉去股票接口数据,刷入数据库; 2.国内指数服务 3.板块指数服务 4.涨…...
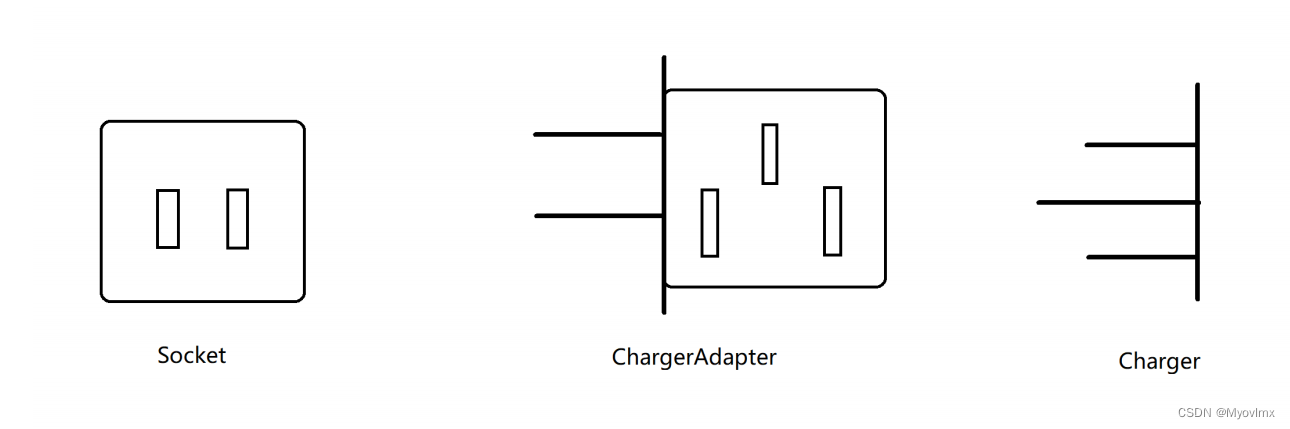
适配器模式(Adapter Pattern)
1.什么是适配器模式? 适配器模式(Adapter Pattern)是作为两个不兼容的接口之间的桥梁。这种类型的设计模式属于结构型模式,它结合了两个独立接口的功能。 这种模式涉及到一个单一的类,该类负责加入独立的或不兼容的接…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...
