【隐私计算】算术秘密分享的加法和乘法运算(Beaver Triple预处理)
在安全多方计算中(MPC)中,算术秘密分享是最基础的机制。一直有在接触,但是一直没有整理清楚最基础的加法和乘法计算流程。
算术秘密分享
概念: 一个位宽为 l l l-bit的数 x x x,被拆分为两个在 Z 2 l \mathbb{Z}_{2^l} Z2l环上的数之和。
形式化描述: 对于一个位宽为 l l l-bit的数 x x x,其算术秘密分享是 ⟨ x ⟩ A \langle x\rangle^A ⟨x⟩A,则满足 x ≡ ⟨ x ⟩ 0 A + ⟨ x ⟩ 1 A m o d 2 l x \equiv \langle x\rangle^A_0+\langle x\rangle^A_1~\mathrm{mod}~2^l x≡⟨x⟩0A+⟨x⟩1A mod 2l,其中, ⟨ x ⟩ 0 A , ⟨ x ⟩ 1 A ∈ Z 2 l \langle x\rangle^A_0, \langle x\rangle^A_1 \in \mathbb{Z}_{2^l} ⟨x⟩0A,⟨x⟩1A∈Z2l。
Share(分享)算法
P i P_i Pi生成随机数 r ∈ R Z 2 l r\in_R\mathbb{Z}_{2^l} r∈RZ2l,令 ⟨ x ⟩ i A = x − r \langle x \rangle^A_i=x-r ⟨x⟩iA=x−r作为自己的share,并将随机数 r r r发给另一方 P 1 − i P_{1-i} P1−i,即 ⟨ x ⟩ 1 − i A = r \langle x \rangle^A_{1-i}=r ⟨x⟩1−iA=r。
Reconstruct(重构)算法
P 1 − i P_{1-i} P1−i将自己的share发给 P i P_i Pi,然后 P i P_i Pi计算 x = ⟨ x ⟩ 0 A + ⟨ x ⟩ 1 A x=\langle x\rangle^A_0+\langle x\rangle^A_1 x=⟨x⟩0A+⟨x⟩1A重构真实的 x x x值。
算术秘密分享的加法
加法非常简单,两方在本地直接计算share的加法,即满足真实值的加法。
当计算 z = x + y z=x+y z=x+y时, P i P_i Pi在本地计算 ⟨ z ⟩ i A = ⟨ x ⟩ i A + ⟨ y ⟩ i A \langle z\rangle^A_i=\langle x\rangle^A_i+\langle y\rangle^A_i ⟨z⟩iA=⟨x⟩iA+⟨y⟩iA。
本地可加性很好证明, P 0 P_0 P0计算 ⟨ z ⟩ 0 A = ⟨ x ⟩ 0 A + ⟨ y ⟩ 0 A \langle z\rangle^A_0=\langle x\rangle^A_0+\langle y\rangle^A_0 ⟨z⟩0A=⟨x⟩0A+⟨y⟩0A,同时 P 1 P_1 P1计算 ⟨ z ⟩ 1 A = ⟨ x ⟩ 1 A + ⟨ y ⟩ 1 A \langle z\rangle^A_1=\langle x\rangle^A_1+\langle y\rangle^A_1 ⟨z⟩1A=⟨x⟩1A+⟨y⟩1A,于是, z = ⟨ z ⟩ 0 A + ⟨ z ⟩ 1 A = ⟨ x ⟩ 0 A + ⟨ y ⟩ 0 A + ⟨ x ⟩ 1 A + ⟨ y ⟩ 1 A = x + y z = \langle z\rangle^A_0+\langle z\rangle^A_1=\langle x\rangle^A_0+\langle y\rangle^A_0+\langle x\rangle^A_1+\langle y\rangle^A_1=x+y z=⟨z⟩0A+⟨z⟩1A=⟨x⟩0A+⟨y⟩0A+⟨x⟩1A+⟨y⟩1A=x+y,因此成立。
因此,在MPC中,秘密分享的加法只需简单的本地加法,不会引入任何通信开销。
算术秘密分享的乘法
相比于加法,乘法则复杂很多,需要依靠双方的通信来实现。
当计算 z = x ⋅ y z=x\cdot y z=x⋅y时,需要依赖预处理阶段生成的乘法三元组(Beaver Triple): c = a ⋅ b c=a\cdot b c=a⋅b,注意 a , b , c a, b, c a,b,c均与真实的输入 x , y x, y x,y无关。
下面是基于Beaver Triple计算秘密分享乘法的流程:
- P i P_i Pi本地计算 ⟨ e ⟩ i A = ⟨ x ⟩ i A − ⟨ a ⟩ i A \langle e\rangle^A_i=\langle x\rangle^A_i-\langle a\rangle^A_i ⟨e⟩iA=⟨x⟩iA−⟨a⟩iA和 ⟨ f ⟩ i A = ⟨ y ⟩ i A − ⟨ b ⟩ i A \langle f\rangle^A_i=\langle y\rangle^A_i-\langle b\rangle^A_i ⟨f⟩iA=⟨y⟩iA−⟨b⟩iA;
- 双方共同计算(重构)出 e = ⟨ e ⟩ 0 A + ⟨ e ⟩ 1 A = x − a e=\langle e\rangle^A_0+\langle e\rangle^A_1=x-a e=⟨e⟩0A+⟨e⟩1A=x−a和 f = ⟨ f ⟩ 0 A + ⟨ f ⟩ 1 A = y − b f=\langle f\rangle^A_0+\langle f\rangle^A_1=y-b f=⟨f⟩0A+⟨f⟩1A=y−b;
- P i P_i Pi本地计算 ⟨ z ⟩ i A = i ⋅ e ⋅ f + f ⋅ ⟨ a ⟩ i A + e ⋅ ⟨ b ⟩ i A + ⟨ c ⟩ i A \langle z\rangle^A_i=i\cdot e\cdot f+f\cdot \langle a\rangle^A_i+e\cdot \langle b\rangle^A_i+\langle c\rangle^A_i ⟨z⟩iA=i⋅e⋅f+f⋅⟨a⟩iA+e⋅⟨b⟩iA+⟨c⟩iA;
- 最后,重构输出 z = ⟨ z ⟩ 0 A + ⟨ z ⟩ 1 A z=\langle z\rangle^A_0+\langle z\rangle^A_1 z=⟨z⟩0A+⟨z⟩1A。
证明:
⟨ z ⟩ 0 A = f ⋅ ⟨ a ⟩ 0 A + e ⋅ ⟨ b ⟩ 0 A + ⟨ c ⟩ 0 A \langle z\rangle^A_0=f\cdot \langle a\rangle^A_0+e\cdot \langle b\rangle^A_0+\langle c\rangle^A_0 ⟨z⟩0A=f⋅⟨a⟩0A+e⋅⟨b⟩0A+⟨c⟩0A
⟨ z ⟩ 1 A = e ⋅ f + f ⋅ ⟨ a ⟩ 1 A + e ⋅ ⟨ b ⟩ 1 A + ⟨ c ⟩ 1 A \langle z\rangle^A_1=e\cdot f+f\cdot \langle a\rangle^A_1+e\cdot \langle b\rangle^A_1+\langle c\rangle^A_1 ⟨z⟩1A=e⋅f+f⋅⟨a⟩1A+e⋅⟨b⟩1A+⟨c⟩1A
z = ⟨ z ⟩ 0 A + ⟨ z ⟩ 1 A = e ⋅ f + a ⋅ f + e ⋅ b + c = ( x − a ) ( y − b ) + a ( y − b ) + ( x − a ) b + c = x y − b x − a y + a b + a y − a b + b x − a b + a b = x y z=\langle z\rangle^A_0+\langle z\rangle^A_1\\~~~=e\cdot f+a\cdot f+e\cdot b+c\\~~~=(x-a)(y-b)+a(y-b)+(x-a)b+c\\~~~=xy-bx-ay+ab+ay-ab+bx-ab+ab\\~~~=xy z=⟨z⟩0A+⟨z⟩1A =e⋅f+a⋅f+e⋅b+c =(x−a)(y−b)+a(y−b)+(x−a)b+c =xy−bx−ay+ab+ay−ab+bx−ab+ab =xy,
故成立。
Beaver Triple的生成
上面已经介绍了基于Beaver Triple计算乘法的流程,但是需要注意, c = a b c=ab c=ab也是秘密分享的形式:
c = a b = ( ⟨ a ⟩ 0 A + ⟨ a ⟩ 1 A ) ( ⟨ b ⟩ 0 A + ⟨ b ⟩ 1 A ) = ⟨ a ⟩ 0 A ⟨ b ⟩ 0 A + ⟨ a ⟩ 1 A ⟨ b ⟩ 1 A + ⟨ a ⟩ 0 A ⟨ b ⟩ 1 A + ⟨ a ⟩ 1 A ⟨ b ⟩ 0 A c=ab\\~~~=(\langle a\rangle^A_0+\langle a\rangle^A_1)(\langle b\rangle^A_0+\langle b\rangle^A_1)\\~~~=\langle a\rangle^A_0 \langle b\rangle^A_0+\langle a\rangle^A_1 \langle b\rangle^A_1+\langle a\rangle^A_0\langle b\rangle^A_1+\langle a\rangle^A_1\langle b\rangle^A_0 c=ab =(⟨a⟩0A+⟨a⟩1A)(⟨b⟩0A+⟨b⟩1A) =⟨a⟩0A⟨b⟩0A+⟨a⟩1A⟨b⟩1A+⟨a⟩0A⟨b⟩1A+⟨a⟩1A⟨b⟩0A
可以看到,第一项 ⟨ a ⟩ 0 A ⟨ b ⟩ 0 A \langle a\rangle^A_0 \langle b\rangle^A_0 ⟨a⟩0A⟨b⟩0A和第二项 ⟨ a ⟩ 1 A ⟨ b ⟩ 1 A \langle a\rangle^A_1 \langle b\rangle^A_1 ⟨a⟩1A⟨b⟩1A均可以在 P 0 , P 1 P_0, P_1 P0,P1本地计算,因此无需通信。而重点就在于后两项 ⟨ a ⟩ 0 A ⟨ b ⟩ 1 A , ⟨ a ⟩ 1 A ⟨ b ⟩ 0 A \langle a\rangle^A_0\langle b\rangle^A_1, \langle a\rangle^A_1\langle b\rangle^A_0 ⟨a⟩0A⟨b⟩1A,⟨a⟩1A⟨b⟩0A,两个share分别在两方,因此必然引入通信,通常我们将这两项称作“交叉项”或CrossTerm。
那么,Beaver Triple的生成,本质上也就是解决交叉项计算的问题。下面介绍两种常用的计算方式:
基于同态加密(HE)的Beaver Triple生成
流程如下:
- P 0 P_0 P0将 E n c ( ⟨ a ⟩ 0 A ) Enc(\langle a\rangle^A_0) Enc(⟨a⟩0A)和 E n c ( ⟨ b ⟩ 0 A ) Enc(\langle b\rangle^A_0) Enc(⟨b⟩0A)发给 P 1 P_1 P1;
- P 1 P_1 P1生成一个随机数 r r r,计算 d = E n c ( ⟨ a ⟩ 0 A ) ⟨ b ⟩ 1 A × E n c ( ⟨ b ⟩ 0 A ) ⟨ a ⟩ 1 A × E n c ( r ) d=Enc(\langle a\rangle^A_0)^{\langle b\rangle^A_1} \times Enc(\langle b\rangle^A_0)^{\langle a\rangle^A_1} \times Enc(r) d=Enc(⟨a⟩0A)⟨b⟩1A×Enc(⟨b⟩0A)⟨a⟩1A×Enc(r),然后将 d d d发给 P 0 P_0 P0;
- P 0 P_0 P0计算 ⟨ c ⟩ 0 A = ⟨ a ⟩ 0 A + ⟨ b ⟩ 0 A + D e c ( d ) = ⟨ a ⟩ 0 A ⟨ b ⟩ 0 A + ⟨ a ⟩ 0 A ⟨ b ⟩ 1 A + ⟨ a ⟩ 1 A ⟨ b ⟩ 0 A + r \langle c\rangle^A_0=\langle a\rangle^A_0+\langle b\rangle^A_0+Dec(d)=\langle a\rangle^A_0\langle b\rangle^A_0+\langle a\rangle^A_0 \langle b\rangle^A_1+\langle a\rangle^A_1 \langle b\rangle^A_0+r ⟨c⟩0A=⟨a⟩0A+⟨b⟩0A+Dec(d)=⟨a⟩0A⟨b⟩0A+⟨a⟩0A⟨b⟩1A+⟨a⟩1A⟨b⟩0A+r;
- P 1 P_1 P1计算 ⟨ c ⟩ 1 A = ⟨ a ⟩ 1 A ⟨ b ⟩ 1 A − r \langle c\rangle^A_1=\langle a\rangle^A_1\langle b\rangle^A_1-r ⟨c⟩1A=⟨a⟩1A⟨b⟩1A−r。
证明:
c = ⟨ c ⟩ 0 A + ⟨ c ⟩ 1 A = ⟨ a ⟩ 0 A ⟨ b ⟩ 0 A + ⟨ a ⟩ 1 A ⟨ b ⟩ 1 A + ⟨ a ⟩ 0 A ⟨ b ⟩ 1 A + ⟨ a ⟩ 1 A ⟨ b ⟩ 0 A = a b c=\langle c\rangle^A_0+\langle c\rangle^A_1\\~~~=\langle a\rangle^A_0 \langle b\rangle^A_0+\langle a\rangle^A_1 \langle b\rangle^A_1+\langle a\rangle^A_0\langle b\rangle^A_1+\langle a\rangle^A_1\langle b\rangle^A_0\\~~~=ab c=⟨c⟩0A+⟨c⟩1A =⟨a⟩0A⟨b⟩0A+⟨a⟩1A⟨b⟩1A+⟨a⟩0A⟨b⟩1A+⟨a⟩1A⟨b⟩0A =ab,
故成立。
如上采用的加密算法Enc是Pailler同态加密算法,其同态性如下:
- 明文加法 <=> 密文乘法;
- 明文乘法 <=> 密文指数幂
因此在上面流程的第3步中Dec(d)时才会将乘法转成加法,指数幂转成乘法。关于背后的原理参考我的另一篇博客:【密码学基础】半/全同态加密算法基础学习笔记
基于不经意传输(OT)的Beaver Triple生成
另一种常用的方式是基于COT(相关性不经意传输)的方式。
下面是计算交叉项 ⟨ a ⟩ 0 A ⟨ b ⟩ 1 A \langle a\rangle^A_0\langle b\rangle^A_1 ⟨a⟩0A⟨b⟩1A的流程:
- 在 P 0 , P 1 P_0, P_1 P0,P1之间建立COT协议通信,其中 P 0 P_0 P0作为发送方, P 1 P_1 P1作为接收方;
- 在第 i i i轮的COT通信中:
- P 1 P_1 P1输入 ⟨ b ⟩ 1 A [ i ] \langle b\rangle^A_1[i] ⟨b⟩1A[i]作为自己的选择比特, P 0 P_0 P0输入相关性函数 f Δ i ( x ) = ( ⟨ a ⟩ 0 A ⋅ 2 i − x ) m o d 2 l f_{\Delta_i}(x)=(\langle a\rangle^A_0 \cdot 2^i - x)~\mathrm{mod}~2^l fΔi(x)=(⟨a⟩0A⋅2i−x) mod 2l
- P 0 P_0 P0获得消息对 ( s i , 0 , s i , 1 ) (s_{i, 0}, s_{i, 1}) (si,0,si,1),其中, s i , 0 ∈ R Z 2 l s_{i, 0}\in _R\mathbb{Z}_{2^l} si,0∈RZ2l, s i , 1 = f Δ i ( s i , 0 ) = ( ⟨ a ⟩ 0 A ⋅ 2 i − s i , 0 ) m o d 2 l s_{i, 1}=f_{\Delta_i}(s_{i, 0})=(\langle a\rangle^A_0 \cdot 2^i - s_{i, 0})~\mathrm{mod}~2^l si,1=fΔi(si,0)=(⟨a⟩0A⋅2i−si,0) mod 2l; P 1 P_1 P1获得 s i , ⟨ b ⟩ 1 A [ i ] = ( ⟨ b ⟩ 1 A [ i ] ⋅ ⟨ a ⟩ 0 A ⋅ 2 i − s i , 0 ) m o d 2 l s_{i, \langle b\rangle^A_1[i]}=(\langle b\rangle^A_1[i]\cdot \langle a\rangle^A_0 \cdot 2^i - s_{i, 0})~\mathrm{mod}~2^l si,⟨b⟩1A[i]=(⟨b⟩1A[i]⋅⟨a⟩0A⋅2i−si,0) mod 2l;
- ⟨ u ⟩ 0 A = ( ∑ i = 0 l s i , 0 ) m o d 2 l \langle u\rangle^A_0=(\sum_{i=0}^ls_{i, 0})~\mathrm{mod}~2^l ⟨u⟩0A=(∑i=0lsi,0) mod 2l, ⟨ u ⟩ 1 A = ( ∑ i = 0 l s i , ⟨ b ⟩ 1 A [ i ] ) m o d 2 l \langle u\rangle^A_1=(\sum_{i=0}^l s_{i, \langle b\rangle^A_1[i]})~\mathrm{mod}~2^l ⟨u⟩1A=(∑i=0lsi,⟨b⟩1A[i]) mod 2l
证明:
⟨ a ⟩ 0 A ⟨ b ⟩ 1 A = ⟨ u ⟩ 0 A + ⟨ u ⟩ 1 A = ∑ i = 0 l s i , 0 + ∑ i = 0 l s i , ⟨ b ⟩ 1 A [ i ] = ∑ i = 0 l ( s i , 0 + ⟨ b ⟩ 1 A [ i ] ⋅ ⟨ a ⟩ 0 A ⋅ 2 i − s i , 0 ) = ∑ i = 0 l ( ⟨ b ⟩ 1 A [ i ] ⋅ ⟨ a ⟩ 0 A ⋅ 2 i ) \langle a\rangle^A_0 \langle b\rangle^A_1=\langle u\rangle^A_0+\langle u\rangle^A_1\\~~~~~~~~~~~~~~~~=\sum_{i=0}^ls_{i, 0}+\sum_{i=0}^l s_{i, \langle b\rangle^A_1[i]}\\~~~~~~~~~~~~~~~~=\sum_{i=0}^l(s_{i, 0}+\langle b\rangle^A_1[i]\cdot \langle a\rangle^A_0 \cdot 2^i - s_{i, 0})\\~~~~~~~~~~~~~~~~=\sum_{i=0}^l(\langle b\rangle^A_1[i]\cdot \langle a\rangle^A_0 \cdot 2^i) ⟨a⟩0A⟨b⟩1A=⟨u⟩0A+⟨u⟩1A =∑i=0lsi,0+∑i=0lsi,⟨b⟩1A[i] =∑i=0l(si,0+⟨b⟩1A[i]⋅⟨a⟩0A⋅2i−si,0) =∑i=0l(⟨b⟩1A[i]⋅⟨a⟩0A⋅2i)
注:到这一步已经非常直观了,其实就是在二进制中做乘法,一个数的每一位去乘另一个数,然后移位(乘上对应位的2的幂次)累加(对每一位的乘法结果求和)。
举例:
假设 ⟨ a ⟩ 0 A = 3 , ⟨ b ⟩ 1 A = 5 = ( 101 ) 2 \langle a\rangle^A_0=3, \langle b\rangle^A_1=5=(101)_2 ⟨a⟩0A=3,⟨b⟩1A=5=(101)2,于是:
⟨ a ⟩ 0 A ⟨ b ⟩ 1 A = ⟨ u ⟩ 0 A + ⟨ u ⟩ 1 A = ∑ i = 1 l ( s i , 0 + s i , ⟨ b ⟩ 1 A [ i ] ) = ∑ i = 1 l ( s i , 0 + ⟨ b ⟩ 1 A [ i ] ⋅ ⟨ a ⟩ 0 A ⋅ 2 i − s i , 0 ) = ∑ i = 1 l ( ⟨ b ⟩ 1 A [ i ] ⋅ ⟨ a ⟩ 0 A ⋅ 2 i ) = 1 ⋅ 3 ⋅ 2 0 + 0 ⋅ 3 ⋅ 2 1 + 1 ⋅ 3 ⋅ 2 2 = 3 + 0 + 12 = 15 \langle a\rangle^A_0 \langle b\rangle^A_1=\langle u\rangle^A_0+\langle u\rangle^A_1\\~~~~~~~~~~~~~~~~=\sum_{i=1}^l (s_{i, 0}+s_{i, \langle b\rangle^A_1[i]})\\~~~~~~~~~~~~~~~~=\sum_{i=1}^l (s_{i, 0}+\langle b\rangle^A_1[i]\cdot \langle a\rangle^A_0 \cdot 2^i - s_{i, 0})\\~~~~~~~~~~~~~~~~=\sum_{i=1}^l (\langle b\rangle^A_1[i]\cdot \langle a\rangle^A_0 \cdot 2^i)\\~~~~~~~~~~~~~~~~=1\cdot 3 \cdot 2^0+0 \cdot 3\cdot 2^1+1\cdot 3\cdot 2^2\\~~~~~~~~~~~~~~~~=3+0+12\\~~~~~~~~~~~~~~~~=15 ⟨a⟩0A⟨b⟩1A=⟨u⟩0A+⟨u⟩1A =∑i=1l(si,0+si,⟨b⟩1A[i]) =∑i=1l(si,0+⟨b⟩1A[i]⋅⟨a⟩0A⋅2i−si,0) =∑i=1l(⟨b⟩1A[i]⋅⟨a⟩0A⋅2i) =1⋅3⋅20+0⋅3⋅21+1⋅3⋅22 =3+0+12 =15,
故计算正确。
相关文章:
)
【隐私计算】算术秘密分享的加法和乘法运算(Beaver Triple预处理)
在安全多方计算中(MPC)中,算术秘密分享是最基础的机制。一直有在接触,但是一直没有整理清楚最基础的加法和乘法计算流程。 算术秘密分享 概念: 一个位宽为 l l l-bit的数 x x x,被拆分为两个在 Z 2 l \ma…...
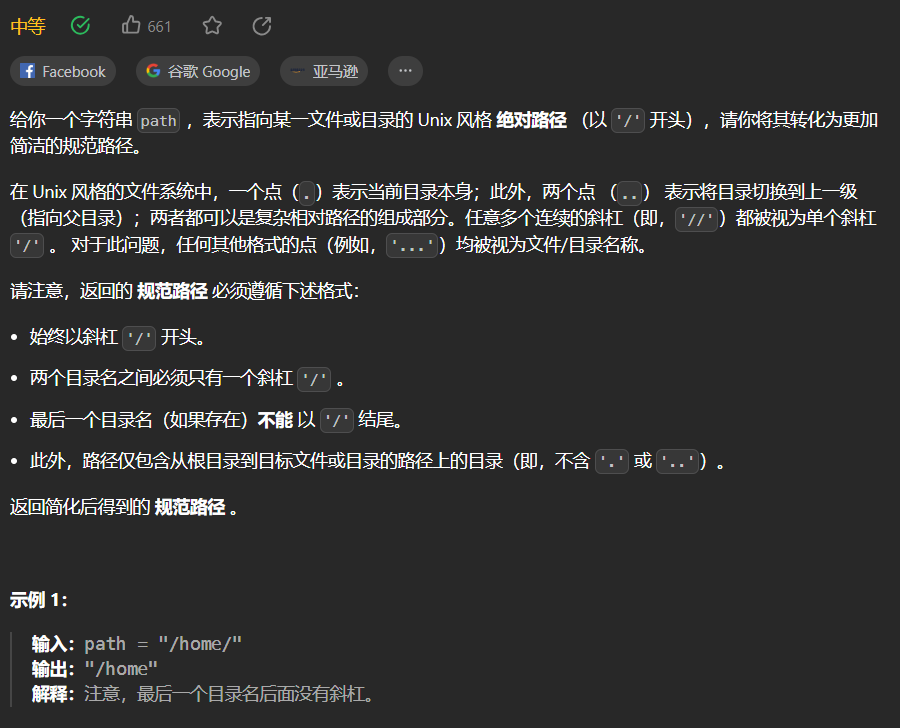
【LeetCode刷题-字符串】--71.简化路径
71.简化路径 思路: 对于给定的字符串,先根据/分割成一个由若干字符串组成的列表,记为names,根据题意names中包含的字符串只能是以下几种: 空字符串一个点两个点只包含英文字母、数字或_的目录名 对于空字符串和一个…...

数据结构与算法(Java)-树形DP题单
树形DP(灵神笔记) 543 二叉树的直径 543. 二叉树的直径 - 力扣(LeetCode) 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根…...
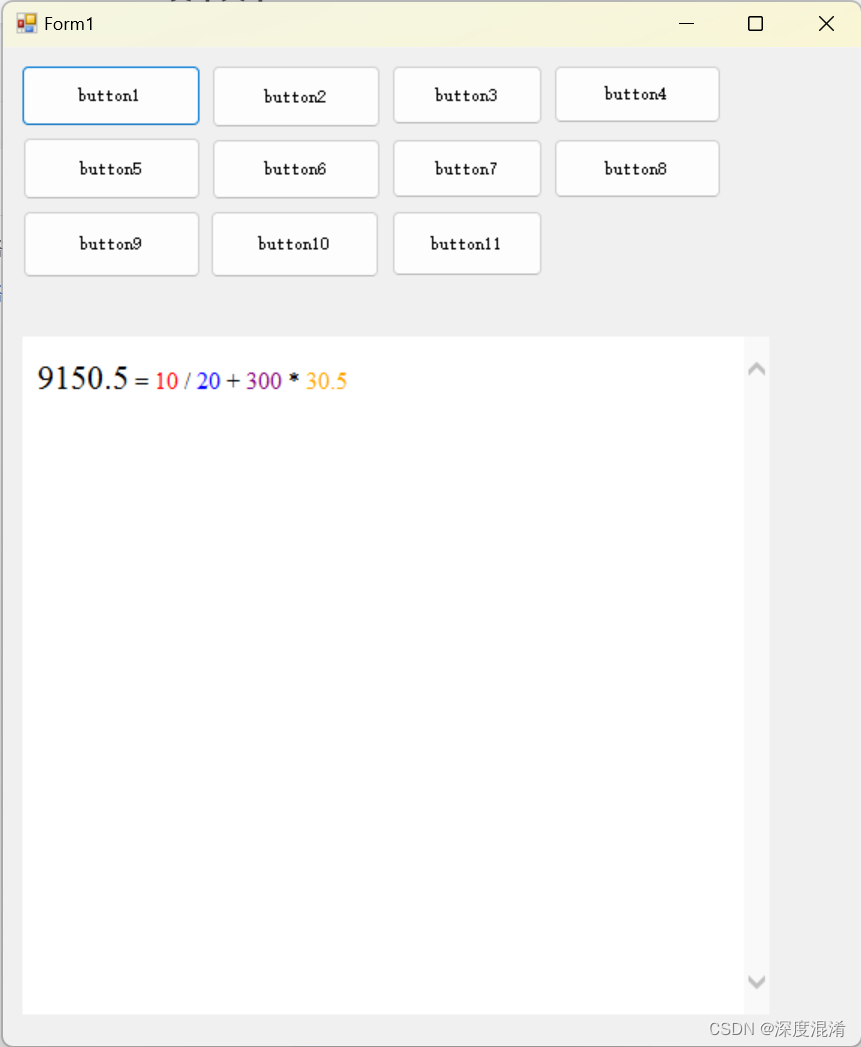
C#,《小白学程序》第一课:初识程序,变量,数据与显示
曰:扫地僧练就绝世武功的目的是为了扫地更干净。 1 引言 编程只是一项技术,如包包子,不是什么高深的科学。 学习程序最不好的方法是先学习枯燥的语法。 学习程序主要是用代码解决问题。因此,我们抛开所有的语法与诸多废物&…...

oracle的sysaux使用量排查sql
水1篇工具sql SELECT OCCUPANT_NAME,OCCUPANT_DESC,SCHEMA_NAME,MOVE_PROCEDURE,MOVE_PROCEDURE_DESC,SPACE_USAGE_KBYTES SPACE_USAGE_KB,ROUND(SPACE_USAGE_KBYTES / 1024 / 1024,2) SPACE_USAGE_GFROM V$SYSAUX_OCCUPANTS DORDER BY D.SPACE_USAGE_KBYTES DESC; 分享些经…...
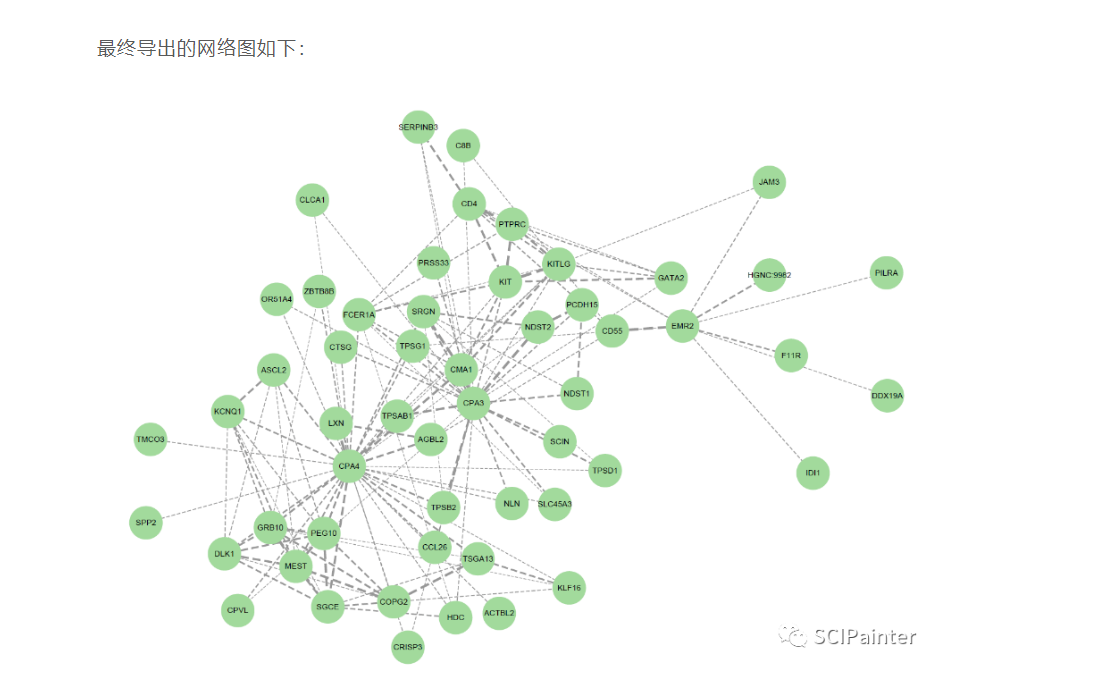
Cytoscape软件下载、安装、插件学习[基础教程]
写在前面 今天分享的内容是自己遇到问题后,咨询社群里面的同学,帮忙解决的总结。 关于Cytoscape,对于做组学或生物信息学的同学基本是陌生的,可能有的同学用这个软件作图是非常溜的,做出来的网络图也是十分的好看&am…...
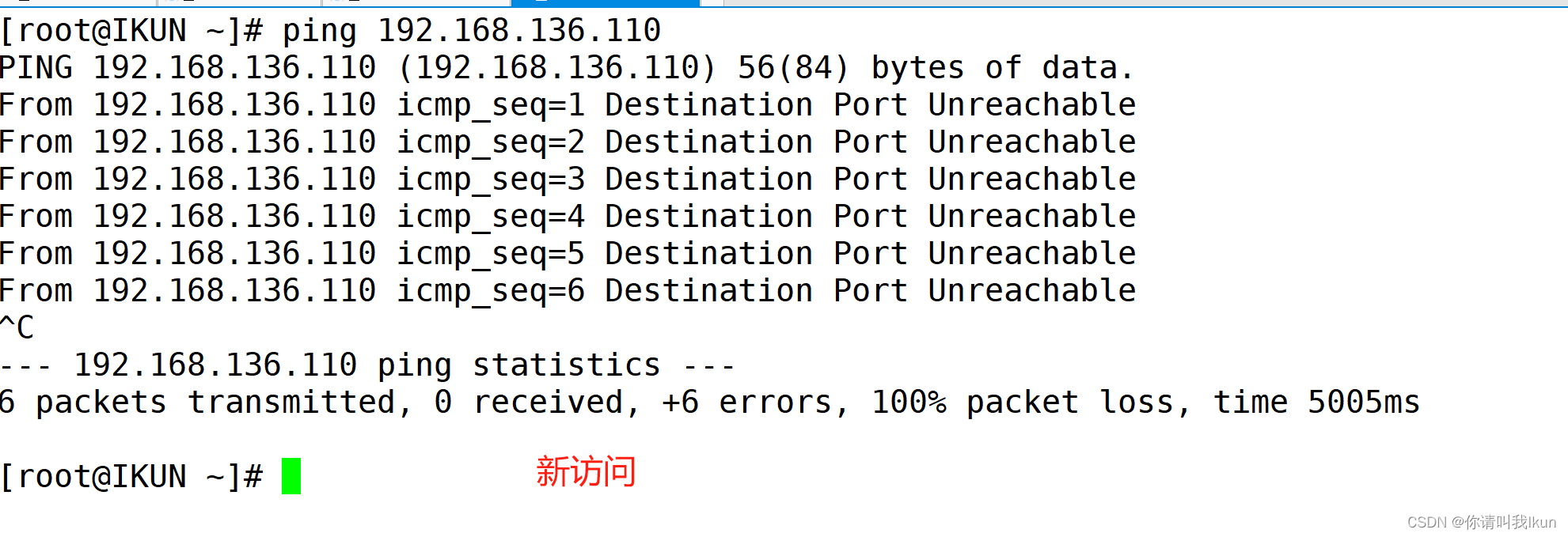
[Linux] linux防火墙
一、防火墙是什么 防火墙(FireWall):隔离功能,工作在网络或主机的边缘,数据包的匹配规则与由一组功能定义的操作组件处理的规则相匹配,根据特定规则检查网络或主机的入口和出口 当要这样做时,基…...

【开源】基于JAVA的音乐偏好度推荐系统
项目编号: S 012 ,文末获取源码。 \color{red}{项目编号:S012,文末获取源码。} 项目编号:S012,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、系统设计2.1 功能模块设计2.1.1 音乐档案模块2.1…...
架构图是什么,该怎么制作?
架构图是指可视化展示软件、系统、应用程序、网络等各种体系结构的一类图表或图形,它能够形象地展示体系结构中各个组成部分和它们之间的关系。 架构图的类型 架构图的种类比较多,逐一列举不太合适,这里只列举一些常见的架构图类型&#…...

信号类型(通信)——最小频移键控(MSK)
系列文章目录 《信号类型(通信)——仿真》 《信号类型(通信)——QAM调制信号》 《信号类型(通信)——QPSK、OQPSK、IJF_OQPSK调制信号》 目录 前言 一、MSK信号特点 1.1、最小频移 1.2、相位连续 二…...

滴滴打车崩了!全过程
滴滴发布致歉10元补偿券,文末可领取 。 事情发生于 2023年11月27日晚~28日中午,滴滴打车服务出现大面积故障,登上微博热搜。 许多用户在使用滴滴出行时遇到了无法叫车、订单异常等问题,导致大量用户滞留在外,出行受阻…...
【刷题】DFS
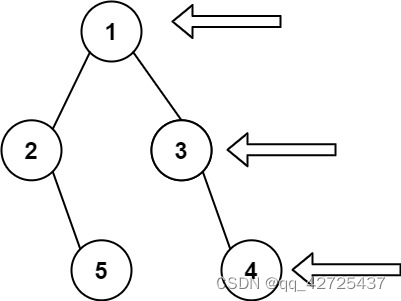
DFS 递归: 1.判断是否失败终止 2.判断是否成功终止,如果成功的,记录一个成果 3.遍历各种选择,在这部分可以进行剪枝 4.在每种情况下进行DFS,并进行回退。 199. 二叉树的右视图 给定一个二叉树的 根节点 root&#x…...

Gin投票系统(2)
投票系统 数据库的建立 先分析需求,在sql中建立数据库,关于项目数据库如何建立可以在“goweb项目创建流程分析中看如何去建表” 成功后目前有四个表: vote,user,vote_opt,vote_opt_user 建立数据库,可以…...

docker (简介、dcoker详细安装步骤、容器常用命令)一站打包- day01
一、 为什么出现 Docker是基于Go语言实现的云开源项目。 Docker的主要目标是“Build,Ship and Run Any App,Anywhere”,也就是通过对应用组件的封装、分发、部署、运行等生命周期的管理,使用户的APP(可以是一个WEB应用或数据库应…...
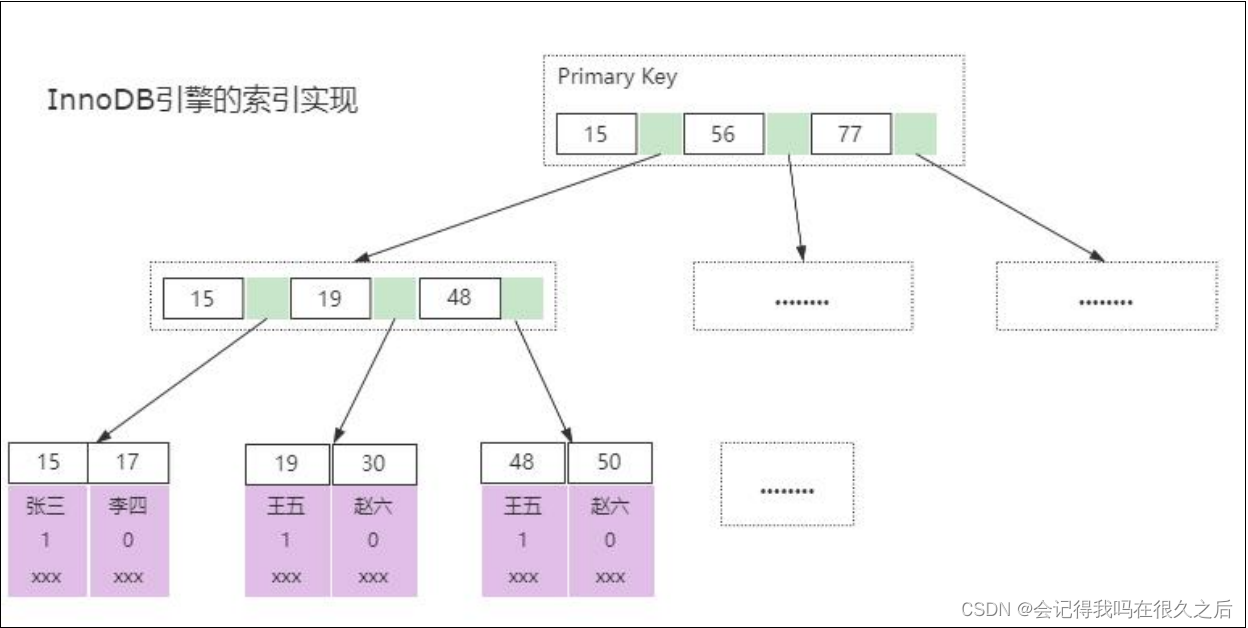
请简要说明 Mysql 中 MyISAM 和 InnoDB 引擎的区别
“请简要说明 Mysql 中 MyISAM 和 InnoDB 引擎的区别”。 屏幕前有多少同学在面试过程与遇到过类似问题, 可以在评论区留言:遇到过。 考察目的 对于 xxxx 技术的区别,在面试中是很常见的一个问题 一般情况下,面试官会通过这类…...

Nginx漏洞复现与分析
Nginx如何处理PHP请求 Nginx本身不支持直接解析和执行PHP代码,但可以通过与PHP解释器的集成来处理PHP请求。一种常见的方法是使用PHP-FPM(FastCGI Process Manager)作为PHP解释器。 原理图: Step 1 Step 2 +---------------------+ …...
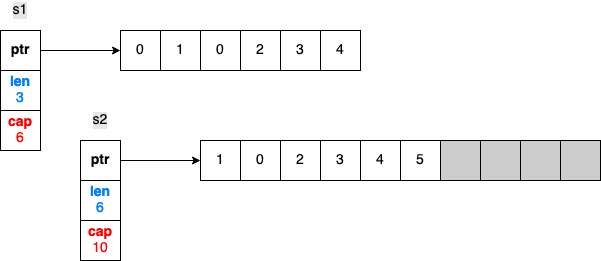
Go 中切片(Slice)的长度与容量
切片长度与容量在 Go 中很常见。切片长度是切片中可用元素的数量,而切片容量是从切片中第一个元素开始计算的底层数组中的元素数量。 Go 中的开发者经常混淆切片长度和容量,或者对它们不够了解。理解这两个概念对于高效处理切片的核心操作,比…...

顶级大厂Quora如何优化数据库性能?
Quora 的流量涉及大量阅读而非写入,一直致力于优化读和数据量而非写。 0 数据库负载的主要部分 读取数据量写入 1 优化读取 1.1 不同类型的读需要不同优化 ① 复杂查询,如连接、聚合等 在查询计数已成为问题的情况下,它们在另一个表中构…...

Java第二十章多线程
一、线程简介 线程是操作系统能够进行运算调度的最小单位,它被包含在进程之中,是进程中的实际运作单位。一个进程可以包含多个线程,这些线程可以并发执行。线程拥有自己的栈和局部变量,但是它们共享进程的其他资源,如…...

家庭教育,培养娃什么最重要?
家庭教育,培养娃什么最重要? 培养能力最重要 (我这么认为的) 时代巨变,技术变革的非常快,所以总的来说 年轻一代接触的新东西慢慢比老一代的要多,年轻一代的工作会比老一代的多而且多很多&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
