03、K-means聚类实现步骤与基于K-means聚类的图像压缩(2)
03、K-means聚类实现步骤与基于K-means聚类的图像压缩(2)
工程下载:K-means聚类实现步骤与基于K-means聚类的图像压缩
其他:
03、K-means聚类实现步骤与基于K-means聚类的图像压缩(1)
03、K-means聚类实现步骤与基于K-means聚类的图像压缩(2)
K-means聚类的图像压缩
开始学习机器学习啦,已经把吴恩达的课全部刷完了,现在开始熟悉一下复现代码。对这个手写数字实部比较感兴趣,作为入门的素材非常合适。
1、K-means聚类图像压缩基本思路
我的想法是:这副图像存在许多很大一块区域的颜色相近,既然相近,我们就用一种颜色替代一大块区域中的各色。我们可以人为的用8、16、24、32种颜色表示整幅图像的颜色,也即说明聚类的个数为8、16、24、32。
上述说法是不准确的,准确的说法是:这副图像虽然很大,但是其有些部分颜色相近,这些颜色相近的部分不论是否出自同一位置,我们都可以用一种颜色进行替代。我们可以使用8、16、24、32种颜色来代替原来图中的所有颜色。
在使用K-means聚类进行图像压缩时,聚类的对象仅仅是颜色而已,和颜色的所在位置是否相近无关,也就是说这种压缩不改变像素的大小,只改变色彩的鲜艳程度而已。具体来讲,聚类是在三维坐标下进行的,三个坐标轴分别为R G B 的具体数值。
下面简单介绍这种压缩算法的压缩效果。对于一张RGB888的彩色图像,假设其大小为1920 * 1080,那么其存储所需的大小为1920*1080 * 24(因为RGB分别用8位来表示,因此每个像素点有24位来表示其颜色)。
此处有24位来表示颜色,可表示的颜色个数为2^24种,假设此处使用K=16的K-means聚类算法对其进行压缩,则代表压缩后的图像只包含K种颜色。
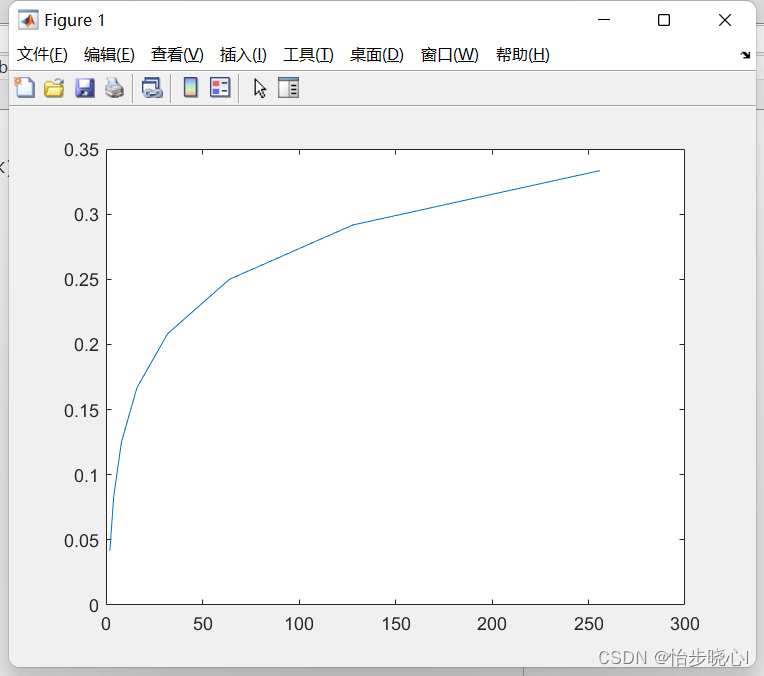
那么对于每个像素点而言,则需要log2(K)=4位来进行表示,此外还需要K*24的空间来存储对应的24位RGB颜色,因此压缩后的总空间为1920 * 1080 * log2(K)+ K * 24。
对于一张1920 * 1080 的图像,压缩比例和K的对应关系如下所示:
2、K-means聚类图像压缩底层实现
此处从K-means聚类的底层原理进行实现,不调用库函数:
import numpy as np
from matplotlib import pyplot as plt# 随机初始化聚类初始优化点
def kMeans_init_centroids(X, K):# 随机重新排序样本的索引randidx = np.random.permutation(X.shape[0])# 取前K个样本作为聚类中心centroids = X[randidx[:K]]return centroidsdef find_closest_centroids(X, centroids):# 获取聚类中心的数量,也即K值K = centroids.shape[0]# 初始化一个数组用于存储每个样本所属的聚类中心的索引idx = np.zeros(X.shape[0], dtype=int)# 遍历数据集中的每个样本for i in range(X.shape[0]):# 初始化一个列表用于存储当前样本到每个聚类中心的距离distance = []# 计算当前样本到每个聚类中心的距离for j in range(centroids.shape[0]):# 使用欧几里得距离公式计算样本i与聚类中心j之间的距离norm_ij = np.linalg.norm(X[i] - centroids[j])distance.append(norm_ij)# 找出距离列表中的最小值,该最小值对应的索引就是当前样本所属的聚类中心idx[i] = np.argmin(distance)# 返回每个样本所属的聚类中心的索引数组return idxdef compute_centroids(X, idx, K):# 获取数据集X的行数m和列数n# m表示样本数量,n表示每个样本的特征数量m, n = X.shape# 初始化一个K x n的零矩阵,用于存储K个聚类中心# K表示聚类数量,n表示特征数量centroids = np.zeros((K, n))# 遍历每个聚类中心for k in range(K):# 从数据集X中选择属于当前聚类k的所有样本# idx是一个长度为m的数组,存储了每个样本所属的聚类中心的索引points = X[idx == k]# 计算属于当前聚类k的所有样本的平均值,得到聚类中心# axis=0表示按列计算平均值centroids[k] = np.mean(points, axis=0)# 返回计算得到的K个聚类中心return centroidsdef run_kMeans(X, initial_centroids, max_iters=10):# 获取数据集X的行数m和列数n# m表示样本数量,n表示每个样本的特征数量m, n = X.shape# 获取初始聚类中心的数量KK = initial_centroids.shape[0]# 将初始聚类中心赋值给centroids变量centroids = initial_centroids# 将初始聚类中心复制给previous_centroids变量,用于后续比较聚类中心是否发生变化previous_centroids = centroids# 初始化一个长度为m的零数组,用于存储每个样本所属的聚类中心的索引idx = np.zeros(m)# 开始运行K-means算法,最多迭代max_iters次for i in range(max_iters):# 输出当前迭代进度print("K-Means iteration %d/%d" % (i, max_iters - 1))# 调用find_closest_centroids函数,为数据集X中的每个样本找到最近的聚类中心,并返回索引数组idx = find_closest_centroids(X, centroids)# 调用compute_centroids函数,根据每个样本所属的聚类中心和索引数组,计算新的聚类中心centroids = compute_centroids(X, idx, K)# 返回最终的聚类中心和每个样本所属的聚类中心的索引return centroids, idx# Load an image of a bird
original_img = plt.imread('K_means_data/bird_small.png')
# Visualizing the image
plt.imshow(original_img)
plt.show()
print("Shape of original_img is:", original_img.shape)# Divide by 255 so that all values are in the range 0 - 1
# RGB各8位,将其归一化至0-1
original_img = original_img / 255
# Reshape the image into an m x 3 matrix where m = number of pixels
# 数组的内容是图像各个点的颜色,m x 3
X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))# K就是要使用几种颜色进行表达
K = 8
max_iters = 10# Using the function you have implemented above. 初始化的是rgb的数值,因此是包含三个元素的数组
initial_centroids = kMeans_init_centroids(X_img, K)# Run K-Means - this takes a couple of minutes
centroids, idx = run_kMeans(X_img, initial_centroids, max_iters)# Represent image in terms of indices
X_recovered = centroids[idx, :]# Reshape recovered image into proper dimensions
X_recovered = np.reshape(X_recovered, original_img.shape)# Display original image
fig, ax = plt.subplots(1, 2, figsize=(8, 8))
plt.axis('off')ax[0].imshow(original_img * 255)
ax[0].set_title('Original')
ax[0].set_axis_off()# Display compressed image
ax[1].imshow(X_recovered * 255)
ax[1].set_title('Compressed with %d colours' % K)
ax[1].set_axis_off()
plt.show()3、K-means聚类图像压缩库函数实现
此处直接使用from sklearn.cluster import KMeans来进行K-means聚类,代码更加简洁了:
import matplotlib.pyplot as plt # plt 用于显示图片
import matplotlib.image as mpimg # mpimg 用于读取图片
from sklearn.cluster import KMeans
import numpy as nporiginal_pixel = mpimg.imread('K_means_data/bird_small.png')
pixel = original_pixel.reshape((128 * 128, 3))kmeans = KMeans(n_clusters=8, random_state=0).fit(pixel)newPixel = []
for i in kmeans.labels_:newPixel.append(list(kmeans.cluster_centers_[i, :]))newPixel = np.array(newPixel)
newPixel = newPixel.reshape((128, 128, 3))# Display original image
fig, ax = plt.subplots(1, 2, figsize=(8, 8))
plt.axis('off')
ax[0].imshow(original_pixel)
ax[0].set_title('Original')
ax[0].set_axis_off()# Display compressed image
ax[1].imshow(newPixel)
ax[1].set_title('Compressed with %d colours' % kmeans.n_clusters)
ax[1].set_axis_off()
plt.show()4、小结
虽说写了那么多,但是实际上还是没有输出压缩后的图片文件。压缩后的图片的大小是1920 * 1080 * log2(K)的,此外还需要K * 24位来存储颜色表,或许没办法用普通png来表示了?那应该怎么生成文件嘞?
之后一定填坑。
相关文章:

03、K-means聚类实现步骤与基于K-means聚类的图像压缩(2)
03、K-means聚类实现步骤与基于K-means聚类的图像压缩(2) 工程下载:K-means聚类实现步骤与基于K-means聚类的图像压缩 其他: 03、K-means聚类实现步骤与基于K-means聚类的图像压缩(1) 03、K-means聚类实现…...
Condition 源码解析
Condition 源码解析 文章目录 Condition 源码解析一、Condition二、Condition 源码解读2.1. lock.newCondition() 获取 Condition 对象2.2. condition.await() 阻塞过程2.3. condition.signal() 唤醒过程2.4. condition.await() 被唤醒后 三、总结 一、Condition 在并发情况下…...

acwing算法基础之数学知识--求组合数进阶版
目录 1 基础知识2 模板3 工程化 1 基础知识 请明确如下关于取余的基本定理: 数a和数b的乘积模上p,等于数a模上p和数b模上p的乘积。即, ( a ⋅ b ) m o d p ( a m o d p ) ⋅ ( b m o d p ) (a \cdot b ) \ mod \ p (a \ mod \ p) \cdot …...

基础算法:大数除以除以13
基础算法:大数除以一个数 信息学奥赛:1175:除以13 时间限制: 1000 ms 内存限制: 65536 KB 【题目描述】 输入一个大于0的大整数N,长度不超过100位,要求输出其除以13得到的商和余数。 【输入】 一个大于0的大整数&…...

软件版本区分
引言 定义好版本号对于产品的版本发布与持续更新很重要但是对于版本怎么定义规则如何确定却是千差万别。具体应用可以结合自己目前的实际情况命名。另外对于商业软件有的产品号称是永远的Beta版持续不断地更新、优化迭代产品才有生命力。 ⭕ 软件版本周期 α、β、λ 常用来…...
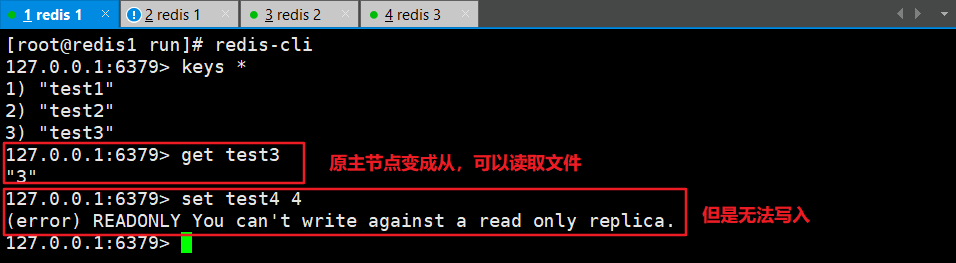
Redis高可用之主从复制及哨兵模式
一、Redis的主从复制 1.1 Redis主从复制定义 主从复制是redis实现高可用的基础,哨兵模式和集群都是在主从复制的基础之上实现高可用; 主从复制实现数据的多级备份,以及读写分离(主服务器负责写,从服务器只能读) 1.2 主从复制流…...
代理模式,dk动态代理,cglib动态代理
目录 一、代理模式1、生活中代理案例2、为什么要使用代理3、代理模式在Java中的应用4、什么是代理模式 二、代理的实现方式1、java中代理图示2、静态代理 三、动态代理1、概述2、JDK动态代理jdk动态代理原理分析 3、Cglib动态代理3.1 基本使用3.2 cglib基本原理 一、代理模式 …...
Vue2系列 -- 组件自动化全局注册(require.context)
参考官网:https://v2.cn.vuejs.org/v2/guide/components-registration.html 1 作用 省略 import 引入组件 省略 在main.js 中注册 实现自动化引入组件 2 自定义文件夹 在 src 下新建一个 components/base 文件夹,用于存放要自动注册的组件 3 在 base…...

【华为OD题库-038】支持优先级的对列-java
题目 实现一个支持优先级的队列,高优先级先出队列,同优先级时先进先出。 如果两个输入数据和优先级都相同,则后一个数据不入队列被丢弃。 队列存储的数据内容是一个 整数。 输入描述 一组待存入队列的数据(包含内容和优先级)。 输出描述 队列…...

python爱心代码高级
在Python中,我们可以使用matplotlib库来创建一个更高级的爱心图形。以下是一个示例: import matplotlib.pyplot as pltimport numpy as npx np.linspace(-2, 2, 1000)y1 np.sqrt(1-(abs(x)-1)**2)y2 -3*np.sqrt(1-(abs(x)/2)**0.5)fig, ax plt.subp…...
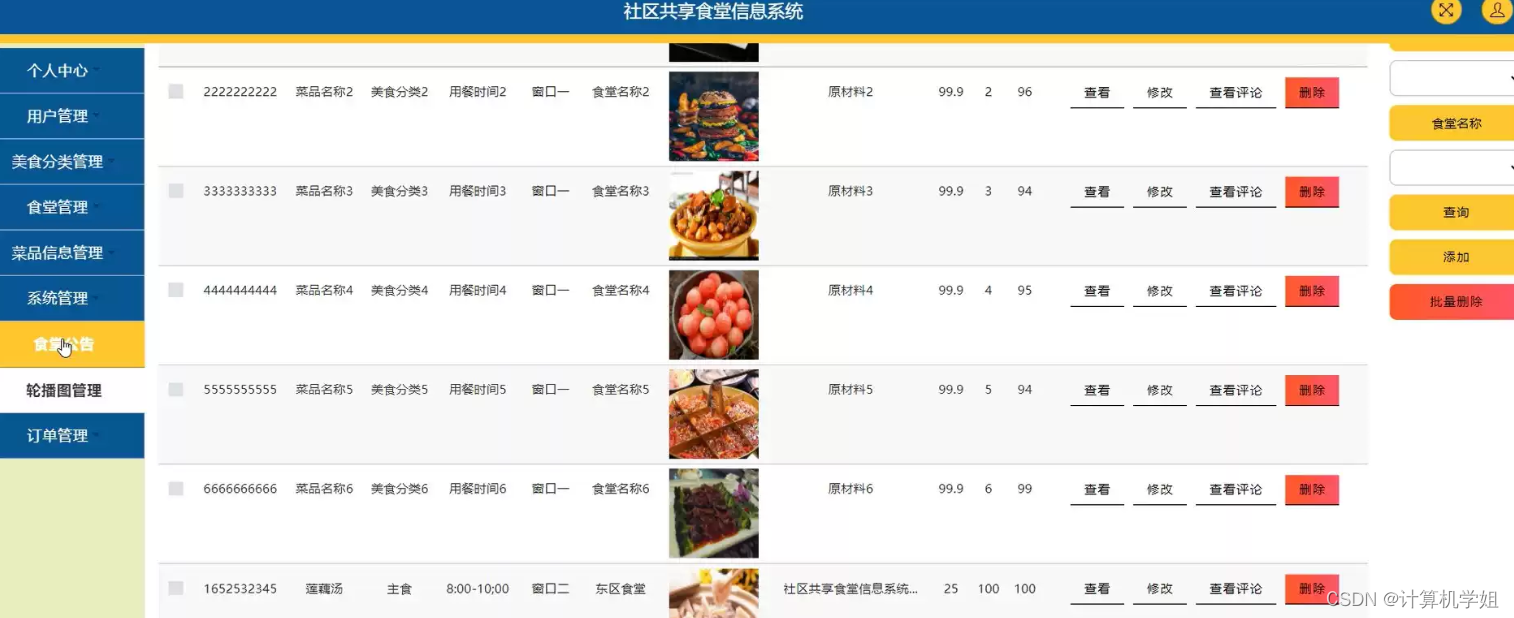
基于SSM+Vue的社区共享食堂管理系统
基于SSM的社区共享食堂管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringMyBatisSpringMVC工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 菜品详情 管理员界面 摘要 社区共享食堂管理系统是一种基于SSM…...

MYSQL基础知识之【修改数据,删除数据】
文章目录 前言MySQL UPDATE 查询使用PHP脚本更新数据 MySQL DELETE 语句从命令行中删除数据使用 PHP 脚本删除数据 后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:Mysql 🐱👓博主在前端领域还有很多知识和技术…...

【机器学习】交叉验证 Cross-validation
交叉验证(CrossValidation)方法思想简介 以下简称交叉验证(Cross Validation)为CV.CV是用来验证分类器的性能一种统计分析方法,基本思想是把在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set),首先用训练集对分类器进…...
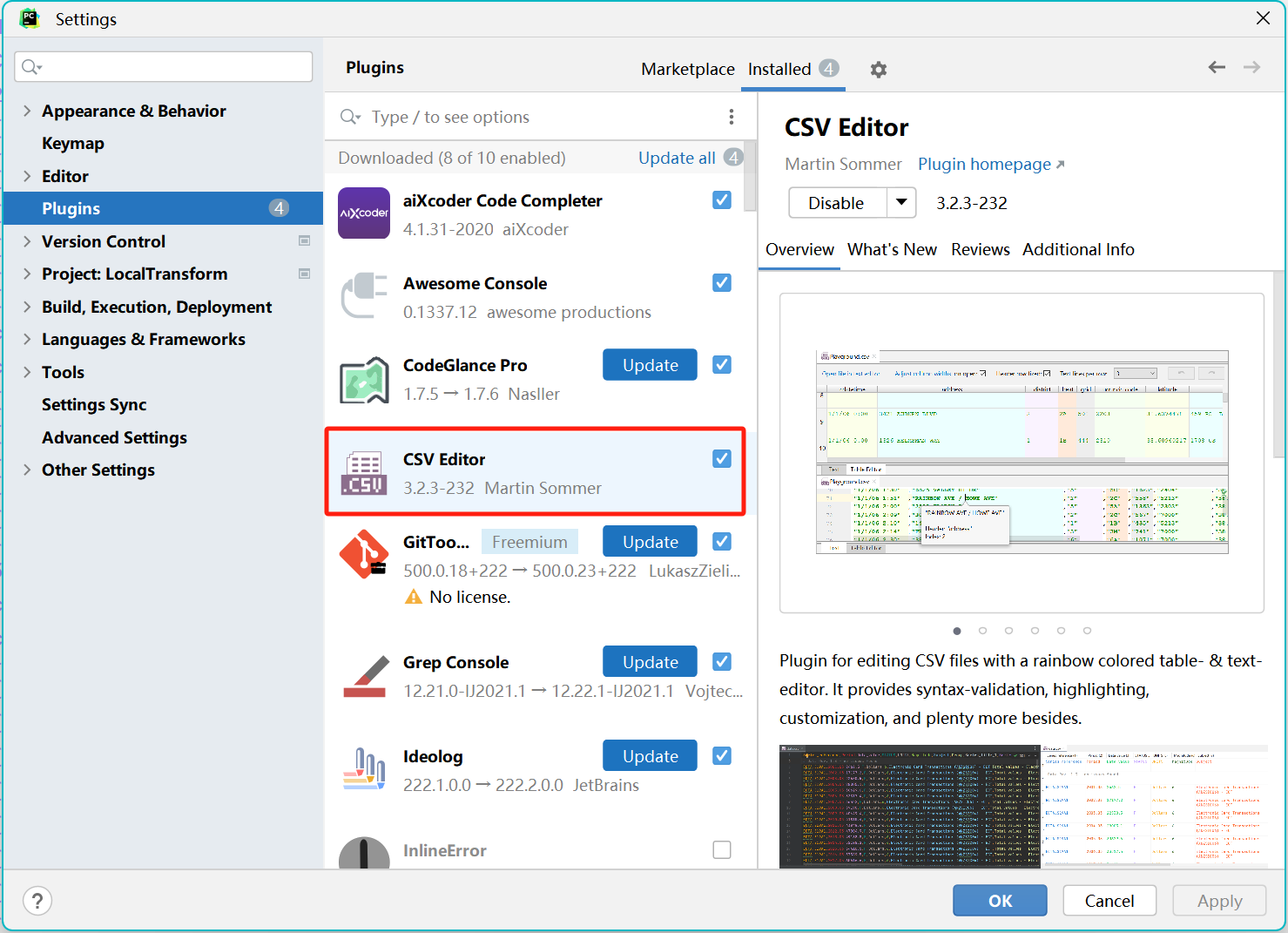
Pycharm修改文件默认打开方式 + CSV Editor插件使用
1、File —> Settings —> Editor —> File Types 然后将*csv添加到最上面 在plugins中下载插件,CSV Editor 备注:不在上一步的“File Types”中将*.csv设置为CSV格式,插件是不起作用的 就可以使用了...
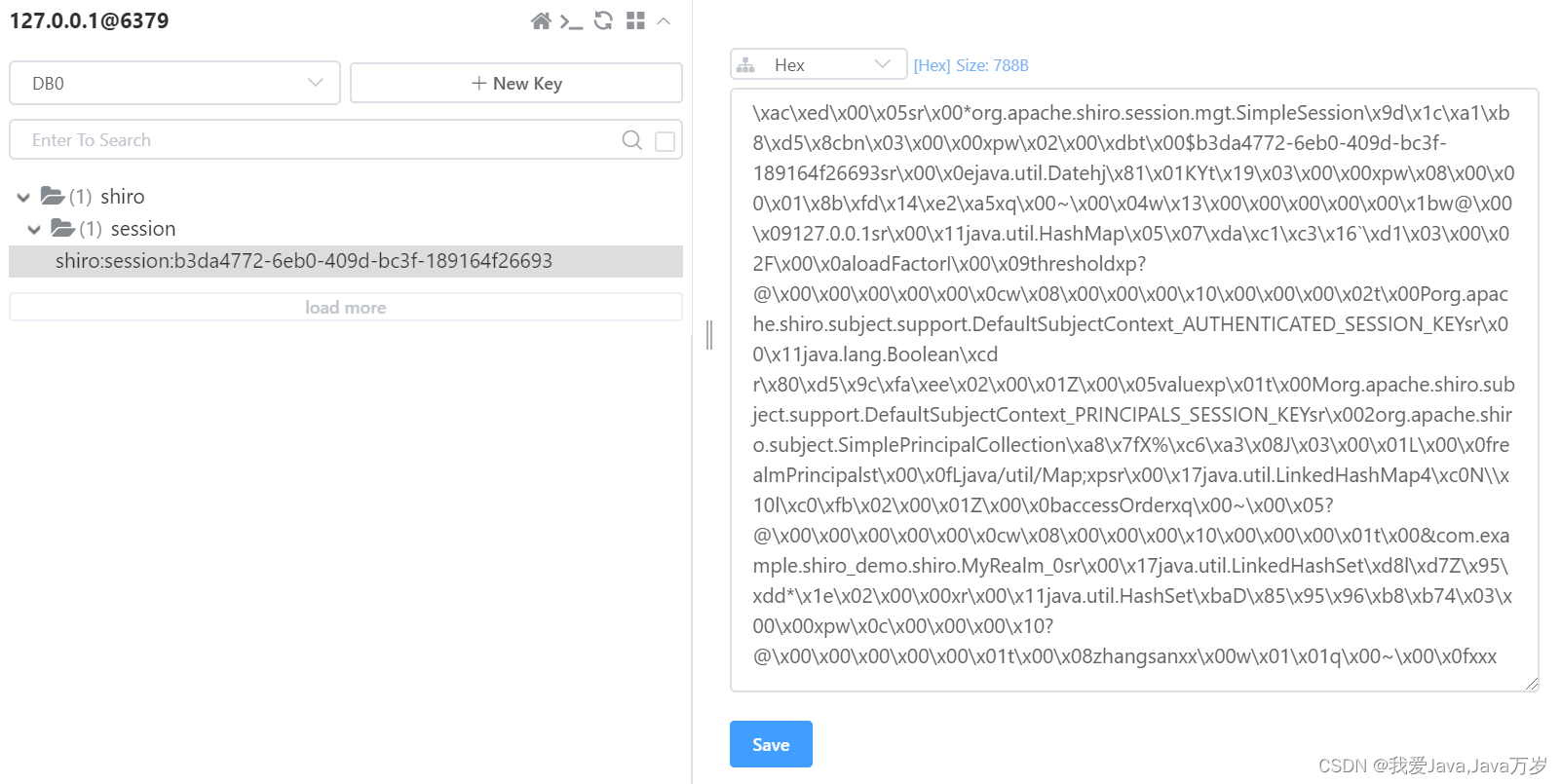
shiro整合redis
shiro整合redis 前言:shiro默认的session是存储在jvm内存中的,这样会导致java服务内存占用更大以及一旦服务器宕机或者版本迭代需要重启服务时,缓存中的数据不能恢复,导致用户需要重新登录认证,体验很差。因此利用第三…...
——@BuilderParam装饰器)
HarmonyOS(七)——@BuilderParam装饰器
前言: 前面我们认识了Builder装饰器:自定义构建函数,今天我们继续认识下一个装饰器——BuilderParam装饰器。 当开发者创建了自定义组件,并想对该组件添加特定功能时,例如在自定义组件中添加一个点击跳转操作。若直接…...
展开运算符(...)
假如我们有一个数组: const arr [7,8,9];● 我们如果想要数组中的元素,我们必须一个一个手动的去获取,如下: const arr [7,8,9]; const badNewArr [5, 6, arr[0], arr[1],arr[2]]; console.log(badNewArr);● 但是通过展开运…...
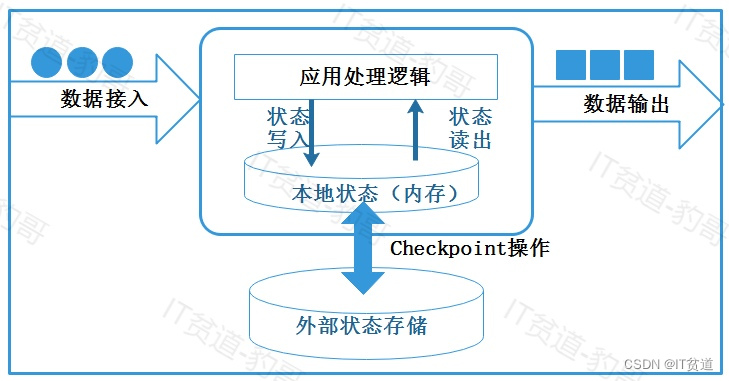
Apache Flink(二):数据架构演变
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹…...
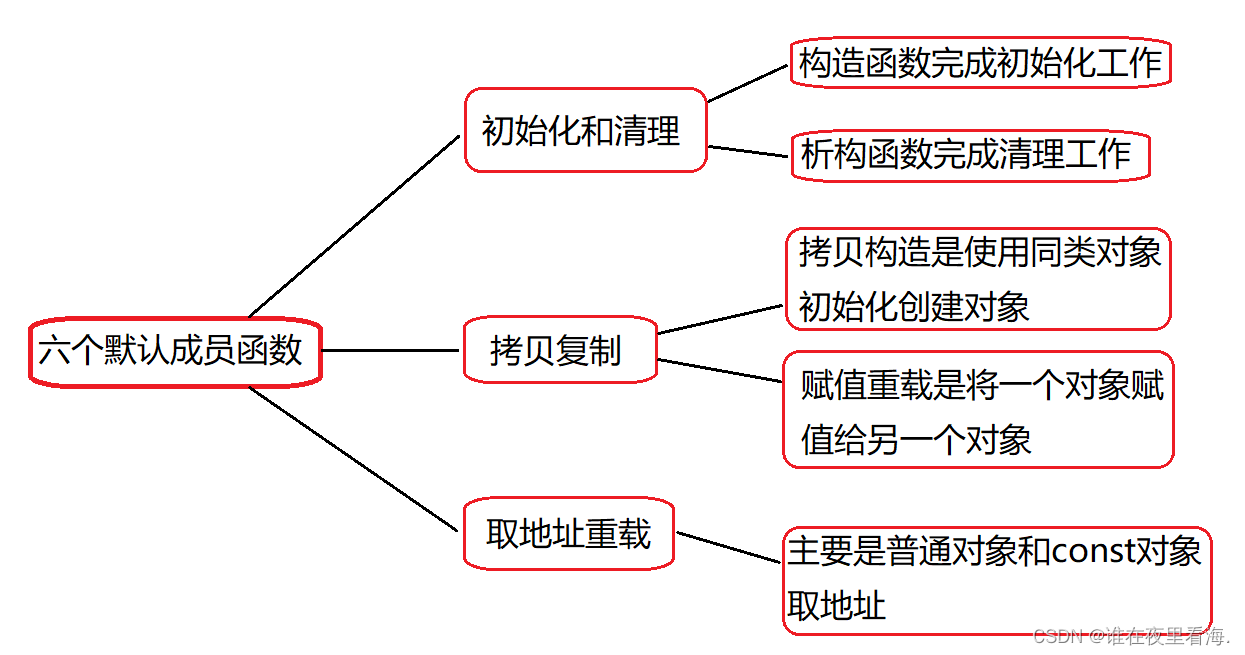
【C++】类与对象(中)
一、类的默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器会自…...

webshell之无扩展免杀
1.php加密 这里是利用phpjiami网站进行加密,进而达到加密效果 加密前: 查杀效果 可以看到这里D某和某狗都查杀 里用php加密后效果 查杀效果 可以看到这里只有D某会显示加密脚本,而某狗直接绕过 2.dezend加密 可以看到dezend加密的特征还是…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
