【数值计算方法(黄明游)】常微分方程初值问题的数值积分法:欧拉方法(向后Euler)【理论到程序】
文章目录
- 一、数值积分法
- 1. 一般步骤
- 2. 数值方法
- 二、欧拉方法(Euler Method)
- 1. 向前欧拉法(前向欧拉法)
- 2. 向后欧拉法(后向欧拉法)
- a. 基本理论
- b. 算法实现
常微分方程初值问题的数值积分法是一种通过数值方法求解给定初始条件下的常微分方程(Ordinary Differential Equations, ODEs)的问题。
一、数值积分法
1. 一般步骤
-
确定微分方程:
- 给定微分方程组 y ′ ( x ) = f ( x , y ( x ) ) y'(x) = f(x, y(x)) y′(x)=f(x,y(x))
-
确定初始条件:
- 初值问题包含一个初始条件 y ( a ) = y 0 y(a) = y_0 y(a)=y0,其中 a a a 是定义域的起始点, y 0 y_0 y0 是初始值。
-
选择数值方法:
- 选择适当的数值方法来近似解(需要考虑精度、稳定性和计算效率),常见的数值方法包括欧拉方法、改进的欧拉方法、Runge-Kutta 方法等。
-
离散化定义域:
- 将定义域 [ a , b ] [a, b] [a,b] 分割为若干小步,即选择合适的步长 h h h。通常,较小的步长能够提高数值解的精度,但也增加计算成本。
-
数值迭代:
- 使用选定的数值方法进行迭代计算:根据选择的方法,计算下一个点的函数值,并更新解。
-
判断停止条件:
- 判断是否达到满足指定精度的近似解:可以使用某种误差估计方法,例如控制局部截断误差或全局误差。
-
输出结果:
- 最终得到在给定定义域上满足初值问题的近似解。
2. 数值方法
-
欧拉方法(Euler Method):
- 基本思想:根据微分方程的定义,使用离散步长逼近导数,进而逼近下一个点的函数值。
- 公式: y n + 1 = y n + h f ( t n , y n ) y_{n+1} = y_n + h f(t_n, y_n) yn+1=yn+hf(tn,yn)
其中, y n y_n yn是第 n n n 步的函数值, h h h是步长, f ( t n , y n ) f(t_n, y_n) f(tn,yn) 是在点 ( t n , y n ) (t_n, y_n) (tn,yn) 处的导数。
-
改进的欧拉方法(Improved Euler Method 或梯形法 Trapezoidal Rule):
- 基本思想:使用两次近似来提高精度,首先使用欧拉方法计算中间点,然后用该点的导数估计值来计算下一个点。
- 公式: y n + 1 = y n + h 2 [ f ( t n , y n ) + f ( t n + 1 , y n + h f ( t n , y n ) ) ] y_{n+1} = y_n + \frac{h}{2} [f(t_n, y_n) + f(t_{n+1}, y_n + hf(t_n, y_n))] yn+1=yn+2h[f(tn,yn)+f(tn+1,yn+hf(tn,yn))]
-
Runge-Kutta 方法:
- 基本思想:通过多个阶段的计算来提高精度。其中最常见的是四阶 Runge-Kutta 方法。
- 公式:
k 1 = h f ( t n , y n ) k_1 = hf(t_n, y_n) k1=hf(tn,yn) k 2 = h f ( t n + h 2 , y n + k 1 2 ) k_2 = hf(t_n + \frac{h}{2}, y_n + \frac{k_1}{2}) k2=hf(tn+2h,yn+2k1) k 3 = h f ( t n + h 2 , y n + k 2 2 ) k_3 = hf(t_n + \frac{h}{2}, y_n + \frac{k_2}{2}) k3=hf(tn+2h,yn+2k2) k 4 = h f ( t n + h , y n + k 3 ) k_4 = hf(t_n + h, y_n + k_3) k4=hf(tn+h,yn+k3) y n + 1 = y n + 1 6 ( k 1 + 2 k 2 + 2 k 3 + k 4 ) y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) yn+1=yn+61(k1+2k2+2k3+k4)
这些方法中,步长 h h h 是一个关键参数,它决定了离散化的程度,选择合适的步长对于数值解的准确性和稳定性非常重要。
二、欧拉方法(Euler Method)
1. 向前欧拉法(前向欧拉法)
【计算方法与科学建模】常微分方程初值问题的数值积分法:欧拉方法(向前Euler及其python实现)
- 向前差商近似微商:
- 在节点 X n X_n Xn 处,通过向前差商 y ( X n + 1 ) − y ( X n ) h \frac{y(X_{n+1}) - y(X_n)}{h} hy(Xn+1)−y(Xn) 近似替代微分方程 y ′ ( x ) = f ( x , y ( x ) ) y'(x) = f(x, y(x)) y′(x)=f(x,y(x)) 中的导数项,得到 y ′ ( X n ) ≈ y ( X n + 1 ) − y ( X n ) h = f ( X n , y ( X n ) ) y'(X_n) \approx \frac{y(X_{n+1}) - y(X_n)}{h} = f(X_n, y(X_n)) y′(Xn)≈hy(Xn+1)−y(Xn)=f(Xn,y(Xn))
- 这个近似通过将差商等于导数的思想,将微分方程转化为递推关系式。
- 递推公式:
- 将上述近似公式改为等式,得到递推公式 y n + 1 = y n + h f ( X n , y n ) y_{n+1} = y_n + hf(X_n, y_n) yn+1=yn+hf(Xn,yn)
- 这个公式是 Euler 方法的核心,通过这个公式可以逐步计算得到近似解的数值。
2. 向后欧拉法(后向欧拉法)
a. 基本理论
向后 Euler 方法的核心思想是从微分方程的 y ′ ( X n + 1 ) = f ( x n + 1 , y ( X n + 1 ) ) y'(X_{n+1}) = f(x_{n+1}, y(X_{n+1})) y′(Xn+1)=f(xn+1,y(Xn+1)) 出发,使用向后差商 y ( X n + 1 ) − y ( X n ) h \frac{y(X_{n+1}) - y(X_n)}{h} hy(Xn+1)−y(Xn) 近似微商 y ′ ( X n + 1 ) y'(X_{n+1}) y′(Xn+1),然后通过这个近似来得到递推公式。具体而言,递推公式为:
y n + 1 = y n + h f ( X n + 1 , y n + 1 ) , n = 0 , 1 , … y_{n+1} = y_n + hf(X_{n+1}, y_{n+1}), \quad n = 0, 1, \ldots \ yn+1=yn+hf(Xn+1,yn+1),n=0,1,…
这里, y n + 1 y_{n+1} yn+1 是在 X n + 1 X_{n+1} Xn+1 处的近似解, h h h 是步长。
对比向前 Euler 方法和向后 Euler 方法,可以注意到两者的关键区别:
-
显式 vs. 隐式:
- 向前 Euler 方法给出了一个显式的递推公式,可以直接计算 y n + 1 y_{n+1} yn+1。
- 向后 Euler 方法给出了一个隐式的递推公式,其中 y n + 1 y_{n+1} yn+1出现在方程的右侧,需要通过求解非线性方程来获得。
-
求解方式:
- 向前 Euler 方法的解可以通过简单的迭代计算得到。
- 向后 Euler 方法的解需要通过迭代求解非线性方程,通常,可以使用迭代法,如牛顿迭代法,来逐步逼近方程的解。
-
具体的迭代过程:
-
初始值:使用向前 Euler 公式给出一个初值,例如 y n + 1 ( 0 ) = y n + h f ( x n + 1 , y n ) y_{n+1}^{(0)} = y_n + hf(x_{n+1}, y_n) yn+1(0)=yn+hf(xn+1,yn),其中 y n + 1 ( 0 ) y_{n+1}^{(0)} yn+1(0) 是迭代的初值。
-
迭代公式:使用迭代公式 y n + 1 ( k + 1 ) = y n + h f ( x n + 1 , y n + 1 ( k ) ) , k = 0 , 1 , … y_{n+1}^{(k+1)} = y_n + hf(x_{n+1}, y_{n+1}^{(k)}), \quad k = 0, 1, \ldots yn+1(k+1)=yn+hf(xn+1,yn+1(k)),k=0,1,…计算 y n + 1 y_{n+1} yn+1 的逼近值。
-
重复迭代,直到满足收敛条件,得到 y n + 1 y_{n+1} yn+1 的近似解。
-
向后 Euler 方法在处理某些问题(例如刚性问题)时可能更为稳定,但由于涉及隐式方程的求解,其计算成本可能较高。
b. 算法实现
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolvedef forward_euler(f, y0, a, b, h):"""使用向前欧拉法求解一阶常微分方程初值问题Parameters:- f: 函数,表示微分方程的右侧项,形式为 f(x, y)- y0: 初始条件,表示在 x=a 处的函数值- a: 区间起点- b: 区间终点- h: 步长Returns:- x_values: 区间 [a, b] 上的离散节点- y_values: 对应节点上的函数值的近似解"""num_steps = int((b - a) / h) + 1 # 计算步数x_values = np.linspace(a, b, num_steps) # 生成离散节点y_values = np.zeros(num_steps) # 初始化结果数组y_values[0] = y0 # 设置初始条件# 使用向前欧拉法进行逐步迭代for i in range(1, num_steps):x = x_values[i - 1]y = y_values[i - 1]y_values[i] = y + h * f(x, y)return x_values, y_valuesdef backward_euler(f, y0, a, b, h):"""使用向后欧拉法求解一阶常微分方程初值问题Parameters:- f: 函数,表示微分方程的右侧项,形式为 f(x, y)- y0: 初始条件,表示在 x=a 处的函数值- a: 区间起点- b: 区间终点- h: 步长Returns:- x_values: 区间 [a, b] 上的离散节点- y_values: 对应节点上的函数值的近似解"""num_steps = int((b - a) / h) + 1 # 计算步数x_values = np.linspace(a, b, num_steps) # 生成离散节点y_values = np.zeros(num_steps) # 初始化结果数组y_values[0] = y0 # 设置初始条件# 使用向后欧拉法进行逐步迭代for i in range(1, num_steps):x = x_values[i]# 定义非线性方程equation = lambda y_next: y_next - y_values[i - 1] - h * f(x, y_next)# 利用 fsolve 求解非线性方程,得到 y_values[i]y_values[i] = fsolve(equation, y_values[i - 1])[0]return x_values, y_values# 示例:求解 y' = y -2x/y,初始条件 y(0) = 1 在区间 [0, 1] 上的近似解
def example_function(x, y):return y - 2 * x / ya, b = 0, 1 # 区间 [a, b]
y0 = 1 # 初始条件 y(0) = 1
h = 0.05 # 步长
x_values0, y_values0 = forward_euler(example_function, y0, a, b, h)x_values, y_values = backward_euler(example_function, y0, a, b, h)# 绘制结果
plt.plot(x_values0, y_values0, label='Forward Euler')
plt.plot(x_values, np.sqrt(1 + 2 * x_values), label='Exact Solution')
plt.plot(x_values, y_values, label='Backward Euler')
plt.title('h = {}'.format(h))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()-
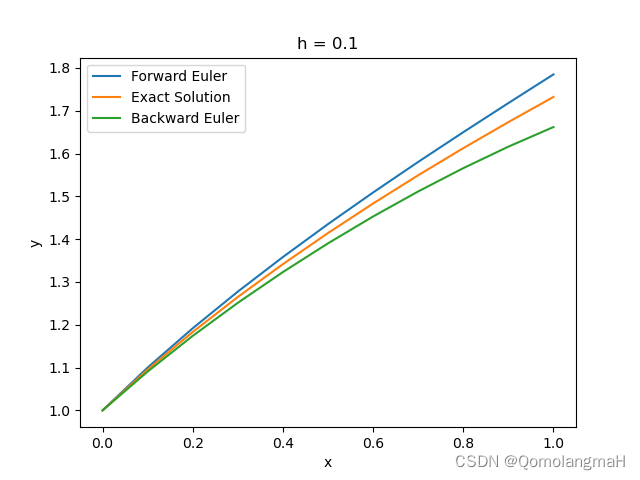
h = 0.1
-
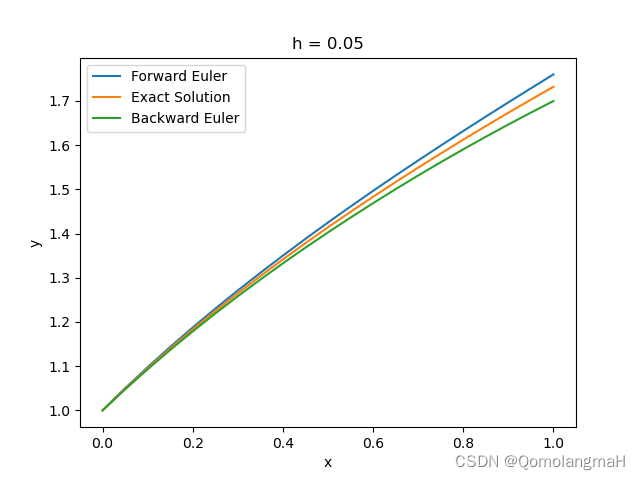
h = 0.05
-
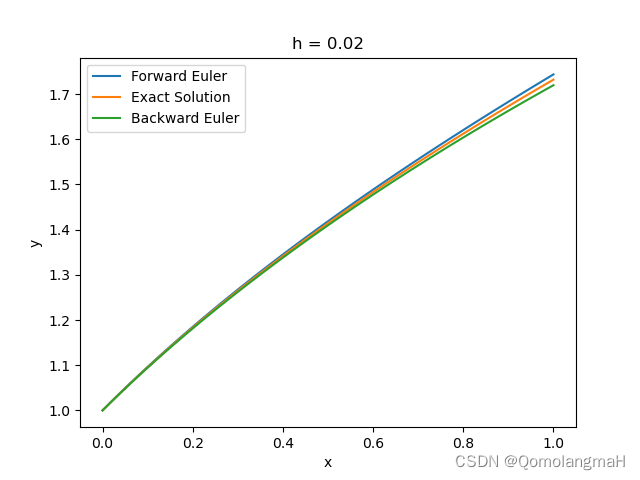
h = 0.02
相关文章:

【数值计算方法(黄明游)】常微分方程初值问题的数值积分法:欧拉方法(向后Euler)【理论到程序】
文章目录 一、数值积分法1. 一般步骤2. 数值方法 二、欧拉方法(Euler Method)1. 向前欧拉法(前向欧拉法)2. 向后欧拉法(后向欧拉法)a. 基本理论b. 算法实现 常微分方程初值问题的数值积分法是一种通过数值方…...

mac安装homebrew/brew遇到443
文章目录 问题描述解决方法方法一方法二 参考文献 问题描述 brew 全称Homebrew 是Mac OSX上的软件包管理工具 想在mac终端安装,运行网上提供的指令 /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install.sh)&quo…...
VSCODE 在新窗口中打开
使用VS习惯了,经常在新窗口中打开查看 但是VSCODE,无法拖动标签到一个新窗口中,一直以为没这个功能 后来发现 使用快捷健 ctlk,o 可以将标签页在新窗口中打开,虽然不如vsstudio方便,不过也可实现在新窗口打开的功能…...

Python与设计模式--解释器模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
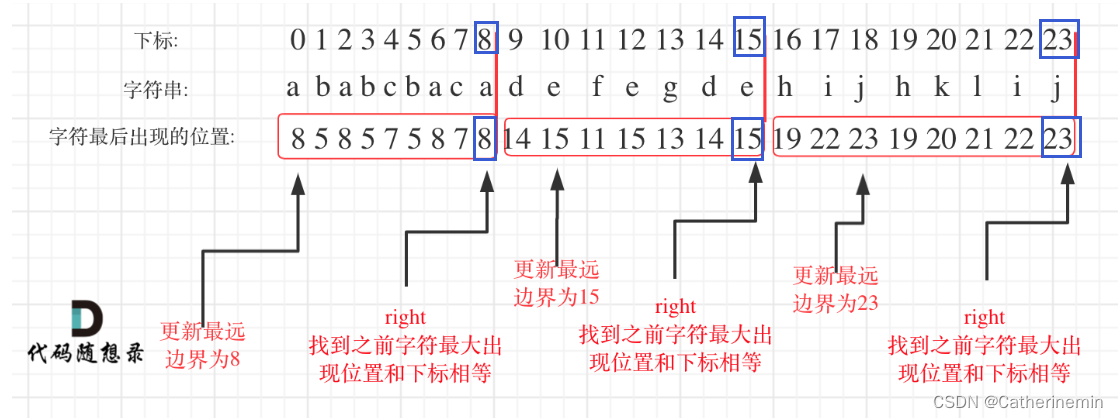
代码随想录算法训练营第36天| 435. 无重叠区间 763.划分字母区间 56. 合并区间
JAVA代码编写 435. 无重叠区间 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。 示例 1: 输入: intervals [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后&#x…...
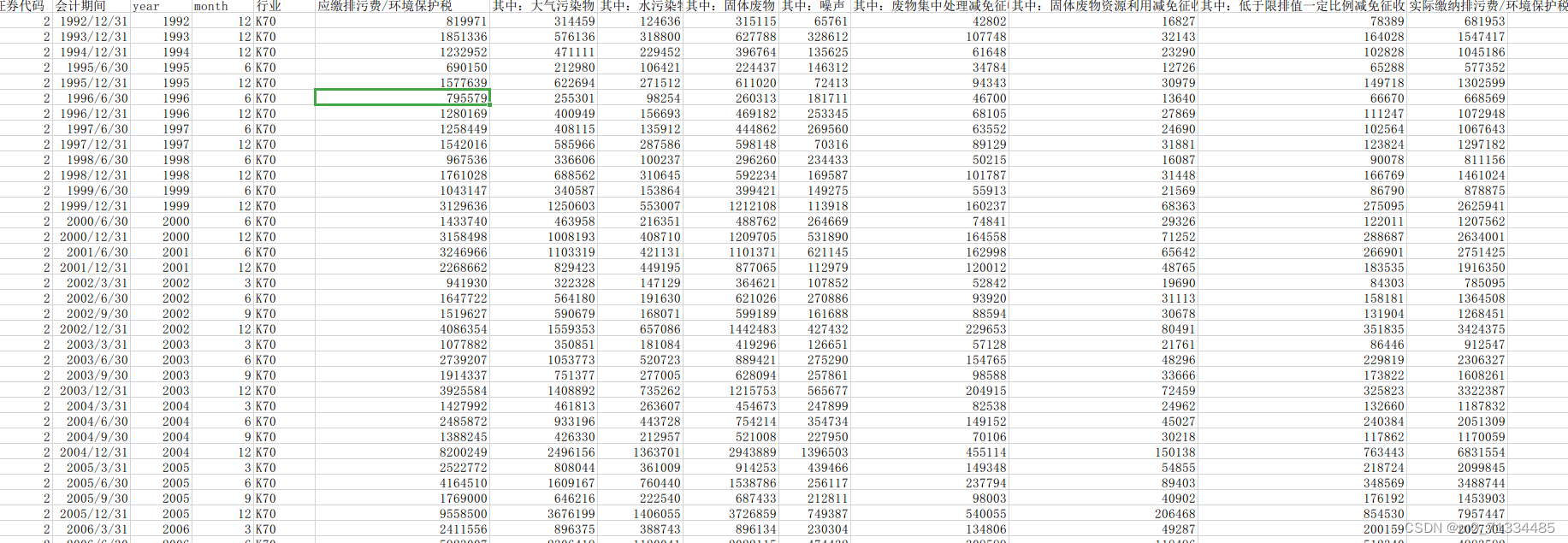
1990-2021年上市公司排污费和环境保护税数据
1990-2021年上市公司排污费和环境保护税数据 1、时间:1990-2021年 2、指标: 证券代码、会计期间、year、month、行业、应缴排污费/环境保护税、其中:大气污染物、其中:水污染物、其中:固体废物、其中:噪…...
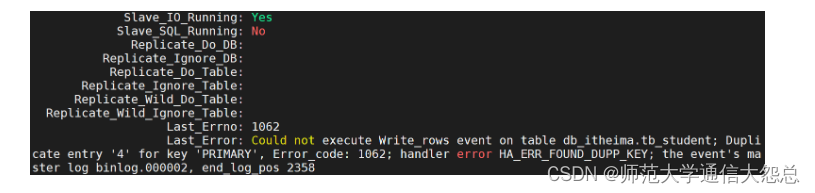
MySQL主从复制架构
MySQL主从复制架构 一、MySQL集群概述 ##1、集群的主要类型 高可用集群(High Available Cluster,HA Cluster) 高可用集群是指通过特殊的软件把独立的服务器连接起来,组成一个能够提供故障切换(Fail Over)…...
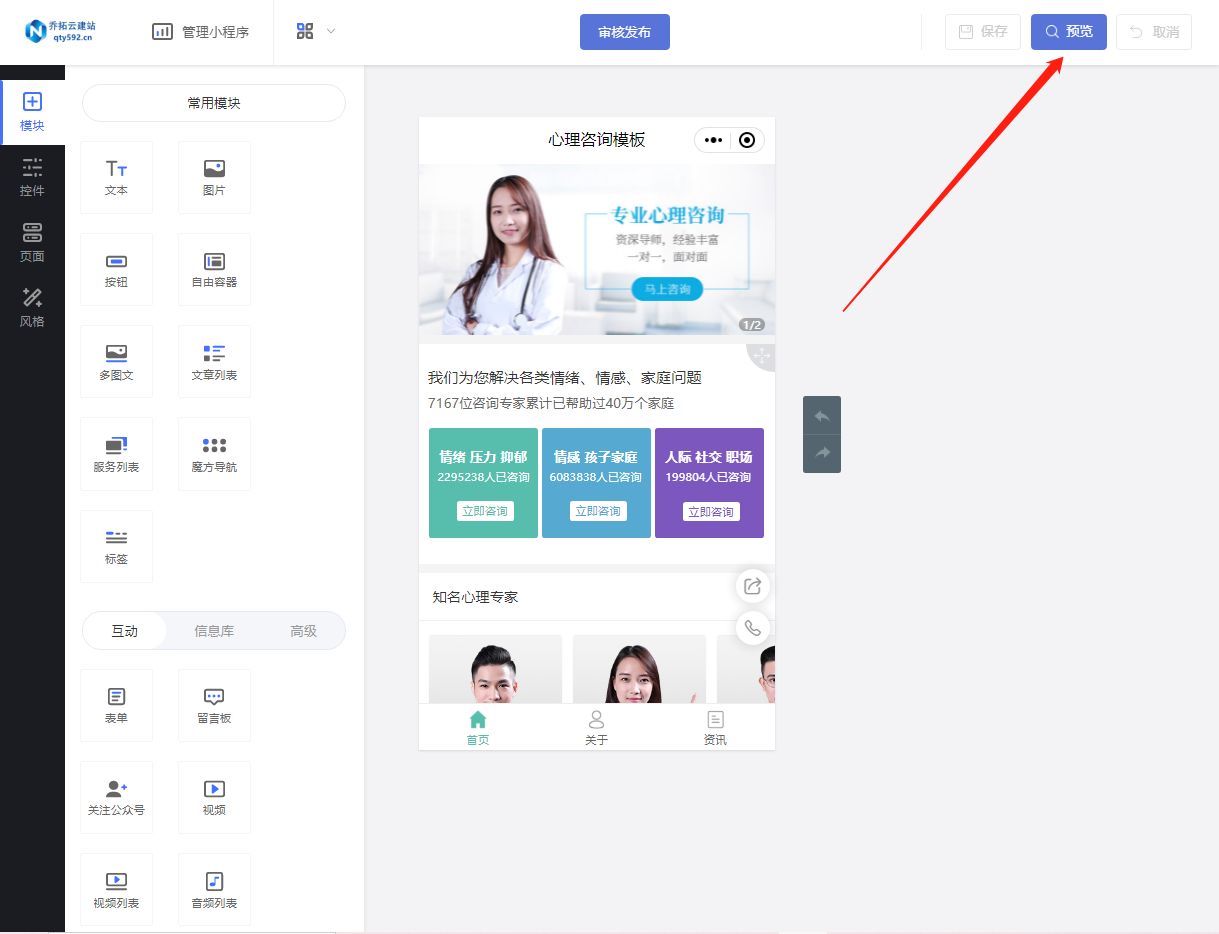
制作心理咨询小程序的详细指南
随着科技的的发展,小程序已经成为了人们日常生活中不可或缺的一部分。特别是在心理咨询这个领域,小程序可以提供一个更为便捷、高效的服务平台。本文将通过乔拓云平台为例,详细介绍如何制作一个心理咨询小程序。 首先,我们需要注册…...

Apache httpd-2.4安装并配置转发
目录 一、写在前面二、下载Apache三、编译安装依赖库3.1 编译安装apr3.2 编译安装apr-util3.3 编译安装pcre 四、编译安装及启动Apache4.1 编译安装Apache4.2 启动Apache 五、配置Apache5.1 备份 httpd.conf5.2 启用代理模块5.3 修改监听端口5.4 配置转发规则 六、常用指令6.1 …...
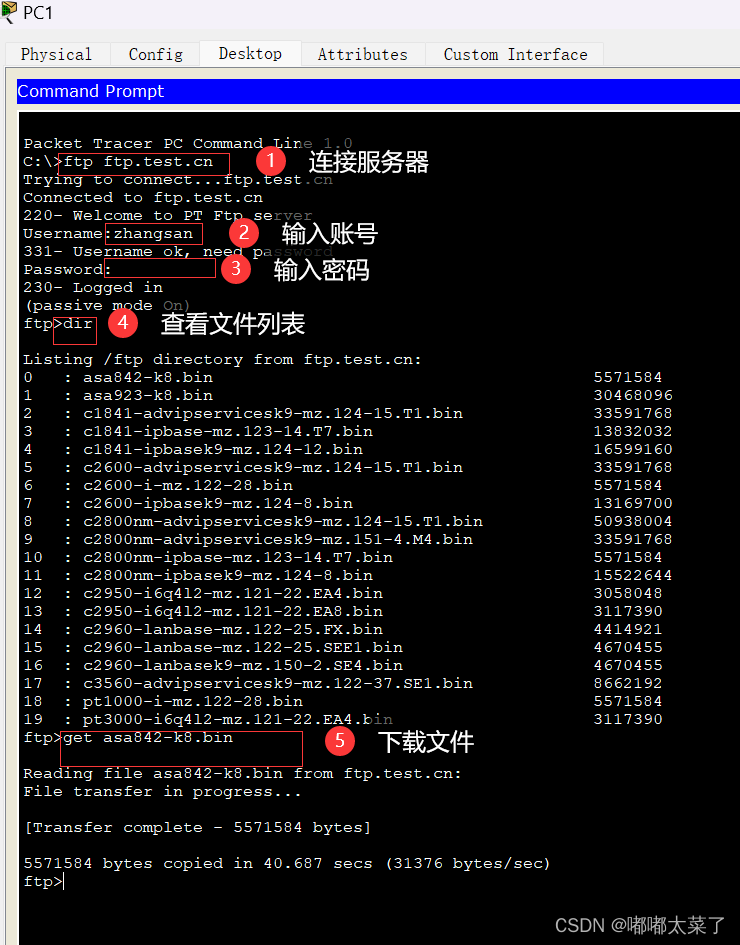
【Cisco Packet Tracer】DHCP/FTP/WEB/DNS实验
本文使用CiscoPacketTracer仿真软件实现了DHCP/FTP/WEB/DNS实验,拓扑中包含2个客户机和3个服务器(DHCP服务器、DNS服务器、FTP/WEB公用一个服务器),客户机的IP地址由DHCP服务器动态分配。 DHCP服务器IP地址:192.168.0…...

模糊C均值聚类(Fuzzy C-means clustering,FCM)的基本概念,详细流程以及广泛应用!
文章目录 1.基本概念2. FCM的详细流程3.FCM的应用 1.基本概念 模糊C均值聚类(Fuzzy C-means clustering,FCM)是一种软聚类方法,它允许数据点属于多个聚类中心,每个聚类中心都有一个权重。与传统的硬聚类方法ÿ…...

chapter10-homework-Java
第十章作业 Homework01知识点 Homework02知识点 Homework03知识点 Homework04知识点 Homework05知识点 Homework06Homework07Homework08 Homework01 分析执行结果。 public static void main(String[] args) {Car_ c new Car_();Car_ c1 new Car_(100);System.out.println(…...
)
前端如何中断请求 ( axios、原生 ajax、fetch)
使用场景 在前端开发中,我们经常需要中断请求来优化性能或处理特定的业务需求。以下是一些常见的使用场景: 比如 重复请求:当页面中多个组件并发调用同一个接口时,在第一个请求返回后,我们可能需要中断其他组件对该接…...

CSS实现一些小功能
1.信封边框的实现 1.1 使用背景渐变 <!DOCTYPE html><html><head><meta charset"UTF-8"><title></title><style type"text/css">.uu {width: 200px;height: 70px;padding:1em;border: 1em solid transparent;…...

Ubuntu安装nfs服务步骤
Ubuntu安装nfs服务步骤 一、NFS? NFS:网络文件系统(Network File system File)缩写,可通过网络让不同的机器,不同操作系统之间可以彼此共享文件和目录。 二、安装 1.安装nfs服务器命令:sudo…...

android开发:子线程更新UI界面
多线程操作经常希望在子线程更新界面,这样方便调试,但是,但是经常这样做程序就不对劲了,为什么呢?因为为了保证界面流畅,不允许在非UI线程直接操作界面,只能通过一些专门途径进行。另外…...
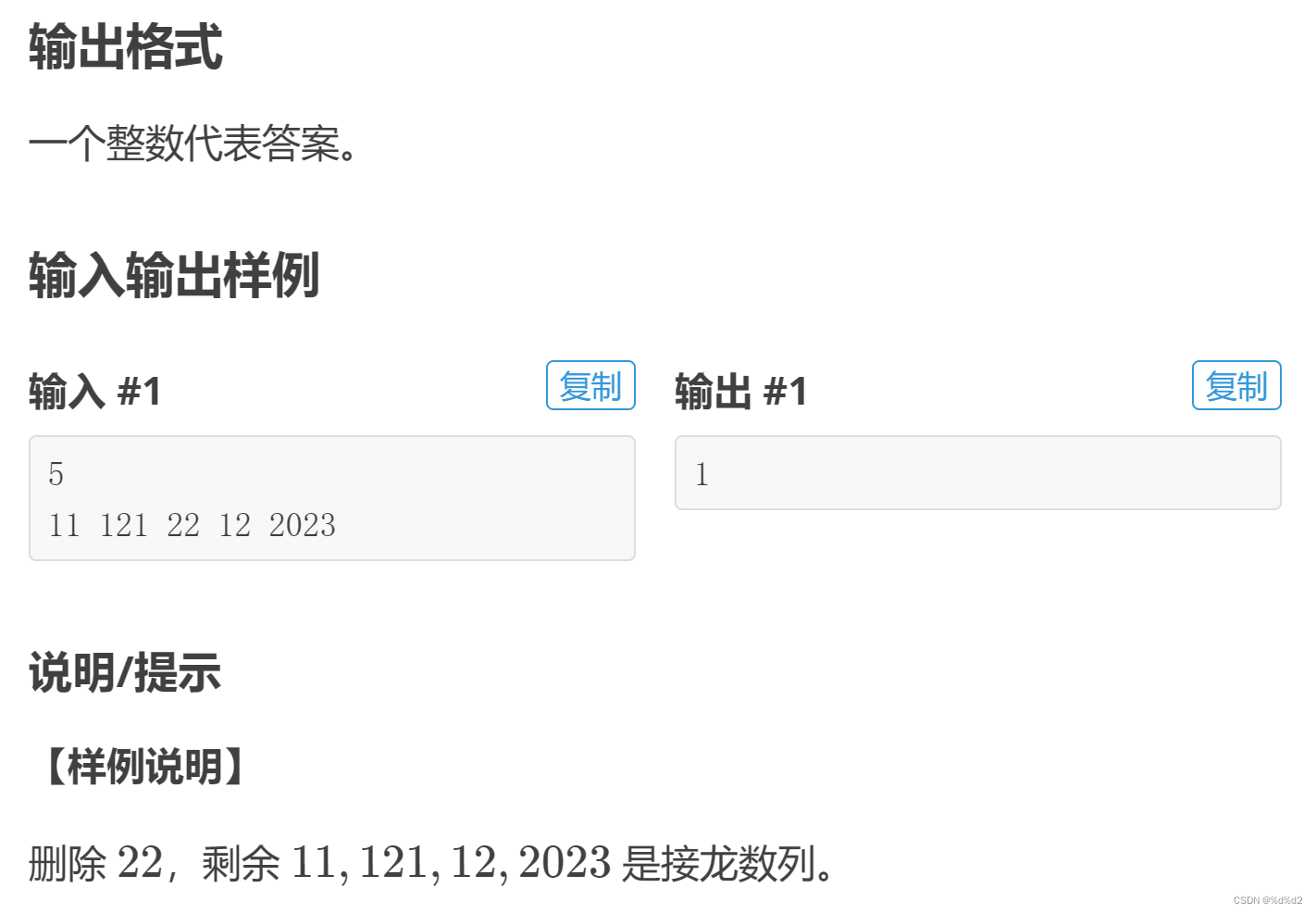
P9242 [蓝桥杯 2023 省 B] 接龙数列(dp+最长接龙序列+分类)
1. 计算0~9为结尾的最长子串长度 2. 对于每个数字,比较其开头可连接子串长度1 与 原来以其末位为末尾的子串长度 3. 更新以其末位为末尾的子串长度 #include<iostream> #include<string.h>using namespace std;// 相当于记录…...
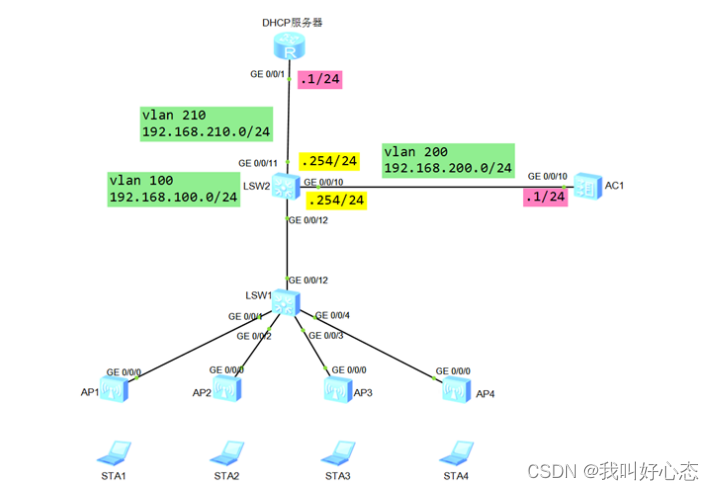
网络运维与网络安全 学习笔记2023.11.29
网络运维与网络安全 学习笔记 第三十天 今日更新太晚啦!!! 主要是今天工作时挨了一天骂,服了,下次记得骂的轻一点!!! (要不是为了那点微薄的薪资,谁愿意听你…...

Java实现通过经纬度求两个任意地点在球面上的距离
我们在实际开发中会获取对应的经纬度,可以使用ES大数据搜索引擎进行计算对应区域的数据,那我们在如何根据两个经纬度获取对应的球面距离,就是在地球上从一个地点到另一个地点的直线距离 工具类如下: public class GeoUtils {// 地球半径&am…...

vscode使用插件KoroFileHeader添加注释
一、简介 KoroFileHeader 是一款用于在 VSCode 中用于生成文件头部注释和函数注释的插件,支持所有主流语言,功能强大,灵活方便,文档齐全。 VSCode 安装 KoroFileHeader 好插件,就可以直接使用。 "fileheader.cu…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
