数据结构 -- 图论之最小生成树
目录
1.最小生成树算法
1.Kruskal算法
2.Prim算法
1.最小生成树算法
定义:最小生成树算法:连通图有n个顶点组成,那么此时的图的每一个点都能相互连接并且边的个数为n-1条,那么此时该图就是最小生成树.
下面量算法有几个共同的特点:
1.只能使用图中权值最小的边来构造生成树
2.只能使用恰好n-1条边构造生成树
3.n-1条边的图不能存在回路
4.Kruskal和Prim两个算法都采用了逐步求解的贪心策略
1.Kruskal算法
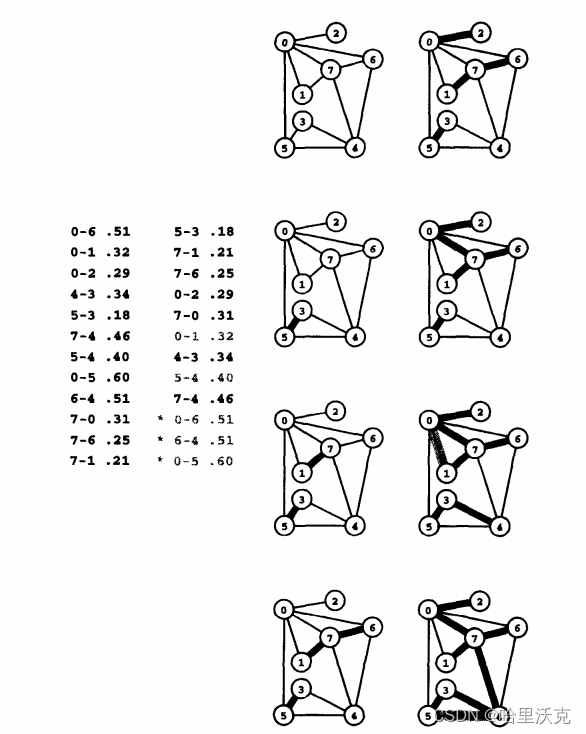
任给一个有n个顶点的连通网络N={V,E},首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量,其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量,则将此边加入到G中。如此重复,直到所有顶点在同一个连通分量上为止。核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。
//数组的下标添加边void _AddEdge(size_t srci, size_t dsti, const W& w){_matrix[srci][dsti] = w;// 无向图if (Direction == false){_matrix[dsti][srci] = w;}}struct Edge{size_t _srci;size_t _dsti;W _w;Edge(size_t srci, size_t dsti, const W& w):_srci(srci), _dsti(dsti), _w(w){}bool operator>(const Edge _edge)const{return _w > e._w;}};W Kruskal(Self& minTree){size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}priority_queue<Edge, vector<Edge>, greater<Edge>> minque;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (i < j && _matrix[i][j] != MAX_W){minque.push(Edge(i, j, _matrix[i][j]));}}}int size = 0;W totalW = W();UnionFindSet ufs(n);while (!minque.empty()){Edge min = minque.top();minque.pop();if (!ufs.InSet(min._srci, min._dsti)){minTree._AddEdge(min._srci, min._dsti, min._w);ufs.Union(min._srci, min._dsti);++size;totalW += min._w;}}if (size == n - 1)return totalW;elsereturn W();}2.Prim算法
1.从源点出发,将所有与源点连接的点加入一个待处理的集合中
2.从集合中找出与源点的边中权重最小的点,从待处理的集合中移除标记为确定的点
3.将找到的点按照步骤1的方式处理
4.重复2,3步直到所有的点都被标记
(重点是不需要并查集来判断是否成环,因为两个集合就天然区分是否成环的因素)
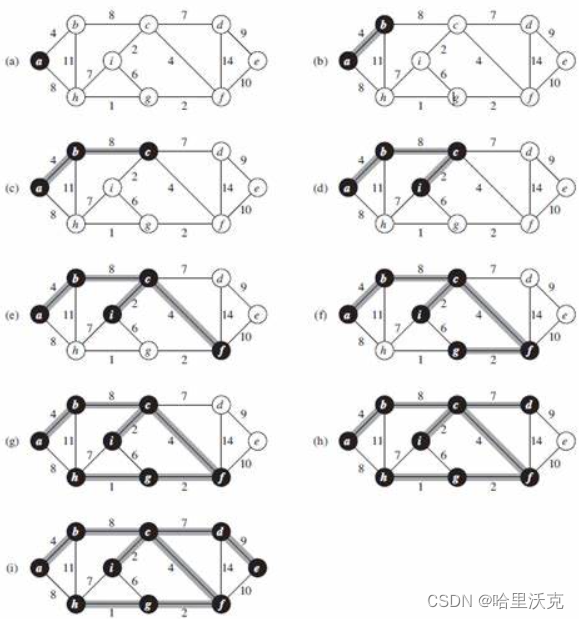
W Prim(Self& minTree,const V& src){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();minTree._vertexs = _vertexs;minTree._indexMap = _indexMap;minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, MAX_W);}vector<bool> X(n, false);vector<bool> Y(n, true);X[srci] = true;Y[srci] = false;priority_queue<Edge, vector<Edge>, greater<Edge>> minq;for (int i = 0; i < n; ++i){if (_matrix[srci][i] != MAX_W){minq.push(Edge(srci, i, _matrix[srci][i]);}}size_t num = 0;W sum = W();while (!minq.empty()){Edge min = minq.top();minq.pop();if (!X[min._dsti]){minTree.AddEdge(min._srci, min._dsti, min._w);X.insert(min._dsti);Y.erase(min._dsti);++num;sum += min._w;if (num == n - 1) break;for (int i = 0; i < n; ++i){if (_matrix[min._dsti][i] != MAX_W && Y[i]){minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]);}}}}if (num == n - 1)return sum;elsereturn W();}
相关文章:
数据结构 -- 图论之最小生成树
目录 1.最小生成树算法 1.Kruskal算法 2.Prim算法 1.最小生成树算法 定义:最小生成树算法:连通图有n个顶点组成,那么此时的图的每一个点都能相互连接并且边的个数为n-1条,那么此时该图就是最小生成树. 下面量算法有几个共同的特点: 1.只能使用图中权值最小的边来构造生成树 …...

【已解决】游戏缺少xinput1_3.dll的详细解决方案与详情解析
在现代科技日新月异的时代,电脑已经成为我们生活和工作中不可或缺的工具。然而,由于各种原因,电脑可能会出现一些问题,其中之一就是xinput1_3.dll文件的缺失。本文将详细介绍xinput1_3.dll丢失对电脑的影响以及丢失的原因…...
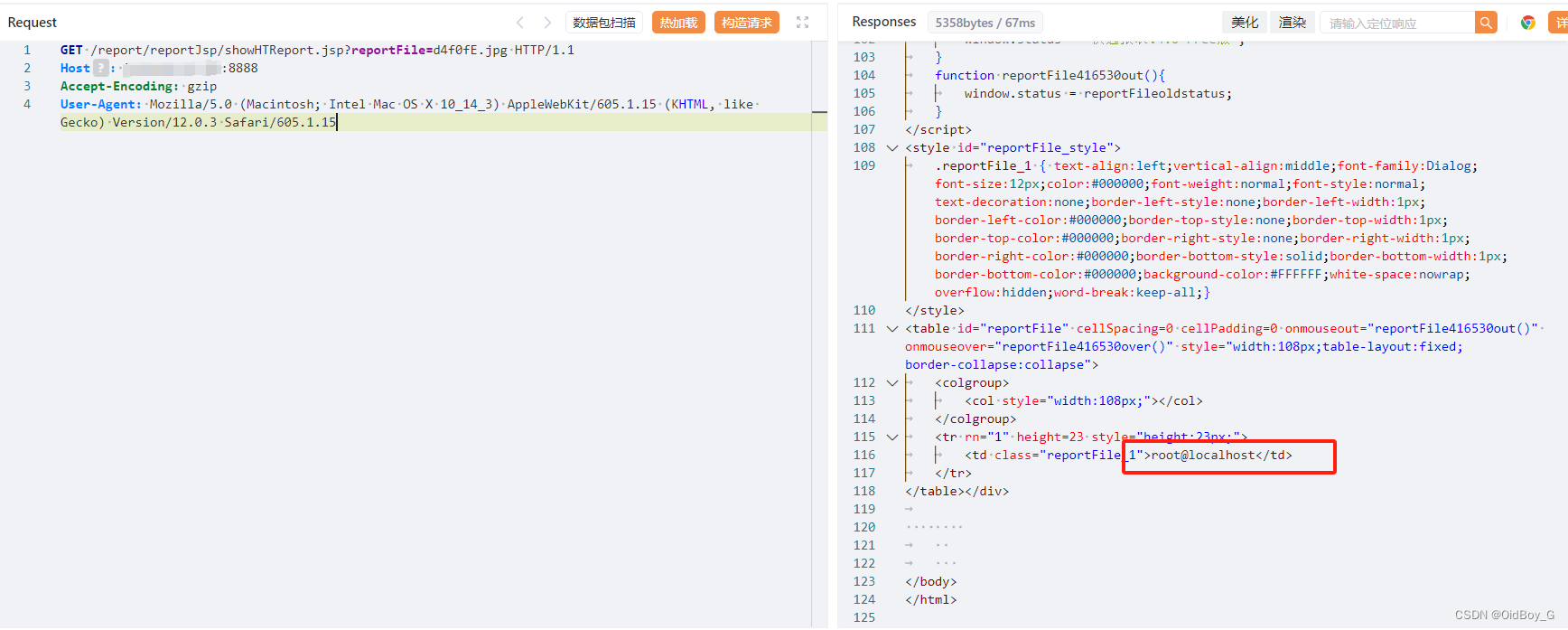
华天动力-OA8000 MyHttpServlet 文件上传漏洞复现
0x01 产品简介 华天动力OA是一款将先进的管理思想、 管理模式和软件技术、网络技术相结合,为用户提供了低成本、 高效能的协同办公和管理平台。 0x02 漏洞概述 华天动力OA MyHttpServlet 存在任意文件上传漏洞,未经身份认证的攻击者可上传恶意的raq文件…...

小航助学题库蓝桥杯题库c++选拔赛(23年8月)(含题库教师学生账号)
需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号) 需要在线模拟训练的题库账号请点击 小航助学编程在线模拟试卷系统(含题库答题软件账号)...

[Ubuntu 18.04] RK3399搭建NFS服务实现共享目录
NFS(Network File System)是一种分布式文件系统协议,允许远程计算机通过网络访问存储在另一台计算机上的文件。它使得多台计算机可以共享文件,并且可以在不同计算机之间实现文件的透明访问和共享。 以下是 NFS 服务器的一些特点和介绍: 文件共享:NFS 服务器允许将存储在…...

Java---抽象类讲解
文章目录 1. 抽象类概述2. 抽象类特点3. 抽象类的成员特点4. 抽象类猫狗应用 1. 抽象类概述 在Java中,一个没有方法体的方法应该定义为抽象方法;而类中如果有抽象方法,该类必须定义为抽象类。 2. 抽象类特点 1. 抽象类和抽象方法必须使用abst…...

CNAS认可是什么?CNAS软件测试报告如何获取?
一、CNAS认可是什么? CNAS认可是指中国合格评定国家认可委员会的认可程序。CNAS是中国最高级别的认可机构,负责审核和认可符合国家标准的实验室、检测机构和认证机构。通过CNAS认可,机构可以获得国际公认的认可证书,证明其测试结果和认证…...

Tomcat 修改版本号
lib 目录下增加文件 /lib/org/apache/catalina/util/ServerInfo.properties ServerInfo.properties文件里面只需要输入server.info显示的版本号 其他可配置信息 server.infonginx server.number22.0 server.builtMay 11 2023 08:22:10 UTC 显示效果...

Python算法——霍夫曼编码树
Python中的霍夫曼编码树 霍夫曼编码是一种用于数据压缩的技术,通过构建霍夫曼编码树(Huffman Tree)来实现。这篇博客将详细讲解霍夫曼编码树的原理、构建方法和使用方式,并提供相应的Python代码实现。 霍夫曼编码原理 霍夫曼编…...

hql面试题之上海某资深数仓开发工程师面试题-求不连续月份的月平均值
1.题目 A,B两组产品的月平均值,月平均值是当月的前三个月值的一个平均值,注意月份是不连续的,如果当月的前面的月份不存在,则为0。如A组2023-04的月平均值为2023年1月的数据加2023-02月的数据的平均值,因为没有其他月…...
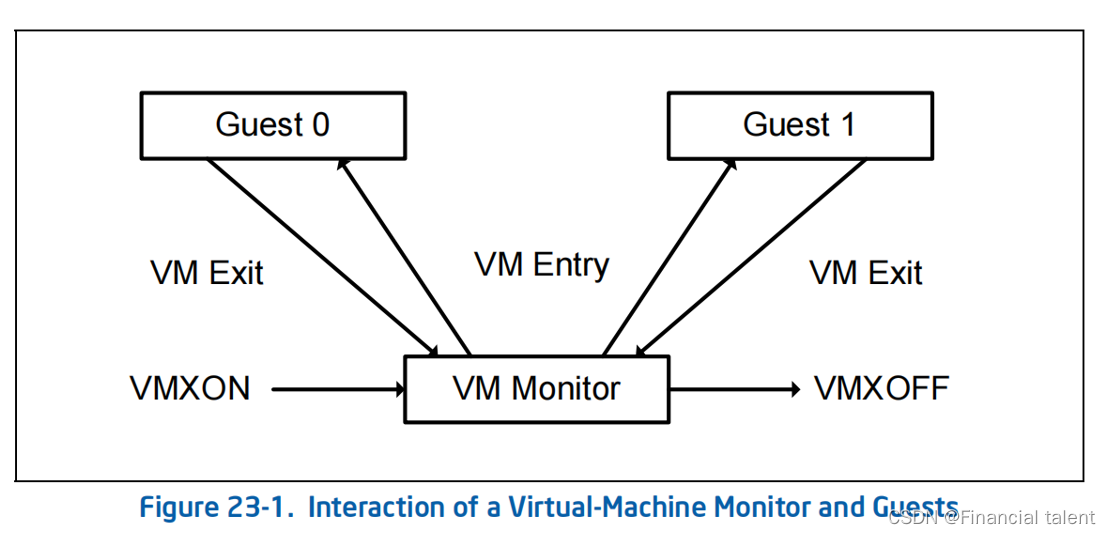
VT驱动开发
VT技术(编写一个VT框架) 1.VT技术介绍 1.技术介绍 1.VT技术 VT技术是Intel提供的虚拟化技术,全称为Intel Virtualization Technology。它是一套硬件和软件的解决方案,旨在增强虚拟化环境的性能、可靠性和安全性。VT技术允许在一台物理计算机上同时运…...

火柴人版王者-Java
主类 package com.sxt; import com.sxt.beast.Beast; import java.awt.Component; import java.awt.Graphics; import java.awt.Image; import java.awt.Toolkit; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.KeyAdapter…...

docker 中的–mount 和-v 参数有啥区别
docker 中的–mount 和-v 参数有啥区别 --mount 和 -v 是 Docker 中用于挂载卷(Volumes)的两种不同的方式。 --mount 参数: 这是一种更为灵活和强大的挂载方式,允许你指定多个选项。 使用 --mount 参数,你可以指定挂…...
设计规则:模块化的力量
这是一本比较冷门的书**《设计规则:模块化的力量》**,虽然豆瓣上只有58个评价,但是确实能学到很多东西。 这本书对我非常深远。不是是投资,创业,还是其他领域,模块化思想都能帮上你。这本书告诉我们生万物…...
)
数据结构与算法之递归: LeetCode 78. 子集 (Typescript版)
子集 https://leetcode.cn/problems/subsets/ 描述 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1 输入:nums [1,2,3]…...
C# 使用 Fody 监控方法执行时间
写在前面 在做性能调优的时候,经常需要跟踪具体方法的执行时间;通过插入Stopwatch的方案对代码的侵入性太高了,所以引入了 MethodTimer.Fody 类库,采用编译时注入的方式给方法动态加上Stopwatch 跟踪代码,只需要在目标…...
J2EE征程——第一个纯servletCURD
第一个纯servletCURD 前言在此之前 一,概述二、CURD1介绍2查询并列表显示准备实体类country编写 CountryListServlet配置web.xml为web应用导入mysql-jdbc的jar包 3增加准备增加的页面addc.html编写 CAddServlet配置web.xml测试 4删除修改CountryListServlet…...
BatchOutput PDF for Mac(PDF 批量处理软件)
BatchOutput PDF是一款适用于 Mac 的 PDF 批量处理软件。它可以帮助用户将多个 PDF 文件进行异步处理,提高工作效率。 BatchOutput PDF 可以自动化执行许多任务,包括 PDF 文件的打印、转换、分割、压缩、加密、重命名等,而且它还可以将自定义…...

记一次oracle错误处理
16:00:05 SQL> alter database open; alter database open * 第 1 行出现错误: ORA-01589: 要打开数据库则必须使用 RESETLOGS 或 NORESETLOGS 选项 16:00:49 SQL> startup ORA-01081: 无法启动已在运行的 ORACLE - 请首先关闭它 16:02:56 SQL> shutdown immediate O…...
hugging face下载dataset时候出现You must be authenticated to access it.问题解决
Cannot access gated repo for url https://huggingface.co/tiiuae/falcon-180B/resolve/main/tokenizer_config.json. Repo model tiiuae/falcon-180B is gated. You must be authenticated to access it. 参考https://huggingface.co/docs/huggingface_hub/guides/download …...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...