Python算法——霍夫曼编码树
Python中的霍夫曼编码树
霍夫曼编码是一种用于数据压缩的技术,通过构建霍夫曼编码树(Huffman Tree)来实现。这篇博客将详细讲解霍夫曼编码树的原理、构建方法和使用方式,并提供相应的Python代码实现。
霍夫曼编码原理
霍夫曼编码是一种变长编码,通过给不同的符号分配不同长度的编码,来实现对数据的高效压缩。编码树是一棵二叉树,其中每个叶子节点代表一个符号,而从根到叶子的路径上的每一步都对应一个二进制编码。
霍夫曼编码树的构建过程基于数据中各符号的出现频率,频率越高的符号,其对应的编码路径越短。
霍夫曼编码树的构建
构建霍夫曼编码树的基本步骤如下:
- 创建一个优先队列(最小堆),用于存储各个节点。
- 将每个符号及其频率作为一个节点插入队列中。
- 从队列中选择两个频率最低的节点,合并为一个新节点,其频率为两者之和,然后将新节点插入队列。
- 重复步骤 3,直到队列中只剩下一个节点,即霍夫曼编码树的根节点。
Python代码实现
import heapq
from collections import defaultdictclass HuffmanNode:def __init__(self, symbol, frequency):self.symbol = symbolself.frequency = frequencyself.left = Noneself.right = Nonedef __lt__(self, other):return self.frequency < other.frequencydef build_huffman_tree(data):# 统计每个符号的频率frequency_map = defaultdict(int)for symbol in data:frequency_map[symbol] += 1# 初始化优先队列priority_queue = [HuffmanNode(symbol, frequency) for symbol, frequency in frequency_map.items()]heapq.heapify(priority_queue)# 构建霍夫曼编码树while len(priority_queue) > 1:left_node = heapq.heappop(priority_queue)right_node = heapq.heappop(priority_queue)merged_node = HuffmanNode(None, left_node.frequency + right_node.frequency)merged_node.left, merged_node.right = left_node, right_nodeheapq.heappush(priority_queue, merged_node)return priority_queue[0]def huffman_codes(node, current_code="", code_map=None):if code_map is None:code_map = {}if node is not None:if node.symbol is not None:code_map[node.symbol] = current_codehuffman_codes(node.left, current_code + "0", code_map)huffman_codes(node.right, current_code + "1", code_map)return code_map# 示例
data_to_compress = "hello world"
huffman_tree_root = build_huffman_tree(data_to_compress)
huffman_code_map = huffman_codes(huffman_tree_root)print("Huffman Codes:")
for symbol, code in huffman_code_map.items():print(f"{symbol}: {code}")
示例说明
以上示例中,我们使用字符串 “hello world” 来演示霍夫曼编码的构建过程。在示例中,每个字符都被看作一个符号,并计算其频率。然后,根据频率构建霍夫曼编码树,最终得到每个符号对应的霍夫曼编码。
输出结果:
Huffman Codes:
h: 110
e: 01
o: 111
d: 001
l: 000
r: 10
w: 0011
这表示字符 “h” 对应的霍夫曼编码为 “110”,字符 “e” 对应的编码为 “01”,以此类推。通过理解霍夫曼编码树的构建和编码方式,我们可以在数据压缩中应用这一技术。
相关文章:

Python算法——霍夫曼编码树
Python中的霍夫曼编码树 霍夫曼编码是一种用于数据压缩的技术,通过构建霍夫曼编码树(Huffman Tree)来实现。这篇博客将详细讲解霍夫曼编码树的原理、构建方法和使用方式,并提供相应的Python代码实现。 霍夫曼编码原理 霍夫曼编…...

hql面试题之上海某资深数仓开发工程师面试题-求不连续月份的月平均值
1.题目 A,B两组产品的月平均值,月平均值是当月的前三个月值的一个平均值,注意月份是不连续的,如果当月的前面的月份不存在,则为0。如A组2023-04的月平均值为2023年1月的数据加2023-02月的数据的平均值,因为没有其他月…...
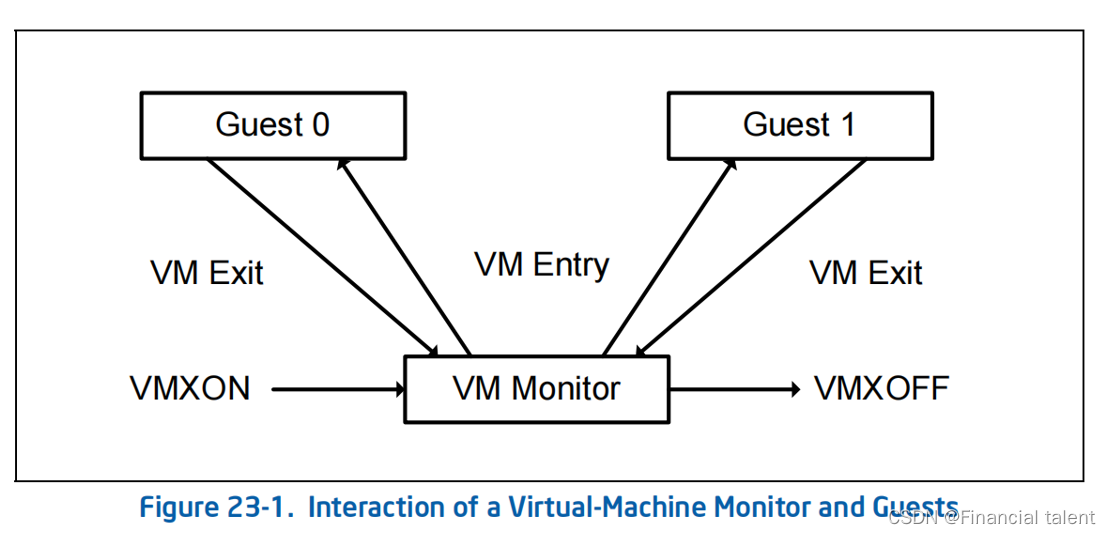
VT驱动开发
VT技术(编写一个VT框架) 1.VT技术介绍 1.技术介绍 1.VT技术 VT技术是Intel提供的虚拟化技术,全称为Intel Virtualization Technology。它是一套硬件和软件的解决方案,旨在增强虚拟化环境的性能、可靠性和安全性。VT技术允许在一台物理计算机上同时运…...

火柴人版王者-Java
主类 package com.sxt; import com.sxt.beast.Beast; import java.awt.Component; import java.awt.Graphics; import java.awt.Image; import java.awt.Toolkit; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.KeyAdapter…...

docker 中的–mount 和-v 参数有啥区别
docker 中的–mount 和-v 参数有啥区别 --mount 和 -v 是 Docker 中用于挂载卷(Volumes)的两种不同的方式。 --mount 参数: 这是一种更为灵活和强大的挂载方式,允许你指定多个选项。 使用 --mount 参数,你可以指定挂…...
设计规则:模块化的力量
这是一本比较冷门的书**《设计规则:模块化的力量》**,虽然豆瓣上只有58个评价,但是确实能学到很多东西。 这本书对我非常深远。不是是投资,创业,还是其他领域,模块化思想都能帮上你。这本书告诉我们生万物…...
)
数据结构与算法之递归: LeetCode 78. 子集 (Typescript版)
子集 https://leetcode.cn/problems/subsets/ 描述 给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。 示例 1 输入:nums [1,2,3]…...
C# 使用 Fody 监控方法执行时间
写在前面 在做性能调优的时候,经常需要跟踪具体方法的执行时间;通过插入Stopwatch的方案对代码的侵入性太高了,所以引入了 MethodTimer.Fody 类库,采用编译时注入的方式给方法动态加上Stopwatch 跟踪代码,只需要在目标…...
J2EE征程——第一个纯servletCURD
第一个纯servletCURD 前言在此之前 一,概述二、CURD1介绍2查询并列表显示准备实体类country编写 CountryListServlet配置web.xml为web应用导入mysql-jdbc的jar包 3增加准备增加的页面addc.html编写 CAddServlet配置web.xml测试 4删除修改CountryListServlet…...
BatchOutput PDF for Mac(PDF 批量处理软件)
BatchOutput PDF是一款适用于 Mac 的 PDF 批量处理软件。它可以帮助用户将多个 PDF 文件进行异步处理,提高工作效率。 BatchOutput PDF 可以自动化执行许多任务,包括 PDF 文件的打印、转换、分割、压缩、加密、重命名等,而且它还可以将自定义…...

记一次oracle错误处理
16:00:05 SQL> alter database open; alter database open * 第 1 行出现错误: ORA-01589: 要打开数据库则必须使用 RESETLOGS 或 NORESETLOGS 选项 16:00:49 SQL> startup ORA-01081: 无法启动已在运行的 ORACLE - 请首先关闭它 16:02:56 SQL> shutdown immediate O…...
hugging face下载dataset时候出现You must be authenticated to access it.问题解决
Cannot access gated repo for url https://huggingface.co/tiiuae/falcon-180B/resolve/main/tokenizer_config.json. Repo model tiiuae/falcon-180B is gated. You must be authenticated to access it. 参考https://huggingface.co/docs/huggingface_hub/guides/download …...
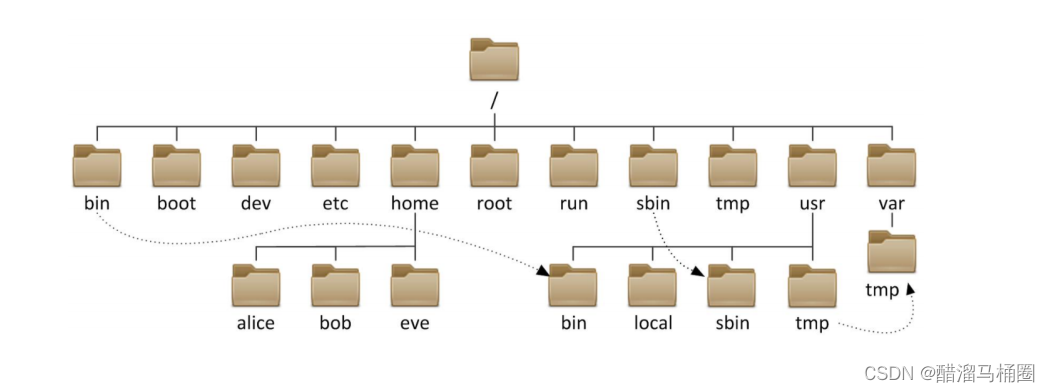
数据结构---树
树概念及结构 1.树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 有一个特殊的结点,…...

tomcat调优配置
一. 设置账户进入管理页面 通过浏览器进入Tomcat7的管理模块页面:http://localhost:8080/manager/status 按照提示,在Tomcat7服务器指定的位置修改配置文件(conf/tomcat-users.xml),增加相应的用户和角色配置标签 <…...
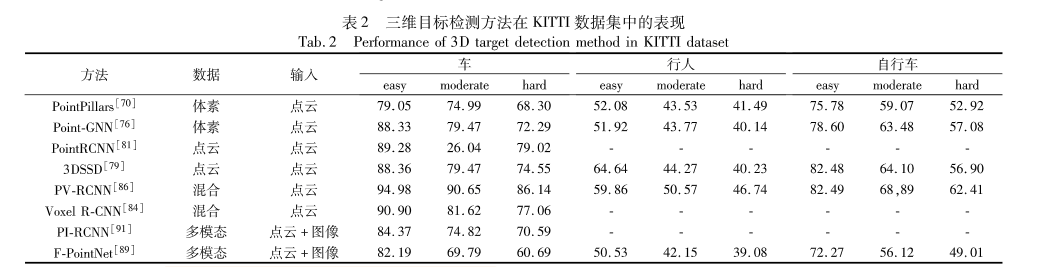
基于深度学习的点云三维目标检测方法综述
论文标题:基于深度学习的点云三维目标检测方法综述 作者:郭毅锋1,2†,吴帝浩1,魏青民1 发表日期: 2023 1 阅读日期 :2023 11 29 研究背景&…...

Linux命令中的符号
目录 1 管道符 | 1.1 | grep [要检索的东西] 1.2 echo | tee 2 重定向 2.1 输出重定向覆盖 > 2.2 输出重定向添加 >> 2.3 文件输入重定向 < 2.4 多行文本输入重定向 << 2.5 常用搭配 2.5.1 终端不显示 > /dev/null 1 管道符 | 我们…...

BTCPay Server:免费、安全、开源的比特币支付处理器 | 开源日报 No.90
MunGell/awesome-for-beginners Stars: 58.0k License: NOASSERTION 这个项目是一个收集开源项目的列表,旨在帮助初学者找到可以贡献代码的机会。该列表按编程语言分类,并列出了每个项目以及其标签 (如 “good-first-issue”、“beginner” 等)。主要功…...

【数据挖掘】国科大刘莹老师数据挖掘课程作业 —— 第三次作业
Written Part 1. 基于表 1 1 1 回答下列问题(min_sup40%, min_conf75%): Transaction IDItems Bought0001{a, d, e}0024{a, b, c, e}0012{a, b, d, e}0031{a, c, d, e}0015{b, c, e}0022{b, d, e}0029{c, d}0040{a, b, c}0033{a, d, e}0038…...

Windows挂载NFS
ubuntu开启nfs 安装 sudo apt install nfs-kernel-server编辑 /etc/exports /data/share *(rw,no_root_squash)重启服务 sudo systemctl restart nfs-server.service验证 showmount -e localhostwindows连接NFS 选择控制面板 > 程序 > 启用或关闭 Windows 功能 添加…...
数据结构第五课 -----二叉树的代码实现
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
